የማትሪክስ ምሳሌዎችን ኢጂንቫሉስ እና ኢጂንቬክተሮችን ያግኙ። የማትሪክስ ባህሪ እኩልታ
ተመሳሳይ የሆኑ የመስመር እኩልታዎች ስርዓት
ተመሳሳይ የሆነ የመስመር እኩልታዎች ስርዓት የቅጹ ስርዓት ነው።
በዚህ ጉዳይ ላይ ግልጽ ነው ![]() , ምክንያቱም በእነዚህ መወሰኛዎች ውስጥ ያሉት የአንዱ አምዶች ሁሉም ንጥረ ነገሮች ከዜሮ ጋር እኩል ናቸው።
, ምክንያቱም በእነዚህ መወሰኛዎች ውስጥ ያሉት የአንዱ አምዶች ሁሉም ንጥረ ነገሮች ከዜሮ ጋር እኩል ናቸው።
ያልታወቁት እንደ ቀመሮቹ ስለሚገኙ ![]() , ከዚያም በጉዳዩ ውስጥ Δ ≠ 0, ስርዓቱ ልዩ የሆነ ዜሮ መፍትሄ አለው x = y = ዝ= 0. ነገር ግን በብዙ ችግሮች ውስጥ አስገራሚው ጥያቄ አንድ ወጥ የሆነ ሥርዓት ከዜሮ ውጪ መፍትሄዎች አሉት የሚለው ነው።
, ከዚያም በጉዳዩ ውስጥ Δ ≠ 0, ስርዓቱ ልዩ የሆነ ዜሮ መፍትሄ አለው x = y = ዝ= 0. ነገር ግን በብዙ ችግሮች ውስጥ አስገራሚው ጥያቄ አንድ ወጥ የሆነ ሥርዓት ከዜሮ ውጪ መፍትሄዎች አሉት የሚለው ነው።
ቲዎረም.
የመስመራዊ ተመሳሳይ እኩልታዎች ስርዓት ዜሮ ያልሆነ መፍትሄ እንዲኖረው Δ ≠ 0 አስፈላጊ እና በቂ ነው።
ስለዚህ, ወሳኙ Δ ≠ 0 ከሆነ, ስርዓቱ ልዩ መፍትሄ አለው. Δ ≠ 0 ከሆነ፣ የመስመራዊ ተመሳሳይ እኩልታዎች ስርዓት ማለቂያ የሌላቸው መፍትሄዎች አሉት።

ምሳሌዎች።
የኢጂንቬክተሮች እና የማትሪክስ እሴቶች  , አንድ ካሬ ማትሪክስ ይሰጥ X - አንዳንድ ማትሪክስ-አምድ ፣ ቁመታቸው ከማትሪክስ ቅደም ተከተል ጋር ይዛመዳል. .
, አንድ ካሬ ማትሪክስ ይሰጥ X - አንዳንድ ማትሪክስ-አምድ ፣ ቁመታቸው ከማትሪክስ ቅደም ተከተል ጋር ይዛመዳል. .
ሀ አንድ ካሬ ማትሪክስ ይሰጥ
በብዙ ችግሮች ውስጥ እኩልታውን ግምት ውስጥ ማስገባት አለብን
λ የተወሰነ ቁጥር ባለበት። ለማንኛውም λ ይህ እኩልታ ዜሮ መፍትሄ እንዳለው ግልጽ ነው. ይህ እኩልታ ዜሮ ያልሆኑ መፍትሄዎች ያለው ቁጥር λ ይባላልኢጂን ዋጋ - አንዳንድ ማትሪክስ-አምድ ፣ ቁመታቸው ከማትሪክስ ቅደም ተከተል ጋር ይዛመዳልማትሪክስ አንድ ካሬ ማትሪክስ ይሰጥ, ኤ ለእንደዚህ አይነት λ ይባላልኢጂን ዋጋ - አንዳንድ ማትሪክስ-አምድ ፣ ቁመታቸው ከማትሪክስ ቅደም ተከተል ጋር ይዛመዳል.
eigenvector - አንዳንድ ማትሪክስ-አምድ ፣ ቁመታቸው ከማትሪክስ ቅደም ተከተል ጋር ይዛመዳልየማትሪክስ ኢጂንቬክተርን እንፈልግ . ምክንያቱም∙ኢ X = X ![]() , ከዚያም የማትሪክስ እኩልታ እንደ እንደገና ሊጻፍ ይችላል
, ከዚያም የማትሪክስ እኩልታ እንደ እንደገና ሊጻፍ ይችላል ![]() ወይም
ወይም  .
.
. በተስፋፋ መልኩ፣ ይህ እኩልታ እንደ የመስመር እኩልታዎች ስርዓት እንደገና ሊፃፍ ይችላል። በእውነት 
እና ስለዚህ ስለዚህ፣ መጋጠሚያዎችን ለመወሰን ተመሳሳይ የሆነ የመስመር እኩልታዎች ስርዓት አግኝተናል, x 1, x 2 x 3 አንድ ካሬ ማትሪክስ ይሰጥቬክተር

. ለአንድ ስርዓት ዜሮ ያልሆኑ መፍትሄዎች እንዲኖሩት አስፈላጊ እና በቂ የስርአቱ ወሳኝ ከዜሮ ጋር እኩል መሆን አለበት, ማለትም. ይህ ለ λ የ3ኛ ዲግሪ እኩልታ ነው። ይባላልኢጂን ዋጋ - አንዳንድ ማትሪክስ-አምድ ፣ ቁመታቸው ከማትሪክስ ቅደም ተከተል ጋር ይዛመዳልየባህሪ እኩልታ
እና የ λ እሴቶችን ለመወሰን ያገለግላል. አንድ ካሬ ማትሪክስ ይሰጥእያንዳንዱ ኢጂንቫልዩ λ ከ eigenvector ጋር ይዛመዳል
ስለዚህ, ወሳኙ Δ ≠ 0 ከሆነ, ስርዓቱ ልዩ መፍትሄ አለው. Δ ≠ 0 ከሆነ፣ የመስመራዊ ተመሳሳይ እኩልታዎች ስርዓት ማለቂያ የሌላቸው መፍትሄዎች አሉት።
, የማን መጋጠሚያዎች ከስርዓቱ የሚወሰኑት በተመጣጣኝ ዋጋ λ.
የተለያዩ የፊዚክስ ቅርንጫፎችን በሚያጠኑበት ጊዜ የቁጥር እሴቶቻቸውን በመጥቀስ ሙሉ በሙሉ የሚወሰኑ መጠኖች አሉ ለምሳሌ ርዝመት, አካባቢ, ክብደት, ሙቀት, ወዘተ. እንደነዚህ ዓይነቶቹ መጠኖች ስካላር ይባላሉ. ነገር ግን, ከነሱ በተጨማሪ, መጠኖችም አሉ, ከቁጥራዊ እሴት በተጨማሪ, በቦታ ውስጥ አቅጣጫቸውን ማወቅ አስፈላጊ ነው, ለምሳሌ በሰውነት ላይ የሚሠራውን ኃይል, ፍጥነት እና ፍጥነት መጨመር. አካል በጠፈር ውስጥ ሲንቀሳቀስ፣ የመግነጢሳዊ መስክ ጥንካሬ በተወሰነ ቦታ ላይ እና ወዘተ. እንደነዚህ ዓይነቶቹ መጠኖች የቬክተር መጠኖች ይባላሉ.
ጥብቅ ፍቺን እናስተዋውቅ.
የተመራው ክፍልከመካከላቸው የትኛው የመጀመሪያው እና ሁለተኛው እንደሆነ ከሚታወቅባቸው ጫፎች አንፃር አንድ ክፍል እንጥራ።

ቬክተርየተወሰነ ርዝመት ያለው የተመራው ክፍል ይባላል፣ ማለትም ይህ የተወሰነ ርዝመት ያለው ክፍል ነው, እሱም ከሚገድበው ነጥብ አንዱ እንደ መጀመሪያው እና ሁለተኛው እንደ መጨረሻው ይወሰዳል. ከሆነ - አንዳንድ ማትሪክስ-አምድ ፣ ቁመታቸው ከማትሪክስ ቅደም ተከተል ጋር ይዛመዳል- የቬክተር መጀመሪያ; ለመጨረሻው ነው, ከዚያም ቬክተር በምልክት ይገለጻል, በተጨማሪም, ቬክተሩ ብዙውን ጊዜ በአንድ ፊደል ይገለጻል. በሥዕሉ ላይ, ቬክተሩ በክፋይ, እና አቅጣጫው በቀስት ይገለጻል.
ሞጁል, ከዚያም የማትሪክስ እኩልታ እንደ እንደገና ሊጻፍ ይችላል ርዝመትአንድ ቬክተር የሚገልጸው የተመራው ክፍል ርዝመት ይባላል. የተገለጸው በ || ወይም ||.
ዜሮ ቬክተር እየተባለ የሚጠራውን፣ መጀመሪያውና መጨረሻው የተገጣጠመውን እንደ ቬክተር እናጨምረዋለን። የተሰየመ ነው። ዜሮ ቬክተር የተወሰነ አቅጣጫ የለውም እና ሞጁሉ ዜሮ ||=0 ነው.
ቬክተሮች ተጠርተዋል ኮላይኔር, እነሱ በተመሳሳይ መስመር ላይ ወይም በትይዩ መስመሮች ላይ ካሉ. ከዚህም በላይ, ቬክተሮች እና በተመሳሳይ አቅጣጫ ከሆኑ, እንጽፋለን, ተቃራኒ.
ከተመሳሳይ አውሮፕላን ጋር ትይዩ በሆኑ ቀጥታ መስመሮች ላይ የሚገኙት ቬክተሮች ተጠርተዋል ኮፕላላር.
ሁለቱ ቬክተሮች ተጠርተዋል እኩል ነው።, እነሱ ኮላይነር ከሆኑ, ተመሳሳይ አቅጣጫ አላቸው እና ርዝመታቸው እኩል ናቸው. በዚህ ጉዳይ ላይ ይጽፋሉ.
ከቬክተር እኩልነት ፍቺ ስንነሳ አንድ ቬክተር ከራሱ ጋር በትይዩ ሊጓጓዝ ይችላል, መነሻውን በማንኛውም ቦታ ላይ ያስቀምጣል.
ለምሳሌ ።
በቬክተሮች ላይ ያሉ ቀጥታ ስራዎች
የቬክተር ምርት እና ቁጥሩ λ አዲስ ቬክተር ነው፡-
የቬክተር እና የቁጥር λ ምርት በ.

ለምሳሌ ልክ እንደ ቬክተር በተመሳሳይ አቅጣጫ የሚመራ እና የቬክተሩን ያህል ግማሽ የሚያክል ርዝመት ያለው ቬክተር አለ።
የተዋወቀው ክዋኔ የሚከተሉትን ባህሪዎች አሉት
ፍቀድ እና ሁለት የዘፈቀደ ቬክተር ይሁኑ። የዘፈቀደ ነጥብ እንውሰድ ኦእና ቬክተር ይገንቡ. ከዚያ በኋላ ከነጥቡ - አንዳንድ ማትሪክስ-አምድ ፣ ቁመታቸው ከማትሪክስ ቅደም ተከተል ጋር ይዛመዳልቬክተሩን ወደ ጎን እናስቀምጠው. የመጀመሪያውን ቬክተር መጀመሪያ ከሁለተኛው ጫፍ ጋር የሚያገናኘው ቬክተር ይባላል መጠንየእነዚህ ቬክተሮች እና የተወከለው ![]() .
.

የተቀመረው የቬክተር መደመር ፍቺ ይባላል parallelogram ደንብ, ተመሳሳይ የቬክተሮች ድምር እንደሚከተለው ሊገኝ ስለሚችል. ከነጥቡ ለሌላ ጊዜ እናዘገይ ኦቬክተሮች እና . በእነዚህ ቬክተሮች ላይ ትይዩአዊ ሎግራም እንገንባ OABC. ከቬክተሮች፣ከዚያም ቬክተር፣ይህም ከቬርቴክስ የተሳለ ትይዩ ሰያፍ ነው። ኦ, በግልጽ የቬክተር ድምር ይሆናል.
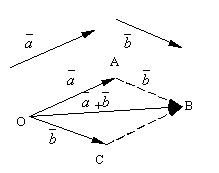
የቬክተር መጨመር የሚከተሉትን ባህሪያት ማረጋገጥ ቀላል ነው.
ለተሰጠው ቬክተር የቬክተር ኮሊኔር, ርዝመቱ እኩል እና በተቃራኒው አቅጣጫ ይባላል ተቃራኒቬክተር ለአንድ ቬክተር እና በ ይገለጻል. ተቃራኒው ቬክተር ቬክተሩን በቁጥር λ = -1: በማባዛት ውጤት ሊቆጠር ይችላል.
በድር ጣቢያ ላይ የሂሳብ ቀመሮችን እንዴት ማስገባት እንደሚቻል?
መቼም አንድ ወይም ሁለት የሂሳብ ቀመሮችን ወደ ድረ-ገጽ ማከል ካስፈለገዎት ይህን ለማድረግ ቀላሉ መንገድ በአንቀጹ ላይ እንደተገለፀው ነው፡ የሂሳብ ቀመሮች በቀላሉ በጣቢያው ላይ በቮልፍራም አልፋ በራስ-ሰር በሚፈጠሩ ስዕሎች መልክ ገብተዋል . ከቀላልነት በተጨማሪ ይህ ሁለንተናዊ ዘዴ በፍለጋ ሞተሮች ውስጥ የጣቢያውን ታይነት ለማሻሻል ይረዳል። ለረጅም ጊዜ እየሰራ ነው (እና, እኔ እንደማስበው, ለዘላለም ይሰራል), ነገር ግን ቀድሞውኑ ከሥነ ምግባር ያለፈ ነው.
በጣቢያዎ ላይ በመደበኛነት የሂሳብ ቀመሮችን የሚጠቀሙ ከሆነ ፣እንግዲህ እመክራለሁ MathJax - ልዩ የጃቫ ስክሪፕት ቤተ-መጽሐፍት በድር አሳሾች ውስጥ MathML ፣ LaTeX ወይም ASCIIMathML ማርከርን በመጠቀም የሂሳብ ምልክቶችን ያሳያል።
MathJaxን መጠቀም ለመጀመር ሁለት መንገዶች አሉ (1) ቀላል ኮድ በመጠቀም የ MathJax ስክሪፕት በፍጥነት ከድር ጣቢያዎ ጋር ማገናኘት ይችላሉ, ይህም ከርቀት አገልጋይ በትክክለኛው ጊዜ ይጫናል (የአገልጋዮች ዝርዝር); (2) የ MathJax ስክሪፕት ከርቀት አገልጋይ ወደ አገልጋይዎ ያውርዱ እና ከሁሉም የጣቢያዎ ገጾች ጋር ያገናኙት። ሁለተኛው ዘዴ - የበለጠ ውስብስብ እና ጊዜ የሚወስድ - የጣቢያዎን ገጾች መጫን ያፋጥናል, እና ወላጅ MathJax አገልጋይ በሆነ ምክንያት ለጊዜው የማይገኝ ከሆነ, ይህ በማንኛውም መንገድ የራስዎን ጣቢያ አይጎዳውም. እነዚህ ጥቅሞች ቢኖሩም, ቀላል, ፈጣን እና ቴክኒካዊ ክህሎቶችን የማይፈልግ ስለሆነ የመጀመሪያውን ዘዴ መርጫለሁ. የእኔን ምሳሌ ተከተሉ እና በ 5 ደቂቃዎች ውስጥ ሁሉንም የ MathJax ባህሪያት በጣቢያዎ ላይ መጠቀም ይችላሉ።
ከዋናው MathJax ድረ-ገጽ ወይም በሰነድ ገፅ ላይ የተወሰዱ ሁለት የኮድ አማራጮችን በመጠቀም MathJax ላይብረሪ ስክሪፕት ከሩቅ አገልጋይ ማገናኘት ይችላሉ።
ከእነዚህ የኮድ አማራጮች ውስጥ አንዱ መቅዳት እና ወደ ድረ-ገጽዎ ኮድ መለጠፍ አለበት፣ በተለይም በመለያዎች መካከል እና ወይም ከመለያው በኋላ ወዲያውኑ። በመጀመሪያው አማራጭ MathJax በፍጥነት ይጭናል እና ገጹን በትንሹ ይቀንሳል። ግን ሁለተኛው አማራጭ የ MathJax የቅርብ ጊዜ ስሪቶችን በራስ-ሰር ይከታተላል እና ይጭናል። የመጀመሪያውን ኮድ ካስገቡ, በየጊዜው መዘመን ያስፈልገዋል. ሁለተኛውን ኮድ ካስገቡ, ገጾቹ በዝግታ ይጫናሉ, ነገር ግን የ MathJax ዝመናዎችን በተከታታይ መከታተል አያስፈልግዎትም.
MathJax ን ለማገናኘት ቀላሉ መንገድ በብሎገር ወይም በዎርድፕረስ ነው፡ በጣቢያ መቆጣጠሪያ ፓኔል ውስጥ የሶስተኛ ወገን ጃቫ ስክሪፕት ኮድ ለማስገባት የተነደፈ መግብርን ያክሉ፣ ከላይ የቀረበውን የማውረጃ ኮድ የመጀመሪያ ወይም ሁለተኛ ቅጂ ይቅዱ እና መግብርን ያቅርቡ። ወደ አብነት መጀመሪያ (በነገራችን ላይ ይህ በጭራሽ አስፈላጊ አይደለም ፣ የ MathJax ስክሪፕት በተመሳሰለ መልኩ ስለተጫነ)። ይኼው ነው። አሁን የMathML፣ LaTeX እና ASCIIMathML ማርክ አገባብ ይማሩ፣ እና የሂሳብ ቀመሮችን በጣቢያዎ ድረ-ገጾች ውስጥ ለማስገባት ዝግጁ ነዎት።
ማንኛውም ፍራክታል የተገነባው በተወሰነ ደንብ መሰረት ነው, እሱም በቋሚነት ያልተገደበ ቁጥር ይተገበራል. እያንዳንዱ እንደዚህ ያለ ጊዜ ድግግሞሽ ይባላል.
Menger ስፖንጅ ለመሥራት የሚደጋገሙ አልጎሪዝም በጣም ቀላል ነው፡ የመጀመሪያው ኪዩብ ከጎን 1 ጋር ከፊቶቹ ጋር ትይዩ በሆኑ አውሮፕላኖች ወደ 27 እኩል ኩብ የተከፈለ ነው። አንድ ማዕከላዊ ኩብ እና 6 ኩብ ከእሱ አጠገብ በፊቶቹ በኩል ይወገዳሉ. ውጤቱም ቀሪዎቹን 20 ትናንሽ ኩቦች ያካተተ ስብስብ ነው. በእያንዳንዱ በእነዚህ ኩቦች ተመሳሳይ ነገር በማድረግ 400 ትናንሽ ኩቦችን ያካተተ ስብስብ እናገኛለን. ይህን ሂደት ያለማቋረጥ በመቀጠል, Menger ስፖንጅ እናገኛለን.
የአንድ ካሬ ማትሪክስ ኢጂንቬክተር በተሰጠው ማትሪክስ ሲባዛ ኮሊንየር ቬክተርን የሚያመጣ ነው። በቀላል ቃላት ፣ ማትሪክስ በ eigenvector ሲባዛ ፣ የኋለኛው ተመሳሳይ ሆኖ ይቆያል ፣ ግን በተወሰነ ቁጥር ተባዝቷል።
ፍቺeigenvector ዜሮ ያልሆነ ቬክተር V ነው፣ እሱም በካሬ ማትሪክስ M ሲባዛ፣ ራሱ በተወሰነ ቁጥር λ ይጨምራል። በአልጀብራ አጻጻፍ የሚከተለውን ይመስላል።
M × V = λ × V፣
የት λ የማትሪክስ M eigenvalue ነው።
የቁጥር ምሳሌን እንመልከት። ለመቅዳት ቀላልነት፣ በማትሪክስ ውስጥ ያሉት ቁጥሮች በሰሚኮሎን ይለያያሉ። ማትሪክስ ይኑረን፡-
- M = 0; 4;
- 6; 10.
በአምድ ቬክተር እናባዛው፡-
- ቪ = -2;
ማትሪክስ በአምድ ቬክተር ስናባዛው ደግሞ የአምድ ቬክተር እናገኛለን። በጥብቅ የሒሳብ ቋንቋ 2 × 2 ማትሪክስ በአምድ ቬክተር የማባዛት ቀመር ይህን ይመስላል።
- M × V = M11 × V11 + M12 × V21;
- M21 × V11 + M22 × V21.
M11 ማለት በመጀመሪያው ረድፍ እና በመጀመሪያው አምድ ውስጥ የሚገኘው የማትሪክስ M አባል ሲሆን M22 ማለት ደግሞ በሁለተኛው ረድፍ እና በሁለተኛው ረድፍ ውስጥ የሚገኝ አካል ማለት ነው. ለኛ ማትሪክስ እነዚህ ንጥረ ነገሮች ከ M11 = 0, M12 = 4, M21 = 6, M22 10 ጋር እኩል ናቸው. ለአንድ አምድ ቬክተር, እነዚህ እሴቶች ከ V11 = -2, V21 = 1 ጋር እኩል ናቸው. በዚህ ቀመር መሠረት. የሚከተለውን የካሬ ማትሪክስ ውጤት በቬክተር እናገኛለን።
- M × V = 0 × (-2) + (4) × (1) = 4;
- 6 × (-2) + 10 × (1) = -2.
ለመመቻቸት የዓምድ ቬክተርን በአንድ ረድፍ እንፃፍ። ስለዚህ, ካሬውን ማትሪክስ በቬክተር (-2; 1) እናባዛለን, በዚህም ምክንያት ቬክተር (4; -2). በግልጽ ለማየት እንደሚቻለው, ይህ ተመሳሳይ ቬክተር በ λ = -2 ተባዝቷል. Lambda በዚህ ጉዳይ ላይ የማትሪክስ ኢጂን ዋጋን ያመለክታል.
የማትሪክስ ኢጂንቬክተር ኮላይኔር ቬክተር ነው፣ ማለትም፣ በማትሪክስ ሲባዛ ቦታውን በህዋ ላይ የማይለውጥ ነገር ነው። በቬክተር አልጀብራ ውስጥ ያለው የኮላይኔሪቲ ጽንሰ-ሀሳብ በጂኦሜትሪ ውስጥ ካለው ትይዩነት ቃል ጋር ተመሳሳይ ነው። በጂኦሜትሪክ አተረጓጎም, ኮላይኔር ቬክተሮች የተለያየ ርዝመት ያላቸው ትይዩ የተመሩ ክፍሎች ናቸው. ከዩክሊድ ዘመን ጀምሮ፣ አንድ መስመር ከሱ ጋር ትይዩ የሆኑ ማለቂያ የሌላቸው መስመሮች እንዳሉት እናውቃለን፣ ስለዚህ እያንዳንዱ ማትሪክስ ማለቂያ የሌለው የኢጂንቬክተሮች ብዛት አለው ብሎ ማሰብ ምክንያታዊ ነው።
ካለፈው ምሳሌ ግልጽ የሆነው ኢጂንቬክተሮች (-8; 4) እና (16; -8) እና (32, -16) ሊሆኑ ይችላሉ. እነዚህ ሁሉ ከ eigenvalue λ = -2 ጋር የሚዛመዱ ኮላይኔር ቬክተሮች ናቸው። ዋናውን ማትሪክስ በእነዚህ ቬክተሮች ስናባዛው አሁንም ከዋናው በ2 ጊዜ የሚለይ ቬክተር ይዘን እንጨርሳለን። ለዚህም ነው ኢጂንቬክተርን የማግኘት ችግሮችን በሚፈታበት ጊዜ, በመስመር ላይ ገለልተኛ የሆኑ የቬክተር እቃዎችን ብቻ ማግኘት አስፈላጊ ነው. ብዙ ጊዜ፣ ለ n × n ማትሪክስ፣ n የ eigenvectors ብዛት አለ። የእኛ ካልኩሌተር ሁለተኛ ደረጃ ካሬ ማትሪክስ ለመተንተን የተነደፈ ነው, ስለዚህ ሁልጊዜ ማለት ይቻላል ውጤቱ ሁለት eigenvectors ታገኛላችሁ, ከተጋጠሙትም ሁኔታዎች በስተቀር.
ከላይ ባለው ምሳሌ የዋናውን ማትሪክስ ኢጂንቬክተር አስቀድመን አውቀናል እና የላምዳ ቁጥርን በግልፅ ወስነናል። ሆኖም ግን, በተግባር, ሁሉም ነገር በተቃራኒው ይከናወናል-የኢጂነን እሴቶቹ መጀመሪያ ላይ እና ከዚያ በኋላ ብቻ ናቸው.
የመፍትሄው ስልተ ቀመርየመጀመሪያውን ማትሪክስ M እንደገና እንመልከተው እና ሁለቱንም ኢጂንቬክተሮች ለማግኘት እንሞክር። ስለዚህ ማትሪክስ የሚከተለው ይመስላል-
- M = 0; 4;
- 6; 10.
በመጀመሪያ የሚከተለውን ማትሪክስ ወሳኙን ማስላት የሚጠይቀውን eigenvalue λ መወሰን አለብን።
- (0 - λ); 4;
- 6; (10 - λ).
ይህ ማትሪክስ የሚገኘው የማይታወቅ λን ከዋናው ዲያግናል ላይ ካሉ ንጥረ ነገሮች በመቀነስ ነው። የሚወስነው መደበኛውን ቀመር በመጠቀም ነው፡-
- detA = M11 × M21 - M12 × M22
- detA = (0 - λ) × (10 - λ) - 24
የእኛ ቬክተር ዜሮ ያልሆነ መሆን ስላለበት፣ የተገኘውን እኩልታ እንደ መስመራዊ ጥገኛ እንቀበላለን እና የእኛን ወሳኙ detA ከዜሮ ጋር እናመሳሰለው።
(0 - λ) × (10 - λ) - 24 = 0
ቅንፎችን እንክፈትና የማትሪክስ የባህሪ እኩልታ እናገኛለን፡-
λ 2 - 10λ - 24 = 0
ይህ አድሎአዊ በመጠቀም መፈታት ያለበት መደበኛ ኳድራቲክ እኩልታ ነው።
D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196
የአድሎአዊው ሥር sqrt (D) = 14 ነው, ስለዚህ λ1 = -2, λ2 = 12. አሁን ለእያንዳንዱ ላምዳ እሴት ኢጂንቬክተሩን መፈለግ አለብን. ለ λ = -2 የስርዓት ቅንጅቶችን እንገልፃለን.
- M - λ × E = 2; 4;
- 6; 12.
በዚህ ቀመር ኢ የማንነት ማትሪክስ ነው። በውጤቱ ማትሪክስ ላይ በመመስረት ፣ የመስመሮች እኩልታዎች ስርዓት እንፈጥራለን-
2x + 4y = 6x + 12y፣
x እና y የኢጂንቬክተር ንጥረ ነገሮች ሲሆኑ።
ሁሉንም X በስተግራ እና ሁሉንም Y በስተቀኝ እንሰበስብ። በግልጽ - 4x = 8y. አገላለጹን በ - 4 ይከፋፍሉት እና x = -2y ያግኙ። አሁን የማንኛውንም የማይታወቁ እሴቶችን በመውሰድ የማትሪክስ የመጀመሪያውን eigenvector መወሰን እንችላለን (የመስመራዊ ጥገኛ ኢጂንቬክተሮች ወሰን አልባነት ያስታውሱ)። y = 1፣ በመቀጠል x = –2 እንውሰድ። ስለዚህ, የመጀመሪያው eigenvector V1 = (-2; 1) ይመስላል. ወደ መጣጥፉ መጀመሪያ ተመለስ። የኢጂንቬክተር ጽንሰ-ሀሳብን ለማሳየት ማትሪክስን ያባዛነው ይህ የቬክተር ነገር ነው።
አሁን eigenvector ለ λ = 12 እንፈልግ።
- M - λ × E = -12; 4
- 6; -2.
የመስመር እኩልታዎች ተመሳሳይ ስርዓት እንፍጠር;
- -12x + 4y = 6x - 2y
- -18x = -6ይ
- 3x = y.
አሁን x = 1 ን እንወስዳለን, ስለዚህ y = 3. ስለዚህ, ሁለተኛው eigenvector V2 = (1; 3) ይመስላል. ዋናውን ማትሪክስ በተሰጠው ቬክተር ሲያባዙ ውጤቱ ሁልጊዜ በ 12 ሲባዛ አንድ አይነት ቬክተር ይሆናል። አሁን የማትሪክስ ኢጂንቬክተርን እራስዎ እንዴት እንደሚወስኑ ያውቃሉ።
- የሚወስን;
- ፈለግ ፣ ማለትም ፣ በዋናው ዲያግናል ላይ ያሉት ንጥረ ነገሮች ድምር;
- ደረጃ፣ ማለትም፣ ከፍተኛው በመስመር ገለልተኛ የረድፎች/አምዶች ብዛት።
መርሃግብሩ ከላይ በተጠቀሰው ስልተ-ቀመር መሰረት ይሰራል, በተቻለ መጠን የመፍትሄ ሂደቱን ያሳጥራል. በፕሮግራሙ ውስጥ ላምዳ በ "ሐ" ፊደል እንደተሰየመ ማመላከት አስፈላጊ ነው. የቁጥር ምሳሌን እንመልከት።
ፕሮግራሙ እንዴት እንደሚሰራ የሚያሳይ ምሳሌለሚከተለው ማትሪክስ ኢጂንቬክተሮችን ለመወሰን እንሞክር፡-
- M = 5; 13;
- 4; 14.
እነዚህን እሴቶች ወደ ካልኩሌተሩ ህዋሶች እናስገባና መልሱን በሚከተለው መልክ እናገኝ።
- ማትሪክስ ደረጃ፡ 2;
- ማትሪክስ መወሰኛ: 18;
- ማትሪክስ ዱካ: 19;
- የ eigenvector ስሌት: c 2 - 19.00c + 18.00 (የባህሪ እኩልነት);
- Eigenvector ስሌት: 18 (የመጀመሪያው ላምዳ ዋጋ);
- የኢጅንቬክተር ስሌት: 1 (ሁለተኛ ላምዳ ዋጋ);
- የእኩልታዎች ስርዓት ለቬክተር 1: -13x1 + 13y1 = 4x1 - 4y1;
- ለቬክተር 2 የእኩልታዎች ስርዓት: 4x1 + 13y1 = 4x1 + 13y1;
- ኢጅንቬክተር 1: (1; 1);
- ኢጅንቬክተር 2፡ (-3.25፤ 1)።
ስለዚህም ሁለት ቀጥተኛ ገለልተኛ ኢጂንቬክተሮች አግኝተናል።
ማጠቃለያሊኒያር አልጀብራ እና የትንታኔ ጂኦሜትሪ ለማንኛውም የፍሬሽማን ኢንጂነሪንግ ዋና ዋና ትምህርቶች ናቸው። ብዙ ቁጥር ያላቸው ቬክተሮች እና ማትሪክስ በጣም አስፈሪ ናቸው, እና እንደዚህ ባሉ አስቸጋሪ ስሌቶች ውስጥ ስህተቶችን ማድረግ ቀላል ነው. የእኛ ፕሮግራም ተማሪዎች ስሌቶቻቸውን እንዲፈትሹ ወይም ኢጂንቬክተር የማግኘት ችግርን በራስ-ሰር እንዲፈቱ ያስችላቸዋል። በእኛ ካታሎግ ውስጥ ሌሎች የመስመር ላይ አልጀብራ አስሊዎች አሉ፤ በጥናትዎ ወይም በስራዎ ውስጥ ይጠቀሙባቸው።
በማትሪክስ A, ቁጥር ካለ l እንደ AX = lX.
በዚህ ሁኔታ, ቁጥሩ l ከቬክተር X ጋር የሚዛመደው የኦፕሬተር (ማትሪክስ A) ኢጂንቫል ይባላል.
በሌላ አገላለጽ፣ eigenvector ቬክተር ነው፣ በመስመራዊ ኦፕሬተር ተግባር ስር፣ ወደ ኮላይኔር ቬክተርነት የሚቀየር፣ ማለትም። በተወሰነ ቁጥር ብቻ ማባዛት። በአንጻሩ ግን አግባብ ያልሆኑ ቬክተሮች ለመለወጥ በጣም የተወሳሰቡ ናቸው።
ኢጅንቬክተርን (eigenvector) ፍቺን በሥርዓተ ቀመር መልክ እንጻፍ፡-
ሁሉንም ውሎች ወደ ግራ በኩል እናንቀሳቅስ።

የኋለኛው ስርዓት በማትሪክስ መልክ እንደሚከተለው ሊፃፍ ይችላል-
(A - le) X = O
የውጤቱ ስርዓት ሁልጊዜ ዜሮ መፍትሄ አለው X = O. ሁሉም ነፃ ቃላት ከዜሮ ጋር እኩል የሆኑባቸው እንዲህ ያሉ ስርዓቶች ተመሳሳይነት ይባላሉ. የእንደዚህ አይነት ስርዓት ማትሪክስ ካሬ ከሆነ እና መለያው ከዜሮ ጋር እኩል ካልሆነ ፣ ከዚያ የ Cramer ቀመሮችን በመጠቀም ሁል ጊዜ ልዩ መፍትሄ እናገኛለን - ዜሮ። የዚህ ማትሪክስ መወሰኛ ከዜሮ ጋር እኩል ከሆነ እና ብቻ ከሆነ ስርዓቱ ዜሮ ያልሆኑ መፍትሄዎች እንዳለው ማረጋገጥ ይቻላል ፣ ማለትም።
|A - le| =  = 0
= 0
ይህ ከማይታወቅ l ጋር የማትሪክስ ኤ (መስመራዊ ኦፕሬተር) የባህሪ እኩልታ (ባህሪ ፖሊኖሚል) ይባላል።
የመስመራዊ ኦፕሬተር ባህርይ ፖሊኖሚል በመሠረት ምርጫ ላይ የተመካ አለመሆኑን ማረጋገጥ ይቻላል.
ለምሳሌ፣ በማትሪክስ A = የተገለጹትን የመስመራዊ ኦፕሬተር ኢጂንቫሉስ እና ኢጂንቬክተሮችን እንፈልግ።
ይህንን ለማድረግ፣ የባህሪ እኩልታ |A - le| እንፍጠር = ![]() = (1 - ሊ) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; መ = 4 + 140 = 144; eigenvalues l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12)/2 = 7.
= (1 - ሊ) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; መ = 4 + 140 = 144; eigenvalues l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12)/2 = 7.
ኢጂንቬክተሮችን ለማግኘት, ሁለት የእኩልታ ስርዓቶችን እንፈታለን
(A + 5E)X = O
(A - 7E)X = O
ለመጀመሪያዎቹ, የተስፋፋው ማትሪክስ ቅጹን ይወስዳል
![]() ,
,
ከየት ነው x 2 = c, x 1 + (2/3) c = 0; x 1 = -(2/3) ሰ፣ ማለትም እ.ኤ.አ. X (1) = (-(2/3) ሰ; ሰ)
ለሁለተኛዎቹ, የተስፋፋው ማትሪክስ ቅጹን ይወስዳል
![]() ,
,
ከየት x 2 = c 1, x 1 - (2/3) c 1 = 0; x 1 = (2/3) ሰ 1፣ i.e. X (2) = ((2/3) ሰ 1፤ ሰ 1)።
ስለዚህ የዚህ መስመራዊ ኦፕሬተር ኢጂንቬክተሮች ሁሉም የቅርጽ ((2/3) с; ሰ) ከ eigenvalue (-5) እና ከቅጹ ((2/3) с 1፤ с 1) ጋር ያሉ ሁሉም ቬክተሮች ናቸው። eigenvalue 7 .
የኦፕሬተሩ ኤ ማትሪክስ ኢጂንቬክተሮችን ባቀፈ መሠረት ሰያፍ እና ቅርፅ ያለው መሆኑን ማረጋገጥ ይቻላል-
 ,
,
እኔ የዚህ ማትሪክስ ኢጂን እሴቶች በሆንኩበት።
ንግግሩም እውነት ነው፡ ማትሪክስ A በተወሰነ መሰረት ሰያፍ ከሆነ፣ ሁሉም የዚህ መሰረት ቬክተሮች የዚህ ማትሪክስ ኢጂንቬክተሮች ይሆናሉ።
እንዲሁም ሊኒየር ኦፕሬተር n ጥንድ የተለያዩ ኢጂንቫሉስ ካለው፣ ተጓዳኝ ኢጂንቬክተሮች በመስመራዊ ገለልተኛ መሆናቸውን እና የዚህ ኦፕሬተር ማትሪክስ በተዛማጅ መሠረት ሰያፍ ቅርፅ እንዳለው ማረጋገጥ ይቻላል።
ይህንን ባለፈው ምሳሌ እናሳይ። የዘፈቀደ ዜሮ ያልሆኑ እሴቶችን c እና c 1ን እንውሰድ፣ ነገር ግን ቬክተሮች X (1) እና X (2) በመስመር ላይ ገለልተኛ ናቸው፣ ማለትም። መሠረት ይፈጥር ነበር። ለምሳሌ፣ c = c 1 = 3፣ ከዚያም X (1) = (-2; 3)፣ X (2) = (2; 3) እናድርግ።
የእነዚህን ቬክተሮች ቀጥተኛ ነፃነት እናረጋግጥ፡-
12 ≠ 0. በዚህ አዲስ መሠረት, ማትሪክስ A ቅጽ A * = ይወስዳል.
ይህንን ለማረጋገጥ ፎርሙላውን A * = C -1 AC እንጠቀም። መጀመሪያ C -1ን እንፈልግ።
ሐ -1 = ![]() ;
;

የ n ተለዋዋጮች አራት ማዕዘን ቅርፅ f(x 1፣ x 2፣ x n) ድምር ነው፣ እያንዳንዱ ቃል ወይ ከተለዋዋጮች የአንዱ ካሬ፣ ወይም የሁለት የተለያዩ ተለዋዋጮች ውጤት፣ ከተወሰነ ጥምርታ ጋር የተወሰደ፡ f( x 1፣ x 2፣ x n) = ![]() (a ij = a ji)
(a ij = a ji)
ከእነዚህ ጥምርታዎች ያቀፈው ማትሪክስ የኳድራቲክ ቅርጽ ማትሪክስ ይባላል። ይህ ሁልጊዜ የተመጣጠነ ማትሪክስ ነው (ማለትም ስለ ዋናው ዲያግናል ያለው ማትሪክስ ሲሜትሪክ፣ ij = a ji)።
በማትሪክስ ማስታወሻ ውስጥ, አራት ማዕዘን ቅርፅ f (X) = X T AX, የት ነው
በእርግጥም

ለምሳሌ፣ ኳድራቲክ ፎርሙን በማትሪክስ መልክ እንፃፍ።
ይህንን ለማድረግ, የኳድራቲክ ቅርጽ ማትሪክስ እናገኛለን. የእሱ ሰያፍ አካላት ከካሬው ተለዋዋጮች ጋር እኩል ናቸው ፣ እና የተቀሩት ንጥረ ነገሮች የኳድራቲክ ቅርፅ ከተዛማጅ ግማሾች ጋር እኩል ናቸው። ለዛ ነው

የተለዋዋጮች ማትሪክስ-አምድ ማትሪክስ-አምድ ዋይ ባልተዳከመ የመስመር ለውጥ ይገኝ፣ i.e. X = CY፣ ሐ ነጠላ ያልሆነ የ nth ቅደም ተከተል ማትሪክስ ነው። ከዚያም አራት ማዕዘን ቅርፅ f (X) = X T AX = (CY) T A (CY) = (Y T C T) A (CY) = Y T (C T AC) Y.
ስለዚህ፣ ባልተበላሸ መስመራዊ ለውጥ C፣ የኳድራቲክ ቅርጽ ማትሪክስ ቅጹን ይወስዳል፡ A * = C T AC።
ለምሳሌ፣ ከኳድራቲክ ቅጽ f(x 1፣ x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 በመስመራዊ ለውጥ የተገኘውን አራት ማዕዘን ቅርፅ f(y 1፣y 2) እናገኝ።

አራት ማዕዘን ቅርጽ ያለው ፎርም ቀኖናዊ (ቀኖናዊ ቅርጽ አለው) ይባላል ሁሉም ድምጾቹ a ij = 0 ለ i ≠ j, i.e.
ረ(x 1፣ x 2፣ x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =።
የእሱ ማትሪክስ ሰያፍ ነው.
ቲዎረም (ማስረጃ እዚህ አልተሰጠም). ማንኛውም ባለአራት ቅርጽ ያልተበላሸ የመስመር ለውጥን በመጠቀም ወደ ቀኖናዊ ቅርጽ ሊቀንስ ይችላል።
ለምሳሌ፣ አራት ማዕዘን ቅርጾችን ወደ ቀኖናዊ ቅርጽ እንቀንስ
ረ(x 1፣ x 2፣ x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3።
ይህንን ለማድረግ በመጀመሪያ ከተለዋዋጭ x 1 ጋር የተሟላ ካሬ ይምረጡ።
ረ (x 1, x 2, x 3) = 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 2 - x 2 x 3 = 2 (x 1 + x 2) 2 - 5x 2 2 - x 2 x 3።
አሁን ከተለዋዋጭ x 2 ጋር የተሟላ ካሬ እንመርጣለን፡
ረ (x 1, x 2, x 3) = 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2* x 2 * (1/10) x 3 + (1/100) x 3 2) + (5/100) x 3 2 =
= 2(x 1 + x 2) 2 - 5(x 2 - (1/10) x 3) 2 + (1/20) x 3 2።
ከዚያም ያልተበላሸ መስመራዊ ለውጥ y 1 = x 1 + x 2, y 2 = x 2 + (1/10) x 3 እና y 3 = x 3 ይህንን አራት ማዕዘን ቅርጽ ወደ ቀኖናዊው ቅጽ f (y 1, y 2) ያመጣል. , y 3) = 2ይ 1 2 - 5y 2 2 + (1/20) y 3 2 .
የኳድራቲክ ቅርጽ ቀኖናዊ ቅርፅ የሚወሰነው አሻሚ መሆኑን ልብ ይበሉ (ተመሳሳይ አራት ማዕዘን ቅርፅ በተለያየ መንገድ ወደ ቀኖናዊ ቅርጽ ሊቀንስ ይችላል). ይሁን እንጂ በተለያዩ ዘዴዎች የተገኙ ቀኖናዊ ቅርጾች በርካታ የተለመዱ ባህሪያት አሏቸው. በተለይም የኳድራቲክ ቅርፅ አወንታዊ (አሉታዊ) ድምጾች ያላቸው የቃላቶች ብዛት ቅጹን ወደዚህ ቅጽ በመቀነስ ዘዴ ላይ የተመካ አይደለም (ለምሳሌ ፣ በምሳሌው ውስጥ ሁል ጊዜ ሁለት አሉታዊ እና አንድ አዎንታዊ ቅንጅት ይኖራሉ)። ይህ ንብረት የኳድራቲክ ቅርፆች የማይነቃነቅ ህግ ይባላል።
ተመሳሳዩን ኳድራቲክ ቅርፅ ወደ ቀኖናዊ ቅርጽ በተለየ መንገድ በማምጣት ይህንን እናረጋግጥ። ለውጡን በተለዋዋጭ x 2 እንጀምር፡-
ረ (x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3 (x 2 2 +
+ 2* x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3(1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
= -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 = f (y 1 ፣ y 2 ፣ y 3) = -3ይ 1 2 -
+3ይ 2 2 + 2ይ 3 2፣ የት y 1 = - (2/3) x 1 + x 2 + (1/6) x 3፣ y 2 = (2/3) x 1 + (1/6) x 3 እና y 3 = x 1. እዚህ ላይ አሉታዊ ኮፊሸን -3 በ y 1 እና ሁለት አወንታዊ ኮፊሸን 3 እና 2 በ y 2 እና y 3 (ሌላ ዘዴን በመጠቀም በ y 2 ላይ አሉታዊ ኮፊሸን አገኘን (-5) እና ሁለት አዎንታዊ ናቸው፡ 2 እና y 1 እና 1/20 በ y 3)።
በተጨማሪም አራት ማዕዘን ቅርጽ ያለው ማትሪክስ ደረጃ, የኳድራቲክ ቅርጽ ደረጃ ተብሎ የሚጠራው, ከቀኖናዊው ቅርጽ ዜሮ ያልሆኑ ዜሮዎች ቁጥር ጋር እኩል እንደሆነ እና በመስመራዊ ለውጦች ውስጥ እንደማይለወጥ ልብ ሊባል ይገባል.
አራት ማዕዘን ቅርፅ f (X) አወንታዊ (አሉታዊ) ተብሎ ይጠራል ፣ ለሁሉም የተለዋዋጮች እሴቶች በተመሳሳይ ጊዜ ከዜሮ ጋር እኩል ካልሆኑ ፣ እሱ አዎንታዊ ነው ፣ ማለትም። f(X) > 0 (አሉታዊ፣ i.e.
ረ(ኤክስ)< 0).
ለምሳሌ፣ አራት ማዕዘን ቅርፅ f 1 (X) = x 1 2 + x 2 2 አወንታዊ ነው፣ ምክንያቱም የካሬዎች ድምር ነው፣ እና አራት ማዕዘን ቅርፅ f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 አሉታዊ የተወሰነ ነው፣ ምክንያቱም ይወክላል እንደ f 2 (X) = -(x 1 - x 2) 2 ሊወከል ይችላል።
በአብዛኛዎቹ ተግባራዊ ሁኔታዎች ፣ የኳድራቲክ ቅርፅን ትክክለኛ ምልክት ማቋቋም በተወሰነ ደረጃ ከባድ ነው ፣ ስለሆነም ለዚህ ከሚከተሉት ጽንሰ-ሀሳቦች ውስጥ አንዱን እንጠቀማለን (ያለ ማረጋገጫ እንፈጥራቸዋለን)።
ቲዎረም. ሁሉም የማትሪክስ እሴቶች አወንታዊ (አሉታዊ) ከሆኑ ብቻ አራት ማዕዘን ቅርፅ ያለው አወንታዊ (አሉታዊ) ነው።
ቲዎረም (የሲልቬስተር መስፈርት). ሁሉም የዚህ ቅጽ ማትሪክስ ዋና ዋና ታዳጊዎች አዎንታዊ ከሆኑ ብቻ አራት ማዕዘን ቅርፅ ያለው አወንታዊ ነው።
የ nth ማትሪክስ ማትሪክስ የ kth ቅደም ተከተል ዋናው (አንግል) አናሳ የማትሪክስ መወሰኛ ነው፣ የማትሪክስ A () የመጀመሪያ k ረድፎች እና አምዶች።
ለአሉታዊ ኳድራቲክ ቅርጾች የዋናዎቹ ለአካለ መጠን ያልደረሱ ልጆች ምልክቶች ይለዋወጣሉ እና የመጀመሪያ ደረጃ ትንሽ ልጅ አሉታዊ መሆን እንዳለበት ልብ ይበሉ።
ለምሳሌ፡ ለምልክት እርግጠኝነት አራት ማዕዘን ቅርፅ f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 እንመርምር።
![]() = (2 - ሊ)*
= (2 - ሊ)*
* (3 - ሊ) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17; ![]() . ስለዚህ, አራት ማዕዘን ቅርፅ አዎንታዊ ነው.
. ስለዚህ, አራት ማዕዘን ቅርፅ አዎንታዊ ነው.
ዘዴ 2. የማትሪክስ የመጀመሪያ ቅደም ተከተል ርእሰ መምህሩ A D 1 = a 11 = 2> 0. የሁለተኛው ቅደም ተከተል ዋና አካል D 2 = 6 - 4 = 2> 0. ስለዚህ በሲልቬስተር መስፈርት መሰረት አራት ማዕዘን ቅርፅ ያለው ቅርጽ ነው. አዎንታዊ የተወሰነ.
ለምልክት ትክክለኛነት ሌላ አራት ማዕዘን ቅርፅን እንመረምራለን ፣ f(x 1 ፣ x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2።
ዘዴ 1. የኳድራቲክ ቅርጽ A = ማትሪክስ እንገንባ. የባህሪው እኩልነት ቅጹ ይኖረዋል ![]() = (-2 - ሊ)*
= (-2 - ሊ)*
* (-3 - ሊ) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17; ![]() . ስለዚህ, አራት ማዕዘን ቅርፅ አሉታዊ ነው.
. ስለዚህ, አራት ማዕዘን ቅርፅ አሉታዊ ነው.
ዘዴ 2. የማትሪክስ የመጀመሪያ ቅደም ተከተል ዋና ትንሽ A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. በዚህም ምክንያት, በሲልቬስተር መስፈርት መሰረት, አራት ማዕዘን ቅርፅ አሉታዊ ነው (የዋነኞቹ ታዳጊዎች ምልክቶች በመቀነስ ይለዋወጣሉ).
እና እንደ ሌላ ምሳሌ፣ በምልክት የተወሰነውን አራት ማዕዘን ቅርጽ f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 እንመረምራለን.
ዘዴ 1. የኳድራቲክ ቅርጽ A = ማትሪክስ እንገንባ. የባህሪው እኩልነት ቅጹ ይኖረዋል ![]() = (2 - ሊ)*
= (2 - ሊ)*
* (-3 - ሊ) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41; ![]() .
.
ከእነዚህ ቁጥሮች ውስጥ አንዱ አሉታዊ ሲሆን ሌላኛው ደግሞ አዎንታዊ ነው. የ eigenvalues ምልክቶች የተለያዩ ናቸው። ስለዚህ፣ አራት ማዕዘን ቅርፅ በአሉታዊም ሆነ በአዎንታዊ መልኩ የተወሰነ ሊሆን አይችልም፣ ማለትም ይህ አራት ማዕዘን ቅርጽ በምልክት የተወሰነ አይደለም (የማንኛውም ምልክት እሴቶችን ሊወስድ ይችላል)።
ዘዴ 2. የማትሪክስ የመጀመሪያ ቅደም ተከተል ርእሰ መምህሩ A D 1 = a 11 = 2> 0. የሁለተኛው ቅደም ተከተል ዋና ትንሽ D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).
