የመጀመሪያው እና ሁለተኛው አስደናቂ ገደቦች የመፍትሄ ምሳሌዎች ናቸው. አስደናቂ ገደቦች፡ የመጀመሪያ እና ሁለተኛ አስደናቂ ገደቦች
የሁለተኛው አስደናቂ ገደብ ቀመር ሊም x → ∞ 1 + 1 x x = e ነው። ሌላው የአጻጻፍ ስልት ይህን ይመስላል፡ lim x → 0 (1 + x) 1 x = e.
ስለ ሁለተኛው አስደናቂ ገደብ ስንነጋገር፣ ስለ ቅጽ 1 ∞ እርግጠኛ አለመሆንን መቋቋም አለብን፣ ማለትም. አንድነት ወሰን በሌለው ደረጃ።
Yandex.RTB R-A-339285-1
ሁለተኛውን አስደናቂ ገደብ የማስላት ችሎታ ጠቃሚ የሚሆኑባቸውን ችግሮች እናስብ።
ምሳሌ 1
ገደብ ሊም x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 ያግኙ።
መፍትሄ
አስፈላጊውን ቀመር እንተካ እና ስሌቶችን እናከናውን.
ሊም x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 - 2 ∞ 2 + 1 ∞ 2 + 1 4 = 1 - 0 ∞ = 1 ∞
መልሳችን ላልተወሰነ ኃይል አንድ ሆነ። የመፍትሄውን ዘዴ ለመወሰን, እርግጠኛ ያልሆነውን ሰንጠረዥ እንጠቀማለን. ሁለተኛውን አስደናቂ ገደብ እንመርጥ እና ተለዋዋጮችን እንቀይር።
t = - x 2 + 1 2 ⇔ x 2 + 1 4 = - t 2
x → ∞ ከሆነ፣ ከዚያ t → - ∞።
ከተተካው በኋላ ያገኘነውን እንመልከት፡-
ሊም x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 ∞ = ሊም x → ∞ 1 + 1 t - 1 2 t = lim t → ∞ 1 + 1 t t - 1 2 = e - 1 2
መልስ፡-ሊም x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = e - 1 2 .
ምሳሌ 2
ገደብ ሊም x → ∞ x - 1 x + 1 x አስላ።
መፍትሄ
ፍጻሜ የሌለውን ተክተን የሚከተለውን አግኝ።
ሊም x → ∞ x - 1 x + 1 x = ሊም x → ∞ 1 - 1 x 1 + 1 x x = 1 - 0 1 + 0 ∞ = 1 ∞
በመልሱ ውስጥ, እንደ ቀድሞው ችግር እንደገና አንድ አይነት ነገር አግኝተናል, ስለዚህ, ሁለተኛውን አስደናቂ ገደብ እንደገና መጠቀም እንችላለን. በመቀጠል በኃይል ተግባሩ መሠረት ሙሉውን ክፍል መምረጥ አለብን-
x - 1 x + 1 = x + 1 - 2 x + 1 = x + 1 x + 1 - 2 x + 1 = 1 - 2 x + 1
ከዚህ በኋላ ገደቡ በሚከተለው ቅፅ ይከናወናል፡
ሊም x → ∞ x - 1 x + 1 x = 1 ∞ = ሊም x → ∞ 1 - 2 x + 1 x
ተለዋዋጮችን ይተኩ. እናስብ t = - x + 1 2 ⇒ 2 t = - x - 1 ⇒ x = - 2 t - 1; x → ∞ ከሆነ፣ ከዚያ t → ∞።
ከዚያ በኋላ፣ ያገኘነውን በዋናው ገደብ ውስጥ እንጽፋለን፡-
ሊም x → ∞ x - 1 x + 1 x = 1 ∞ = ሊም x → ∞ 1 - 2 x + 1 x = ሊም x → ∞ 1 + 1 ቲ - 2 ቲ - 1 = = ሊም x → ∞ 1 + 1 ቲ - 2 ቲ 1 + 1 ቲ - 1 = ሊም x → ∞ 1 + 1 ቲ - 2 ቲ ሊም x → ∞ 1 + 1 ቲ - 1 = = ሊም x → ∞ 1 + 1 ቲ - 2 1 + 1 ∞ = ሠ - 2 · (1 + 0) - 1 = ሠ - 2
ይህንን ለውጥ ለማከናወን የገደቦችን እና የስልጣኖችን መሰረታዊ ባህሪያትን ተጠቀምን።
መልስ፡-ሊም x → ∞ x - 1 x + 1 x = ሠ - 2።
ምሳሌ 3
ገደብ ሊም x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 አስላ።
መፍትሄ
ሊም x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + 1 x 3 1 + 2 x - 1 x 3 3 2 x - 5 x 4 = = 1 + 0 1 + 0 - 0 3 0 - 0 = 1 ∞
ከዚያ በኋላ, ሁለተኛውን ታላቅ ገደብ ለመተግበር ተግባሩን መለወጥ ያስፈልገናል. የሚከተለውን አግኝተናል።
ሊም x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = 1 ∞ = ሊም x → ∞ x 3 - 2 x 2 - 1 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = ሊም x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5
ሊም x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5
አሁን በክፍልፋይ አሃዛዊ እና ተከፋይ (ከስድስት ጋር እኩል) ተመሳሳይ አርቢዎች ስላሉን፣ ወሰን በሌለው የክፍልፋይ ወሰን በከፍተኛ ሀይሎች ውስጥ ካሉት የቁጥሮች ጥምርታ ጋር እኩል ይሆናል።
ሊም x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = ሊም x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 6 2 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3
t = x 2 + 2 x 2 - 1 - 2 x 2 + 2 ን በመተካት ሁለተኛ አስደናቂ ገደብ እናገኛለን። ምን ማለት ነው፡-
ሊም x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3 = lim x → ∞ 1 + 1 t t - 3 = e - 3
መልስ፡-ሊም x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = e - 3 .
መደምደሚያዎች
እርግጠኛ አለመሆን 1∞፣ i.e. ወሰን ለሌለው ኃይል አንድነት የኃይል-ሕግ እርግጠኛ አለመሆን ነው ፣ ስለሆነም ፣ የአርቢ ኃይል ተግባራትን ወሰን ለማግኘት ደንቦቹን በመጠቀም ሊገለጥ ይችላል።
በጽሁፉ ላይ ስህተት ካጋጠመህ እባክህ አድምቀው Ctrl+Enter ን ተጫን
የመጀመሪያው አስደናቂ ገደብ የሚከተለው እኩልነት ነው፡-
\ጀማሪ(እኩልታ)\lim_(\አልፋ\to(0))\frac(\sin\alpha)(\alpha)=1 \መጨረሻ(እኩል)
ለ$\alpha\to(0)$ $\sin\alpha\to(0)$ ስላለን፣ የመጀመሪያው አስደናቂ ገደብ የ$\frac(0)(0)$ ቅጽ እርግጠኛ አለመሆንን ያሳያል ይላሉ። በአጠቃላይ፣ በቀመር (1)፣ ከተለዋዋጭ $\alpha$ ይልቅ፣ ሁለት ሁኔታዎች እስካሟሉ ድረስ ማንኛውም አገላለጽ በሳይን ምልክት ስር እና በተከፋፈለው ውስጥ ሊቀመጥ ይችላል።
- በሳይን ምልክት ስር ያሉ አገላለጾች እና በዲኖሚተር ውስጥ በተመሳሳይ ጊዜ ወደ ዜሮ ይቀናበራሉ, ማለትም. የ$\frac(0)(0)$ ቅፅ እርግጠኛ አለመሆን አለ።
- በሳይን ምልክት ስር ያሉት መግለጫዎች እና በዲኖሚነሮች ውስጥ ተመሳሳይ ናቸው.
ከመጀመሪያው አስደናቂ ገደብ የተሰጡ አስተያየቶች ብዙ ጊዜ ጥቅም ላይ ይውላሉ፡
\ጀማሪ(እኩልታ) \lim_(\አልፋ\to(0))\frac(\tg\alpha)(\alpha)=1 \መጨረሻ(እኩልታ) \መጀመሪያ(ቀመር) \lim_(\አልፋ\to(0) \ frac (\arcsin \ alpha) (\ alpha) = 1 \ መጨረሻ (እኩልታ) \ መጀመሪያ (እኩልታ) \ lim_ (\ alpha \ ወደ (0)) \ frac (\arctg \ alpha) (\ alpha) = 1 \መጨረሻ(እኩል)
በዚህ ገጽ ላይ አስራ አንድ ምሳሌዎች ተፈተዋል። ምሳሌ ቁጥር 1 ለቀመር (2) - (4) ማረጋገጫ ነው. ምሳሌዎች ቁጥር 2, ቁጥር 3, ቁጥር 4 እና ቁጥር 5 ዝርዝር አስተያየቶችን የያዘ መፍትሄዎችን ይይዛሉ. ምሳሌዎች ቁጥር 6-10 ምንም አስተያየቶች የሌሉ መፍትሄዎችን ይይዛሉ, ምክንያቱም በቀደሙት ምሳሌዎች ዝርዝር ማብራሪያዎች ተሰጥተዋል. መፍትሄው ሊገኙ የሚችሉ አንዳንድ ትሪግኖሜትሪክ ቀመሮችን ይጠቀማል.
የትሪግኖሜትሪክ ተግባራት መኖራቸው እርግጠኛ ካልሆኑ $\frac (0) (0)$ ጋር ተዳምሮ የመጀመሪያውን አስደናቂ ገደብ መተግበር ማለት እንዳልሆነ ልብ ይበሉ። አንዳንድ ጊዜ ቀላል ትሪግኖሜትሪክ ለውጦች በቂ ናቸው - ለምሳሌ ይመልከቱ.
ምሳሌ ቁጥር 1
ያንን $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha) አረጋግጥ (\ alpha)=1$፣ $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$።
ሀ) ከ$\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$ ጀምሮ፣ ከዚያ፡-
$$ \lim_(\አልፋ\to(0))\frac(\tg(\አልፋ))(\አልፋ=\ግራ|\frac(0)(0)\ቀኝ| =\lim_(\አልፋ\to(0))\frac(\ኃጢአት(\አልፋ))(\አልፋ\ኮስ(\አልፋ)) $$
ከ$\lim_(\alpha\to(0))\cos(0)=1$ እና $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$ ጀምሮ ያ፡
$$ \lim_(\አልፋ\to(0))\frac(\ኃጢአት(\አልፋ))(\አልፋ\ኮስ(\አልፋ)) \ frac (\ sin (\ alpha)) (\ alpha)) (\ displaystyle \ lim_ (\ alpha \ ወደ (0)) \ cos (\ alpha)) =\frac (1) (1) =1. $$
ለ) ለውጡን $\alpha=\sin(y)$ እናድርግ። ከ$\ sin(0)=0$ ጀምሮ፣ከሁኔታው $\alpha\to(0)$ $y\to(0)$ አለን:: በተጨማሪም፣ $\arcsin\alpha=\arcsin(\sin(y))=y$ የሆነበት የዜሮ ሰፈር አለ፣ ስለዚህም፡-
$$ \lim_(\አልፋ\to(0))\frac(\arcsin\alpha)(\alpha)=\ግራ|\frac(0)(0)\ቀኝ| =\lim_(y \to(0))\frac(y)(\ sin(y)) =\lim_(y \to(0))\frac(1)(\frac(\ sin(y))) y)) =\frac(1)(\ displaystyle\lim_(y\to(0))\frac(\ sin(y))(y)) =\frac(1)(1) =1. $$
የ$\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ እኩልነት ተረጋግጧል።
ሐ) ተተኪውን $\alpha=\tg(y)$ እንሥራ። ከ$\tg(0)=0$ ጀምሮ፣ከ$\alpha\to(0)$ እና $y\to(0)$ ያሉት ሁኔታዎች እኩል ናቸው። በተጨማሪም፣ $\arctg\alpha=\arctg\tg(y))=y$ የሆነበት የዜሮ ሰፈር አለ፣ ስለዚህ፣ በነጥብ ሀ ውጤቶች ላይ በመመስረት፡ እንኖራለን፡-
$$ \lim_(\አልፋ\to(0))\frac(\arctg\alpha)(\alpha)=\ግራ|\frac(0)(0)\ቀኝ| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y \to(0))\frac(1)(\frac(\tg(y))) y)) =\frac(1)(\ displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$
የ$\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ እኩልነት ተረጋግጧል።
እኩልነት ሀ)፣ ለ)፣ ሐ) ብዙውን ጊዜ ከመጀመሪያው አስደናቂ ገደብ ጋር ጥቅም ላይ ይውላሉ።
ምሳሌ ቁጥር 2
ገደቡን አስላ $\lim_(x\to(2))\frac(\sin\ግራ(\frac(x^2-4)(x+7)\ቀኝ))(\frac(x^2-4) (x+7))$
ከ$\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ እና $\lim_( x \to(2))\ኃጢአት\ግራ(\frac(x^2-4)(x+7)\ቀኝ)=\ኃጢአት(0)=0$፣ i.e. እና ሁለቱም የክፍልፋይ አሃዛዊ እና ተከፋይ በአንድ ጊዜ ወደ ዜሮ ይቀናበራሉ፣ ከዚያ እዚህ እኛ ከ$\frac(0)(0)$ ቅጽ እርግጠኛ አለመሆን ጋር እየተገናኘን ነው፣ ማለትም። ተከናውኗል። በተጨማሪም፣ በሳይን ምልክት ስር ያሉት አገላለጾች እና በዲኖሚተር ውስጥ የተገጣጠሙ (ማለትም እና እርካታ) መሆናቸው ግልፅ ነው።
ስለዚህ, በገጹ መጀመሪያ ላይ የተዘረዘሩት ሁለቱም ሁኔታዎች ተሟልተዋል. ከዚህ በመነሳት ቀመሩ ተግባራዊ ይሆናል, ማለትም. $\lim_(x\to(2)) \frac(\ sin\ግራ(\frac(x^2-4)(x+7)\ቀኝ))(\frac(x^2-4)(x+ 7) ))=1$
መልስ: $\lim_(x\to(2))\frac(\ኃጢአት\ግራ(\frac(x^2-4)(x+7)\ቀኝ))(\frac(x^2-4)(x) +7))=1$
ምሳሌ ቁጥር 3
$\lim_(x\to(0))\frac(\sin(9x))(x)$ን ያግኙ።
ከ$\lim_(x\to(0))\sin(9x)=0$ እና $\lim_(x\to(0))x=0$ ጀምሮ፣ከ$\frac ቅጽ ላይ እርግጠኛ አለመሆንን እያስተናገድን ነው። (0)(0)$፣ i.e. ተከናውኗል። ነገር ግን በሳይን ምልክት ስር ያሉት መግለጫዎች እና በዲኖሚተር ውስጥ አይጣጣሙም. እዚህ በተፈለገው ቅፅ ላይ በዲኖሚተር ውስጥ ያለውን አገላለጽ ማስተካከል ያስፈልግዎታል. $9x$ የሚለው አገላለጽ በተከፋፈለው ውስጥ እንዲሆን እንፈልጋለን፣ ያኔ እውነት ይሆናል። በመሰረቱ፣ በተከፋፈለው ውስጥ የ$9$ እጥፍ ይጎድለናል፣ ይህም ለመግባት ያን ያህል ከባድ አይደለም—በመከፋፈያው ውስጥ ያለውን አገላለጽ በ$9$ ማባዛት። በተፈጥሮ፣ ማባዛትን በ$9$ ለማካካስ፣ ወዲያውኑ በ$9$ መከፋፈል አለቦት፡-
$$ \lim_(x\to(0))\frac(\ sin(9x))(x)=\ግራ|\frac(0)(0)\ቀኝ| =\lim_(x\to(0))\frac(\ sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\ sin) (9x))(9x)$$
አሁን በተከፋፈለው እና በሳይን ምልክት ስር ያሉት መግለጫዎች ይጣጣማሉ። ለገደቡ $\lim_(x\to(0))\frac(\ sin(9x))(9x)$ ሁለቱም ሁኔታዎች ረክተዋል። ስለዚህ፣ $\lim_(x\to(0))\frac(\ sin(9x))(9x)=1$። ይህ ማለት ደግሞ፡-
$$ 9\lim_(x\to(0))\frac(\ sin(9x))(9x)=9\cdot(1)=9። $$
መልስ: $\lim_(x\to(0))\frac(\ sin(9x))(x)=9$።
ምሳሌ ቁጥር 4
$\lim_(x\to(0))\frac(\ sin(5x))(\tg(8x))$ ያግኙ።
ከ$\lim_(x\to(0))\sin(5x)=0$ እና $\lim_(x\to(0))\tg(8x)=0$ ጀምሮ፣ እዚህ ከቅጹ እርግጠኛ አለመሆን ጋር እየተገናኘን ነው። $\frac(0)(0)$ ሆኖም ግን, የመጀመሪያው አስደናቂ ገደብ መልክ ተጥሷል. $\ sin(5x)$ የያዘ አሃዛዊ ዋጋ $5x$ ያስፈልገዋል። በዚህ ሁኔታ, ቀላሉ መንገድ አሃዛዊውን በ $ 5x$, እና ወዲያውኑ በ $ 5x$ ማባዛት ነው. በተጨማሪም $\tg(8x)$ን በ$8x$ በማባዛትና በማካፈል ከዲኖሚነተሩ ጋር ተመሳሳይ ክዋኔ እንፈጽማለን።
$$\lim_(x\to(0))\frac(\ sin(5x))(\tg(8x))=\ግራ|\frac(0)(0)\ቀኝ| =\lim_(x\to(0))\frac(\frac(\ sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
በ$x$ በመቀነስ እና ቋሚውን $\frac(5)(8)$ ከገደብ ምልክት ውጭ በመውሰድ፣ እናገኛለን፡-
$$ \lim_(x\to(0))\frac(\frac(\ sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) ) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x)) 8x)) $$
$\lim_(x\to(0))\frac(\ sin(5x))(5x)$ ለመጀመሪያው አስደናቂ ገደብ መስፈርቶቹን ሙሉ በሙሉ እንደሚያሟላ ልብ ይበሉ። $\lim_(x\to(0))\frac(\tg(8x))(8x)$ ለማግኘት የሚከተለው ቀመር ተግባራዊ ይሆናል፡-
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x) )) =\frac(5)(8)\cdot\frac(\ displaystyle\lim_(x\to(0))\frac(\ sin(5x))(5x))(\ displaystyle\lim_(x\to) (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8)። $$
መልስ: $\lim_(x\to(0))\frac(\ sin(5x))(\tg(8x))=\frac(5)(8)$።
ምሳሌ ቁጥር 5
$\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$ን ያግኙ።
ከ$\lim_(x\to(0))(\cos(5x))-\cos^3(5x)=1-1=0$ ($\cos(0)=1$) እና $\ መሆኑን አስታውስ lim_(x\to(0))x^2=0$፣ከዚያ እኛ ከ$\frac(0)(0)$ ቅጽ እርግጠኛ አለመሆን ጋር እየተገናኘን ነው። ሆኖም ግን, የመጀመሪያውን አስደናቂ ገደብ ለመተግበር ኮሳይን በቁጥር ውስጥ ማስወገድ አለብዎት, ወደ ሳይን (ፎርሙላውን ለመተግበር) ወይም ታንጀንት (ከዚያም ቀመሩን ለመተግበር). ይህ በሚከተለው ለውጥ ሊከናወን ይችላል.
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\ግራ(1-\cos^2(5x)\ቀኝ)$$$$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\ግራ(1-\cos^2(5x)\ቀኝ)=\cos(5x)\cdot\sin^2(5x)$$
ወደ ገደቡ እንመለስ፡-
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\ግራ|\frac(0)(0)\ቀኝ| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\ግራ(\cos) (5x)\cdot\frac(\sin^2(5x))(x^2)\ቀኝ) $$
ክፍልፋይ $\frac(\ sin^2(5x))(x^2)$ ለመጀመሪያው አስደናቂ ገደብ ከሚያስፈልገው ቅጽ ጋር ቅርብ ነው። ከ$\frac(\sin^2(5x))(x^2)$ ክፍልፋይ ጋር ትንሽ እንስራ፣ ከመጀመሪያው አስደናቂ ገደብ ጋር በማስተካከል (በቁጥር እና በሳይኑ ስር ያሉት አባባሎች መመሳሰል እንዳለባቸው ልብ ይበሉ)
$$\frac(\ sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\ sin^2(5x))(25x^2)=25\cdot\ግራ(\frac(\sin(5x))(5x)\ቀኝ)^2$$
ወደ ጥያቄው ገደብ እንመለስ፡-
$$ \lim_(x\to(0))\ግራ(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\ቀኝ) =\lim_(x\to(0) ))\ግራ(25\cos(5x)\cdot\ግራ(\frac(\ sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to(x) 0))\cos(5x)\cdot\lim_(x\to(0))\ግራ(\frac(\sin(5x))(5x)\ቀኝ)^2 =25\cdot(1)\cdot( 1^2) =25 $$
መልስ: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$።
ምሳሌ ቁጥር 6
ከ$\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$ ገደቡን ያግኙ።
ከ$\lim_(x\to(0))(1-\cos(6x))=0$ እና $\lim_(x\to(0))(1-\cos(2x))=0$፣ ከዚያ እርግጠኛ ካልሆንን $\frac(0)(0)$ ጋር እየተገናኘን ነው። በመጀመሪያው አስደናቂ ገደብ እርዳታ እንገልጠው. ይህንን ለማድረግ ከኮሳይንስ ወደ ሳይን እንሸጋገር። ከ$1-\cos(2\alpha)=2\sin^2(\alpha)$ ጀምሮ፣ ከዚያ፡-
$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x)$$
በተሰጠው ገደብ ውስጥ ወደ ሳይን ማለፍ፣ እኛ ይኖረናል፡-
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x)=\ግራ|\frac(0)(0)\ቀኝ| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\ sin^ 2(3x))(\ sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\ sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\ ግራ(\ frac(\ sin(3x))(3x)\ቀኝ)^2\cdot(9x^2))(\ግራ(\frac(\ sin(x))(x)\ቀኝ)^2\cdot(x^ 2)) =9\cdot\frac(\ displaystyle\lim_(x\to(0))\ግራ(\frac(\ sin(3x))(3x)\ቀኝ)^2)(\ displaystyle\lim_(x) \ወደ(0))\ግራ(\frac(\ sin(x))(x)\ቀኝ)^2) =9\cdot\frac(1^2)(1^2) =9። $$
መልስ: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$።
ምሳሌ ቁጥር 7
ገደቡን አስላ $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ በ$\alpha\neq ተገዢ \ ቤታ$
ዝርዝር ማብራሪያዎች ቀደም ብለው ተሰጥተዋል፣ ግን እዚህ እንደገና እርግጠኛ ያልሆነ $\frac(0)(0)$ እንዳለ እናስተውላለን። ቀመሩን ተጠቅመን ከኮሳይንስ ወደ ሳይን እንሸጋገር
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2)$$
ይህንን ቀመር በመጠቀም የሚከተሉትን እናገኛለን
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\ግራ|\frac(0)( 0)\ትክክል| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x)))(2)\cdot\ sin\frac(\alpha(x)) ቤታ(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\ግራኝ(x\cdot\frac(\alpha+\beta) )(2)\ቀኝ)\cdot\sin\ግራ(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to) 0)) \ ግራ (\ frac (\ sin \ ግራ (x \ cdot \ frac (\ alpha + \ beta) (2) \ ቀኝ)) (x) \ cdot \ frac (\ sin \ ግራ (x \ cdot \ frac) (\ alpha-\beta)(2)\ቀኝ))(x)\ቀኝ)=\\ =-2\cdot\lim_(x\to(0))\ግራ(\frac(\sin\ግራ)(x) \cdot\frac(\alpha+\beta)(2)\ቀኝ))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\ sin \ ግራ (x \ cdot \ frac (\ alpha-\ beta) (2) \ ቀኝ)) (x \ cdot \ frac (\ alpha-\ beta) (2)) \cdot \ frac (\ alpha- \ቤታ)(2)\ቀኝ)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ ኃጢአት ግራ(x\cdot \ frac (\ sin \ ግራ (x \ cdot \ frac (\ alpha-\ beta) (2) \ ትክክል)) (x \ cdot \ frac (\ alpha-\ beta) (2)) = - \ frac (\ alpha^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2)። $$
መልስ: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ አልፋ^2)(2)$
ምሳሌ ቁጥር 8
ገደቡን ያግኙ $\lim_(x\to(0))\frac(\tg(x)-\ sin(x))(x^3)$።
ከ$\lim_(x\to(0))(\tg(x))(\tg(x))-\sin(x))=0$ (አስታውስ $\ sin(0)=\tg(0)=0$) እና $\ lim_(x\to(0)) x^3=0$፣ እንግዲህ እዚህ ላይ ከ$\frac(0)(0)$ ቅፅ እርግጠኛ አለመሆን ጋር እየተገናኘን ነው። እንደሚከተለው እንከፋፍለው።
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\ግራ|\frac(0)(0)\ቀኝ| =\lim_(x\to(0))\frac(\frac(\ sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to() 0))\frac(\ sin(x)\cdot\ግራ(\frac(1)(\cos(x))-1\ቀኝ))(x^3) =\lim_(x\to(0)) \frac(\ sin(x)\cdot\ግራ(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\ sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot lim_(x\to(0))\ግራ(\frac(\ sin(x))(x)\cdot\ግራ 2)\ቀኝ)^2\cdot\frac(1)(\cos(x))\ቀኝ) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1) ) =\frac(1)(2)። $$
መልስ: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$።
ምሳሌ ቁጥር 9
ገደቡን ያግኙ $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$።
ከ$\lim_(x\to(3))(1-\cos(x-3))=0$ እና $\lim_(x\to(3))(x-3)\tg\frac(x -) ጀምሮ 3)(2)=0$፣ ከዚያ የ$\frac(0)(0)$ ቅጹ እርግጠኛ አለመሆን አለ። ወደ መስፋፋቱ ከመቀጠልዎ በፊት አዲሱ ተለዋዋጭ ወደ ዜሮ በሚሄድበት መንገድ ተለዋዋጭ ለውጥ ለማድረግ ምቹ ነው (በቀመሮቹ ውስጥ ተለዋዋጭ $\ alpha \u003d 0$) ። ቀላሉ መንገድ ተለዋዋጭ $t=x-3$ን ማስተዋወቅ ነው። ነገር ግን ለተጨማሪ ለውጦች ምቾት ሲባል (ይህ ጥቅም ከዚህ በታች ባለው የመፍትሄ ሂደት ውስጥ ሊታይ ይችላል) የሚከተለውን ምትክ ማድረግ ጠቃሚ ነው: $ t = \ frac (x-3) (2) $. በዚህ ጉዳይ ላይ ሁለቱም መተኪያዎች ተፈጻሚነት እንዳላቸው አስተውያለሁ, ሁለተኛው ምትክ ከክፍልፋዮች ጋር ትንሽ እንዲሰሩ የሚፈቅድልዎት ብቻ ነው. ከ$x\to(3)$፣ከ$t\to(0)$ ጀምሮ።
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\ግራ|\frac (0)(0)\ቀኝ| =\ግራ|\ጀማሪ(የተሰለፈ)&t=\frac(x-3)(2);\\&t\to(0)\መጨረሻ(የተስተካከለ)\ቀኝ| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^) 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\) ወደ(0))\frac(\ sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\ sin) (t) \cos (t)) (t) =\lim_(t\to(0))\ግራ(\frac(\ sin(t))(t)\cdot\cos(t)\ቀኝ) =\ lim_(t\to(0))\frac(\ sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1። $$
መልስ: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$።
ምሳሌ ቁጥር 10
ከ$\lim_(x\to\frac(\pi)(2))\frac(1-\ sin(x))(\ግራ(\frac(\pi)(2)-x\ቀኝ)^ ያለውን ገደብ ይፈልጉ 2)$
እንደገና እርግጠኛ ካልሆንን $\frac(0)(0)$ ጋር እየተገናኘን ነው። ወደ መስፋፋቱ ከመቀጠልዎ በፊት፣ አዲሱ ተለዋዋጭ ወደ ዜሮ በሚያዘንብ መልኩ ተለዋዋጭ ለውጥ ለማድረግ ምቹ ነው (በቀመሮቹ ውስጥ ተለዋዋጭው $\ alpha \u003d (0)$ መሆኑን ልብ ይበሉ)። ቀላሉ መንገድ ተለዋዋጭ $t=\frac(\pi)(2) -x$ ማስተዋወቅ ነው። ከ$x እስከ frac(\pi)(2)$፣ከዚያ $t\to(0)$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\ sin(x))(\ግራ(\frac(\pi)(2)-x\ቀኝ)^2) =\ግራ|\frac(0)(0)\ቀኝ| =\ግራ|\ጀማሪ(የተስተካከለ)&t=\frac(\pi)(2) -x;\\&t\to(0)\መጨረሻ(የተስተካከለ)\ቀኝ| =\lim_(t\to(0))\frac(1-\ sin\ግራ(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0) ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\ sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to) 0))\ግራ(\frac(\sin\frac(t)(2)))(\frac(t)(2))\ቀኝ)^2 = frac(1)(2)\cdot(1^2) ) =\frac(1)(2)። $$
መልስ: $\lim_(x\to\frac(\pi)(2))\frac(1-\ sin(x))(\ግራ(\frac(\pi)(2)-x\ቀኝ)^2) =\frac(1)(2)$
ምሳሌ ቁጥር 11
ወሰኖቹን ያግኙ $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$፣ $\lim_(x\to\frac(2) \ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$።
በዚህ ጉዳይ ላይ የመጀመሪያውን አስደናቂ ገደብ መጠቀም የለብንም. እባክዎ ያስታውሱ ሁለቱም የመጀመሪያው እና ሁለተኛ ገደቦች ትሪግኖሜትሪክ ተግባራትን እና ቁጥሮችን ብቻ ይይዛሉ። ብዙውን ጊዜ በእንደዚህ አይነት ምሳሌዎች በገደብ ምልክት ስር የተቀመጠውን አገላለጽ ቀላል ማድረግ ይቻላል. በተጨማሪም ፣ ከተጠቀሰው ማቅለል እና የአንዳንድ ምክንያቶች መቀነስ በኋላ እርግጠኛ አለመሆን ይጠፋል። ይህንን ምሳሌ የሰጠሁት ለአንድ ዓላማ ብቻ ነው፡ በገደብ ምልክት ስር ያሉ ትሪግኖሜትሪክ ተግባራት መኖራቸው የግድ የመጀመሪያውን አስደናቂ ገደብ መጠቀም ማለት እንዳልሆነ ለማሳየት።
ከ$\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ ጀምሮ ($\sin\frac(\pi)(2)=1$) እና $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ ( $\cos\frac(\pi)(2)=0$ን ላስታውስህ ከዛ አለን ከ$\frac(0)(0)$ ቅፅ እርግጠኛ አለመሆን ጋር መገናኘት። ይሁን እንጂ ይህ ማለት የመጀመሪያውን አስደናቂ ገደብ መጠቀም ያስፈልገናል ማለት አይደለም. እርግጠኛ አለመሆንን ለመግለጥ $\cos^2x=1-\sin^2x$ የሚለውን ግምት ውስጥ ማስገባት በቂ ነው።
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\ sin(x))(\cos^2x) =\ግራ|\frac(0)(0)\ቀኝ| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2)) \ frac (1-\ sin (x)) ((1-\ sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) \frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2)። $$
በዴሚዶቪች የመፍትሄ መጽሐፍ (ቁጥር 475) ውስጥ ተመሳሳይ መፍትሄ አለ. ስለ ሁለተኛው ገደብ፣ በዚህ ክፍል ውስጥ እንደ ቀደሙት ምሳሌዎች፣ የ$\frac(0)(0)$ ቅጽ እርግጠኛ አለመሆን አለን። ለምን ይነሳል? የሚነሳው በ$\tg\frac(2\pi)(3)=-\sqrt(3)$ እና $2\cos\frac(2\pi)(3)=-1$ ስለሆነ ነው። በቁጥር እና በቁጥር ውስጥ ያሉትን አገላለጾች ለመለወጥ እነዚህን እሴቶች እንጠቀማለን። የተግባራችን ግብ ድምርን በቁጥር እና በቁጥር እንደ ምርት መፃፍ ነው። በነገራችን ላይ ብዙውን ጊዜ በተመሳሳይ ዓይነት ውስጥ አዲሱ ተለዋዋጭ ወደ ዜሮ በሚሄድበት መንገድ የተሰራውን ተለዋዋጭ ለመለወጥ አመቺ ነው (ለምሳሌ በዚህ ገጽ ላይ ምሳሌዎች ቁጥር 9 ወይም ቁጥር 10 ይመልከቱ). ነገር ግን በዚህ ምሳሌ ውስጥ መተካት ምንም ፋይዳ የለውም, ምንም እንኳን ከተፈለገ, ተለዋዋጭ $t=x-\frac (2\pi) (3)$ን መተግበር አስቸጋሪ አይደለም.
$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\) ወደ \frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\ግራ(\cos(x)+\frac(1)(2)\ቀኝ )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\ግራ(\ cos (x)-\cos\frac(2\pi)(3)\ቀኝ))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\ sin) \ግራ(x-\frac(2\pi)(3)\ቀኝ))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac) (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3) ))\frac(\ sin\ግራ(x-\frac(2\pi)(3)\ቀኝ))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac) (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3) ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3)))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3) ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\ግራ(-\frac(1)(2)\ቀኝ)\cdot\ግራ -\frac(1)(2)\ቀኝ)) =-\frac(4)(\sqrt(3))። $$
እንደምታየው፣ የመጀመሪያውን አስደናቂ ገደብ መተግበር አልነበረብንም። በእርግጥ, ከፈለጉ ይህንን ማድረግ ይችላሉ (ከዚህ በታች ያለውን ማስታወሻ ይመልከቱ), ግን አስፈላጊ አይደለም.
የመጀመሪያውን አስደናቂ ገደብ በመጠቀም መፍትሄው ምንድን ነው? አሳይ\ደብቅ
የመጀመሪያውን አስደናቂ ገደብ በመጠቀም እናገኛለን-
$$ \lim_(x\to\frac(2\pi)(3))\frac(\ sin\ግራ(x-\frac(2\pi)(3)\ቀኝ))(-4\sin\frac) (x+ (3))=\\ =\lim_(x\to\frac(2\pi)(3))\ግራ(\frac(\sin\ግራ(x-\frac(2\pi)(3)) ቀኝ))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2))) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))) 2)\cos(x)\cos\frac(2\pi)(3))\ቀኝ) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3)) (2)\cdot\ግራ(-\frac(1)(2)\ቀኝ)\cdot\ግራ(-\frac(1)(2)\ right)) =-\frac(4)(\sqrt) 3))። $$
መልስ: $\lim_(x\to\frac(\pi)(2))\frac(1-\ sin(x))(\cos^2x)=\frac(1)(2)$፣ $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$
አስደናቂ ገደቦችን ያግኙየገደብ ንድፈ ሃሳብን ለሚማሩ ብዙ የመጀመሪያ እና ሁለተኛ አመት ተማሪዎች ብቻ ሳይሆን ለአንዳንድ አስተማሪዎችም አስቸጋሪ ነው።
ለመጀመሪያው አስደናቂ ገደብ ቀመር
የመጀመሪያው አስደናቂ ገደብ ውጤቶች
በቀመር እንፃፍ
1. 2. 3. 4. ግን አስደናቂ ገደቦች አጠቃላይ ቀመሮች በፈተና ወይም በፈተና ውስጥ ማንንም አይረዱም። ነጥቡ አሁንም ከላይ በተጻፉት ቀመሮች ላይ መድረስ እንዲችሉ እውነተኛ ስራዎች የተገነቡ ናቸው. እና አብዛኛዎቹ ተማሪዎች ክፍል ያመለጡ፣ ይህንን ኮርስ በሌሉበት ያጠኑ ወይም ራሳቸው ሁልጊዜ የሚያብራሩትን የማይረዱ አስተማሪዎች ያሏቸው፣ በጣም የመጀመሪያ ደረጃ ምሳሌዎችን በሚያስደንቅ ገደብ ማስላት አይችሉም። ከመጀመሪያው አስደናቂ ገደብ ቀመሮች ውስጥ በእነሱ እርዳታ ትሪግኖሜትሪክ ተግባራት ላሉት አገላለጾች በዜሮ የተከፋፈለው ዓይነት ዜሮ እርግጠኛ ያልሆኑ ነገሮችን ማጥናት እንደሚቻል እናያለን። አስቀድመን የመጀመሪያውን አስደናቂ ገደብ በርካታ ምሳሌዎችን እንመልከት፣ ከዚያም ሁለተኛውን አስደናቂ ገደብ እናጠና።
ምሳሌ 1. የኃጢያትን ወሰን ፈልግ (7*x)/(5*x)
መፍትሔው: እንደሚመለከቱት, ከገደቡ ስር ያለው ተግባር ከመጀመሪያው አስደናቂ ገደብ ጋር ቅርብ ነው, ነገር ግን የተግባሩ ወሰን በእርግጠኝነት ከአንድ ጋር እኩል አይደለም. በዚህ አይነት ገደብ ላይ ባሉ ተግባራት ውስጥ አንድ ሰው በሲን ስር ባለው ተለዋዋጭ ውስጥ ካለው ተመሳሳይ መጠን ያለው ተለዋዋጭ በዲኖሚነተሩ ውስጥ መምረጥ አለበት. በዚህ አጋጣሚ በ 7 ተከፋፍለው ማባዛት ![]()
ለአንዳንዶቹ እንዲህ ዓይነቱ ዝርዝር አስፈላጊ ያልሆነ ይመስላል, ነገር ግን ለአብዛኛዎቹ ተማሪዎች ገደብ ችግር ያለባቸው, ህጎቹን በተሻለ ሁኔታ እንዲረዱ እና የንድፈ ሃሳቦችን እንዲቆጣጠሩ ይረዳቸዋል.
እንዲሁም፣ የተገላቢጦሽ የተግባር አይነት ካለ፣ ይህ ደግሞ የመጀመሪያው ድንቅ ገደብ ነው። እና ሁሉም ምክንያቱም አስደናቂው ገደብ ከአንድ ጋር እኩል ነው
ተመሳሳይ ህግ በ 1 ኛ አስደናቂ ገደብ ላይ ለሚያስከትለው ውጤት ይሠራል. ስለዚህ፣ “የመጀመሪያው አስደናቂ ገደብ ምንድን ነው?” ተብሎ ከተጠየቁ። አሃድ ነው ብለህ ሳትጠራጠር መመለስ አለብህ።
ምሳሌ 2. የተግባርን ኃጢአት(6x)/ታን(11x) ወሰን አግኝ።
መፍትሄው: የመጨረሻውን ውጤት ለመረዳት, ተግባሩን በቅጹ ላይ እንጽፈው 
የአስደናቂውን ገደብ ደንቦች ለመተግበር, ማባዛት እና በምክንያቶች መከፋፈል
በመቀጠል የአንድን የተግባር ምርት ገደብ በገደብ ምርት በኩል እንጽፋለን። 
ያለ ውስብስብ ቀመሮች, የትሪግኖሜትሪክ ተግባራት ገደብ አግኝተናል. ቀላል ቀመሮችን ለመቆጣጠር፣ በ2 እና 4 ላይ ያለውን ገደብ ለማግኘት ይሞክሩ፣ የ1 አስደናቂ ወሰን ማስተባበሪያ ቀመር። ይበልጥ ውስብስብ ችግሮችን እንመለከታለን.
ምሳሌ 3፡ ገደቡን አስላ (1-cos(x))/x^2
መፍትሄ፡ በመተካት ስንፈተሽ፣ 0/0 እርግጠኛ አለመሆን እናገኛለን። ብዙ ሰዎች እንዲህ ዓይነቱን ምሳሌ ወደ አንድ አስደናቂ ገደብ እንዴት መቀነስ እንደሚችሉ አያውቁም። የትሪግኖሜትሪክ ቀመር እዚህ ጥቅም ላይ መዋል አለበት ![]()
በዚህ ሁኔታ, ገደቡ ወደ ግልጽ ቅፅ ይለወጣል 
ተግባሩን ወደ አስደናቂ ገደብ ካሬ መቀነስ ችለናል።
ምሳሌ 4፡ ገደቡን ያግኙ
መፍትሄ: በምትተካበት ጊዜ, የተለመደው ባህሪ 0/0 እናገኛለን. ሆኖም፣ ተለዋዋጭው ከዜሮ ይልቅ ወደ Pi ያዘንባል። ስለዚህ, የመጀመሪያውን አስደናቂ ገደብ ለመተግበር, አዲሱ ተለዋዋጭ ወደ ዜሮ እንዲሄድ በተለዋዋጭ x ላይ እንዲህ አይነት ለውጥ እናደርጋለን. ይህንን ለማድረግ፣ መለያውን እንደ አዲስ ተለዋዋጭ Pi-x=y እንገልፃለን። 
ስለዚህ, በቀድሞው ተግባር ውስጥ የተሰጠውን ትሪግኖሜትሪክ ቀመር በመጠቀም, ምሳሌው ወደ 1 አስደናቂ ገደብ ይቀንሳል.
ምሳሌ 5፡ ገደብ አስላ ![]() መፍትሄ: መጀመሪያ ላይ ገደቦችን እንዴት ማቃለል እንደሚቻል ግልጽ አይደለም. ግን አንድ ምሳሌ ስላለ መልሱ መኖር አለበት። ተለዋዋጭ ወደ አንድነት መሄዱ ሲተካ የዜሮ ቅጹ ባህሪ ወሰን በሌለው ተባዝቶ ስለሚሰጥ ታንጀቱ ቀመሩን በመጠቀም መተካት አለበት።
መፍትሄ: መጀመሪያ ላይ ገደቦችን እንዴት ማቃለል እንደሚቻል ግልጽ አይደለም. ግን አንድ ምሳሌ ስላለ መልሱ መኖር አለበት። ተለዋዋጭ ወደ አንድነት መሄዱ ሲተካ የዜሮ ቅጹ ባህሪ ወሰን በሌለው ተባዝቶ ስለሚሰጥ ታንጀቱ ቀመሩን በመጠቀም መተካት አለበት። ![]()
ከዚህ በኋላ አስፈላጊውን እርግጠኛ አለመሆን 0/0 እናገኛለን. በመቀጠል, በገደቡ ውስጥ የተለዋዋጮችን ለውጥ እናከናውናለን እና የንጥረትን ወቅታዊነት እንጠቀማለን 
የመጨረሻዎቹ መተኪያዎች አስደናቂውን ገደብ 1 ን እንድንጠቀም ያስችሉናል።
ሁለተኛው አስደናቂ ገደብ ከአርቢው ጋር እኩል ነው
 ይህ በእውነተኛ ገደብ ችግሮች ውስጥ ሁልጊዜ ለመድረስ ቀላል ያልሆነ ክላሲክ ነው።
ይህ በእውነተኛ ገደብ ችግሮች ውስጥ ሁልጊዜ ለመድረስ ቀላል ያልሆነ ክላሲክ ነው።
በስሌቶቹ ውስጥ ያስፈልግዎታል ገደቦች የሁለተኛው አስደናቂ ገደብ ውጤቶች ናቸው
1.  2.
2.  3.
3. ![]() 4.
4.
ለሁለተኛው አስደናቂ ገደብ እና ውጤቶቹ ምስጋና ይግባቸውና እንደ ዜሮ በዜሮ የተከፋፈለ፣ አንድም ወደ ማይታወቅ ኃይል፣ እና ወሰን የሌለው በማያልቅ የተከፋፈለ እና አልፎ ተርፎም ተመሳሳይ ደረጃ ያላቸውን ጥርጣሬዎች መመርመር ይቻላል። 
በቀላል ምሳሌዎች እንጀምር።
ምሳሌ 6. የአንድ ተግባር ወሰን ይፈልጉ
መፍትሄ፡ 2ተኛውን አስደናቂ ገደብ በቀጥታ መተግበር አይሰራም። በመጀመሪያ፣ አርቢውን በቅንፍ ውስጥ ያለውን ተገላቢጦሽ እንዲመስል መለወጥ አለብህ 
ይህ ወደ 2 ኛ አስደናቂ ገደብ የመቀነስ ቴክኒክ እና በመሠረቱ ፣ የገደቡን ተጓዳኝነት 2 ኛውን ቀመር የመቀነስ ዘዴ ነው።
ምሳሌ 7. የአንድ ተግባር ወሰን ይፈልጉ
መፍትሄ፡ ለፎርሙላ 3 የጥምረት 2 አስደናቂ ገደብ ስራዎች አሉን። ዜሮን መተካት የቅጹን ነጠላነት 0/0 ይሰጣል። ገደቡን ወደ አንድ ደንብ ከፍ ለማድረግ ፣ተለዋዋጭው በሎጋሪዝም ውስጥ ካለው ተመሳሳይ መጠን እንዲኖረው መለያውን እናዞራለን። ![]()
እንዲሁም በፈተና ውስጥ ለመረዳት እና ለማከናወን ቀላል ነው. ገደቦችን በማስላት ረገድ የተማሪዎች ችግሮች በሚከተሉት ችግሮች ይጀምራሉ።
ምሳሌ 8. የአንድ ተግባር ወሰን አስላ[(x+7)/(x-3)]^ (x-2)  መፍትሄ፡- 1 አይነት 1 ኛ አይነት ወሰን አልባ ሃይል አለን። ካላመኑኝ, በሁሉም ቦታ "X" ማለቂያ የሌለውን መተካት እና ማረጋገጥ ይችላሉ. ደንቡን ለመገንባት, የቁጥር መለኪያውን በቅንፍ ውስጥ እናካፋለን, ይህንን ለማድረግ በመጀመሪያ ማጭበርበሮችን እንሰራለን
መፍትሄ፡- 1 አይነት 1 ኛ አይነት ወሰን አልባ ሃይል አለን። ካላመኑኝ, በሁሉም ቦታ "X" ማለቂያ የሌለውን መተካት እና ማረጋገጥ ይችላሉ. ደንቡን ለመገንባት, የቁጥር መለኪያውን በቅንፍ ውስጥ እናካፋለን, ይህንን ለማድረግ በመጀመሪያ ማጭበርበሮችን እንሰራለን ![]()
አገላለጹን ወደ ገደቡ እንተካው እና ወደ 2 አስደናቂ ገደብ እንለውጠው 
ገደቡ ከ10 ገላጭ ሃይል ጋር እኩል ነው። በቅንፍም ሆነ በዲግሪ ከተለዋዋጭ ጋር የሚስማሙ ቋሚዎች ምንም “የአየር ሁኔታን” አያስተዋውቁም - ይህ መታወስ አለበት። እና አስተማሪዎችዎ "ጠቋሚውን ለምን አትቀይሩትም?" (ለዚህ ምሳሌ በ x-3 ላይ)፣ ከዚያም “ተለዋዋጭ ወደ ማለቂያ ሲይዝ፣ ከዚያ 100 ጨምሩበት ወይም 1000 ቀንስ፣ እና ገደቡ እንደነበረው ይቀራል!” ይበሉ።
የዚህ አይነት ገደቦችን ለማስላት ሁለተኛ መንገድ አለ. በሚቀጥለው ተግባር እንነጋገራለን.
ምሳሌ 9. ገደቡን ያግኙ  መፍትሄ፡ አሁን ተለዋዋጭውን በቁጥር እና በቁጥር ውስጥ አውጥተን አንዱን ባህሪ ወደ ሌላ እንቀይረው። የመጨረሻውን ዋጋ ለማግኘት፣ አስደናቂውን ገደብ የCorollary 2 ቀመር እንጠቀማለን።
መፍትሄ፡ አሁን ተለዋዋጭውን በቁጥር እና በቁጥር ውስጥ አውጥተን አንዱን ባህሪ ወደ ሌላ እንቀይረው። የመጨረሻውን ዋጋ ለማግኘት፣ አስደናቂውን ገደብ የCorollary 2 ቀመር እንጠቀማለን። 
ምሳሌ 10. የአንድ ተግባር ወሰን ይፈልጉ መፍትሄ: ሁሉም የተሰጠውን ገደብ ማግኘት አይችልም. ገደቡን ወደ 2 ከፍ ለማድረግ ኃጢአት (3x) ተለዋዋጭ እንደሆነ አስብ እና አርቢውን ማዞር ያስፈልግዎታል
መፍትሄ: ሁሉም የተሰጠውን ገደብ ማግኘት አይችልም. ገደቡን ወደ 2 ከፍ ለማድረግ ኃጢአት (3x) ተለዋዋጭ እንደሆነ አስብ እና አርቢውን ማዞር ያስፈልግዎታል 
በመቀጠል ጠቋሚውን እንደ ኃይል ወደ ኃይል እንጽፋለን 
መካከለኛ ክርክሮች በቅንፍ ውስጥ ተገልጸዋል. የመጀመሪያውን እና ሁለተኛውን አስደናቂ ገደቦች በመጠቀማችን ምክንያት ገላጭነቱን በኩብ አገኘን ።
ምሳሌ 11. የአንድ ተግባር ወሰን አስላኃጢአት(2*x)/ln(3*x+1)
መፍትሄ፡ የቅጹ 0/0 እርግጠኛ አለመሆን አለን። በተጨማሪም, ተግባሩ ሁለቱንም አስደናቂ ገደቦች ለመጠቀም መለወጥ እንዳለበት እናያለን. የቀደመውን የሂሳብ ለውጦችን እናከናውን። ![]()
በተጨማሪም, ያለምንም ችግር, ገደቡ ዋጋውን ይወስዳል 
ተግባራትን በፍጥነት መፃፍ እና ወደ መጀመሪያው ወይም ሁለተኛው አስደናቂ ገደብ እንዲቀንሱ ከተማሩ በምድብ ፣ በፈተናዎች ፣ በሞጁሎች ላይ እንደዚህ ያለ ነፃነት ይሰማዎታል ። ገደቦችን ለማግኘት የተሰጡትን ዘዴዎች ለማስታወስ ለእርስዎ አስቸጋሪ ከሆነ ሁልጊዜ ከእኛ ገደቦች ላይ የሙከራ ወረቀት ማዘዝ ይችላሉ።
ይህንን ለማድረግ ቅጹን ይሙሉ, ውሂብ ያቅርቡ እና አንድ ፋይል በምሳሌዎች ያያይዙ. ብዙ ተማሪዎችን ረድተናል - እርስዎንም ልንረዳዎ እንችላለን!
ብዙ አስደናቂ ገደቦች አሉ ፣ ግን በጣም ዝነኞቹ የመጀመሪያዎቹ እና ሁለተኛው አስደናቂ ገደቦች ናቸው። የእነዚህ ገደቦች አስደናቂው ነገር በሰፊው ጥቅም ላይ የዋሉ እና በእነሱ እርዳታ በብዙ ችግሮች ውስጥ የሚገኙ ሌሎች ገደቦችን ማግኘት ይችላሉ ። በዚህ ትምህርት ተግባራዊ ክፍል ውስጥ የምናደርገው ይህንን ነው። ችግሮችን ወደ መጀመሪያው ወይም ሁለተኛው አስደናቂ ገደብ በመቀነስ ለመፍታት ፣ የእነዚህ ገደቦች እሴቶች በታላላቅ የሂሳብ ሊቃውንት የተወሰዱ ስለሆኑ በእነሱ ውስጥ ያሉትን እርግጠኛ ያልሆኑትን መግለጥ አያስፈልግም።
የመጀመሪያው አስደናቂ ገደብበራዲያን መስፈሪያ የተገለጸው የአንድ የማይገደብ ቅስት ሳይን ጥምርታ ወሰን ተብሎ ይጠራል፡
ወደ መጀመሪያው አስደናቂ ገደብ ችግሮችን ወደ መፍታት እንሂድ። ማስታወሻ፡ በገደብ ምልክት ስር የትሪግኖሜትሪክ ተግባር ካለ፣ ይህ አገላለጽ ወደ መጀመሪያው አስደናቂ ገደብ እንደሚቀንስ እርግጠኛ የሆነ ምልክት ነው።
ምሳሌ 1.ገደቡን ያግኙ።
መፍትሄ። በምትኩ መተካት xዜሮ ወደ አለመተማመን ይመራል
![]() .
.
መለያው ሳይን ነው፣ ስለዚህ አገላለጹ ወደ መጀመሪያው አስደናቂ ገደብ ሊመጣ ይችላል። ለውጡን እንጀምር፡-
![]() .
.
መለያው የሶስት ኤክስ ሳይን ነው ፣ ግን አሃዛዊው አንድ X ብቻ ነው ያለው ፣ ይህ ማለት በቁጥር ውስጥ ሶስት X ማግኘት ያስፈልግዎታል ማለት ነው ። ለምንድነው፧ ለማስተዋወቅ 3 x = ሀእና መግለጫውን ያግኙ።
እና ወደ የመጀመሪያው አስደናቂ ገደብ ልዩነት ደርሰናል፡-
ምክንያቱም በዚህ ቀመር ውስጥ የትኛው ፊደል (ተለዋዋጭ) ከኤክስ ይልቅ ቢቆም ምንም ለውጥ አያመጣም።
Xን በሦስት እናባዛለን እና ወዲያውኑ እንካፈላለን-
 .
.
በታየው የመጀመሪያው አስደናቂ ገደብ መሰረት፣ ክፍልፋይ አገላለጽ እንተካለን፡-
አሁን ይህንን ገደብ በመጨረሻ መፍታት እንችላለን-
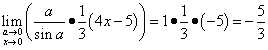 .
.
ምሳሌ 2.ገደቡን ያግኙ።
መፍትሄ። ቀጥተኛ መተካት እንደገና ወደ “ዜሮ በዜሮ የተከፈለ” እርግጠኛ አለመሆንን ያስከትላል።
![]() .
.
የመጀመሪያውን አስደናቂ ገደብ ለማግኘት በቁጥር ውስጥ ባለው የሲን ምልክት ስር ያለው x እና በመጠኑ ውስጥ ያለው x ተመሳሳይ መጠን እንዲኖራቸው ያስፈልጋል። ይህ ጥምርታ ከ 2 ጋር እኩል ይሁን። ይህንን ለማድረግ አሁን ያለውን የ x መጠን ከዚህ በታች ባለው መልኩ አስቡት፣ ክዋኔዎችን ከክፍልፋዮች ጋር በማከናወን፣ እናገኛለን፡-
 .
.
ምሳሌ 3.ገደቡን ያግኙ።
መፍትሄ። በምንተካበት ጊዜ፣ እርግጠኛ አለመሆን “ዜሮ በዜሮ የተከፈለ” እንደገና እናገኛለን፡-
 .
.
ምናልባት ከመጀመሪያው አገላለጽ የመጀመሪያውን አስደናቂ ገደብ በመጀመሪያው አስደናቂ ገደብ ማባዛት እንደሚችሉ አስቀድመው ተረድተው ይሆናል. ይህንን ለማድረግ የ x ካሬዎችን በቁጥር እና በሲን ውስጥ በዲኖሚነተር ውስጥ ወደ ተመሳሳይ ምክንያቶች እናጠፋለን, እና ለ x እና sine ተመሳሳይ መለኪያዎችን ለማግኘት የ x ን በቁጥር በ 3 እንከፍላለን እና ወዲያውኑ እናባዛለን። በ 3. እናገኛለን:
 .
.
ምሳሌ 4.ገደቡን ያግኙ።
መፍትሄ። አሁንም “ዜሮ በዜሮ የተከፈለ” እርግጠኛ አለመሆንን እናገኛለን፡-
![]() .
.
የመጀመሪያዎቹን ሁለት አስደናቂ ገደቦች ጥምርታ ማግኘት እንችላለን። ሁለቱንም አሃዛዊ እና ተከፋይ በ x እንካፈላለን. ከዚያም የሳይንስ እና የ xes መለኪያዎች እንዲገጣጠሙ የላይኛውን x በ 2 እናባዛለን እና ወዲያውኑ በ 2 እንካፈላለን እና የታችኛውን x በ 3 እናባዛለን እና ወዲያውኑ በ 3 እንካፈላለን ።

ምሳሌ 5.ገደቡን ያግኙ።
መፍትሄ። እና እንደገና “ዜሮ በዜሮ የተከፈለ” እርግጠኛ አለመሆን፡-
ከትሪግኖሜትሪ እናስታውሳለን ታንጀንት የሳይን እና ኮሳይን ጥምርታ ነው፣ እና የዜሮ ኮሳይን ከአንድ ጋር እኩል ነው። ለውጦችን እናከናውናለን እና እናገኛለን:
 .
.
ምሳሌ 6.ገደቡን ያግኙ።
መፍትሄ። በገደብ ምልክት ስር ያለው ትሪግኖሜትሪክ ተግባር እንደገና የመጀመሪያውን አስደናቂ ገደብ መጠቀምን ይጠቁማል። እንደ ሳይን እና ኮሳይን ጥምርታ እንወክለዋለን።
ይህ መጣጥፍ፡- “ሁለተኛው አስደናቂ ገደብ” በቅጹ ላይ እርግጠኛ ባልሆኑት ገደቦች ውስጥ ለመግለፅ የተወሰነ ነው።
$ \bigg [\frac (\ infty) (\ infty) \bigg]^\ infty $ እና $ ^\infty $.
እንዲሁም እንደነዚህ ያሉ እርግጠኛ ያልሆኑ ሁኔታዎች የአርቢ ተግባሩን ሎጋሪዝም በመጠቀም ሊገለጡ ይችላሉ, ነገር ግን ይህ ሌላ የመፍትሄ ዘዴ ነው, ይህም በሌላ ጽሑፍ ውስጥ ይሸፈናል.
ቀመር እና ውጤቶች
ፎርሙላሁለተኛው አስደናቂ ገደብ እንደሚከተለው ተጽፏል፡- $$ \lim_(x \to \ infty) \bigg (1+\frac(1)(x)\bigg)^x = e፣ \text( where ) e \approx 2.718 $$
ከቀመርው ይከተላል ውጤቶችምሳሌዎችን ከገደብ ጋር ለመፍታት ለመጠቀም በጣም ምቹ ናቸው፡$$ \lim_(x \to \ infty) \bigg (1 + \frac(k)(x) \bigg)^x = e^k፣ \text( የት ) k \በ \mathbb(R) $$$$ \lim_(x \to \ infty) \bigg (1 + \frac(1)(f(x)) \bigg)^(f(x)) = ሠ $$$ \lim_(x \ ወደ 0) \bigg (1 + x \bigg)^\frac(1)(x) = ሠ $$
ሁለተኛው አስደናቂ ገደብ ሁልጊዜ ገላጭ ተግባር ላይ ሊተገበር እንደማይችል ልብ ሊባል የሚገባው ነው, ነገር ግን መሰረቱ ወደ አንድነት በሚሄድበት ጊዜ ብቻ ነው. ይህንን ለማድረግ በመጀመሪያ በአዕምሯዊ ሁኔታ የመሠረቱን ገደብ ያሰሉ, ከዚያም መደምደሚያዎችን ይሳሉ. ይህ ሁሉ በምሳሌ መፍትሄዎች ውስጥ ይብራራል.
የመፍትሄዎች ምሳሌዎች
ቀጥተኛውን ቀመር እና ውጤቶቹን በመጠቀም የመፍትሄ ምሳሌዎችን እንመልከት። ቀመሩ የማይፈለግባቸውን ጉዳዮችም እንመረምራለን። ዝግጁ የሆነውን መልስ ብቻ መጻፍ በቂ ነው.
| ምሳሌ 1 |
| ከ$ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) $ ያለውን ገደብ ያግኙ |
| መፍትሄ |
|
ገደብ የለሽነትን ወደ ገደቡ እንተካው እና እርግጠኛ አለመሆንን እንመልከት፡$$ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) = \bigg (\ frac (\ infty) (\ infty) \bigg) ^ \ ኢንፍቲ $$ የመሠረቱን ወሰን እንፈልግ፡$$ \lim_(x\to\infty) \frac(x+4)(x+3)= \lim_(x\to\infty) \frac(x(1+\frac) (4)() x)))(x(1+\frac(3)(x)))) = 1$$ ከአንድ ጋር እኩል የሆነ መሠረት አግኝተናል, ይህም ማለት ሁለተኛውን አስደናቂ ገደብ አስቀድመን መተግበር እንችላለን. ይህንን ለማድረግ አንዱን በመቀነስ እና በመጨመር የተግባሩን መሰረት ወደ ቀመር እናስተካክለው፡- $$ \lim_(x\to\infty) \bigg(1 + \frac(x+4)(x+3) - 1 \bigg)^(x+3) = \lim_(x\to\infty) \ big(1 + \frac(1)(x+3) \bigg)^(x+3) =$$ ሁለተኛውን ገለጻ እንይና መልሱን ጻፍ፡- $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = ሠ $$ ችግርዎን መፍታት ካልቻሉ ወደ እኛ ይላኩልን። ዝርዝር መፍትሄ እናቀርባለን። የስሌቱን ሂደት ለማየት እና መረጃ ለማግኘት ይችላሉ. ይህ በጊዜው ከአስተማሪዎ ክፍልዎን እንዲያገኙ ይረዳዎታል! |
| መልስ |
| $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = ሠ $$ |
| ምሳሌ 4 |
| ገደቡን ይፍቱ $ \lim_(x \ ወደ \ infty) \bigg (\frac (3x^2+4) (3x^2-2) \bigg) ^ (3x) $ |
| መፍትሄ |
|
የመሠረቱን ወሰን እናገኛለን እና $ \lim_(x \ to\ infty) \ frac (3x^2+4) (3x^2-2) = 1 $ን እናያለን ይህም ማለት ሁለተኛውን አስደናቂ ገደብ መተግበር እንችላለን ማለት ነው። በመደበኛ ዕቅዱ መሠረት ከዲግሪው መሠረት አንዱን እንጨምራለን እና እንቀንሳለን- $$ \lim_(x\to \ infty) \bigg (1+\frac(3x^2+4)(3x^2-2)-1 \bigg) ^(3x) = \lim_(x\to \infty) ) \bigg (1+\frac(6)(3x^2-2) \bigg) ^(3x) = $$ ክፍልፋዩን ወደ 2 ኛ ማስታወሻ ቀመር እናስተካክላለን. ገደብ፡ $$ = \lim_(x\to \ infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(3x) =$$ አሁን ዲግሪውን እናስተካክል. ኃይሉ ከመሠረቱ $ \frac(3x^2-2)(6) $ ጋር እኩል የሆነ ክፍልፋይ መያዝ አለበት። ይህንን ለማድረግ, ማባዛት እና ዲግሪውን በእሱ ይከፋፍሉት እና መፍታትዎን ይቀጥሉ: $$ = \lim_(x\to \ infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(\frac(3x^2-2) (6) \cdot \frac(6)(3x^2-2)\cdot 3x) = \lim_(x\to \infty) e^(\frac(18x)(3x^2-2)) = $$ በ$ e $ ላይ ያለው ሃይል ያለው ገደብ፡ $ \lim_(x\to \infty) \frac(18x)(3x^2-2) = 0$ ጋር እኩል ነው። ስለዚህ መፍትሄውን እንቀጥላለን- |
| መልስ |
| $$ \lim_(x\to \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) = 1 $$ |
ችግሩ ከሁለተኛው አስደናቂ ገደብ ጋር ተመሳሳይነት ያለው, ነገር ግን ያለሱ ሊፈታ የሚችልባቸውን ጉዳዮች እንመልከት.
በአንቀጹ ውስጥ: "ሁለተኛው አስደናቂ ገደብ: የመፍትሄዎች ምሳሌዎች" ቀመሩ, ውጤቶቹ ተተነተኑ እና በዚህ ርዕስ ላይ የተለመዱ የችግሮች ዓይነቶች ተሰጥተዋል.
