Et simultant system av lineære ligninger har en unik løsning. Metoder for å løse systemer av lineære ligninger
Eksempel 1. Finn en generell løsning og en spesiell løsning av systemetLøsning Vi gjør det ved hjelp av en kalkulator. La oss skrive ut den utvidede og hovedmatrisen: 
Hovedmatrisen A er atskilt med en stiplet linje. Vi skriver ukjente systemer øverst, med tanke på mulig omorganisering av ledd i systemets likninger. Ved å bestemme rangeringen til den utvidede matrisen, finner vi samtidig rangeringen til hovedmatrisen. I matrise B er første og andre kolonne proporsjonale. Av de to proporsjonale kolonnene kan bare én falle inn i den grunnleggende moll, så la oss for eksempel flytte den første kolonnen forbi den stiplede linjen med motsatt fortegn. For systemet betyr dette å overføre ledd fra x 1 til høyre side av ligningene. 
La oss redusere matrisen til trekantet form. Vi vil bare jobbe med rader, siden å multiplisere en matriserad med et annet tall enn null og legge den til en annen rad for systemet betyr å multiplisere ligningen med det samme tallet og legge den til med en annen ligning, som ikke endrer løsningen av system. Vi jobber med den første raden: multipliser den første raden i matrisen med (-3) og legg til den andre og tredje raden etter tur. Multipliser deretter den første linjen med (-2) og legg den til den fjerde. 
Den andre og tredje linjen er proporsjonale, derfor kan en av dem, for eksempel den andre, krysses ut. Dette tilsvarer å krysse ut den andre ligningen i systemet, siden den er en konsekvens av den tredje. 
Nå jobber vi med den andre linjen: multipliser den med (-1) og legg den til den tredje. 
Den stiplede moll har den høyeste orden (av de mulige moll) og er ikke-null (den er lik produktet av elementene på hoveddiagonalen), og denne moll tilhører både hovedmatrisen og den utvidede, derfor rangA = rangB = 3.
Liten  er grunnleggende. Den inkluderer koeffisienter for de ukjente x 2 , x 3 , x 4 , som betyr at de ukjente x 2 , x 3 , x 4 er avhengige, og x 1 , x 5 er frie.
er grunnleggende. Den inkluderer koeffisienter for de ukjente x 2 , x 3 , x 4 , som betyr at de ukjente x 2 , x 3 , x 4 er avhengige, og x 1 , x 5 er frie.
La oss transformere matrisen, og la bare basis-moll til venstre (som tilsvarer punkt 4 i løsningsalgoritmen ovenfor). 
Systemet med koeffisientene til denne matrisen er ekvivalent med det opprinnelige systemet og har formen

Ved å bruke metoden for å eliminere ukjente finner vi: ![]() , ,
, ,
Vi oppnådde relasjoner som uttrykker de avhengige variablene x 2, x 3, x 4 gjennom de frie x 1 og x 5, det vil si at vi fant en generell løsning: 
Ved å tilordne noen verdier til de gratis ukjente, får vi et hvilket som helst antall spesielle løsninger. La oss finne to spesielle løsninger:
1) la x 1 = x 5 = 0, deretter x 2 = 1, x 3 = -3, x 4 = 3;
2) sett x 1 = 1, x 5 = -1, deretter x 2 = 4, x 3 = -7, x 4 = 7.
Dermed ble det funnet to løsninger: (0,1,-3,3,0) – en løsning, (1,4,-7,7,-1) – en annen løsning.
Eksempel 2. Utforsk kompatibilitet, finn en generell og én spesiell løsning på systemet 
Løsning. La oss omorganisere den første og andre ligningen slik at den har en i den første ligningen og skrive matrisen B. 
Vi får nuller i den fjerde kolonnen ved å operere med den første raden: 
Nå får vi nullene i den tredje kolonnen ved å bruke den andre linjen: 
 Den tredje og fjerde linjen er proporsjonale, så en av dem kan krysses ut uten å endre rangeringen:
Den tredje og fjerde linjen er proporsjonale, så en av dem kan krysses ut uten å endre rangeringen:
Multipliser den tredje linjen med (–2) og legg den til den fjerde: 
Vi ser at rekkene til hoved- og utvidede matriser er lik 4, og rangeringen faller sammen med antall ukjente, derfor har systemet en unik løsning:
;
x 4 = 10- 3x 1 – 3x 2 – 2x 3 = 11.
Eksempel 3. Undersøk systemet for kompatibilitet og finn en løsning hvis den eksisterer. 
Løsning. Vi komponerer en utvidet matrise av systemet. 
 Vi omorganiserer de to første ligningene slik at det er 1 i øvre venstre hjørne:
Vi omorganiserer de to første ligningene slik at det er 1 i øvre venstre hjørne:
Multipliser den første linjen med (-1), legg den til den tredje: 
Multipliser den andre linjen med (-2) og legg den til den tredje: 
Systemet er inkonsekvent, siden vi i hovedmatrisen fikk en rad bestående av nuller, som krysses ut når rangeringen er funnet, men i den utvidede matrisen forblir den siste raden, det vil si r B > r A .
Trening. Undersøk dette likningssystemet for kompatibilitet og løs det ved hjelp av matriseregning.
Løsning
Eksempel. Bevis kompatibiliteten til systemet med lineære ligninger og løs det på to måter: 1) ved Gauss-metoden; 2) Cramers metode. (skriv inn svaret på skjemaet: x1,x2,x3)
Løsning :doc :doc :xls
Svar: 2,-1,3.
Eksempel. Et system med lineære ligninger er gitt. Bevis dens kompatibilitet. Finn en generell løsning av systemet og en spesiell løsning.
Løsning
Svar: x 3 = - 1 + x 4 + x 5; x 2 = 1 - x 4; x 1 = 2 + x 4 - 3 x 5
Trening. Finn de generelle og spesielle løsningene for hvert system.
Løsning. Vi studerer dette systemet ved å bruke Kronecker-Capelli-teoremet.
La oss skrive ut den utvidede og hovedmatrisen:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Her er matrise A uthevet med fet skrift.
La oss redusere matrisen til trekantet form. Vi vil bare jobbe med rader, siden å multiplisere en matriserad med et annet tall enn null og legge den til en annen rad for systemet betyr å multiplisere ligningen med det samme tallet og legge den til med en annen ligning, som ikke endrer løsningen av system.
La oss gange den første linjen med (3). Multipliser den andre linjen med (-1). La oss legge til den andre linjen til den første:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
La oss gange den andre linjen med (2). Multipliser den tredje linjen med (-3). La oss legge til den tredje linjen til den andre:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Multipliser den andre linjen med (-1). La oss legge til den andre linjen til den første:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Den valgte moll har den høyeste orden (av mulige moll) og er ikke-null (den er lik produktet av elementene på motsatt diagonal), og denne moll tilhører både hovedmatrisen og den utvidede, derfor rang( A) = rang(B) = 3 Siden rangeringen til hovedmatrisen er lik rangeringen til den utvidede matrisen, systemet er samarbeidende.
Denne mindre er grunnleggende. Den inkluderer koeffisienter for de ukjente x 1 , x 2 , x 3 , som betyr at de ukjente x 1 , x 2 , x 3 er avhengige (grunnleggende), og x 4 , x 5 er frie.
La oss transformere matrisen, slik at bare basis-moll er igjen til venstre.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
27x 3 =
- x 2 + 13x 3 = - 1 + 3x 4 - 6x 5
2x 1 + 3x 2 - 3x 3 = 1 - 3x 4 + 2x 5
Ved å bruke metoden for å eliminere ukjente finner vi:
Vi oppnådde relasjoner som uttrykker de avhengige variablene x 1 , x 2 , x 3 gjennom de frie x 4 , x 5 , det vil si at vi fant felles vedtak:
x 3 = 0
x 2 = 1 - 3x 4 + 6x 5
x 1 = - 1 + 3x 4 - 8x 5
usikker, fordi har mer enn én løsning.
Trening. Løs ligningssystemet.
Svar:x 2 = 2 - 1,67x 3 + 0,67x 4
x 1 = 5 - 3,67 x 3 + 0,67 x 4
Ved å tilordne noen verdier til de gratis ukjente, får vi et hvilket som helst antall spesielle løsninger. Systemet er usikker
Som det fremgår av Cramers teorem, når du løser et system med lineære ligninger, kan tre tilfeller oppstå:
Første tilfelle: et system med lineære ligninger har en unik løsning
(systemet er konsistent og bestemt)
 Andre tilfelle: et system med lineære ligninger har et uendelig antall løsninger
Andre tilfelle: et system med lineære ligninger har et uendelig antall løsninger
(systemet er konsekvent og usikkert)
** ![]() ,
,
de. koeffisientene til de ukjente og de frie leddene er proporsjonale.
 Tredje tilfelle: systemet med lineære ligninger har ingen løsninger
Tredje tilfelle: systemet med lineære ligninger har ingen løsninger
(systemet er inkonsekvent)
Så systemet m lineære ligninger med n kalt variabler ikke-ledd, hvis hun ikke har en eneste løsning, og ledd, hvis den har minst én løsning. Et simultant ligningssystem som bare har én løsning kalles sikker, og mer enn én – usikker.
Eksempler på løsning av systemer av lineære ligninger ved bruk av Cramer-metoden
La systemet være gitt
 .
.
Basert på Cramers teorem
………….
,
Hvor  -
-
systemdeterminant. Vi får de gjenværende determinantene ved å erstatte kolonnen med koeffisientene til den tilsvarende variabelen (ukjent) med frie termer:



Eksempel 2.
 .
.

Derfor er systemet klart. For å finne løsningen beregner vi determinantene



Ved å bruke Cramers formler finner vi:
![]()
Så, (1; 0; -1) er den eneste løsningen på systemet.
For å sjekke løsningene til likningssystemene 3 X 3 og 4 X 4, kan du bruke en online kalkulator som bruker Cramers løsningsmetode.
Hvis det i et system av lineære ligninger ikke er noen variabler i en eller flere ligninger, så er de tilsvarende elementene i determinanten lik null! Dette er neste eksempel.
Eksempel 3. Løs et system med lineære ligninger ved å bruke Cramer-metoden:
 .
.
Løsning. Vi finner determinanten for systemet:

Se nøye på likningssystemet og på systemets determinant og gjenta svaret på spørsmålet i hvilke tilfeller ett eller flere elementer i determinanten er lik null. Så determinanten er ikke lik null, derfor er systemet bestemt. For å finne løsningen beregner vi determinantene for de ukjente



Ved å bruke Cramers formler finner vi:
Så løsningen på systemet er (2; -1; 1).
6. Generelt system av lineære algebraiske ligninger. Gauss metode.
Som vi husker er Cramers regel og matrisemetoden uegnet i tilfeller der systemet har uendelig mange løsninger eller er inkonsekvent. Gauss metode – det kraftigste og mest allsidige verktøyet for å finne løsninger på ethvert system av lineære ligninger, hvilken i hvert tilfelle vil lede oss til svaret! Selve metodealgoritmen fungerer likt i alle tre tilfellene. Hvis Cramer- og matrisemetodene krever kunnskap om determinanter, trenger du kun kunnskap om aritmetiske operasjoner for å anvende Gauss-metoden, noe som gjør den tilgjengelig selv for grunnskoleelever.
Først, la oss systematisere litt kunnskap om systemer med lineære ligninger. Et system med lineære ligninger kan:
1) Ha en unik løsning.
2) Har uendelig mange løsninger.
3) Har ingen løsninger (vær ikke-ledd).
Gauss-metoden er det kraftigste og mest universelle verktøyet for å finne en løsning noen systemer av lineære ligninger. Som vi husker, Cramers regel og matrisemetode er uegnet i tilfeller hvor systemet har uendelig mange løsninger eller er inkonsekvent. Og metoden for sekvensiell eliminering av ukjente Uansett vil lede oss til svaret! I denne leksjonen vil vi igjen vurdere Gauss-metoden for sak nr. 1 (den eneste løsningen på systemet), artikkelen er viet situasjonene i punkt nr. 2-3. Jeg legger merke til at algoritmen til selve metoden fungerer likt i alle tre tilfellene.
La oss gå tilbake til det enkleste systemet fra leksjonen Hvordan løse et system med lineære ligninger?
og løse det ved hjelp av Gauss-metoden.
Det første trinnet er å skrive ned utvidet systemmatrise:
. Jeg tror alle kan se etter hvilket prinsipp koeffisientene er skrevet. Den vertikale linjen inne i matrisen har ingen matematisk betydning - den er rett og slett en gjennomstreking for enkel design.
Henvisning:Jeg anbefaler deg å huske vilkår lineær algebra. Systemmatrise er en matrise som kun består av koeffisienter for ukjente, i dette eksemplet matrisen til systemet: . Utvidet systemmatrise– dette er den samme matrisen til systemet pluss en kolonne med frie termer, i dette tilfellet: . For korthets skyld kan enhver av matrisene ganske enkelt kalles en matrise.
Etter at den utvidede systemmatrisen er skrevet, er det nødvendig å utføre noen handlinger med den, som også kalles elementære transformasjoner.
Følgende elementære transformasjoner eksisterer:
1) Strenger matriser kan omorganiseres noen steder. For eksempel, i matrisen under vurdering, kan du smertefritt omorganisere den første og andre raden: 
2) Hvis det er (eller har dukket opp) proporsjonale (som et spesialtilfelle - identiske) rader i matrisen, bør du slette fra matrisen alle disse radene unntatt én. Tenk for eksempel på matrisen  . I denne matrisen er de tre siste radene proporsjonale, så det er nok å forlate bare en av dem:
. I denne matrisen er de tre siste radene proporsjonale, så det er nok å forlate bare en av dem:  .
.
3) Hvis det vises en nullrad i matrisen under transformasjoner, bør den også være det slette. Jeg vil ikke tegne, selvfølgelig, nulllinjen er linjen der alle nuller.
4) Matriseraden kan være multiplisere (dividere) til et hvilket som helst nummer ikke-null. Tenk for eksempel på matrisen . Her er det lurt å dele den første linjen med –3, og multiplisere den andre linjen med 2:  . Denne handlingen er veldig nyttig fordi den forenkler ytterligere transformasjoner av matrisen.
. Denne handlingen er veldig nyttig fordi den forenkler ytterligere transformasjoner av matrisen.
5) Denne transformasjonen forårsaker de fleste vanskelighetene, men faktisk er det heller ikke noe komplisert. Til en rad av en matrise kan du legg til en annen streng multiplisert med et tall, forskjellig fra null. La oss se på matrisen vår fra et praktisk eksempel: . Først skal jeg beskrive transformasjonen i detalj. Multipliser den første linjen med –2:  , Og til den andre linjen legger vi den første linjen multiplisert med –2:
, Og til den andre linjen legger vi den første linjen multiplisert med –2:  . Nå kan den første linjen deles "tilbake" med –2: . Som du kan se, er linjen som legges til LI – har ikke endret seg. Alltid linjen SOM LEGGES TIL endres UT.
. Nå kan den første linjen deles "tilbake" med –2: . Som du kan se, er linjen som legges til LI – har ikke endret seg. Alltid linjen SOM LEGGES TIL endres UT.
I praksis skriver de det selvfølgelig ikke så detaljert, men skriver det kort: 
Nok en gang: til andre linje lagt til den første linjen multiplisert med –2. En linje multipliseres vanligvis muntlig eller på et utkast, med mentalberegningsprosessen omtrent slik:
"Jeg skriver om matrisen og skriver om den første linjen:  »
»
"Første kolonne. Nederst må jeg få null. Derfor multipliserer jeg den øverst med –2: , og legger den første til den andre linjen: 2 + (–2) = 0. Jeg skriver resultatet i den andre linjen:  »
»
«Nå den andre kolonnen. Øverst ganger jeg -1 med -2: . Jeg legger den første til den andre linjen: 1 + 2 = 3. Jeg skriver resultatet i den andre linjen:  »
»
«Og den tredje kolonnen. Øverst multipliserer jeg -5 med -2: . Jeg legger den første til den andre linjen: –7 + 10 = 3. Jeg skriver resultatet i den andre linjen:  »
»
Vennligst forstå dette eksemplet nøye og forstå sekvensberegningsalgoritmen, hvis du forstår dette, er Gauss-metoden praktisk talt i lommen. Men vi skal selvfølgelig fortsatt jobbe med denne transformasjonen.
Elementære transformasjoner endrer ikke løsningen av ligningssystemet
! MERK FØLGENDE: betraktet som manipulasjoner kan ikke bruke, hvis du blir tilbudt en oppgave der matrisene er gitt «av seg selv». For eksempel med "klassisk" operasjoner med matriser Under ingen omstendigheter bør du omorganisere noe inne i matrisene!
La oss gå tilbake til systemet vårt. Det er praktisk talt tatt i stykker.
La oss skrive ned den utvidede matrisen til systemet og ved å bruke elementære transformasjoner redusere den til trinnvis utsikt:

(1) Den første linjen ble lagt til den andre linjen, multiplisert med –2. Og igjen: hvorfor multipliserer vi den første linjen med –2? For å få null nederst, som betyr å bli kvitt en variabel i den andre linjen.
(2) Del den andre linjen med 3.
Hensikten med elementære transformasjoner –
reduser matrisen til trinnvis form:  . I utformingen av oppgaven markerer de bare "trappen" med en enkel blyant, og ringer også rundt tallene som er plassert på "trinnene". Begrepet «trinnsyn» i seg selv er ikke helt teoretisk; i vitenskapelig og pedagogisk litteratur kalles det ofte trapesformet utsikt eller trekantet utsikt.
. I utformingen av oppgaven markerer de bare "trappen" med en enkel blyant, og ringer også rundt tallene som er plassert på "trinnene". Begrepet «trinnsyn» i seg selv er ikke helt teoretisk; i vitenskapelig og pedagogisk litteratur kalles det ofte trapesformet utsikt eller trekantet utsikt.
Som et resultat av elementære transformasjoner fikk vi tilsvarende opprinnelige ligningssystem:
Nå må systemet "avvikles" i motsatt retning - fra bunn til topp kalles denne prosessen invers av Gauss-metoden.
I den nedre ligningen har vi allerede et ferdig resultat: .
La oss vurdere den første ligningen til systemet og erstatte den allerede kjente verdien av "y" i den:
La oss vurdere den vanligste situasjonen når Gauss-metoden krever å løse et system med tre lineære ligninger med tre ukjente.
Eksempel 1
Løs ligningssystemet ved å bruke Gauss-metoden: 
La oss skrive den utvidede matrisen til systemet: 
Nå vil jeg umiddelbart tegne resultatet som vi kommer til under løsningen: 
Og jeg gjentar, målet vårt er å bringe matrisen til en trinnvis form ved hjelp av elementære transformasjoner. Hvor skal jeg starte?
Se først på nummeret øverst til venstre: 
Burde nesten alltid være her enhet. Generelt sett vil –1 (og noen ganger andre tall) gjøre det, men på en eller annen måte har det tradisjonelt skjedd at man vanligvis plasseres der. Hvordan organisere en enhet? Vi ser på den første kolonnen - vi har en ferdig enhet! Transformasjon én: bytt første og tredje linje: 
Nå vil den første linjen forbli uendret til slutten av løsningen. Nå fint.
Enheten i øverste venstre hjørne er organisert. Nå må du få nuller på disse stedene: 
Vi får nuller ved å bruke en "vanskelig" transformasjon. Først tar vi for oss den andre linjen (2, –1, 3, 13). Hva må gjøres for å få null i første posisjon? Trenger å til den andre linjen legg til den første linjen multiplisert med –2. Mentalt eller på et utkast, multipliser den første linjen med –2: (–2, –4, 2, –18). Og vi utfører konsekvent (igjen mentalt eller på et utkast) tillegg, til den andre linjen legger vi til den første linjen, allerede multiplisert med –2:
Vi skriver resultatet i den andre linjen: 
Vi behandler den tredje linjen på samme måte (3, 2, –5, –1). For å få en null i første posisjon, trenger du til den tredje linjen legg til den første linjen multiplisert med –3. Mentalt eller på et utkast, multipliser den første linjen med –3: (–3, –6, 3, –27). OG til den tredje linjen legger vi den første linjen multiplisert med –3:
Vi skriver resultatet i tredje linje:
I praksis blir disse handlingene vanligvis utført muntlig og skrevet ned i ett trinn: 
Du trenger ikke å telle alt på en gang og samtidig. Rekkefølgen på beregninger og "skriving inn" av resultatene konsistent og vanligvis er det slik: først omskriver vi den første linjen, og puster sakte på oss selv - KONSEKVENT og OPPMERKSOMT:
Og jeg har allerede diskutert den mentale prosessen med selve beregningene ovenfor.
I dette eksemplet er dette enkelt å gjøre; vi deler den andre linjen med –5 (siden alle tallene der er delbare med 5 uten en rest). Samtidig deler vi den tredje linjen med –2, fordi jo mindre tallene er, desto enklere er løsningen:
På sluttstadiet av elementære transformasjoner må du få en annen null her: 
For dette til den tredje linjen legger vi den andre linjen multiplisert med –2:
Prøv å finne ut av denne handlingen selv - multipliser mentalt den andre linjen med –2 og utfør addisjonen.
Den siste handlingen som utføres er frisyren til resultatet, del den tredje linjen med 3.
Som et resultat av elementære transformasjoner ble et ekvivalent system med lineære ligninger oppnådd: 
Kul.
Nå kommer det motsatte av Gauss-metoden inn. Ligningene "slapper av" fra bunn til topp.
I den tredje ligningen har vi allerede et klart resultat:
La oss se på den andre ligningen: . Betydningen av "zet" er allerede kjent, således:
Og til slutt, den første ligningen: . "Igrek" og "zet" er kjent, det er bare et spørsmål om små ting:
Svar: ![]()
Som allerede har blitt bemerket flere ganger, for ethvert ligningssystem er det mulig og nødvendig å sjekke løsningen som er funnet, heldigvis er dette enkelt og raskt.
Eksempel 2

Dette er et eksempel på en uavhengig løsning, et utvalg av det endelige designet og et svar på slutten av leksjonen.
Det skal bemerkes at din fremdriften av vedtaket faller kanskje ikke sammen med min beslutningsprosess, og dette er et trekk ved Gauss-metoden. Men svarene må være de samme!
Eksempel 3
Løs et system med lineære ligninger ved å bruke Gauss-metoden 
La oss skrive ned den utvidede matrisen til systemet og, ved hjelp av elementære transformasjoner, bringe den til en trinnvis form:
Vi ser på øvre venstre "trinn". Vi burde ha en der. Problemet er at det ikke er noen enheter i den første kolonnen i det hele tatt, så omorganisering av radene vil ikke løse noe. I slike tilfeller må enheten organiseres ved hjelp av en elementær transformasjon. Dette kan vanligvis gjøres på flere måter. Jeg gjorde dette:
(1) Til den første linjen legger vi den andre linjen, multiplisert med –1. Det vil si at vi mentalt multipliserte den andre linjen med –1 og la til den første og andre linjen, mens den andre linjen ikke endret seg.

Nå øverst til venstre er det "minus en", noe som passer oss ganske bra. Alle som ønsker å få +1 kan utføre en ekstra bevegelse: multipliser den første linjen med –1 (endre fortegn).
(2) Den første linjen multiplisert med 5 ble lagt til den andre linjen. Den første linjen multiplisert med 3 ble lagt til den tredje linjen.
(3) Den første linjen ble multiplisert med –1, i prinsippet er dette for skjønnhet. Tegnet på den tredje linjen ble også endret og den ble flyttet til andreplass, slik at vi på det andre "trinnet" hadde den nødvendige enheten.
(4) Den andre linjen ble lagt til den tredje linjen, multiplisert med 2.
(5) Den tredje linjen ble delt med 3.
Et dårlig tegn som indikerer en feil i beregninger (sjeldnere, en skrivefeil) er en "dårlig" bunnlinje. Det vil si, hvis vi fikk noe sånt som , nedenfor, og følgelig, ![]() , så kan vi med høy grad av sannsynlighet si at det ble gjort en feil under elementære transformasjoner.
, så kan vi med høy grad av sannsynlighet si at det ble gjort en feil under elementære transformasjoner.
Vi belaster det motsatte, i utformingen av eksempler omskriver de ofte ikke selve systemet, men ligningene er "tatt direkte fra den gitte matrisen." Det omvendte slaget, minner jeg deg om, fungerer fra bunn til topp. Ja, her er en gave:
Svar: ![]() .
.
Eksempel 4
Løs et system med lineære ligninger ved å bruke Gauss-metoden 
Dette er et eksempel for deg å løse på egen hånd, det er noe mer komplisert. Det er greit hvis noen blir forvirret. Full løsning og prøvedesign på slutten av leksjonen. Din løsning kan være forskjellig fra min løsning.
I den siste delen skal vi se på noen funksjoner ved den Gaussiske algoritmen.
Den første funksjonen er at noen ganger mangler noen variabler fra systemligningene, for eksempel: 
Hvordan skrive den utvidede systemmatrisen riktig? Jeg har allerede snakket om dette punktet i klassen. Cramers regel. Matrisemetode. I den utvidede matrisen til systemet setter vi nuller i stedet for manglende variabler: 
Forresten, dette er et ganske enkelt eksempel, siden den første kolonnen allerede har en null, og det er færre elementære transformasjoner å utføre.
Den andre funksjonen er denne. I alle eksemplene som ble vurdert, plasserte vi enten -1 eller +1 på "trinnene". Kan det være andre tall der? I noen tilfeller kan de. Tenk på systemet:  .
.
Her på øvre venstre "trinn" har vi en toer. Men vi legger merke til det faktum at alle tallene i den første kolonnen er delbare med 2 uten en rest - og den andre er to og seks. Og de to øverst til venstre vil passe oss! I det første trinnet må du utføre følgende transformasjoner: legg til den første linjen multiplisert med –1 til den andre linjen; til den tredje linjen legg til den første linjen multiplisert med –3. På denne måten vil vi få de nødvendige nullene i den første kolonnen.
Eller et annet vanlig eksempel:  . Her passer de tre på det andre "trinnet" oss også, siden 12 (stedet der vi må få null) er delelig med 3 uten en rest. Det er nødvendig å utføre følgende transformasjon: legg til den andre linjen til den tredje linjen, multiplisert med -4, som et resultat av at null vi trenger vil bli oppnådd.
. Her passer de tre på det andre "trinnet" oss også, siden 12 (stedet der vi må få null) er delelig med 3 uten en rest. Det er nødvendig å utføre følgende transformasjon: legg til den andre linjen til den tredje linjen, multiplisert med -4, som et resultat av at null vi trenger vil bli oppnådd.
Gauss metode er universell, men det er en særegenhet. Du kan trygt lære å løse systemer ved å bruke andre metoder (Cramers metode, matrisemetode) bokstavelig talt første gang - de har en veldig streng algoritme. Men for å føle deg trygg på den Gaussiske metoden, må du bli god på den og løse minst 5-10 systemer. Derfor kan det i begynnelsen oppstå forvirring og feil i beregninger, og det er ikke noe uvanlig eller tragisk ved dette.
Regnfullt høstvær utenfor vinduet.... Derfor, for alle som ønsker et mer komplekst eksempel å løse på egenhånd:
Eksempel 5
Løs et system med fire lineære ligninger med fire ukjente ved hjelp av Gauss-metoden. 
En slik oppgave er ikke så sjelden i praksis. Jeg tror selv en tekanne som har studert denne siden grundig vil forstå algoritmen for å løse et slikt system intuitivt. I bunn og grunn er alt det samme - det er bare flere handlinger.
Tilfeller hvor systemet ikke har noen løsninger (inkonsekvent) eller har uendelig mange løsninger diskuteres i leksjonen Inkompatible systemer og systemer med felles løsning. Der kan du fikse den betraktede algoritmen til Gauss-metoden.
Jeg ønsker deg suksess!
Løsninger og svar:
Eksempel 2: Løsning: La oss skrive ned den utvidede matrisen til systemet og, ved hjelp av elementære transformasjoner, bringe den til en trinnvis form.

Elementære transformasjoner utført:
(1) Den første linjen ble lagt til den andre linjen, multiplisert med –2. Den første linjen ble lagt til den tredje linjen, multiplisert med –1. Merk følgende! Her kan du bli fristet til å trekke den første fra den tredje linjen; jeg anbefaler på det sterkeste å ikke trekke den fra - risikoen for feil øker betraktelig. Bare brett den!
(2) Tegnet på den andre linjen ble endret (multiplisert med –1). Den andre og tredje linjen er byttet. Merk, at på "trinnene" er vi ikke bare fornøyd med en, men også med –1, som er enda mer praktisk.
(3) Den andre linjen ble lagt til den tredje linjen, multiplisert med 5.
(4) Tegnet på den andre linjen ble endret (multiplisert med –1). Den tredje linjen ble delt med 14.
Omvendt:
Svar: ![]() .
.
Eksempel 4: Løsning: La oss skrive ned den utvidede matrisen til systemet og, ved hjelp av elementære transformasjoner, bringe den til en trinnvis form:

Utførte konverteringer:
(1) En andre linje ble lagt til den første linjen. Dermed er den ønskede enheten organisert på øvre venstre "trinn".
(2) Den første linjen multiplisert med 7 ble lagt til den andre linjen. Den første linjen multiplisert med 6 ble lagt til den tredje linjen.
Med det andre "steget" blir alt verre, "kandidatene" for det er tallene 17 og 23, og vi trenger enten en eller -1. Transformasjoner (3) og (4) vil være rettet mot å oppnå ønsket enhet
(3) Den andre linjen ble lagt til den tredje linjen, multiplisert med –1.
(4) Den tredje linjen ble lagt til den andre linjen, multiplisert med –3.
Det nødvendige elementet på det andre trinnet er mottatt.
.
(5) Den andre linjen ble lagt til den tredje linjen, multiplisert med 6.
Som en del av timene Gaussisk metode Og Inkompatible systemer/systemer med felles løsning vi vurderte inhomogene systemer av lineære ligninger, Hvor gratis medlem(som vanligvis er til høyre) minst en fra ligningene var forskjellig fra null.
Og nå, etter en god oppvarming med matriserangering, vil vi fortsette å polere teknikken elementære transformasjoner på homogent system av lineære ligninger.
Ut fra de første avsnittene kan materialet virke kjedelig og middelmådig, men dette inntrykket er villedende. I tillegg til videreutvikling av teknikker, vil det være mye ny informasjon, så prøv å ikke overse eksemplene i denne artikkelen.
Gaussmetoden, også kalt metoden for sekvensiell eliminering av ukjente, er som følger. Ved å bruke elementære transformasjoner bringes et system av lineære ligninger til en slik form at matrisen av koeffisienter viser seg å være trapesformet (det samme som trekantet eller trinnformet) eller nær trapesformet (direkte slag av Gauss-metoden, heretter ganske enkelt rett slag). Et eksempel på et slikt system og dets løsning er i figuren over.
I et slikt system inneholder den siste ligningen bare én variabel, og verdien kan entydig finnes. Verdien av denne variabelen erstattes deretter med den forrige ligningen ( invers av Gauss-metoden , deretter bare omvendt), hvorfra den forrige variabelen er funnet, og så videre.
I et trapesformet (trekantet) system, som vi ser, inneholder ikke lenger den tredje ligningen variabler y Og x, og den andre ligningen er variabelen x .
Etter at matrisen til systemet har tatt en trapesformet form, er det ikke lenger vanskelig å forstå problemet med kompatibilitet til systemet, bestemme antall løsninger og finne løsningene selv.
Fordeler med metoden:
- når man løser systemer med lineære ligninger med mer enn tre ligninger og ukjente, er ikke Gauss-metoden like tungvint som Cramer-metoden, siden løsning med Gauss-metoden krever færre beregninger;
- Gauss-metoden kan løse ubestemte systemer av lineære ligninger, det vil si å ha en generell løsning (og vi vil analysere dem i denne leksjonen), og ved å bruke Cramer-metoden kan vi bare fastslå at systemet er ubestemt;
- du kan løse systemer med lineære ligninger der antall ukjente ikke er lik antall ligninger (vi vil også analysere dem i denne leksjonen);
- Metoden er basert på grunnskolemetoder - metoden for å erstatte ukjente og metoden for å legge til ligninger, som vi kom inn på i den tilsvarende artikkelen.
For at alle skal forstå med hvilken enkelhet trapesformede (triangulære, trinn) systemer av lineære ligninger løses, presenterer vi en løsning på et slikt system ved hjelp av omvendt bevegelse. En rask løsning på dette systemet ble vist på bildet i begynnelsen av leksjonen.
Eksempel 1. Løs et system med lineære ligninger ved å bruke invers:
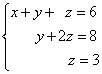
Løsning. I dette trapesformede systemet er variabelen z kan finnes unikt fra den tredje ligningen. Vi erstatter verdien av den i den andre ligningen og får verdien av variabelen y:
Nå vet vi verdiene til to variabler - z Og y. Vi erstatter dem i den første ligningen og får verdien av variabelen x:
Fra de foregående trinnene skriver vi ut løsningen til ligningssystemet:
![]()
For å oppnå et slikt trapesformet system av lineære ligninger, som vi løste veldig enkelt, er det nødvendig å bruke et foroverslag assosiert med elementære transformasjoner av systemet med lineære ligninger. Det er heller ikke veldig vanskelig.
Elementære transformasjoner av et system av lineære ligninger
Ved å gjenta skolemetoden med å algebraisk addere likningene til et system, fant vi ut at til en av likningene i systemet kan vi legge til en annen likning av systemet, og hver av likningene kan multipliseres med noen tall. Som et resultat får vi et system med lineære ligninger som tilsvarer denne. I den inneholdt en ligning allerede bare én variabel, og erstatter verdien av denne med andre ligninger, vi kommer til en løsning. Slik tillegg er en av typene elementær transformasjon av systemet. Ved bruk av Gaussmetoden kan vi bruke flere typer transformasjoner.

Animasjonen ovenfor viser hvordan ligningssystemet gradvis blir til et trapesformet. Det vil si den du så i den aller første animasjonen og overbeviste deg selv om at det er lett å finne verdiene til alle ukjente fra den. Hvordan utføre en slik transformasjon og selvfølgelig eksempler vil bli diskutert videre.
Når du løser systemer av lineære ligninger med et hvilket som helst antall ligninger og ukjente i ligningssystemet og i den utvidede matrisen til systemet Kan:
- omorganisere linjer (dette ble nevnt helt i begynnelsen av denne artikkelen);
- hvis andre transformasjoner resulterer i like eller proporsjonale rader, kan de slettes, bortsett fra én;
- fjern "null" rader der alle koeffisienter er lik null;
- multiplisere eller dele en streng med et visst tall;
- til en hvilken som helst linje legg til en annen linje, multiplisert med et visst tall.
Som et resultat av transformasjonene får vi et system med lineære ligninger som tilsvarer denne.
Algoritme og eksempler på å løse et system av lineære ligninger med en kvadratisk matrise av systemet ved hjelp av Gauss-metoden
La oss først vurdere å løse systemer med lineære ligninger der antall ukjente er lik antall ligninger. Matrisen til et slikt system er kvadratisk, det vil si at antall rader i det er lik antall kolonner.
Eksempel 2. Løs et system med lineære ligninger ved å bruke Gauss-metoden
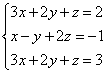
Når vi løste systemer med lineære ligninger ved hjelp av skolemetoder, multipliserte vi en av ligningene termin for ledd med et visst tall, slik at koeffisientene til den første variabelen i de to likningene var motsatte tall. Når man legger til ligninger, elimineres denne variabelen. Gauss-metoden fungerer på samme måte.
For å forenkle utseendet til løsningen la oss lage en utvidet matrise av systemet:

I denne matrisen er koeffisientene til de ukjente plassert til venstre før den vertikale linjen, og de frie leddene er plassert til høyre etter den vertikale linjen.
For å gjøre det enklere å dele koeffisienter for variabler (for å oppnå divisjon etter enhet) La oss bytte den første og andre raden i systemmatrisen. Vi får et system som tilsvarer dette, siden i et system med lineære ligninger kan ligningene byttes ut:

Bruker den nye første ligningen eliminere variabelen x fra den andre og alle påfølgende ligninger. For å gjøre dette legger vi til den andre raden i matrisen den første raden multiplisert med (i vårt tilfelle med ), til den tredje raden - den første raden multiplisert med (i vårt tilfelle med ).
Dette er mulig pga
Hvis det var mer enn tre ligninger i systemet vårt, ville vi måtte legge til alle påfølgende ligninger den første linjen, multiplisert med forholdet mellom de tilsvarende koeffisientene, tatt med et minustegn.
Som et resultat får vi en matrise som tilsvarer dette systemet av et nytt ligningssystem, der alle ligninger, fra den andre inneholder ikke en variabel x :
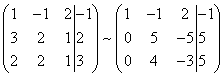
For å forenkle den andre linjen i det resulterende systemet, multipliser den med og få igjen matrisen til et ligningssystem som tilsvarer dette systemet:

Nå, holder den første ligningen til det resulterende systemet uendret, ved å bruke den andre ligningen eliminerer vi variabelen y fra alle påfølgende ligninger. For å gjøre dette legger vi til den tredje raden i systemmatrisen den andre raden, multiplisert med (i vårt tilfelle med ).
Hvis det var mer enn tre ligninger i systemet vårt, ville vi måtte legge til en andre linje til alle påfølgende ligninger, multiplisert med forholdet mellom de tilsvarende koeffisientene tatt med et minustegn.
Som et resultat får vi igjen matrisen til et system som tilsvarer dette systemet med lineære ligninger:
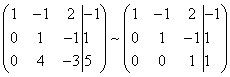
Vi har fått et ekvivalent trapesformet system av lineære ligninger:

Hvis antallet ligninger og variabler er større enn i vårt eksempel, fortsetter prosessen med sekvensiell eliminering av variabler til systemmatrisen blir trapesformet, som i vårt demoeksempel.
Vi vil finne løsningen "fra slutten" - det motsatte trekket. For dette fra den siste ligningen vi bestemmer z:
.
Sette denne verdien inn i forrige ligning, vi finner y:
Fra den første ligningen vi finner x:
![]()
Svar: løsningen på dette ligningssystemet er ![]() .
.
: i dette tilfellet vil det samme svaret bli gitt hvis systemet har en unik løsning. Hvis systemet har et uendelig antall løsninger, vil dette være svaret, og dette er temaet i den femte delen av denne leksjonen.
Løs et system med lineære ligninger ved hjelp av Gaussmetoden selv, og se deretter på løsningen
Her har vi igjen et eksempel på et konsistent og bestemt system av lineære ligninger, der antall ligninger er lik antall ukjente. Forskjellen fra vårt demoeksempel fra algoritmen er at det allerede er fire ligninger og fire ukjente.
Eksempel 4. Løs et system med lineære ligninger ved å bruke Gauss-metoden:


Nå må du bruke den andre ligningen for å eliminere variabelen fra påfølgende ligninger. La oss utføre det forberedende arbeidet. For å gjøre det mer praktisk med forholdet mellom koeffisienter, må du få en i den andre kolonnen i den andre raden. For å gjøre dette, trekk den tredje fra den andre linjen, og multipliser den resulterende andre linjen med -1.
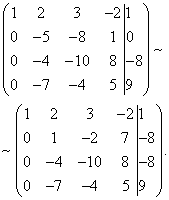
La oss nå utføre den faktiske elimineringen av variabelen fra den tredje og fjerde ligningen. For å gjøre dette, legg til den andre linjen, multiplisert med , til den tredje linjen, og den andre, multiplisert med , til den fjerde linjen.

Nå, ved å bruke den tredje ligningen, eliminerer vi variabelen fra den fjerde ligningen. For å gjøre dette, legg til den tredje linjen til den fjerde linjen, multiplisert med . Vi får en utvidet trapesformet matrise.

Vi fikk et ligningssystem som det gitte systemet er ekvivalent med:

Følgelig er de resulterende og gitte systemene kompatible og bestemte. Vi finner den endelige løsningen "fra slutten". Fra den fjerde ligningen kan vi direkte uttrykke verdien av variabelen "x-fire":
Vi erstatter denne verdien i den tredje ligningen i systemet og får
![]() ,
,
![]() ,
,
Til slutt, verdisubstitusjon
Den første ligningen gir
![]() ,
,
hvor finner vi "x først":
Svar: dette ligningssystemet har en unik løsning ![]() .
.
Du kan også sjekke løsningen til systemet på en kalkulator ved å bruke Cramers metode: i dette tilfellet vil det samme svaret bli gitt hvis systemet har en unik løsning.
Løse anvendte problemer ved hjelp av Gauss-metoden ved å bruke eksempelet på et problem på legeringer
Systemer med lineære ligninger brukes til å modellere virkelige objekter i den fysiske verden. La oss løse ett av disse problemene - legeringer. Lignende problemer er problemer med blandinger, kostnaden eller andelen av individuelle varer i en varegruppe og lignende.
Eksempel 5. Tre stykker legering har en totalmasse på 150 kg. Den første legeringen inneholder 60% kobber, den andre - 30%, den tredje - 10%. Dessuten, i den andre og tredje legeringen samlet er det 28,4 kg mindre kobber enn i den første legeringen, og i den tredje legeringen er det 6,2 kg mindre kobber enn i den andre. Finn massen til hvert stykke av legeringen.
Løsning. Vi lager et system med lineære ligninger:

Vi multipliserer andre og tredje ligning med 10, får vi et ekvivalent system med lineære ligninger:
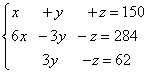
Vi lager en utvidet matrise av systemet:

Oppmerksomhet, rett frem. Ved å legge til (i vårt tilfelle, subtrahere) en rad multiplisert med et tall (vi bruker det to ganger), skjer følgende transformasjoner med den utvidede matrisen til systemet:

Den direkte flyttingen er over. Vi fikk en utvidet trapesformet matrise.
Vi bruker det motsatte trekket. Vi finner løsningen fra slutten. Det ser vi.
Fra den andre ligningen finner vi
Fra den tredje ligningen -
Du kan også sjekke løsningen til systemet på en kalkulator ved å bruke Cramers metode: i dette tilfellet vil det samme svaret bli gitt hvis systemet har en unik løsning.
Enkelheten i Gauss metode bevises av det faktum at det tok den tyske matematikeren Carl Friedrich Gauss bare 15 minutter å finne den opp. I tillegg til metoden oppkalt etter ham, er ordtaket "Vi bør ikke forveksle det som virker utrolig og unaturlig for oss med det absolutt umulige" kjent fra Gauss verk - en slags kort instruksjon om å gjøre funn.
I mange anvendte problemer er det kanskje ikke en tredje begrensning, det vil si en tredje ligning, da må du løse et system med to ligninger med tre ukjente ved hjelp av Gauss-metoden, eller omvendt er det færre ukjente enn ligninger. Vi skal nå begynne å løse slike ligningssystemer.
Ved å bruke Gauss-metoden kan du finne ut om et system er kompatibelt eller inkompatibelt n lineære ligninger med n variabler.
Gauss-metoden og systemer av lineære ligninger med et uendelig antall løsninger
Det neste eksemplet er et konsistent, men ubestemt system av lineære ligninger, det vil si å ha et uendelig antall løsninger.
Etter å ha utført transformasjoner i den utvidede matrisen til systemet (omorganisere rader, multiplisere og dele rader med et visst tall, legge til en annen til en rad), kan rader av skjemaet vises
Hvis i alle ligninger har formen
Frie termer er lik null, dette betyr at systemet er ubestemt, det vil si at det har et uendelig antall løsninger, og ligninger av denne typen er "overflødige", og vi ekskluderer dem fra systemet.
Eksempel 6.
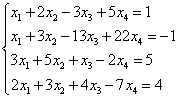
Løsning. La oss lage en utvidet matrise av systemet. Deretter, ved å bruke den første ligningen, eliminerer vi variabelen fra påfølgende ligninger. For å gjøre dette, legg til den andre, tredje og fjerde linjen den første, multiplisert med:

La oss nå legge den andre linjen til den tredje og fjerde.

Som et resultat kommer vi til systemet

De to siste ligningene ble til formlikninger. Disse ligningene er oppfylt for enhver verdi av de ukjente og kan forkastes.
For å tilfredsstille den andre ligningen, kan vi velge vilkårlige verdier for og , da vil verdien for bli bestemt unikt: ![]() . Fra den første ligningen er verdien for også funnet unikt:
. Fra den første ligningen er verdien for også funnet unikt: ![]() .
.
Både det gitte og det siste systemet er konsistente, men usikre, og formlene
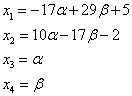
for vilkårlig og gi oss alle løsninger for et gitt system.
Gauss-metoden og systemer av lineære ligninger uten løsninger
Det neste eksempelet er et inkonsekvent system av lineære ligninger, det vil si et som ikke har noen løsninger. Svaret på slike problemer er formulert slik: systemet har ingen løsninger.
Som allerede nevnt i forbindelse med det første eksemplet, etter å ha utført transformasjoner, kan rader av skjemaet vises i den utvidede matrisen til systemet
tilsvarende en ligning av formen
Hvis det blant dem er minst én ligning med en fri term som ikke er null (dvs. ), så er dette ligningssystemet inkonsekvent, det vil si at det ikke har noen løsninger og løsningen er komplett.
Eksempel 7. Løs systemet med lineære ligninger ved å bruke Gauss-metoden:

Løsning. Vi komponerer en utvidet matrise av systemet. Ved å bruke den første ligningen ekskluderer vi variabelen fra påfølgende ligninger. For å gjøre dette, legg til den første linjen multiplisert med til den andre linjen, den første linjen multiplisert med den tredje linjen, og den første linjen multiplisert med den fjerde linjen.

Nå må du bruke den andre ligningen for å eliminere variabelen fra påfølgende ligninger. For å oppnå heltallsforhold av koeffisienter, bytter vi andre og tredje rad i den utvidede matrisen til systemet.

For å ekskludere den tredje og fjerde ligningen legger du den andre multiplisert med , til den tredje linjen, og den andre multiplisert med , til den fjerde linjen.
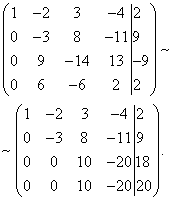
Nå, ved å bruke den tredje ligningen, eliminerer vi variabelen fra den fjerde ligningen. For å gjøre dette, legg til den tredje linjen til den fjerde linjen, multiplisert med .

Det gitte systemet tilsvarer derfor følgende:

Det resulterende systemet er inkonsekvent, siden dets siste ligning ikke kan tilfredsstilles av noen verdier av de ukjente. Derfor har dette systemet ingen løsninger.
I denne leksjonen skal vi se på metoder for å løse et system med lineære ligninger. I et kurs med høyere matematikk kreves det at systemer med lineære ligninger løses både i form av separate oppgaver, for eksempel "Løs systemet ved å bruke Cramers formler," og i løpet av å løse andre problemer. Systemer med lineære ligninger må håndteres i nesten alle grener av høyere matematikk.
Først litt teori. Hva betyr det matematiske ordet "lineær" i dette tilfellet? Dette betyr at likningene til systemet Alle variabler inkludert i første grad: uten noen fancy ting som ![]() osv., som kun deltakere i matematiske olympiader er fornøyd med.
osv., som kun deltakere i matematiske olympiader er fornøyd med.
I høyere matematikk brukes ikke bare bokstaver kjent fra barndommen for å betegne variabler.
Et ganske populært alternativ er variabler med indekser: .
Eller de første bokstavene i det latinske alfabetet, små og store:
Det er ikke så sjeldent å finne greske bokstaver: – kjent for mange som “alfa, beta, gamma”. Og også et sett med indekser, si, med bokstaven "mu":
Bruken av et eller annet sett med bokstaver avhenger av delen av høyere matematikk der vi står overfor et system med lineære ligninger. Så, for eksempel, i systemer med lineære ligninger man møter når man løser integraler og differensialligninger, er det tradisjonelt å bruke notasjonen
Men uansett hvordan variablene er utpekt, endres ikke prinsippene, metodene og metodene for å løse et system med lineære ligninger. Derfor, hvis du kommer over noe skummelt som , ikke skynd deg å lukke problemboken i frykt, tross alt kan du tegne solen i stedet, en fugl i stedet, og et ansikt (læreren) i stedet. Og, hvor morsomt det enn kan virke, kan et system av lineære ligninger med disse notasjonene også løses.
Jeg har en følelse av at artikkelen kommer til å bli ganske lang, så en liten innholdsfortegnelse. Så den sekvensielle "debriefingen" vil være slik:
– Løse et system med lineære ligninger ved å bruke substitusjonsmetoden ("skolemetoden");
– Løsning av systemet ved ledd-for-ledd addisjon (subtraksjon) av systemligningene;
– Løsning av systemet ved hjelp av Cramers formler;
– Løse systemet ved hjelp av en invers matrise;
– Løse systemet ved hjelp av Gauss-metoden.
Alle er kjent med systemer med lineære ligninger fra skolematematikkkurs. I hovedsak starter vi med repetisjon.
Løse et system med lineære ligninger ved hjelp av substitusjonsmetoden
Denne metoden kan også kalles "skolemetoden" eller metoden for å eliminere ukjente. Billedlig talt kan det også kalles "en uferdig gaussisk metode."
Eksempel 1
![]()
Her får vi et system med to likninger med to ukjente. Merk at de frie leddene (nummer 5 og 7) er plassert på venstre side av ligningen. Generelt sett spiller det ingen rolle hvor de er, til venstre eller til høyre, det er bare at i problemer i høyere matematikk er de ofte plassert på den måten. Og et slikt opptak bør ikke føre til forvirring; om nødvendig kan systemet alltid skrives "som vanlig": . Ikke glem at når du flytter et begrep fra del til del, må det endre fortegn.
Hva vil det si å løse et system med lineære ligninger? Å løse et ligningssystem betyr å finne mange av løsningene. Løsningen til et system er et sett med verdier av alle variabler som er inkludert i det, som gjør HVER likning i systemet til en ekte likhet. I tillegg kan systemet være ikke-ledd (har ingen løsninger).Ikke vær sjenert, dette er en generell definisjon =) Vi vil bare ha én «x»-verdi og én «y»-verdi, som tilfredsstiller hver c-we-ligning.
Det finnes en grafisk metode for å løse systemet, som du kan gjøre deg kjent med i timen. De enkleste problemene med en linje. Der snakket jeg om geometrisk sans systemer av to lineære ligninger med to ukjente. Men nå er dette epoken for algebra, og tall-tall, handlinger-handlinger.
La oss bestemme: fra den første ligningen uttrykker vi:
Vi erstatter det resulterende uttrykket i den andre ligningen:
Vi åpner parentesene, legger til lignende termer og finner verdien: 
Deretter husker vi hva vi danset for:
Vi vet allerede verdien, alt som gjenstår er å finne:
Svar:
Etter at NOEN likningssystem er løst på NOEN måte, anbefaler jeg på det sterkeste å sjekke (muntlig, på utkast eller på en kalkulator). Heldigvis gjøres dette enkelt og raskt.
1) Bytt inn det funnet svaret i den første ligningen:
– riktig likestilling oppnås.
2) Bytt inn det funnet svaret i den andre ligningen: ![]()
– riktig likestilling oppnås.
Eller, for å si det enklere, "alt kom sammen"
Den vurderte løsningsmetoden er ikke den eneste; fra den første ligningen var det mulig å uttrykke , og ikke .
Du kan gjøre det motsatte - uttrykke noe fra den andre ligningen og erstatte den med den første ligningen. Merk forresten at den mest uheldige av de fire metodene er å uttrykke fra den andre ligningen:
Resultatet er brøker, men hvorfor? Det finnes en mer rasjonell løsning.
Men i noen tilfeller kan du fortsatt ikke klare deg uten brøker. I denne forbindelse vil jeg gjøre deg oppmerksom på HVORDAN jeg skrev ned uttrykket. Ikke slik: og ikke i noe tilfelle slik: ![]() .
.
Hvis du i høyere matematikk har å gjøre med brøktall, prøv å utføre alle beregninger i vanlige uekte brøker.
Akkurat, og ikke eller!
Et komma kan bare brukes noen ganger, spesielt hvis det er det endelige svaret på et problem, og ingen ytterligere handlinger trenger å utføres med dette nummeret.
Mange lesere tenkte nok "hvorfor en så detaljert forklaring som for en korreksjonsklasse, alt er klart." Ingenting av det slaget, det virker som et så enkelt skoleeksempel, men det er så mange VELDIG viktige konklusjoner! Her er en annen:
Du bør strebe etter å fullføre enhver oppgave på den mest rasjonelle måten. Om ikke annet fordi det sparer tid og nerver, og også reduserer sannsynligheten for å gjøre en feil.
Hvis du i en oppgave i høyere matematikk kommer over et system med to lineære ligninger med to ukjente, så kan du alltid bruke substitusjonsmetoden (med mindre det er indikert at systemet må løses med en annen metode) Ikke en eneste lærer vil tror at du er en sucker og vil redusere karakteren din for å bruke "skolemetoden" "
Dessuten er det i noen tilfeller tilrådelig å bruke substitusjonsmetoden med et større antall variabler.
Eksempel 2
Løs et system med lineære ligninger med tre ukjente

Et lignende ligningssystem oppstår ofte ved bruk av den såkalte metoden med ubestemte koeffisienter, når vi finner integralet til en rasjonell brøkfunksjon. Det aktuelle systemet ble tatt derfra av meg.
Når man skal finne integralet er målet fort finn verdiene til koeffisientene, i stedet for å bruke Cramers formler, den inverse matrisemetoden, etc. Derfor, i dette tilfellet, er substitusjonsmetoden passende.
Når et hvilket som helst ligningssystem er gitt, er det først og fremst ønskelig å finne ut om det er mulig på en eller annen måte å forenkle det UMIDDELBART? Ved å analysere likningene til systemet legger vi merke til at den andre likningen i systemet kan deles på 2, som er det vi gjør:

Henvisning: det matematiske tegnet betyr «av dette følger at» og brukes ofte i problemløsning.
La oss nå analysere ligningene; vi må uttrykke en variabel i form av de andre. Hvilken ligning skal jeg velge? Du har sikkert allerede gjettet at den enkleste måten for dette formålet er å ta den første ligningen av systemet:

Her, uansett hvilken variabel man skal uttrykke, kunne man like gjerne uttrykke eller .
Deretter erstatter vi uttrykket i den andre og tredje likningen av systemet: 
Vi åpner parentesene og presenterer lignende termer: 
Del den tredje ligningen med 2: 
Fra den andre ligningen uttrykker og erstatter vi inn i den tredje ligningen:

Nesten alt er klart, fra den tredje ligningen finner vi:
Fra den andre ligningen: ![]()
Fra den første ligningen:
Sjekk: Bytt inn de funnet verdiene til variablene på venstre side av hver ligning i systemet:
1)
2)
3)
De korresponderende høyresidene av ligningene oppnås, og dermed er løsningen funnet riktig.
Eksempel 3
Løs et system av lineære ligninger med 4 ukjente

Dette er et eksempel du kan løse på egen hånd (svar på slutten av leksjonen).
Løsning av systemet ved å legge til (subtraksjon) ledd for ledd av systemlikningene
Når du løser systemer med lineære ligninger, bør du prøve å ikke bruke "skolemetoden", men metoden for termin-for-ledd addisjon (subtraksjon) av likningene til systemet. Hvorfor? Dette sparer tid og forenkler beregninger, men nå vil alt bli klarere.
Eksempel 4
Løs et system med lineære ligninger: ![]()
Jeg tok samme system som i det første eksemplet.
Ved å analysere ligningssystemet legger vi merke til at koeffisientene til variabelen er identiske i størrelse og motsatte i fortegn (–1 og 1). I en slik situasjon kan ligningene legges til ledd for ledd: 
Handlinger sirklet i rødt utføres MENTALT.
Som du kan se, som et resultat av termin-for-term addisjon, mistet vi variabelen. Dette er faktisk hva essensen av metoden er å kvitte seg med en av variablene.
§1. Systemer av lineære ligninger.
Vis system
kalt et system m lineære ligninger med n ukjent.
Her  - ukjent,
- ukjent,  - koeffisienter for ukjente,
- koeffisienter for ukjente,  - frie termer av ligningene.
- frie termer av ligningene.
Hvis alle frie ledd i ligningene er lik null, kalles systemet homogen.Ved avgjørelse systemet kalles en samling av tall  , når de erstattes med systemet i stedet for ukjente, blir alle ligninger til identiteter. Systemet kalles ledd, hvis den har minst én løsning. Et kompatibelt system som har en unik løsning kalles sikker. De to systemene kalles tilsvarende, hvis settene med løsningene deres faller sammen.
, når de erstattes med systemet i stedet for ukjente, blir alle ligninger til identiteter. Systemet kalles ledd, hvis den har minst én løsning. Et kompatibelt system som har en unik løsning kalles sikker. De to systemene kalles tilsvarende, hvis settene med løsningene deres faller sammen.
System (1) kan representeres i matriseform ved å bruke ligningen
 (2)
(2)
 .
.
§2. Kompatibilitet av systemer med lineære ligninger.
La oss kalle den utvidede matrisen til system (1) matrisen

Kronecker-Capelli teorem. System (1) er konsistent hvis og bare hvis rangeringen til systemmatrisen er lik rangeringen til den utvidede matrisen:
 .
.
§3. Systemløsningn lineære ligninger medn ukjent.
Tenk på et inhomogent system n lineære ligninger med n ukjent:
 (3)
(3)
Cramers teorem.Hvis hoveddeterminanten for systemet (3)  , så har systemet en unik løsning, bestemt av formlene:
, så har systemet en unik løsning, bestemt av formlene:

de.  ,
,
Hvor  - determinant hentet fra determinanten
- determinant hentet fra determinanten  erstatning
erstatning  kolonne til kolonnen med gratis medlemmer.
kolonne til kolonnen med gratis medlemmer.
Hvis  , og minst én av
, og minst én av  ≠0, da har systemet ingen løsninger.
≠0, da har systemet ingen løsninger.
Hvis  , så har systemet uendelig mange løsninger.
, så har systemet uendelig mange løsninger.
System (3) kan løses ved å bruke sin matriseform (2). Hvis matrisen rangerer EN er lik n, dvs.  , deretter matrisen EN har en invers
, deretter matrisen EN har en invers  . Multiplisere matriseligningen
. Multiplisere matriseligningen  til matrisen
til matrisen  til venstre får vi:
til venstre får vi:
 .
.
Den siste likheten uttrykker metoden for å løse systemer av lineære ligninger ved å bruke en invers matrise.
Eksempel. Løs et ligningssystem ved å bruke en invers matrise.

Løsning.
Matrise  ikke-degenerert, siden
ikke-degenerert, siden  , som betyr at det er en invers matrise. La oss beregne den inverse matrisen:
, som betyr at det er en invers matrise. La oss beregne den inverse matrisen:  .
.

 ,
,
Trening. Løs systemet ved å bruke Cramers metode.
§4. Løse vilkårlige systemer av lineære ligninger.
La et ikke-homogent system av lineære ligninger av formen (1) gis.
La oss anta at systemet er konsistent, dvs. betingelsen for Kronecker-Capelli-teoremet er oppfylt:  . Hvis matrisen rangerer
. Hvis matrisen rangerer  (antall ukjente), så har systemet en unik løsning. Hvis
(antall ukjente), så har systemet en unik løsning. Hvis  , så har systemet uendelig mange løsninger. La meg forklare.
, så har systemet uendelig mange løsninger. La meg forklare.
La rangeringen av matrisen r(EN)=
r<
n. Fordi det  , så er det et eller annet moll som ikke er null r. La oss kalle det grunnleggende mindre. De ukjente hvis koeffisienter utgjør en basis-minor vil bli kalt grunnleggende variabler. Vi kaller de resterende ukjente for frie variabler. La oss omorganisere ligningene og omnummerere variablene slik at denne mindre er plassert i øvre venstre hjørne av systemmatrisen:
, så er det et eller annet moll som ikke er null r. La oss kalle det grunnleggende mindre. De ukjente hvis koeffisienter utgjør en basis-minor vil bli kalt grunnleggende variabler. Vi kaller de resterende ukjente for frie variabler. La oss omorganisere ligningene og omnummerere variablene slik at denne mindre er plassert i øvre venstre hjørne av systemmatrisen:
 .
.
Først r linjer er lineært uavhengige, resten uttrykkes gjennom dem. Derfor kan disse linjene (ligningene) forkastes. Vi får:

La oss gi de frie variablene vilkårlige numeriske verdier: . La oss bare la de grunnleggende variablene være på venstre side og flytte de frie til høyre side.

Fikk systemet r lineære ligninger med r ukjent, hvis determinant er forskjellig fra 0. Den har en unik løsning.

Dette systemet kalles den generelle løsningen av systemet med lineære ligninger (1). Ellers: uttrykket av grunnleggende variabler gjennom frie kalles generelt vedtak systemer. Fra den kan du få et uendelig antall private løsninger, og gir frie variabler vilkårlige verdier. En spesiell løsning oppnådd fra en generell løsning for nullverdier av frie variabler kalles grunnleggende løsning. Antallet ulike basisløsninger overskrider ikke  . En grunnleggende løsning med ikke-negative komponenter kalles støttende systemløsning.
. En grunnleggende løsning med ikke-negative komponenter kalles støttende systemløsning.
Eksempel.
 ,r=2.
,r=2.
Variabler  - grunnleggende,
- grunnleggende,  - gratis.
- gratis.
La oss legge sammen ligningene; la oss uttrykke  gjennom
gjennom  :
:
 - felles vedtak.
- felles vedtak.
 - privat løsning for
- privat løsning for  .
.
 - grunnløsning, referanse.
- grunnløsning, referanse.
§5. Gauss metode.
Gauss-metoden er en universell metode for å studere og løse vilkårlige systemer av lineære ligninger. Det består i å redusere systemet til en diagonal (eller trekantet) form ved å sekvensielt eliminere ukjente ved å bruke elementære transformasjoner som ikke bryter med ekvivalensen til systemene. En variabel regnes som ekskludert hvis den er inneholdt i bare én ligning av systemet med en koeffisient på 1.
Elementære transformasjoner systemene er:
Multiplisere en ligning med et annet tall enn null;
Legge til en ligning multiplisert med et hvilket som helst tall med en annen ligning;
Omorganisere ligninger;
Forkaster ligningen 0 = 0.
Elementære transformasjoner kan utføres ikke på ligninger, men på utvidede matriser av de resulterende ekvivalente systemene.
Eksempel.

Løsning. La oss skrive ned den utvidede matrisen til systemet:
 .
.
Ved å utføre elementære transformasjoner vil vi redusere venstre side av matrisen til enhetsform: vi vil lage ener på hoveddiagonalen, og nuller utenfor den.











Kommentar. Hvis, når du utfører elementære transformasjoner, oppnås en ligning på formen 0 = k(Hvor Til 0),
da er systemet inkonsekvent.
0),
da er systemet inkonsekvent.
Løsningen av systemer med lineære ligninger ved hjelp av metoden for sekvensiell eliminering av ukjente kan skrives i formen tabeller.
Den venstre kolonnen i tabellen inneholder informasjon om ekskluderte (grunnleggende) variabler. De resterende kolonnene inneholder koeffisientene til de ukjente og de frie leddene til ligningene.
Den utvidede matrisen til systemet er registrert i kildetabellen. Deretter begynner vi å utføre Jordan-transformasjoner:
1. Velg en variabel  , som vil bli grunnlaget. Den tilsvarende kolonnen kalles nøkkelkolonnen. Velg en ligning der denne variabelen vil forbli, utelukket fra andre ligninger. Den tilsvarende tabellraden kalles en nøkkelrad. Koeffisient
, som vil bli grunnlaget. Den tilsvarende kolonnen kalles nøkkelkolonnen. Velg en ligning der denne variabelen vil forbli, utelukket fra andre ligninger. Den tilsvarende tabellraden kalles en nøkkelrad. Koeffisient  , som står i skjæringspunktet mellom en nøkkelrad og en nøkkelkolonne, kalles en nøkkel.
, som står i skjæringspunktet mellom en nøkkelrad og en nøkkelkolonne, kalles en nøkkel.
2. Nøkkelstrengelementene er delt inn i nøkkelelementet.
3. Nøkkelkolonnen er fylt med nuller.
4. De resterende elementene beregnes ved hjelp av rektangelregelen. Lag et rektangel, i motsatte hjørner som det er et nøkkelelement og et omregnet element; fra produktet av elementene som ligger på diagonalen til rektangelet med nøkkelelementet, trekkes produktet av elementene i den andre diagonalen, og den resulterende forskjellen deles på nøkkelelementet.
Eksempel. Finn den generelle løsningen og grunnleggende løsningen av ligningssystemet:

Løsning.
|
|
|
|
|
|
|
|
|
| ||||||
|
| ||||||
|
|
Generell løsning av systemet:

Grunnleggende løsning:  .
.
En enkelt substitusjonstransformasjon lar deg flytte fra en basis av systemet til en annen: i stedet for en av hovedvariablene, introduseres en av de frie variablene i basisen. For å gjøre dette, velg et nøkkelelement i den frie variabelkolonnen og utfør transformasjoner i henhold til algoritmen ovenfor.
§6. Finne støtteløsninger
Referanseløsningen til et system med lineære ligninger er en grunnleggende løsning som ikke inneholder negative komponenter.
Referanseløsningene til systemet er funnet ved Gauss-metoden når følgende betingelser er oppfylt.
1. I det opprinnelige systemet må alle gratisvilkår være ikke-negative:  .
.
2. Nøkkelelementet er valgt blant de positive koeffisientene.
3. Hvis en variabel introdusert i grunnlaget har flere positive koeffisienter, så er nøkkellinjen den der forholdet mellom frileddet og den positive koeffisienten er minst.
Merknad 1. Hvis, i prosessen med å eliminere ukjente, vises en ligning der alle koeffisientene er ikke-positive og frileddet  , så har systemet ingen ikke-negative løsninger.
, så har systemet ingen ikke-negative løsninger.
Notat 2. Hvis det ikke er et enkelt positivt element i kolonnene med koeffisienter for frie variabler, er overgang til en annen referanseløsning umulig.
Eksempel.

|
|
|














