Tìm giá trị riêng và giá trị riêng của ví dụ ma trận. Phương trình đặc tính ma trận

HỆ THỐNG THIẾT BỊ TUYẾN TÍNH HOMOGENEOUS

Hệ phương trình tuyến tính thuần nhất là hệ có dạng

Rõ ràng là trong trường hợp này , tại vì tất cả các phần tử của một trong các cột trong các yếu tố quyết định này đều bằng không.

Vì các ẩn số được tìm thấy bởi các công thức , thì trong trường hợp Δ ≠ 0, hệ có nghiệm 0 duy nhất x = y = z= 0. Tuy nhiên, trong nhiều bài toán, câu hỏi liệu một hệ thuần nhất có các nghiệm khác 0 hay không được quan tâm.

Định lý.Để hệ phương trình thuần nhất tuyến tính có nghiệm khác dấu thì cần và đủ Δ ≠ 0.

Vì vậy, nếu định thức là Δ ≠ 0 thì hệ có nghiệm duy nhất. Nếu Δ ≠ 0 thì hệ phương trình tuyến tính thuần nhất có vô số nghiệm.

Các ví dụ.

Eigenvectors và Matrix Eigenvalues

Cho một ma trận vuông được , X là một số cột ma trận có chiều cao trùng với thứ tự của ma trận MỘT. .

Trong nhiều bài toán, người ta phải xem xét phương trình X

trong đó λ là một số. Rõ ràng là với bất kỳ λ phương trình này có nghiệm bằng không.

Số λ mà phương trình này có nghiệm khác được gọi là giá trị riêng ma trận MỘT, Nhưng Xđối với λ như vậy được gọi là vector riêng ma trận MỘT.

Hãy cùng tìm ký hiệu riêng của ma trận MỘT. Trong chừng mực E∙X = X, sau đó phương trình ma trận có thể được viết lại thành hoặc . Ở dạng khai triển, phương trình này có thể được viết lại dưới dạng một hệ phương trình tuyến tính. Có thật không .

Và do đó

Vì vậy, chúng tôi có một hệ phương trình tuyến tính thuần nhất để xác định tọa độ x 1, x2, x 3 vectơ X. Để hệ thống có các nghiệm khác không, cần và đủ rằng định thức của hệ thống bằng 0, tức là

Đây là phương trình bậc 3 đối với λ. Nó được gọi là phương trình đặc trưng ma trận MỘT và dùng để xác định các giá trị riêng λ.

Mỗi eigenvalue λ tương ứng với một eigenvector X, có tọa độ được xác định từ hệ thống với giá trị tương ứng của λ.

Các ví dụ.

ĐẠI SỐ VECTOR. KHÁI NIỆM VỀ VECTOR

Khi nghiên cứu các nhánh vật lý khác nhau, có những đại lượng hoàn toàn được xác định bằng cách đặt các giá trị số của chúng, ví dụ, chiều dài, diện tích, khối lượng, nhiệt độ, v.v. Các giá trị như vậy được gọi là vô hướng. Tuy nhiên, bên cạnh chúng còn có các đại lượng, để xác định được thì ngoài trị số còn phải biết phương của chúng trong không gian, ví dụ lực tác dụng lên vật, vận tốc và gia tốc. của vật thể khi nó chuyển động trong không gian, cường độ từ trường tại một điểm nhất định trong không gian và v.v. Các đại lượng như vậy được gọi là đại lượng vectơ.

Hãy để chúng tôi giới thiệu một định nghĩa chặt chẽ.

Phân đoạn định hướng Hãy gọi một phân đoạn, liên quan đến các phần cuối của nó mà nó được biết trong số chúng là đoạn đầu tiên và đoạn nào là đoạn thứ hai.

Véc tơ một phân đoạn có hướng được gọi, có độ dài nhất định, tức là Đây là một đoạn có độ dài nhất định, trong đó một trong những điểm giới hạn nó được coi là điểm đầu và điểm thứ hai - là điểm cuối. Nếu MỘT là phần đầu của vectơ, B là kết thúc của nó, khi đó vectơ được ký hiệu bằng ký hiệu, ngoài ra, vectơ thường được ký hiệu bằng một chữ cái duy nhất. Trong hình, vectơ được biểu thị bằng một đoạn và hướng của nó bằng một mũi tên.

mô-đun hoặc Dài vectơ được gọi là độ dài của đoạn thẳng xác định nó. Ký hiệu bởi || hoặc ||.

Cái gọi là vectơ không, có đầu và cuối trùng nhau, cũng sẽ được gọi là vectơ. Nó được đánh dấu. Vectơ 0 không có hướng xác định và môđun của nó bằng không || = 0.

Vectơ và được gọi là thẳng hàng nếu chúng nằm trên cùng một đường thẳng hoặc trên các đường thẳng song song. Trong trường hợp này, nếu các vectơ và hướng bằng nhau, chúng ta sẽ viết ngược lại.

Các vectơ nằm trên các đường thẳng song song với cùng một mặt phẳng được gọi là đồng phẳng.

Hai vectơ và được gọi là công bằng nếu chúng thẳng hàng, có cùng hướng và có độ dài bằng nhau. Trong trường hợp này, hãy viết.

Từ định nghĩa về đẳng thức của vectơ mà một vectơ có thể di chuyển song song với chính nó bằng cách đặt gốc của nó tại một điểm bất kỳ trong không gian.

Ví dụ.

VẬN HÀNH TUYẾN TÍNH TRÊN vectơ

1. Nhân một vectơ với một số.

   Tích của một vectơ với một số λ là một vectơ mới sao cho:

   Tích của một vectơ và một số λ được ký hiệu là.

   

   Ví dụ, là một vectơ chỉ cùng hướng với vectơ và có độ dài bằng nửa độ dài của vectơ.

   Hoạt động đã nhập có những điều sau đây tính chất:

2. Phép cộng vectơ.

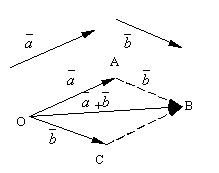
   Cho và là hai vectơ tùy ý. Lấy một điểm tùy ý O và xây dựng một vectơ. Sau đó, từ điểm MỘTđặt véc tơ sang một bên. Vectơ nối điểm đầu của vectơ thứ nhất với điểm cuối của vectơ thứ hai được gọi là Tổng trong số các vectơ này và được ký hiệu là .

   

   Định nghĩa công thức của phép cộng vectơ được gọi là quy tắc hình bình hành, vì tổng các vectơ giống nhau có thể nhận được như sau. Đặt ngoài vấn đề O vectơ và. Dựng một hình bình hành trên các vectơ này OABC. Vì vectơ, thì vectơ, là đường chéo của hình bình hành được vẽ từ đỉnh O, rõ ràng sẽ là tổng của các vectơ.

   

   Thật dễ dàng để kiểm tra những điều sau thuộc tính cộng vectơ.

3. Hiệu của vectơ.

   Một vectơ thẳng hàng với một vectơ đã cho, có độ dài bằng nhau và có hướng ngược nhau, được gọi là đối diện vectơ đối với một vectơ và được ký hiệu là. Vectơ đối có thể được coi là kết quả của phép nhân vectơ với số λ = –1 :.

Làm thế nào để chèn các công thức toán học trên trang web?

Nếu bạn cần thêm một hoặc hai công thức toán học vào trang web, thì cách dễ nhất để thực hiện việc này như được mô tả trong bài viết: các công thức toán học dễ dàng được chèn vào trang web dưới dạng hình ảnh mà Wolfram Alpha tự động tạo ra. Ngoài sự đơn giản, phương pháp phổ quát này sẽ giúp cải thiện khả năng hiển thị của trang web trong các công cụ tìm kiếm. Nó đã hoạt động trong một thời gian dài (và tôi nghĩ rằng nó sẽ hoạt động mãi mãi), nhưng nó đã lỗi thời về mặt đạo đức.

Tuy nhiên, nếu bạn liên tục sử dụng các công thức toán học trên trang web của mình, thì tôi khuyên bạn nên sử dụng MathJax, một thư viện JavaScript đặc biệt hiển thị ký hiệu toán học trong trình duyệt web sử dụng đánh dấu MathML, LaTeX hoặc ASCIIMathML.

Có hai cách để bắt đầu sử dụng MathJax: (1) sử dụng mã đơn giản, bạn có thể nhanh chóng kết nối tập lệnh MathJax với trang web của mình, tập lệnh này sẽ được tự động tải từ máy chủ từ xa vào đúng thời điểm (danh sách các máy chủ); (2) tải tập lệnh MathJax từ máy chủ từ xa lên máy chủ của bạn và kết nối nó với tất cả các trang trên trang web của bạn. Phương pháp thứ hai phức tạp hơn và tốn thời gian hơn và sẽ cho phép bạn tăng tốc tải các trang trên trang web của mình và nếu máy chủ MathJax mẹ tạm thời không khả dụng vì lý do nào đó, điều này sẽ không ảnh hưởng đến trang web của bạn theo bất kỳ cách nào. Mặc dù có những ưu điểm này, tôi đã chọn phương pháp đầu tiên, vì nó đơn giản hơn, nhanh hơn và không đòi hỏi kỹ năng kỹ thuật. Hãy làm theo ví dụ của tôi, và trong vòng 5 phút, bạn sẽ có thể sử dụng tất cả các tính năng của MathJax trên trang web của mình.

Bạn có thể kết nối tập lệnh thư viện MathJax từ một máy chủ từ xa bằng hai tùy chọn mã được lấy từ trang web MathJax chính hoặc từ trang tài liệu:

Một trong những tùy chọn mã này cần được sao chép và dán vào mã của trang web của bạn, tốt nhất là giữa các thẻ Và hoặc ngay sau thẻ . Theo tùy chọn đầu tiên, MathJax tải nhanh hơn và làm chậm trang ít hơn. Nhưng tùy chọn thứ hai sẽ tự động theo dõi và tải các phiên bản mới nhất của MathJax. Nếu bạn chèn mã đầu tiên, thì nó sẽ cần được cập nhật định kỳ. Nếu bạn dán mã thứ hai, thì các trang sẽ tải chậm hơn, nhưng bạn sẽ không cần phải liên tục theo dõi các bản cập nhật của MathJax.

Cách dễ nhất để kết nối MathJax là trong Blogger hoặc WordPress: trong bảng điều khiển trang web, thêm tiện ích con được thiết kế để chèn mã JavaScript của bên thứ ba, sao chép phiên bản đầu tiên hoặc thứ hai của mã tải được trình bày ở trên vào đó và đặt tiện ích con gần hơn ở đầu mẫu (nhân tiện, điều này không cần thiết, vì tập lệnh MathJax được tải không đồng bộ). Đó là tất cả. Bây giờ hãy học cú pháp đánh dấu MathML, LaTeX và ASCIIMathML và bạn đã sẵn sàng để nhúng các công thức toán học vào các trang web của mình.

Fractal nào cũng được xây dựng theo một quy tắc nhất định, được áp dụng nhất quán không giới hạn số lần. Mỗi lần như vậy được gọi là một lần lặp.

Thuật toán lặp lại để xây dựng một miếng bọt biển Menger khá đơn giản: hình lập phương ban đầu có cạnh 1 được chia bởi các mặt phẳng song song với các mặt của nó thành 27 hình lập phương bằng nhau. Một khối ở giữa và 6 khối liền kề với nó dọc theo các mặt được loại bỏ khỏi nó. Nó chỉ ra một tập hợp bao gồm 20 hình khối nhỏ hơn còn lại. Làm tương tự với mỗi hình lập phương này, ta được một tập hợp gồm 400 hình lập phương nhỏ hơn. Tiếp tục quá trình này vô thời hạn, chúng ta nhận được miếng bọt biển Menger.

Hiệu riêng của ma trận vuông là một ký hiệu mà khi nhân với một ma trận đã cho, sẽ cho kết quả là một vectơ thẳng hàng. Nói một cách dễ hiểu, khi một ma trận được nhân với một ký hiệu riêng, thì ma trận vẫn giữ nguyên, nhưng được nhân với một số nào đó.

Sự định nghĩa

Một ký hiệu riêng là một vectơ khác không V, khi nhân với ma trận vuông M, nó sẽ trở thành chính nó, tăng lên một số λ. Trong ký hiệu đại số, điều này trông giống như:

M × V = λ × V,

trong đó λ là một giá trị riêng của ma trận M.

Hãy xem xét một ví dụ số. Để tiện cho việc viết, các số trong ma trận sẽ được phân cách bằng dấu chấm phẩy. Giả sử chúng ta có một ma trận:

• M = 0; 4;
• 6; 10.

Hãy nhân nó với một vectơ cột:

• V = -2;

Khi nhân một ma trận với một vectơ cột, chúng ta cũng nhận được một vectơ cột. Trong ngôn ngữ toán học chặt chẽ, công thức nhân ma trận 2 × 2 với một vectơ cột sẽ có dạng như sau:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 có nghĩa là phần tử của ma trận M, đứng ở hàng đầu tiên và cột đầu tiên, và M22 - phần tử nằm ở hàng thứ hai và cột thứ hai. Đối với ma trận của chúng ta, các phần tử này là M11 = 0, M12 = 4, M21 = 6, M22 10. Đối với vectơ cột, các giá trị này là V11 = –2, V21 = 1. Theo công thức này, chúng ta nhận được như sau kết quả của tích của một ma trận vuông với một vectơ:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Để thuận tiện, chúng ta viết vector cột thành một hàng. Vì vậy, chúng tôi đã nhân ma trận vuông với vectơ (-2; 1), kết quả là vectơ (4; -2). Rõ ràng, đây là cùng một vectơ nhân với λ = -2. Lambda trong trường hợp này biểu thị một giá trị riêng của ma trận.

Ký hiệu riêng của ma trận là một vectơ thẳng hàng, nghĩa là, một đối tượng không thay đổi vị trí của nó trong không gian khi nó được nhân với một ma trận. Khái niệm thẳng hàng trong đại số vectơ tương tự như thuật ngữ song song trong hình học. Trong giải thích hình học, vectơ thẳng hàng là các đoạn thẳng song song có độ dài khác nhau. Kể từ thời Euclid, chúng ta biết rằng một đường thẳng có vô số đường thẳng song song với nó, do đó, hợp lý khi giả sử rằng mỗi ma trận có vô số các eigenvector.

Từ ví dụ trước, có thể thấy rằng cả (-8; 4) và (16; -8) và (32, -16) đều có thể là các eigenvector. Tất cả đều là các vectơ thẳng hàng tương ứng với giá trị riêng λ = -2. Khi nhân ma trận ban đầu với các vectơ này, kết quả là chúng ta vẫn nhận được một vectơ khác với vectơ ban đầu 2 lần. Đó là lý do tại sao, khi giải các bài toán tìm một ký hiệu riêng, yêu cầu chỉ tìm các đối tượng vectơ độc lập tuyến tính. Thông thường, đối với một ma trận n × n, có số thứ n các ký tự riêng. Máy tính của chúng tôi được thiết kế để phân tích ma trận vuông bậc hai, vì vậy hầu như luôn luôn tìm thấy hai ký hiệu riêng, ngoại trừ trường hợp chúng trùng nhau.

Trong ví dụ trên, chúng ta đã biết trước ký tự riêng của ma trận gốc và xác định trực quan số lambda. Tuy nhiên, trong thực tế, mọi thứ diễn ra theo chiều ngược lại: lúc đầu có các giá trị riêng và chỉ sau đó là các giá trị riêng.

Giải thuật giải thuật

Hãy nhìn lại ma trận ban đầu M và cố gắng tìm cả hai ký tự riêng của nó. Vì vậy, ma trận trông giống như:

• M = 0; 4;
• 6; 10.

Để bắt đầu, chúng ta cần xác định giá trị riêng λ, mà chúng ta cần tính định thức của ma trận sau:

• (0 - λ); 4;
• Số 6; (10 - λ).

Ma trận này thu được bằng cách lấy các phần tử trên đường chéo chính trừ đi λ chưa biết. Yếu tố quyết định được xác định theo công thức chuẩn:

• detA = M11 × M21 - M12 × M22
• detA = (0 - λ) × (10 - λ) - 24

Vì vectơ của chúng ta không được bằng 0, chúng ta coi phương trình kết quả là phụ thuộc tuyến tính và cân bằng detA định thức của chúng ta bằng 0.

(0 - λ) × (10 - λ) - 24 = 0

Hãy mở dấu ngoặc và nhận được phương trình đặc trưng của ma trận:

λ 2 - 10λ - 24 = 0

Đây là một phương trình bậc hai tiêu chuẩn cần được giải về mặt phân biệt.

D \ u003d b 2 - 4ac \ u003d (-10) × 2 - 4 × (-1) × 24 \ u003d 100 + 96 \ u003d 196

Gốc của số phân biệt là sqrt (D) = 14, do đó λ1 = -2, λ2 = 12. Bây giờ với mỗi giá trị lambda, chúng ta cần tìm một ký hiệu riêng. Hãy để chúng tôi biểu diễn các hệ số của hệ thống cho λ = -2.

• M - λ × E = 2; 4;
• 6; 12.

Trong công thức này, E là ma trận nhận dạng. Dựa vào ma trận thu được, ta lập hệ phương trình tuyến tính:

2x + 4y = 6x + 12y

trong đó x và y là các phần tử của eigenvector.

Hãy thu thập tất cả chữ X ở bên trái và tất cả chữ Y ở bên phải. Rõ ràng - 4x = 8y. Chia biểu thức cho - 4 và được x = -2y. Bây giờ chúng ta có thể xác định eigenvector đầu tiên của ma trận bằng cách lấy bất kỳ giá trị nào của ẩn số (hãy nhớ về tính vô hạn của eigenvector phụ thuộc tuyến tính). Lấy y = 1 thì x = -2. Do đó, ký tự đầu tiên trông giống như V1 = (–2; 1). Trở lại phần đầu của bài viết. Chính đối tượng vectơ này mà chúng tôi đã nhân ma trận để chứng minh khái niệm về một eigenvector.

Bây giờ chúng ta hãy tìm eigenvector cho λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Chúng ta hãy soạn cùng một hệ phương trình tuyến tính;

• -12x + 4y = 6x - 2y
• -18x = -6y
• 3x = y.

Bây giờ chúng ta hãy lấy x = 1, do đó y = 3. Như vậy, ký hiệu thứ hai trông giống như V2 = (1; 3). Khi nhân ma trận ban đầu với vectơ này, kết quả sẽ luôn là vectơ giống nhân với 12. Điều này hoàn thành thuật toán giải. Bây giờ bạn biết cách xác định thủ công một ký tự riêng của ma trận.

• bản ngã;
• dấu vết, nghĩa là tổng các phần tử trên đường chéo chính;
• xếp hạng, tức là số lượng hàng / cột độc lập tuyến tính tối đa.

Chương trình hoạt động theo thuật toán trên, giảm thiểu quá trình giải. Điều quan trọng là chỉ ra rằng trong chương trình lambda được ký hiệu bằng chữ "c". Hãy xem một ví dụ số.

Ví dụ chương trình

Hãy thử xác định các eigenvectors cho ma trận sau:

• M = 5; 13;
• 4; 14.

Hãy nhập các giá trị này vào các ô của máy tính và nhận được câu trả lời ở dạng sau:

• Hạng ma trận: 2;
• Định thức ma trận: 18;
• Dấu vết ma trận: 19;
• Tính toán Eigenvector: c 2 - 19,00c + 18,00 (phương trình đặc trưng);
• Phép tính Eigenvector: 18 (giá trị lambda đầu tiên);
• Phép tính Eigenvector: 1 (giá trị lambda thứ hai);
• Hệ phương trình của vectơ 1: -13x1 + 13y1 = 4x1 - 4y1;
• Hệ phương trình vectơ 2: 4x1 + 13y1 = 4x1 + 13y1;
• Bộ ký hiệu 1: (1; 1);
• Bộ ký hiệu 2: (-3,25; 1).

Như vậy, chúng ta đã thu được hai eigenvector độc lập tuyến tính.

Phần kết luận

Đại số tuyến tính và hình học giải tích là các môn học tiêu chuẩn cho bất kỳ sinh viên năm nhất nào trong ngành kỹ thuật. Một số lượng lớn các vectơ và ma trận là đáng kinh ngạc, và rất dễ mắc sai lầm trong các phép tính rườm rà như vậy. Chương trình của chúng tôi sẽ cho phép học sinh kiểm tra các phép tính của mình hoặc tự động giải bài toán tìm dấu hiệu riêng. Có những máy tính đại số tuyến tính khác trong danh mục của chúng tôi, hãy sử dụng chúng trong học tập hoặc công việc của bạn.

Với ma trận A, nếu tồn tại số l sao cho AX = lX.

Trong trường hợp này, số l được gọi là giá trị riêng toán tử (ma trận A) tương ứng với vectơ X.

Nói cách khác, eigenvector là một vectơ, dưới tác động của toán tử tuyến tính, biến đổi thành một vectơ thẳng hàng, tức là chỉ nhân với một số. Ngược lại, các vectơ không phù hợp sẽ khó biến đổi hơn.

Chúng tôi viết định nghĩa của eigenvector dưới dạng một hệ phương trình:

Hãy di chuyển tất cả các thuật ngữ sang phía bên trái:

Hệ thống cuối cùng có thể được viết dưới dạng ma trận như sau:

(A - lE) X \ u003d O

Hệ kết quả luôn có nghiệm bằng không X = O. Hệ như vậy trong đó tất cả các số hạng tự do đều bằng 0 được gọi là đồng nhất. Nếu ma trận của một hệ như vậy là hình vuông, và định thức của nó không bằng 0, thì theo công thức của Cramer, chúng ta sẽ luôn nhận được một nghiệm duy nhất - không. Có thể chứng minh rằng hệ thống có các nghiệm khác 0 nếu và chỉ khi định thức của ma trận này bằng 0, tức là

| A - lE | = = 0

Phương trình với l chưa biết này được gọi là phương trình đặc trưng (Đặc biệt đa thức) ma trận A (toán tử tuyến tính).

Có thể chứng minh rằng đa thức đặc trưng của toán tử tuyến tính không phụ thuộc vào việc chọn cơ sở.

Ví dụ, hãy tìm các giá trị riêng và hiệu riêng của toán tử tuyến tính được cho bởi ma trận A =.

Để làm điều này, chúng tôi soạn phương trình đặc trưng | А - lЕ | = \ u003d (1 - l) 2 - 36 \ u003d 1 - 2l + l 2 - 36 \ u003d l 2 - 2l - 35 \ u003d 0; D \ u003d 4 + 140 \ u003d 144; giá trị riêng l 1 = (2 - 12) / 2 = -5; l 2 \ u003d (2 + 12) / 2 \ u003d 7.

Để tìm các eigenvectors, chúng ta giải hai hệ phương trình

(A + 5E) X = O

(A - 7E) X = O

Đối với cái đầu tiên trong số chúng, ma trận mở rộng sẽ có dạng

,

khi x 2 \ u003d c, x 1 + (2/3) c \ u003d 0; x 1 \ u003d - (2/3) giây, tức là X (1) \ u003d (- (2/3) s; s).

Đối với phần thứ hai, ma trận mở rộng sẽ có dạng

,

khi x 2 \ u003d c 1, x 1 - (2/3) c 1 \ u003d 0; x 1 \ u003d (2/3) s 1, tức là X (2) \ u003d ((2/3) s 1; s 1).

Do đó, các ký tự riêng của toán tử tuyến tính này là tất cả các vectơ có dạng (- (2/3) c; c) với giá trị riêng (-5) và tất cả các vectơ có dạng ((2/3) c 1; c 1) với giá trị đặc biệt 7.

Có thể chứng minh rằng ma trận của toán tử A trong cơ sở bao gồm các ký tự riêng của nó là đường chéo và có dạng:

,

trong đó tôi là các giá trị riêng của ma trận này.

Điều ngược lại cũng đúng: nếu ma trận A trong một cơ sở nào đó là đường chéo, thì tất cả các vectơ của cơ sở này sẽ là các ký tự riêng của ma trận này.

Cũng có thể chứng minh rằng nếu một toán tử tuyến tính có n giá trị riêng phân biệt theo từng cặp, thì các ký tự riêng tương ứng là độc lập tuyến tính và ma trận của toán tử này trong cơ sở tương ứng có dạng đường chéo.

Hãy giải thích điều này với ví dụ trước. Chúng ta hãy lấy các giá trị khác 0 tùy ý c và c 1, nhưng sao cho các vectơ X (1) và X (2) là độc lập tuyến tính, tức là sẽ tạo thành một cơ sở. Ví dụ: đặt c \ u003d c 1 \ u003d 3, sau đó X (1) \ u003d (-2; 3), X (2) \ u003d (2; 3).

Hãy để chúng tôi xác minh tính độc lập tuyến tính của các vectơ này:

12 ≠ 0. Trong cơ sở mới này, ma trận A sẽ có dạng A * =.

Để xác minh điều này, chúng tôi sử dụng công thức A * = C -1 AC. Trước hết chúng ta hãy tìm C -1.

C -1 = ;

Dạng bậc hai

dạng bậc hai f (x 1, x 2, xn) từ n biến được gọi là tổng, mỗi số hạng là bình phương của một trong các biến hoặc tích của hai biến khác nhau, được lấy với một hệ số nhất định: f (x 1 , x 2, xn) = (a ij = a ji).

Ma trận A, bao gồm các hệ số này, được gọi là ma trận dạng bậc hai. Nó luôn luôn đối xứng ma trận (tức là ma trận đối xứng qua đường chéo chính, a ij = a ji).

Trong ký hiệu ma trận, dạng bậc hai có dạng f (X) = X T AX, trong đó

Thực vậy

Ví dụ, chúng ta hãy viết căn thức bậc hai dưới dạng ma trận.

Để làm điều này, chúng ta tìm một ma trận có dạng bậc hai. Các phần tử đường chéo của nó bằng các hệ số tại bình phương của các biến, và các phần tử còn lại bằng một nửa các hệ số tương ứng của dạng bậc hai. Đó là lý do tại sao

Cho cột ma trận của các biến X có được bằng một phép biến đổi tuyến tính không sinh ra của cột ma trận Y, tức là X = CY, trong đó C là ma trận không suy biến bậc n. Khi đó dạng bậc hai f (X) = X T AX = (CY) T A (CY) = (Y T C T) A (CY) = Y T (C T AC) Y.

Như vậy, dưới một phép biến đổi tuyến tính không suy biến C, ma trận của bậc hai có dạng: A * = C T AC.

Ví dụ, hãy tìm dạng bậc hai f (y 1, y 2) thu được từ dạng bậc hai f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 bằng một phép biến đổi tuyến tính.

Dạng bậc hai được gọi là kinh điển(Nó có chế độ xem kinh điển) nếu tất cả các hệ số của nó a ij = 0 với i ≠ j, tức là
f (x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Ma trận của nó là đường chéo.

Định lý(bằng chứng không được đưa ra ở đây). Bất kỳ dạng bậc hai nào cũng có thể được rút gọn thành dạng chính tắc bằng cách sử dụng một phép biến đổi tuyến tính không suy biến.

Ví dụ, chúng ta hãy rút gọn về dạng chính tắc ở dạng bậc hai
f (x 1, x 2, x 3) \ u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Để thực hiện việc này, trước tiên hãy chọn hình vuông đầy đủ cho biến x 1:

f (x 1, x 2, x 3) \ u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \ u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3.

Bây giờ chúng ta chọn hình vuông đầy đủ cho biến x 2:

f (x 1, x 2, x 3) \ u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\ u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Khi đó phép biến đổi tuyến tính không suy biến y 1 \ u003d x 1 + x 2, y 2 \ u003d x 2 + (1/10) x 3 và y 3 \ u003d x 3 đưa dạng bậc hai này về dạng chính tắc f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20) y 3 2.

Lưu ý rằng dạng chính tắc của một dạng bậc hai được xác định một cách mơ hồ (cùng một dạng bậc hai có thể được rút gọn thành dạng chính tắc theo những cách khác nhau). Tuy nhiên, các dạng chính tắc thu được bằng nhiều phương pháp khác nhau có một số đặc tính chung. Đặc biệt, số hạng có hệ số dương (âm) của dạng bậc hai không phụ thuộc vào cách rút gọn dạng này về dạng này (ví dụ, trong ví dụ đang xét sẽ luôn có hai hệ số âm và một hệ số dương). Tính chất này được gọi là quy luật quán tính của dạng bậc hai.

Hãy để chúng tôi kiểm chứng điều này bằng cách rút gọn cùng một dạng bậc hai về dạng chính tắc theo một cách khác. Hãy bắt đầu phép biến đổi với biến x 2:

f (x 1, x 2, x 3) \ u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \ u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \ u003d - 3 (x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\ u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, trong đó y 1 \ u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \ u003d (2/3) x 1 + (1/6 ) x 3 và y 3 = x 1. Ở đây, hệ số âm -3 tại y 1 và hai hệ số dương 3 và 2 tại y 2 và y 3 (và sử dụng phương pháp khác, chúng tôi nhận được hệ số âm (-5) tại y 2 và hai hệ số dương: 2 tại y 1 và 1/20 cho y 3).

Cũng cần lưu ý rằng hạng của ma trận có dạng bậc hai, được gọi là bậc của dạng bậc hai, bằng số hệ số khác không của dạng chính tắc và không thay đổi trong các phép biến đổi tuyến tính.

Dạng bậc hai f (X) được gọi là tích cực (phủ định) chắc chắn, nếu với tất cả các giá trị của các biến không đồng thời bằng 0, thì nó là giá trị dương, tức là f (X)> 0 (âm, tức là
f (X)< 0).

Ví dụ, dạng bậc hai f 1 (X) \ u003d x 1 2 + x 2 2 là xác định dương, bởi vì là tổng bình phương và dạng bậc hai f 2 (X) \ u003d -x 1 2 + 2x 1 x 2 - x 2 2 là xác định âm, bởi vì biểu diễn nó có thể được biểu diễn dưới dạng f 2 (X) \ u003d - (x 1 - x 2) 2.

Trong hầu hết các tình huống thực tế, hơi khó khăn hơn để thiết lập tính xác định dấu của một dạng bậc hai, vì vậy một trong các định lý sau được sử dụng cho điều này (chúng tôi xây dựng chúng mà không cần chứng minh).

Định lý. Dạng bậc hai là dương (âm) xác định nếu và chỉ khi tất cả các giá trị riêng của ma trận của nó là dương (âm).

Định lý(Tiêu chí của Sylvester). Dạng bậc hai là xác định dương nếu và chỉ khi tất cả các phần tử chính của ma trận dạng này đều dương.

Major (góc) nhỏĐịnh thức bậc k của ma trận A bậc n được gọi là định thức của ma trận, bao gồm k hàng và cột đầu tiên của ma trận A ().

Lưu ý rằng đối với các dạng bậc hai xác định phủ định, các dấu hiệu của các dấu phụ chính thay thế và các dấu phụ bậc nhất phải là số âm.

Ví dụ, chúng ta kiểm tra dạng thức bậc hai f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 về tính xác định của dấu.

= (2 - l) *
* (3 - l) - 4 \ u003d (6 - 2l - 3l + l 2) - 4 \ u003d l 2 - 5l + 2 \ u003d 0; D = 25 - 8 = 17;
. Do đó, dạng bậc hai là xác định dương.

Phương pháp 2. Con chính bậc nhất của ma trận AD 1 = a 11 = 2> 0. Con chính bậc hai D 2 = = 6 - 4 = 2> 0. Do đó, theo tiêu chí Sylvester, dạng bậc hai là xác định dương.

Chúng ta kiểm tra một dạng bậc hai khác về tính xác định của dấu, f (x 1, x 2) \ u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Cách 1. Hãy xây dựng ma trận dạng bậc hai А =. Phương trình đặc trưng sẽ có dạng = (-2 - l) *
* (- 3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Do đó, dạng bậc hai là xác định âm.

Cách 2. Số chính phương bậc nhất của ma trận A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Do đó, theo tiêu chí Sylvester, dạng bậc hai là xác định âm (các dấu hiệu của các phụ chính thay thế nhau, bắt đầu từ trừ).

Và như một ví dụ khác, chúng ta kiểm tra dạng bậc hai f (x 1, x 2) \ u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 về tính xác định của dấu.

Cách 1. Hãy xây dựng ma trận dạng bậc hai А =. Phương trình đặc trưng sẽ có dạng = (2 - l) *
* (- 3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Một trong những số này là số âm và số còn lại là số dương. Các dấu hiệu của các giá trị riêng là khác nhau. Do đó, một dạng bậc hai không thể là xác định âm hoặc xác định dương, tức là dạng bậc hai này không xác định dấu (nó có thể nhận các giá trị của bất kỳ dấu hiệu nào).

Cách 2. Số chính phụ bậc nhất của ma trận A D 1 = a 11 = 2> 0. Số hạng chính phụ bậc hai D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).