Esimerkkejä merkittävien rajojen ratkaisemisesta. Toinen ihana raja

On olemassa useita upeita rajoja, mutta tunnetuimmat ovat ensimmäinen ja toinen ihana raja. Merkittävää näissä rajoissa on, että niitä käytetään laajalti ja niitä voidaan käyttää muiden lukuisten ongelmien löytämiseen. Tätä teemme tämän oppitunnin käytännön osassa. Ongelmien ratkaisemiseksi laskemalla ensimmäiseen tai toiseen merkittävään rajaan ei ole tarpeen paljastaa niihin sisältyviä epävarmuustekijöitä, koska suuret matemaatikot ovat jo pitkään päättäneet näiden rajojen arvot.

Ensimmäinen merkittävä raja jota kutsutaan äärettömän pienen kaaren sinin suhteen rajaksi samaan kaareen, ilmaistuna radiaanimittana:

Jatketaan ongelmien ratkaisemista ensimmäisellä merkittävällä rajalla. Huomaa: jos trigonometrinen funktio on rajamerkin alla, tämä on lähes varma merkki siitä, että tämä lauseke voidaan vähentää ensimmäiseen merkittävään rajaan.

Esimerkki 1 Löydä raja.

Ratkaisu. Korvaus sen sijaan x nolla johtaa epävarmuuteen:

Nimittäjä on sini, joten lauseke voidaan vähentää ensimmäiseen merkittävään rajaan. Aloitetaan muunnos:

Nimittäjässä - kolmen x:n sini, ja osoittajassa on vain yksi x, mikä tarkoittaa, että sinun on saatava kolme x:ää osoittajaan. Minkä vuoksi? Esitellä 3 x = a ja saada ilmaisu.

Ja tulemme ensimmäisen merkittävän rajan muunnelmaan:

koska sillä ei ole väliä mikä kirjain (muuttuja) tässä kaavassa on X:n sijaan.

Kerromme x kolmella ja jaamme heti:

Mainitun ensimmäisen merkittävän rajan mukaisesti korvaamme murtolausekkeen:

Nyt voimme vihdoin ratkaista tämän rajan:

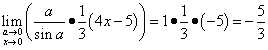Esimerkki 2 Löydä raja.

Ratkaisu. Suora korvaaminen johtaa jälleen "nolla jakaa nollalla" -epävarmuuteen:

Ensimmäisen merkittävän rajan saamiseksi on välttämätöntä, että osoittajan sinimerkin alla oleva x ja nimittäjässä oleva x ovat samalla kertoimella. Olkoon tämä kerroin yhtä suuri kuin 2. Kuvittele tätä varten nykyinen kerroin kohdassa x, kuten alla, suorittamalla toimia murtoluvuilla, saamme:

Esimerkki 3 Löydä raja.

Ratkaisu. Korvattaessa saamme jälleen epävarmuuden "nolla jaettuna nollalla":

Luultavasti ymmärrät jo, että alkuperäisestä lausekkeesta saat ensimmäisen ihanan rajan kerrottuna ensimmäisellä upealla rajalla. Tätä varten jaamme osoittajassa olevan x:n ja nimittäjän sinin neliöt samoihin tekijöihin, ja saadaksemme samat kertoimet x:lle ja sinille jaamme osoittajan x:n kolmella ja kerrotaan välittömästi kolmella. Saamme:

Esimerkki 4 Löydä raja.

Ratkaisu. Jälleen saadaan epävarmuus "nolla jaettuna nollalla":

Voimme saada kahden ensimmäisen merkittävän rajan suhteen. Jaamme sekä osoittajan että nimittäjän x:llä. Sitten, jotta kertoimet sinissä ja x:ssä ovat samat, kerrotaan ylempi x 2:lla ja jaetaan välittömästi kahdella ja kerrotaan alempi x 3:lla ja jaetaan välittömästi 3:lla.

Esimerkki 5 Löydä raja.

Ratkaisu. Ja taas "nolla jaettuna nollalla" epävarmuus:

Muistamme trigonometriasta, että tangentti on sinin ja kosinin suhde ja nollan kosini on yhtä kuin yksi. Teemme muunnoksia ja saamme:

Esimerkki 6 Löydä raja.

Ratkaisu. Rajamerkin alla oleva trigonometrinen funktio ehdottaa jälleen ajatusta ensimmäisen merkittävän rajan soveltamisesta. Esitämme sen sinin ja kosinin suhteena.

Ensimmäistä merkittävää rajaa kutsutaan seuraavaksi tasa-arvoksi:

\begin(yhtälö)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(yhtälö)

Koska arvolla $\alpha\to(0)$ meillä on $\sin\alpha\to(0)$, sanomme, että ensimmäinen merkittävä raja paljastaa muodon $\frac(0)(0)$ määrittämättömyyden. Yleisesti ottaen kaavassa (1) muuttujan $\alpha$ sijaan, sinimerkin alla ja nimittäjässä, mikä tahansa lauseke voi sijaita, kunhan kaksi ehtoa täyttyy:

Sinimerkin alla ja nimittäjässä olevat lausekkeet pyrkivät samanaikaisesti nollaan, ts. on epävarmuus muodossa $\frac(0)(0)$.
Lausekkeet sinimerkin alla ja nimittäjässä ovat samat.

Usein käytetään myös seurauksia ensimmäisestä merkittävästä rajasta:

\begin(yhtälö) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(yhtälö) \begin(yhtälö) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(yhtälö) \begin(yhtälö) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(yhtälö)

Tällä sivulla on ratkaistu yksitoista esimerkkiä. Esimerkki nro 1 on omistettu kaavojen (2)-(4) todistukselle. Esimerkit #2, #3, #4 ja #5 sisältävät ratkaisuja yksityiskohtaisine kommentteineen. Esimerkit 6-10 sisältävät ratkaisuja, joissa on vähän tai ei ollenkaan kommentteja, kuten edellisissä esimerkeissä annettiin yksityiskohtaiset selitykset. Ratkaisussa käytetään joitain trigonometrisiä kaavoja, jotka löytyvät.

Huomaan, että trigonometristen funktioiden läsnäolo yhdistettynä $\frac (0) (0)$ epävarmuuteen ei tarkoita, että ensimmäistä merkittävää rajaa on sovellettava. Joskus yksinkertaiset trigonometriset muunnokset riittävät - katso esimerkiksi.

Esimerkki #1

Todista, että $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.

a) Koska $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, niin:

$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\oikea| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$

Koska $\lim_(\alpha\to(0))\cos(0)=1$ ja $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$ , sitten:

$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$

b) Tehdään korvaus $\alpha=\sin(y)$. Koska $\sin(0)=0$, niin ehdosta $\alpha\to(0)$ meillä on $y\to(0)$. Lisäksi on nollan ympäristö, jossa $\arcsin\alpha=\arcsin(\sin(y))=y$, joten:

$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\oikea| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$

Yhtälö $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ on todistettu.

c) Tehdään korvaus $\alpha=\tg(y)$. Koska $\tg(0)=0$, ehdot $\alpha\to(0)$ ja $y\to(0)$ ovat vastaavat. Lisäksi on nollan naapurusto, jossa $\arctg\alpha=\arctg\tg(y))=y$, joten luotaen kohdan a) tuloksiin meillä on:

$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\oikea| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$

Yhtälö $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ on todistettu.

Yhtälöitä a), b), c) käytetään usein yhdessä ensimmäisen merkittävän rajan kanssa.

Esimerkki #2

Laske raja $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)( x+7))$.

Koska $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ ja $\lim_( x \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, ts. ja murtoluvun osoittaja ja nimittäjä pyrkivät samanaikaisesti nollaan, niin tässä on kyse muotoa $\frac(0)(0)$ olevasta epävarmuudesta, ts. suoritettu. Lisäksi voidaan nähdä, että lausekkeet sinimerkin alla ja nimittäjässä ovat samat (eli ja täyttyvät):

Joten molemmat sivun alussa luetellut ehdot täyttyvät. Tästä seuraa, että kaava on sovellettavissa, ts. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7) ))=1$.

Vastaus: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.

Esimerkki #3

Etsi $\lim_(x\to(0))\frac(\sin(9x))(x)$.

Koska $\lim_(x\to(0))\sin(9x)=0$ ja $\lim_(x\to(0))x=0$, kyseessä on muodon $\frac() epävarmuus 0 )(0)$, eli suoritettu. Sinimerkin alla ja nimittäjässä olevat lausekkeet eivät kuitenkaan täsmää. Tässä on tarpeen säätää nimittäjässä oleva lauseke haluttuun muotoon. Tarvitsemme lausekkeen $9x$ olevan nimittäjässä - silloin siitä tulee totta. Pohjimmiltaan meiltä puuttuu 9$-tekijä nimittäjästä, jonka syöttäminen ei ole niin vaikeaa, kerro vain nimittäjässä oleva lauseke 9$:lla. Tietenkin, jotta voit kompensoida kertolaskua $9$:lla, sinun on jaettava välittömästi 9$:lla ja jaettava:

$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x) $$

Nyt lausekkeet nimittäjässä ja sinimerkin alla ovat samat. Molemmat rajan $\lim_(x\to(0))\frac(\sin(9x))(9x)$ ehdot täyttyvät. Tästä syystä $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. Ja tämä tarkoittaa, että:

9 $\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$

Vastaus: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.

Esimerkki #4

Etsi $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.

Koska $\lim_(x\to(0))\sin(5x)=0$ ja $\lim_(x\to(0))\tg(8x)=0$, tässä on kyse muodossa $\frac(0)(0)$. Ensimmäisen merkittävän rajan muoto on kuitenkin rikki. Osoittaja, joka sisältää $\sin(5x)$, vaatii $5x$ nimittäjän. Tässä tilanteessa helpoin tapa on jakaa osoittaja $5x$:lla ja kertoa heti $5x$:lla. Lisäksi suoritamme samanlaisen toimenpiteen nimittäjällä kertomalla ja jakamalla $\tg(8x)$ $8x$:lla:

$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$

Pienentämällä $x$ ja ottamalla vakio $\frac(5)(8)$ pois rajamerkistä, saamme:

$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$

Huomaa, että $\lim_(x\to(0))\frac(\sin(5x))(5x)$ täyttää täysin ensimmäisen merkittävän rajan vaatimukset. Löytääksesi $\lim_(x\to(0))\frac(\tg(8x))(8x)$ käytetään seuraavaa kaavaa:

$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$

Vastaus: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.

Esimerkki #5

Etsi $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.

Koska $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (muista, että $\cos(0)=1$) ja $\ lim_(x\to(0))x^2=0$, niin kyseessä on muodon $\frac(0)(0)$ määrittelemättömyys. Ensimmäisen ihanan rajan soveltamiseksi sinun tulee kuitenkin päästä eroon osoittajassa olevasta kosinista siirtymällä sineihin (kaavan soveltamiseksi) tai tangenteihin (kaavan soveltamiseksi). Voit tehdä tämän seuraavalla muunnolla:

$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\oikea)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\oikea)=\cos(5x)\cdot\sin^2(5x).$$

Palataan rajaan:

$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\oikea| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\oikea) $$

Murtoluku $\frac(\sin^2(5x))(x^2)$ on jo lähellä muotoa, joka vaaditaan ensimmäiselle merkittävälle rajalle. Työstetään vähän murto-osan $\frac(\sin^2(5x))(x^2)$ kanssa ja sovitetaan se ensimmäiseen upeaan rajaan (huomaa, että osoittajan ja sinin alla olevien lausekkeiden on vastattava):

$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$

Palataan harkittuun rajaan:

$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\oikea) =\lim_(x\to(0) ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$

Vastaus: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.

Esimerkki #6

Etsi raja $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.

Koska $\lim_(x\to(0))(1-\cos(6x))=0$ ja $\lim_(x\to(0))(1-\cos(2x))=0$, niin käsittelemme epävarmuutta $\frac(0)(0)$. Avataan se ensimmäisen merkittävän rajan avulla. Tätä varten siirrytään kosinuksista sineihin. Koska $1-\cos(2\alpha)=2\sin^2(\alpha)$, niin:

$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$

Kun ohitetaan annettu raja sineille, meillä on:

$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\) frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\oikea)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x) \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$

Vastaus: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.

Esimerkki #7

Laske raja $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ annettu $\alpha\neq\ beta $.

Yksityiskohtaiset selitykset annettiin aiemmin, mutta tässä on vain huomautettava, että $\frac(0)(0)$ on jälleen määrittelemätön. Siirrytään kosineista sineihin kaavan avulla

$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$

Yllä olevaa kaavaa käyttämällä saamme:

$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\oikea| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta) )(2)\oikea)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac) (\alpha-\beta)(2)\oikea))(x)\oikea)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x) \cdot\frac(\alpha+\beta)(2)\oikea))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alfa^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2). $$

Vastaus: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alfa^2)(2)$.

Esimerkki #8

Etsi raja $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.

Koska $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (muista, että $\sin(0)=\tg(0)=0$) ja $\ lim_(x\to(0))x^3=0$, niin tässä on kyse muodon $\frac(0)(0)$ määrittämättömyydestä. Puretaan se näin:

$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\oikea| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\oikea))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\oikea))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\oikea)^2\cdot\frac(1)(\cos(x))\oikea) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1) ) =\frac(1)(2). $$

Vastaus: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.

Esimerkki #9

Etsi raja $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.

Koska $\lim_(x\to(3))(1-\cos(x-3))=0$ ja $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$, silloin on määrittämättömyys muodossa $\frac(0)(0)$. Ennen kuin jatkat sen laajentamista, on kätevää muuttaa muuttuja siten, että uusi muuttuja pyrkii nollaan (huomaa, että muuttuja $\alpha \to 0$ kaavoissa). Helpoin tapa on ottaa käyttöön muuttuja $t=x-3$. Kuitenkin jatkomuunnosten helpottamiseksi (tämä etu näkyy alla olevan ratkaisun aikana) kannattaa tehdä seuraava korvaus: $t=\frac(x-3)(2)$. Huomautan, että molemmat korvaukset ovat sovellettavissa tässä tapauksessa, vain toinen vaihto antaa sinun työskennellä vähemmän murtolukujen kanssa. Alkaen $x\to(3)$, sitten $t\to(0)$.

$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\oikea| =\left|\begin(tasattu)&t=\frac(x-3)(2);\\&t\to(0)\end(tasattu)\oikea| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\oikea) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$

Vastaus: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.

Esimerkki #10

Etsi raja $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^ 2) $.

Jälleen olemme tekemisissä $\frac(0)(0)$ epävarmuuden kanssa. Ennen kuin jatkat sen laajentamista, on kätevää muuttaa muuttuja siten, että uusi muuttuja pyrkii nollaan (huomaa, että muuttuja on kaavoissa $\alpha\to(0)$). Helpoin tapa on ottaa käyttöön muuttuja $t=\frac(\pi)(2)-x$. Alkaen $x\to\frac(\pi)(2)$, sitten $t\to(0)$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\left|\frac(0)(0)\oikea| =\left|\begin(tasattu)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(tasattu)\oikea| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\oikea))(t^2) =\lim_(t\to(0) ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$

Vastaus: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.

Esimerkki #11

Etsi rajat $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2\) pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.

Tässä tapauksessa meidän ei tarvitse käyttää ensimmäistä ihanaa rajaa. Huomaa: sekä ensimmäisessä että toisessa rajassa on vain trigonometrisiä funktioita ja numeroita. Usein tällaisissa esimerkeissä on mahdollista yksinkertaistaa rajamerkin alla olevaa lauseketta. Lisäksi mainitun yksinkertaistamisen ja joidenkin tekijöiden vähentämisen jälkeen epävarmuus katoaa. Annoin tämän esimerkin vain yhdellä tarkoituksella: osoittaa, että trigonometristen funktioiden läsnäolo rajamerkin alla ei välttämättä tarkoita ensimmäisen merkittävän rajan soveltamista.

Koska $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (muista, että $\sin\frac(\pi)(2)=1$) ja $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (muista, että $\cos\frac(\pi)(2)=0$), silloin on kyse epävarmuudesta muodossa $\frac(0)(0)$. Tämä ei kuitenkaan tarkoita ollenkaan, että meidän pitäisi käyttää ensimmäistä merkittävää rajaa. Epävarmuuden paljastamiseksi riittää, kun huomioidaan, että $\cos^2x=1-\sin^2x$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\oikea| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$

Vastaava ratkaisu on Demidovichin ratkaisukirjassa (nro 475). Toisen rajan osalta, kuten tämän osan edellisissä esimerkeissä, meillä on epävarmuus muodossa $\frac(0)(0)$. Miksi se syntyy? Se syntyy, koska $\tg\frac(2\pi)(3)=-\sqrt(3)$ ja $2\cos\frac(2\pi)(3)=-1$. Käytämme näitä arvoja muuttamaan lausekkeita osoittajassa ja nimittäjässä. Toimintamme tarkoitus: kirjoita summa osoittajaan ja nimittäjään tulona. Muuten, usein on kätevää muuttaa muuttuja samanlaisen muodon sisällä niin, että uusi muuttuja pyrkii nollaan (katso esimerkiksi tällä sivulla olevat esimerkit nro 9 tai nro 10). Tässä esimerkissä ei kuitenkaan ole mitään järkeä vaihtaa muuttujaa, vaikka haluttaessa muuttujan $t=x-\frac(2\pi)(3)$ korvaaminen on helppo toteuttaa.

$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\oikea )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\oikea))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin) \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac) (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\oikea)) =-\frac(4 )(\sqrt(3)). $$

Kuten näet, meidän ei tarvinnut soveltaa ensimmäistä upeaa rajaa. Tietenkin tämä voidaan tehdä haluttaessa (katso huomautus alla), mutta se ei ole välttämätöntä.

Mikä olisi ratkaisu käyttämällä ensimmäistä merkittävää rajaa? näytä piilota

Käyttämällä ensimmäistä merkittävää rajaa saamme:

$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi) )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ oikea))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\oikea)) =-\frac(4)(\sqrt( 3)). $$

Vastaus: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.

Löydä upeita rajoja se on vaikeaa paitsi monille ensimmäisen, toisen vuoden opiskelijoille, jotka opiskelevat rajojen teoriaa, vaan myös joillekin opettajille.

Ensimmäisen merkittävän rajan kaava

Ensimmäisen merkittävän rajan seuraukset kirjoittaa kaavat
1. 2. 3. 4. Mutta sinänsä merkittävien rajojen yleiset kaavat eivät auta ketään kokeessa tai kokeessa. Lopputulos on, että todelliset tehtävät rakennetaan niin, että yllä kirjoitettuihin kaavoihin on vielä päästävä. Ja suurin osa opiskelijoista, jotka jättävät tunteja väliin, opiskelevat tätä kurssia kirjeitse tai joiden opettajat eivät aina ymmärrä, mistä he selittävät, eivät osaa laskea alkeellisia esimerkkejä merkittäviin rajoihin. Ensimmäisen merkittävän rajan kaavoista näemme, että niillä voidaan tutkia epävarmuuksia, kuten nolla jaettuna nollalla lausekkeissa, joissa on trigonometrisiä funktioita. Tarkastellaan ensin sarjaa esimerkkejä ensimmäisestä merkittävästä rajasta ja sitten tutkitaan toista merkittävää rajaa.

Esimerkki 1. Etsi funktion sin(7*x)/(5*x) raja
Ratkaisu: Kuten näette, rajan alla oleva funktio on lähellä ensimmäistä merkittävää rajaa, mutta itse funktion raja ei todellakaan ole yhtä suuri. Tällaisissa rajojen määrittämisessä nimittäjästä tulee erottaa muuttuja, jolla on sama kerroin kuin sinin alla oleva muuttuja. Tässä tapauksessa jaa ja kerro 7:llä

Joillekin sellaiset yksityiskohdat näyttävät tarpeettomilta, mutta useimmille opiskelijoille, joiden on vaikea antaa rajoja, se auttaa ymmärtämään paremmin sääntöjä ja oppimaan teoreettista materiaalia.
Lisäksi, jos funktiolla on käänteinen muoto - tämä on myös ensimmäinen upea raja. Ja kaikki, koska ihana raja on yhtä suuri kuin yksi

Sama sääntö koskee 1 merkittävän rajan seurauksia. Siksi, jos sinulta kysytään "Mikä on ensimmäinen ihmeellinen raja?" Sinun on vastattava epäröimättä, että se on yksikkö.

Esimerkki 2. Etsi funktion sin(6x)/tan(11x) raja
Ratkaisu: Ymmärtääksemme lopputuloksen, kirjoitamme funktion muotoon

Merkittävän rajan sääntöjen soveltamiseksi kerrotaan ja jaetaan kertoimilla

Seuraavaksi kirjoitetaan funktioiden tulon raja rajojen tulona

Ilman monimutkaisia kaavoja löysimme muutaman trigonometrisen funktion rajan. Hallitaksesi yksinkertaisia kaavoja, yritä keksiä ja löytää raja 2:lle ja 4:lle, kaavan 1 seuraus upeasta rajasta. Harkitsemme monimutkaisempia tehtäviä.

Esimerkki 3. Laske raja (1-cos(x))/x^2
Ratkaisu: Kun tarkistetaan korvauksella, saamme epävarmuuden 0/0 . Monet eivät tiedä kuinka pienentää tällaista esimerkkiä yhteen upeaan rajaan. Tässä sinun tulee käyttää trigonometristä kaavaa

Tässä tapauksessa raja muutetaan selkeään muotoon

Olemme onnistuneet pienentämään funktion merkittävän rajan neliöön.

Esimerkki 4. Etsi raja
Ratkaisu: Korvattaessa saamme tutun ominaisuuden 0/0 . Muuttuja kuitenkin lähestyy Pi:tä, ei nollaa. Siksi, jotta voidaan soveltaa ensimmäistä merkittävää rajaa, muutetaan muuttujaa x siten, että uusi muuttuja menee nollaan. Tätä varten merkitsemme nimittäjäksi uudeksi muuttujaksi Pi-x=y

Siten käyttämällä trigonometristä kaavaa, joka on annettu edellisessä tehtävässä, esimerkki pienennetään 1 upeaan rajaan.

Esimerkki 5 Laske raja
Ratkaisu: Aluksi ei ole selvää, kuinka rajoja yksinkertaistaa. Mutta jos on esimerkki, siihen on oltava vastaus. Se, että muuttuja menee yksikköön, antaa korvattaessa singulaarisuuden muodossa nolla kerrottuna äärettömyydellä, joten tangentti on korvattava kaavalla

Sen jälkeen saadaan haluttu epävarmuus 0/0. Seuraavaksi teemme muuttujien muutoksen rajassa ja käytämme kotangentin jaksollisuutta

Viimeiset korvaukset antavat meille mahdollisuuden käyttää merkittävän rajan seurausta 1.

Toinen merkittävä raja on yhtä suuri kuin eksponentti

Tämä on klassikko, jonka rajoja todellisissa ongelmissa ei aina ole helppo saavuttaa.
Laskelmia varten tarvitset rajat ovat seurauksia toisesta merkittävästä rajasta:
1. 2. 3. 4.
Toisen merkittävän rajan ja sen seurausten ansiosta voidaan tutkia epävarmuustekijöitä, kuten nolla jaettuna nollalla, yksi äärettömän potenssiin ja ääretön jaettuna äärettömyydellä ja jopa samassa määrin.

Aloitetaan muutamilla yksinkertaisilla esimerkeillä.

Esimerkki 6 Etsi funktion raja
Ratkaisu: Käytä suoraan 2 ihanaa rajaa ei toimi. Ensin sinun on käännettävä ilmaisin siten, että sen muoto on käänteinen suluissa olevalle termille

Tämä on tekniikka, jolla vähennetään 2 merkittävään rajaan ja itse asiassa rajan seurauksen kaavan 2 johtaminen.

Esimerkki 7 Etsi funktion raja
Ratkaisu: Meillä on tehtävät merkittävän rajan seurauksen 2 kaavalle 3. Nollasubstituutio antaa singulaarisuuden muodossa 0/0. Nostaaksesi säännön alaista rajaa, käännämme nimittäjää niin, että muuttujalla on sama kerroin kuin logaritmissa

Se on myös helppo ymmärtää ja suorittaa kokeessa. Opiskelijoiden vaikeudet rajojen laskemisessa alkavat seuraavista tehtävistä.

Esimerkki 8 Laske funktioraja[(x+7)/(x-3)]^(x-2)
Ratkaisu: Meillä on tyypin 1 singulariteetti äärettömyyden potenssiin. Jos et usko minua, voit korvata äärettömän "x":n sijasta kaikkialla ja nähdä itse. Nostaaksesi säännön mukaisesti jaamme osoittajan suluissa olevalla nimittäjällä, tätä varten suoritamme ensin manipulaatiot

Korvaa lauseke rajaksi ja käännä se 2 ihanaksi rajaksi

Raja on 10:n potenssin eksponentti. Vakiot, jotka ovat termejä, joissa on muuttuja sekä suluissa että asteessa, eivät vaikuta "sää" - tämä tulee muistaa. Ja jos opettajat kysyvät sinulta - "Miksi et käännä ilmaisinta?" (Tälle esimerkille x-3 ), sano sitten, että "Kun muuttuja pyrkii äärettömään, lisää siihen 100 tai vähennä 1000, niin raja pysyy samana!".
On olemassa toinen tapa laskea tämän tyyppiset rajat. Puhumme siitä seuraavassa tehtävässä.

Esimerkki 9 Löydä raja
Ratkaisu: Nyt poistamme muuttujan osoittajasta ja nimittäjästä ja muutamme yhden ominaisuuden toiseksi. Lopullisen arvon saamiseksi käytämme merkittävän rajan seurauksen 2 kaavaa

Esimerkki 10 Etsi funktion raja
Ratkaisu: Kaikki eivät löydä annettua rajaa. Nostaaksesi rajan 2:een kuvittele, että sin (3x) on muuttuja ja sinun on käännettävä eksponenttia

Seuraavaksi kirjoitetaan indikaattori asteeksi asteessa

Väliargumentit on kuvattu suluissa. Ensimmäisen ja toisen upean rajan käytön seurauksena saimme kuutioisen eksponentin.

Esimerkki 11. Laske funktioraja sin(2*x)/log(3*x+1)
Ratkaisu: Meillä on epävarmuus muotoa 0/0. Lisäksi näemme, että funktio tulisi muuntaa käyttämään molempia upeita rajoja. Suoritetaan edelliset matemaattiset muunnokset

Lisäksi ilman vaikeuksia raja ottaa arvon

Näin tunnet olosi kotoisaksi testeissä, testeissä, moduuleissa, jos opit maalaamaan toimintoja nopeasti ja pienentämään ne ensimmäiseen tai toiseen upeaan rajaan. Jos sinun on vaikea muistaa yllä olevia tapoja löytää rajoja, voit aina tilata meiltä rajojen tarkastustyön.
Voit tehdä tämän täyttämällä lomakkeen, määrittämällä tiedot ja liittämällä tiedostoon esimerkkejä. Olemme auttaneet monia opiskelijoita - voimme auttaa myös sinua!

Nyt rauhallisin mielin siirrymme harkintaan upeita rajoja.
näyttää .

Muuttujan x sijasta voi esiintyä erilaisia toimintoja, pääasia, että niillä on taipumus olla 0.

Meidän on laskettava raja

Kuten näette, tämä raja on hyvin samanlainen kuin ensimmäinen merkittävä, mutta tämä ei ole täysin totta. Yleensä, jos huomaat synnin rajassa, sinun tulee heti miettiä, onko mahdollista käyttää ensimmäistä merkittävää rajaa.

Sääntömme nro 1 mukaan korvaamme x:n nollalla:

Saamme epävarmuuden.

Yritetään nyt järjestää itsenäisesti ensimmäinen merkittävä raja. Tätä varten teemme yksinkertaisen yhdistelmän:

Joten järjestämme osoittajan ja nimittäjän niin, että 7x erottuu. Tuttu merkittävä raja on jo ilmestynyt. On suositeltavaa korostaa sitä päätettäessä:

Korvaamme ensimmäisen merkittävän esimerkin ratkaisun ja saamme:

Yksinkertaista murtoluku:

Vastaus: 7/3.

Kuten näet, kaikki on hyvin yksinkertaista.

On muoto , jossa e = 2,718281828… on irrationaalinen luku.

Muuttujan x sijasta voi esiintyä erilaisia toimintoja, pääasia, että ne pyrkivät .

Meidän on laskettava raja

Tässä nähdään rajamerkin alla asteen läsnäolo, mikä tarkoittaa, että toista merkittävää rajaa voidaan soveltaa.

Kuten aina, käytämme sääntöä numero 1 - korvike x:n sijaan:

Voidaan nähdä, että x:n asteen kanta on , ja eksponentti on 4x > ts. saamme muodon epävarmuuden:

Käyttäkäämme toista ihmeellistä rajaa paljastamaan epävarmuutemme, mutta ensin meidän on järjestettävä se. Kuten näet, on välttämätöntä saavuttaa läsnäolo indikaattorissa, jonka pohjaa nostetaan 3x potenssiin ja samalla 1/3x tehoon, jotta lauseke ei muutu:

Älä unohda korostaa upeaa rajaamme:

Nämä ovat todella upeita rajoja!
Jos sinulla on kysyttävää aiheesta ensimmäinen ja toinen upea raja kysy heiltä kommenteissa.
Vastaamme kaikille mahdollisimman pian.

Voit myös työskennellä opettajan kanssa tästä aiheesta.
Meillä on ilo tarjota sinulle palveluita pätevän tutorin valitsemisesta kaupungistasi. Yhteistyökumppanimme valitsevat sinulle välittömästi hyvän opettajan sinulle edullisin ehdoin.

Ei tarpeeksi tietoa? - Sinä pystyt !

Voit kirjoittaa matemaattisia laskelmia muistilehtiin. On paljon miellyttävämpää kirjoittaa yksittäisiin muistikirjoihin, joissa on logo (http://www.blocnot.ru).