Plott imaginære bilder. Bygge bilder som en tynn linse gir. Tynn linseformel

Punktbilde S i linsen vil det være et skjæringspunkt for alle refrakterte stråler eller deres fortsettelser. I det første tilfellet er bildet ekte, i det andre - imaginært. Som alltid, for å finne skjæringspunktet for alle stråler, er det nok å konstruere to. Vi kan gjøre dette ved å bruke den andre brytningsloven. For å gjøre dette må du måle innfallsvinkelen til en vilkårlig stråle, beregne brytningsvinkelen, konstruere en bruddstråle, som i en eller annen vinkel vil falle på den andre siden av linsen. Etter å ha målt denne innfallsvinkelen, er det nødvendig å beregne den nye brytningsvinkelen og konstruere den utgående strålen. Som du kan se, er arbeidet ganske arbeidskrevende, så det unngås vanligvis. I henhold til de kjente egenskapene til linsene kan tre stråler konstrueres uten noen beregninger. En stråle som faller inn parallelt med en hvilken som helst optisk akse, etter dobbel brytning, vil passere gjennom det virkelige fokuset eller fortsettelsen vil passere gjennom det imaginære fokuset. I henhold til loven om reversibilitet vil en stråle som faller inn i retning av det tilsvarende fokuset, etter dobbel refraksjon, gå ut parallelt med en viss optisk akse. Til slutt vil strålen passere gjennom det optiske sentrum av linsen uten å avvike.

På fig. 7 plottet bildepunkt S i en konvergerende linse, i fig. 8 - i spredning. Med slike konstruksjoner er den optiske hovedaksen avbildet og brennviddene F vises på den (avstander fra hovedfokusene eller fra brennplanene til objektivets optiske senter) og doble brennvidder (for konvergerende linser). Deretter ser de etter skjæringspunktet for de brutte strålene (eller deres fortsettelser), ved å bruke to av de ovennevnte.

Vanligvis er det vanskelig å konstruere et bilde av et punkt plassert på den optiske hovedaksen. For en slik konstruksjon må du ta en hvilken som helst stråle som vil være parallell med en optisk sideakse (stiplet linje i fig. 9). Etter dobbel refraksjon vil den passere gjennom et sekundærfokus, som ligger i skjæringspunktet mellom denne sekundære aksen og brennplanet. Som den andre strålen er det praktisk å bruke en stråle som går uten brytning langs den optiske hovedaksen.

På fig. 10 viser to konvergerende linser. Den andre "bedre" samler strålene, bringer dem nærmere, den er "sterkere". optisk kraft linsen kalles den gjensidige av brennvidden:

Kraften til en linse uttrykkes i dioptrier (D).

Ris. ti

En dioptri er den optiske kraften til en slik linse, hvis brennvidde er 1 m.

Konvergerende linser har en positiv brytningsstyrke, mens divergerende linser har en negativ brytningsstyrke.

Konstruksjonen av et bilde av et objekt i en konvergerende linse er redusert til konstruksjonen av dens ekstreme punkter. Velg en pil som et objekt AB(Fig. 11). Pek bilde EN konstruert som i fig. 7, prikk B1 kan bli funnet, som i fig. 19. La oss introdusere en notasjon (lik de som ble introdusert når vi vurderer speil): avstanden fra objektet til linsen | BO| = d; avstand fra objekt til bildelinse | BO 1 | = f, brennvidde | AV| = F. Fra likheten til trekanter EN 1 B 1 O og ABO (langs like skarpe - vertikale - vinkler rette trekanter lignende). Fra likheten til trekanter EN 1 B 1 F og DOF(med samme tegn på likhet) . Følgelig

Eller fF = df − dF .

Dele ligningsleddet for ledd med dFf og flytter det negative leddet til den andre siden av ligningen, får vi:

Vi har utledet linseformelen som ligner på speilformelen.

I tilfellet med en divergerende linse (fig. 22), "fungerer" det nesten imaginære fokuset. Merk at punktet A1 er skjæringspunktet for fortsettelsen av de brutte strålene, og ikke skjæringspunktet for den refrakterte strålen FD og den innfallende strålen AO.

For bevis, vurder en strålehendelse fra punkt A mot det fjerne fokuset. Etter dobbel refraksjon vil den gå ut av linsen parallelt med den optiske hovedaksen, slik at dens fortsettelse vil passere gjennom punktet A1. Bildet av punkt B kan konstrueres på samme måte som fig. 9. Fra likheten til de tilsvarende trekantene; ; fF = dF − df eller

Det er mulig å gjennomføre en studie av formelen til en linse, lik studien av formelen til et speil.

Hvordan vil bildet av et objekt endres hvis halvparten av linsen er ødelagt? Bildet vil bli mindre intenst, men verken form eller plassering vil endre seg. Tilsvarende bildet av et objekt i en hvilken som helst del av en linse eller et speil.

For å konstruere et bilde av et punkt i et ideelt system, er det tilstrekkelig å konstruere hvilke som helst to stråler som kommer fra dette punktet. Skjæringspunktet for de utgående strålene som tilsvarer disse to innfallende strålene vil være det ønskede bildet av dette punktet.

Emner for USE-kodifikatoren: bygge bilder i linser, formel tynn linse.

Reglene for strålebanen i tynne linser, formulert i , leder oss til det viktigste utsagnet.

Bildeteorem. Hvis det er et lysende punkt foran linsen, etter brytning i linsen, krysser alle stråler (eller deres fortsettelser) på ett punkt.

Punktet kalles punktbildet.

Hvis de brutte strålene selv krysser hverandre i et punkt, kalles bildet gyldig. Det kan oppnås på skjermen, siden energien til lysstrålene er konsentrert på et punkt.

Hvis imidlertid ikke de brutte strålene i seg selv krysser hverandre i et punkt, men fortsettelsen deres (dette skjer når de brutte strålene divergerer etter linsen), kalles bildet imaginært. Den kan ikke mottas på skjermen, fordi ingen energi er konsentrert i punktet. Et imaginært bilde, husker vi, oppstår på grunn av det særegne ved hjernen vår - for å fullføre de divergerende strålene til deres imaginære skjæringspunkt og se et lysende punkt i dette skjæringspunktet. Et imaginært bilde eksisterer bare i våre sinn.

Bildeteoremet fungerer som grunnlag for avbildning i tynne linser. Vi vil bevise dette teoremet for både konvergerende og divergerende linser.

Konvergerende linse: faktiske bildet poeng.

La oss først se på en konvergerende linse. La være avstanden fra punktet til objektivet, være brennvidden til objektivet. Det er to grunnleggende forskjellige saker: og (samt det mellomliggende tilfellet ). Vi vil behandle disse sakene én etter én; i hver av dem vi
La oss diskutere egenskapene til bilder av en punktkilde og et utvidet objekt.

Første tilfelle: . Punktlyskilden er plassert lenger fra linsen enn venstre brennplan (fig. 1).

Strålen som passerer gjennom det optiske senteret brytes ikke. Vi vil ta vilkårlig stråle, vi konstruerer et punkt der den refrakterte strålen skjærer med strålen, og så viser vi at posisjonen til punktet ikke avhenger av valget av strålen (med andre ord, punktet er det samme for alle mulige stråler) . Dermed viser det seg at alle stråler som kommer fra punktet skjærer hverandre i punktet etter brytning i linsen, og bildeteoremet vil bli bevist for det aktuelle tilfellet.

Vi finner poenget ved å konstruere videre trekk stråle . Vi kan gjøre dette: vi tegner en optisk sideakse parallelt med strålen til den skjærer brennplanet i sidefokuset, hvoretter vi tegner den refrakterte strålen til den skjærer med strålen i punktet.

Nå skal vi se etter avstanden fra punktet til linsen. Vi vil vise at denne avstanden kun uttrykkes i form av og , det vil si at den kun bestemmes av posisjonen til kilden og egenskapene til linsen, og er dermed ikke avhengig av en bestemt stråle.

La oss slippe perpendikulærene og inn på den optiske hovedaksen. La oss også tegne den parallelt med den optiske hovedaksen, det vil si vinkelrett på linsen. Vi får tre par like trekanter:

, (1)
, (2)
. (3)

Som et resultat har vi følgende kjede av likheter (tallet på formelen over likhetstegnet indikerer fra hvilket par like trekanter denne likheten ble oppnådd).

(4)

Men så relasjon (4) skrives om som:

. (5)

Herfra finner vi ønsket avstand fra punktet til linsen:

. (6)

Som vi ser, avhenger det egentlig ikke av valget av strålen. Derfor vil enhver stråle etter brytning i linsen passere gjennom punktet konstruert av oss, og dette punktet vil være et ekte bilde av kilden

Bildesetningen er bevist i dette tilfellet.

Den praktiske betydningen av bildeteoremet er dette. Siden alle strålene fra kilden skjærer hverandre etter linsen på ett punkt - bildet - så er det nok å ta de to mest praktiske strålene for å bygge et bilde. Akkurat hva?

Hvis kilden ikke ligger på den optiske hovedaksen, er følgende egnet som praktiske stråler:

Strålen som passerer gjennom det optiske sentrum av linsen - den brytes ikke;
- en stråle parallelt med den optiske hovedaksen - etter brytning går den gjennom fokuset.

Konstruksjonen av et bilde ved hjelp av disse strålene er vist i fig. 2.

Hvis punktet ligger på den optiske hovedaksen, gjenstår bare en praktisk stråle - som løper langs den optiske hovedaksen. Som den andre bjelken må man ta den "ubehagelige" (fig. 3).

La oss se igjen på uttrykket ( 5 ). Den kan skrives i en litt annen form, mer attraktiv og minneverdig. La oss først flytte enheten til venstre:

Vi deler nå begge sider av denne likheten med en:

(7)

Relasjon (7) kalles tynn linseformel(eller bare linseformelen). Så langt har linseformelen blitt oppnådd for tilfellet med en konvergerende linse og for . I det følgende utleder vi modifikasjoner av denne formelen for andre tilfeller.

La oss nå gå tilbake til relasjon (6) . Dens betydning er ikke begrenset til det faktum at den beviser bildeteoremet. Vi ser også at det ikke er avhengig av avstanden (fig. 1, 2) mellom kilden og den optiske hovedaksen!

Dette betyr at uansett hvilket punkt av segmentet vi tar, vil bildet være i samme avstand fra linsen. Den vil ligge på et segment - nemlig i skjæringspunktet mellom segmentet med en stråle som vil gå gjennom linsen uten brytning. Spesielt vil bildet av et punkt være et punkt .

Dermed har vi etablert et viktig faktum: segmentet er sølepytter med bildet av segmentet. Fra nå av kaller vi det originale segmentet, bildet som vi er interessert i Emne og er merket med rød pil i figurene. Vi trenger pilens retning for å følge om bildet er rett eller omvendt.

Konvergerende linse: det faktiske bildet av et objekt.

La oss gå videre til vurderingen av bilder av objekter. Husk det mens vi er innenfor rammen av saken. Her kan man skille mellom tre typiske situasjoner.

en. . Bildet av objektet er ekte, omvendt, forstørret (fig. 4; dobbeltfokus er indikert). Fra linseformelen følger det at det i dette tilfellet vil være det (hvorfor?).

En slik situasjon realiseres for eksempel i overheadprojektorer og filmkameraer - disse optiske enhetene gir et forstørret bilde av det som er på filmen på skjermen. Hvis du noen gang har vist lysbilder, så vet du at lysbildet må settes inn i projektoren opp ned – slik at bildet på skjermen ser riktig ut, og ikke snur seg opp ned.

Forholdet mellom størrelsen på bildet og størrelsen på objektet kalles den lineære forstørrelsen av linsen og er betegnet med Г - (dette er den store greske "gamma"):

Fra likheten mellom trekanter får vi:

. (8)

Formel (8) brukes i mange problemer der den lineære forstørrelsen av linsen er involvert.

2. . I dette tilfellet, fra formel (6) finner vi at og . Den lineære forstørrelsen av linsen i henhold til (8) er lik én, dvs. størrelsen på bildet er lik størrelsen på objektet (fig. 5).

Ris. 5.a=2f: bildestørrelsen er lik objektstørrelsen

3. . I dette tilfellet følger det av linseformelen at (hvorfor?). Linsens lineære forstørrelse vil være mindre enn én - bildet er ekte, invertert, redusert (fig. 6).

Denne situasjonen er vanlig for mange optiske enheter: kameraer, kikkerter, teleskoper - i et ord, de der bilder av fjerne objekter er oppnådd. Når objektet beveger seg bort fra linsen, reduseres bildet i størrelse og nærmer seg fokalplanet.

Vi har fullført behandlingen av den første saken. La oss gå videre til den andre saken. Den blir ikke like stor lenger.

Konvergerende linse: virtuelt bilde av et punkt.

Andre tilfelle: . En punktlyskilde er plassert mellom linsen og brennplanet (fig. 7).

Sammen med at strålen går uten brytning, betrakter vi igjen en vilkårlig stråle. Men nå to divergerende stråler og oppnås ved utgangen fra linsen. Vårt øye vil fortsette disse strålene til de krysser hverandre på et punkt.

Bildeteoremet sier at punktet vil være det samme for alle stråler som kommer fra punktet. Vi beviser dette igjen med tre par like trekanter:

Ved å betegne igjen gjennom avstanden fra til linsen, har vi den tilsvarende kjeden av likheter (du kan lett finne ut det allerede):

. (9)

. (10)

Verdien avhenger ikke av strålen, som beviser bildeteoremet for vårt tilfelle. Så er et virtuelt bilde av kilden. Hvis punktet ikke ligger på den optiske hovedaksen, så for å konstruere et bilde, er det mest hensiktsmessig å ta en stråle som går gjennom det optiske senteret og en stråle parallelt med den optiske hovedaksen (fig. 8).

Vel, hvis punktet ligger på den optiske hovedaksen, så er det ingen steder å gå - du må nøye deg med en stråle som faller på skrå på linsen (fig. 9).

Relasjon (9) fører oss til en variant av linseformelen for det betraktede tilfellet . Først omskriver vi denne relasjonen som:

og del deretter begge sider av den resulterende likheten med en:

. (11)

Ved å sammenligne (7) og (11) ser vi en liten forskjell: begrepet innledes med et plusstegn hvis bildet er ekte, og et minustegn hvis bildet er imaginært.

Verdien beregnet ved formel (10) avhenger heller ikke av avstanden mellom punktet og den optiske hovedaksen. Som ovenfor (husk resonnementet med en prikk), betyr dette at bildet av segmentet i fig. 9 vil være et segment.

Konvergerende linse: et virtuelt bilde av et objekt.

Med dette i tankene kan vi enkelt bygge et bilde av et objekt som befinner seg mellom linsen og brennplanet (fig. 10). Det viser seg å være imaginært, direkte og forstørret.

Du ser et slikt bilde når du ser på en liten gjenstand i et forstørrelsesglass – et forstørrelsesglass. Kassen er fullstendig demontert. Som du kan se, er det kvalitativt forskjellig fra vårt første tilfelle. Dette er ikke overraskende - mellom dem ligger en mellomliggende "katastrofal" sak.

Konvergerende linse: Et objekt i fokalplanet.

Mellomsak: Lyskilden er plassert i fokalplanet til linsen (fig. 11).

Som vi husker fra forrige avsnitt, vil strålene til en parallell stråle, etter brytning i en konvergerende linse, skjære seg i fokalplanet - nemlig ved hovedfokuset hvis strålen faller inn vinkelrett på linsen, og ved sidefokuset hvis strålen faller inn på skrå. Ved å bruke reversibiliteten til banen til strålene, konkluderer vi med at alle strålene til kilden som ligger i fokalplanet, etter å ha forlatt linsen, vil gå parallelt med hverandre.

Ris. 11. a=f: ingen bilde

Hvor er bildet av prikken? Det er ingen bilder. Imidlertid er det ingen som forbyr oss å anta at parallelle stråler krysser hverandre på et uendelig fjernt punkt. Da forblir bildeteoremet gyldig i dette tilfellet, bildet er på uendelig.

Følgelig, hvis objektet er helt plassert i fokalplanet, vil bildet av dette objektet bli lokalisert i det uendelige(eller, det som er det samme, vil være fraværende).

Så vi har fullstendig vurdert konstruksjonen av bilder i en konvergerende linse.

Konvergerende linse: virtuelt bilde av et punkt.

Heldigvis er det ikke så mange situasjoner som for en konvergerende linse. Bildets natur avhenger ikke av hvor langt objektet er fra den divergerende linsen, så det vil bare være ett tilfelle her.

Igjen tar vi en stråle og en vilkårlig stråle (fig. 12). Ved utgangen fra linsen har vi to divergerende stråler og , som øyet vårt bygger opp til skjæringspunktet ved punktet .

Vi må igjen bevise bildeteoremet - at punktet vil være det samme for alle stråler. Vi handler ved hjelp av de samme tre parene med like trekanter:

(12)

. (13)

Verdien av b avhenger ikke av strålespennet
, så forlengelsene av alle refrakterte stråler spenner over
skjære i et punkt - det imaginære bildet av punktet. Bildesetningen er dermed fullstendig bevist.

Husk at for en konvergerende linse fikk vi lignende formler (6) og (10) . I tilfelle av deres nevner forsvant (bildet gikk til det uendelige), og derfor skilte denne saken fundamentalt forskjellige situasjoner og .

Men for formel (13) forsvinner ikke nevneren for noen a. Derfor, for en divergerende linse er det ingen kvalitativt ulike situasjoner kildeplassering - det er bare ett tilfelle her, som vi sa ovenfor.

Hvis punktet ikke ligger på den optiske hovedaksen, er to stråler praktiske for å konstruere bildet: den ene går gjennom det optiske senteret, den andre er parallell med den optiske hovedaksen (fig. 13).

Hvis punktet ligger på den optiske hovedaksen, må den andre strålen tas vilkårlig (fig. 14).

For å finne ut hvilken linse som gir hvilket bilde, må du først huske at det fysiske hovedfenomenet som brukes til å lage en linse, er det som går gjennom mediet. Det var dette fenomenet som gjorde det mulig å lage en slik enhet som kan kontrollere retningen til lysstrømmene. Prinsippene for slik kontroll blir forklart til barn på skolen, i fysikkkurset i åttende klasse.

Definisjon av ordet linse og materialet som brukes til å lage det

Linser brukes slik at en person kan se et forstørret eller forminsket bilde av et objekt. For eksempel ved hjelp av et teleskop eller mikroskop. Derfor er denne enheten gjennomsiktig. Dette ble gjort med sikte på å se objekter slik vi egentlig er, kun endret i størrelse. Den vil ikke bli farget, forvrengt hvis dette ikke er nødvendig. Det vil si at linsen er en gjennomsiktig kropp. La oss gå videre til komponentene. Linsen består av to overflater. De kan være krumlinjede, ofte sfæriske, eller en av dem vil være krumlinjet og den andre flat. Det er fra disse planene at hvilken linse som gir hvilket bilde avhenger. Materialet for fremstilling av linser i bred hverdag er glass eller plast. Videre vil vi snakke spesifikt om glasslinser for en generell forståelse.

Inndeling i konvekse og konkave linser

Denne inndelingen avhenger av formen på linsen. Hvis linsen har en midtre som er bredere enn kantene, kalles den konveks. Hvis tvert imot midten er tynnere enn kantene, kalles en slik enhet konkav. Hva annet er viktig? Det som betyr noe er miljøet der den gjennomsiktige kroppen befinner seg. Tross alt, hvilken linse som gir hvilket bilde avhenger av brytningen i to medier - i selve linsen og i materien rundt den. Videre vil vi bare vurdere luftrom, siden linser laget av glass eller plast er høyere enn den etablerte miljøindikatoren.

konvergerende linse

La oss ta en konveks linse og sende en strøm av lys (parallelle stråler) gjennom den. Etter å ha passert gjennom overflatens plan, samles strømmen på ett punkt, og det er grunnen til at linsen kalles en konvergerende linse.

For å forstå hva slags bilde en konvergerende linse gir, og faktisk alle andre, må du huske hovedparametrene.

Viktige parametere for å forstå egenskapene til en gitt glasskropp

Hvis en linse er begrenset av to sfæriske overflater, så har kulene selvfølgelig en viss radius. Disse radiene kalles krumningsradiene, som kommer ut fra sentrene til kulene. Den rette linjen som forbinder begge sentrene kalles den optiske aksen. En tynn linse har et punkt som strålen passerer gjennom uten mye avvik fra den forrige retningen. Det kalles det optiske sentrum av linsen. Gjennom dette senteret, vinkelrett på den optiske aksen, kan man tegne vinkelrett plan. Det kalles linsens hovedplan. Det er også et punkt, som kalles hovedfokus - stedet hvor strålene samles etter å ha passert gjennom glasskroppen. Når man analyserer spørsmålet om hva slags bilde en konvergerende linse gir, er det viktig å huske at fokuset er med motsatt side fra inntreden av stråler. Med en divergerende linse er fokus imaginært.

Hvilket bilde av et objekt gir en konvergerende linse?

Det avhenger direkte av hvor langt objektet er plassert i forhold til linsen. Det blir ikke noe reelt bilde hvis et objekt plasseres mellom objektivets fokus og selve objektivet.

Bildet er imaginært, rett og sterkt forstørret. Et elementært eksempel på et slikt bilde er et forstørrelsesglass.

Hvis du plasserer objekter bak fokuset, er to alternativer mulige, men i begge tilfeller vil bildet være invertert og ekte i utgangspunktet. Forskjellen er kun i størrelse. Hvis du plasserer objekter mellom fokus og dobbeltfokus, forstørres bildet. Hvis du plasserer den bak dobbeltfokuset, vil den reduseres.

I noen tilfeller kan det hende at det ikke mottas noe bilde i det hele tatt. Som du kan se fra figuren ovenfor, hvis du plasserer objektet like ved linsens fokus, løper linjene som krysser hverandre for å gi objektets topppunkt parallelt. Følgelig er skjæringspunktet uaktuelt, fordi bildet bare kan oppnås et sted i det uendelige. Også interessant er tilfellet når et objekt er plassert på stedet for dobbeltfokus. I dette tilfellet er bildet snudd opp ned, ekte, men identisk i størrelse med originalobjektet.

På figurene er denne linsen skjematisk avbildet som et segment med piler i endene som peker utover.

divergerende linse

Logisk sett er en konkav linse divergerende. Forskjellen er at den gir et virtuelt bilde. Stråler av lys etter å ha passert det er spredt inn i forskjellige sider, så det er ikke noe faktisk bilde. Svaret på spørsmålet om hvilket bilde gir er alltid det samme. I alle fall vil bildet ikke bli invertert, det vil si rett, det vil være imaginært og redusert.

På figurene er denne linsen skjematisk avbildet som et segment med piler i endene som ser innover.

Hva er prinsippet for å bygge et bilde

Det er flere byggetrinn. Objektet hvis bilde skal bygges har et toppunkt. To linjer må trekkes fra den: en gjennom det optiske sentrum av linsen, den andre parallelt med den optiske aksen til linsen, og deretter gjennom fokuset. Skjæringspunktet mellom disse linjene vil gi toppen av bildet. Alt som trengs videre er å koble den optiske aksen og det resulterende punktet, parallelt med det opprinnelige objektet. I tilfellet når objektet er foran objektivets fokus, vil bildet være imaginært og være på samme side som objektet.

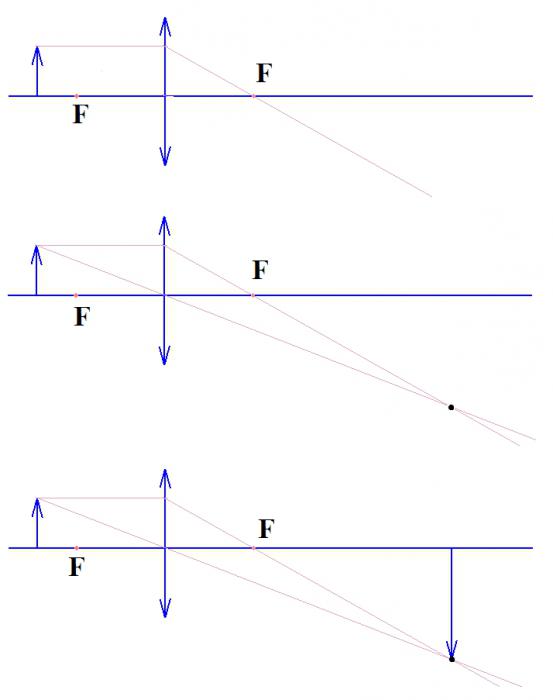
Vi husker hva slags bilde en divergerende linse gir, så vi bygger et bilde for en konkav linse, etter samme prinsipp, med bare én forskjell. Fokuset til linsen som brukes til konstruksjonen er på samme side som objektet hvis bilde må bygges.

konklusjoner

La oss oppsummere materialene ovenfor for å forstå hvilket objektiv som gir hvilket bilde. Det er klart at linsen kan øke og minke, men spørsmålene er forskjellige.

Spørsmål nummer én: hvilke linser produserer et ekte bilde? Svaret er bare kollektivt. Det er en konkav konvergerende linse som kan gi et ekte bilde.

Spørsmål nummer to: hva slags linse produserer et virtuelt bilde? Svaret er spredning, og i noen tilfeller, når objektet er mellom fokus og linse, er det kollektivt.

På fig. 22 viser de enkleste profilene til glasslinser: plankonvekse, bikonvekse (fig. 22, b), flat-konkav (fig. 22, i) og bikonkav (fig. 22, G). De to første av dem i luften er samling linser, og de to andre - spredning. Disse navnene er assosiert med det faktum at i en konvergerende linse avviker strålen, som brytes, mot den optiske aksen, og omvendt i en divergerende.

Stråler som løper parallelt med den optiske hovedaksen avbøyes bak en konvergerende linse (fig. 23, en) slik at de samles på et punkt som kalles fokus. I en divergerende linse avbøyes stråler som beveger seg parallelt med den optiske hovedaksen slik at fortsettelsene deres samles ved fokuset på siden av de innfallende strålene (fig. 23, b). Avstanden til fokusene på begge sider av en tynn linse er den samme og avhenger ikke av profilen til høyre og venstre overflate av linsen.

Ris. 22. Plankonveks ( en), bikonveks ( b), plankonkav ( i) og bikonkav ( G) linser.

Ris. 23. Banen til strålene som løper parallelt med den optiske hovedaksen i de samlende (a) og divergerende (b) linsene.

Strålen som går gjennom midten av linsen (fig. 24, en- konvergerende linse, fig. 24, b- divergerende linse), brytes ikke.

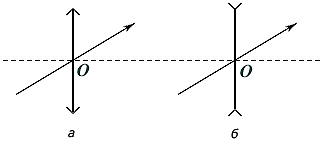
Ris. 24. Forløpet av stråler som går gjennom det optiske senteret O , i konvergerende (a) og divergerende (b) linser.

Stråler som beveger seg parallelt med hverandre, men ikke parallelt med den optiske hovedaksen, skjærer hverandre i et punkt (sidefokus) på brennplan, som går gjennom fokuset til linsen vinkelrett på den optiske hovedaksen (fig. 25, en- konvergerende linse, fig. 25, b- divergerende linse).

Ris. 25. Forløpet av parallelle stråler av stråler i samlelinsene (a) og spredningslinsene (b).

.

Når du konstruerer (fig. 26) et bilde av et punkt (for eksempel spissen av en pil) ved bruk av en konvergerende linse, sendes to stråler ut fra dette punktet: parallelt med den optiske hovedaksen og gjennom midten O linser.

Ris. 26. Bygge bilder i en konvergerende linse

Avhengig av avstanden fra pilen til linsen, kan fire typer bilder oppnås, hvis egenskaper er beskrevet i tabell 2. Når du konstruerer et bilde av et segment vinkelrett på den optiske hovedaksen, viser det seg også å være et segment vinkelrett på den optiske hovedaksen.

Når divergerende linse et bilde av et objekt kan bare være av én type - imaginær, redusert, direkte. Dette kan lett sees ved å utføre lignende konstruksjoner av enden av pilen ved hjelp av to stråler (fig. 27).

tabell 2