Hvordan finne verdien av en matrise. Egenverdier og egenvektorer til en matrise

SYSTEM AV HOMOGENE LINEÆRE LIGNINGER

Et system med homogene lineære ligninger er et formsystem

Det er klart at i dette tilfellet , fordi alle elementene i en av kolonnene i disse determinantene er lik null.

Siden de ukjente finnes av formlene , så i tilfellet når Δ ≠ 0, har systemet en unik nullløsning x = y = z= 0. Men i mange problemer er spørsmålet om et homogent system har andre løsninger enn null av interesse.

Teorem. For at et system med lineære homogene ligninger skal ha en løsning som ikke er null, er det nødvendig og tilstrekkelig at Δ ≠ 0.

Så hvis determinanten er Δ ≠ 0, så har systemet en unik løsning. Hvis Δ ≠ 0, så har systemet med lineære homogene ligninger et uendelig antall løsninger.

Eksempler.

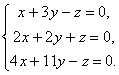
Egenvektorer og matriseegenverdier

La det gis en kvadratisk matrise , X er en matrisekolonne hvis høyde sammenfaller med rekkefølgen til matrisen EN. .

I mange problemer må man vurdere ligningen for X

hvor λ er et tall. Det er klart at for enhver λ har denne ligningen en nullløsning.

Tallet λ som denne ligningen har løsninger som ikke er null kalles egenverdi matriser EN, a X for slikt kalles λ egen vektor matriser EN.

La oss finne egenvektoren til matrisen EN. Fordi det E∙X=X, så kan matriseligningen skrives om som eller . I utvidet form kan denne ligningen skrives om som et system av lineære ligninger. Egentlig .

Og derfor

Så vi har et system med homogene lineære ligninger for å bestemme koordinatene x 1, x2, x 3 vektor X. For at systemet skal ha løsninger som ikke er null, er det nødvendig og tilstrekkelig at determinanten til systemet er lik null, dvs.

Dette er en 3. grads ligning med hensyn til λ. Det heter karakteristisk ligning matriser EN og tjener til å bestemme egenverdiene λ.

Hver egenverdi λ tilsvarer en egenvektor X, hvis koordinater bestemmes fra systemet ved den tilsvarende verdien av λ.

Eksempler.

VEKTORALGEBRA. VEKTOR KONSEPT

Når du studerer ulike grener av fysikk, er det mengder som er fullstendig bestemt ved å sette deres numeriske verdier, for eksempel lengde, areal, masse, temperatur, etc. Slike verdier kalles skalar. Men i tillegg til dem er det også mengder, for bestemmelsen av hvilke, i tillegg til den numeriske verdien, det også er nødvendig å vite retningen deres i rommet, for eksempel kraften som virker på kroppen, hastigheten og akselerasjonen. av kroppen når den beveger seg i rommet, magnetfeltstyrken på et gitt punkt i rommet og etc. Slike mengder kalles vektormengder.

La oss introdusere en streng definisjon.

Retningsbestemt segment La oss kalle et segment, i forhold til endene som det er kjent hvilken av dem som er den første og hvilken som er den andre.

Vektor et rettet segment kalles, som har en viss lengde, dvs. Dette er et segment av en viss lengde, der ett av punktene som begrenser det tas som begynnelsen, og det andre - som slutten. Hvis en EN er begynnelsen av vektoren, B er slutten, så er vektoren betegnet med symbolet, i tillegg er vektoren ofte betegnet med en enkelt bokstav . På figuren er vektoren indikert med et segment, og retningen med en pil.

modul eller lengde vektor kalles lengden på det rettede segmentet som definerer det. Angitt med || eller ||.

Den såkalte nullvektoren, hvis begynnelse og slutt faller sammen, vil også bli referert til som vektorer. Det er merket. Nullvektoren har ingen bestemt retning og dens modul er lik null ||=0.

Vektorer og kalles kollineær hvis de er plassert på samme linje eller på parallelle linjer. I dette tilfellet, hvis vektorene og er likt rettet, vil vi skrive , motsatt.

Vektorer plassert på rette linjer parallelt med samme plan kalles koplanar.

To vektorer og kalles lik hvis de er collineære, har samme retning og er like lange. Skriv i dette tilfellet.

Det følger av definisjonen av vektorlikhet at en vektor kan flyttes parallelt med seg selv ved å plassere sin opprinnelse på et hvilket som helst punkt i rommet.

For eksempel.

LINEÆRE OPERASJONER PÅ VEKTORER

1. Multiplisere en vektor med et tall.

   Produktet av en vektor med et tall λ er en ny vektor slik at:

   Produktet av en vektor og et tall λ er betegnet med .

   

   For eksempel, er en vektor som peker i samme retning som vektoren og har en lengde som er halvparten av vektoren.

   Den angitte operasjonen har følgende eiendommer:

2. Addisjon av vektorer.

   La og være to vilkårlige vektorer. Ta et vilkårlig poeng O og konstruer en vektor. Etter det, fra poenget EN sett til side vektoren. Vektoren som forbinder begynnelsen av den første vektoren med slutten av den andre kalles sum av disse vektorene og er betegnet .

   

   Den formulerte definisjonen av vektoraddisjon kalles parallellogramregel, siden samme sum av vektorer kan oppnås som følger. Sett til side fra poenget O vektorer og . Konstruer et parallellogram på disse vektorene OABC. Siden vektorene, så vektoren, som er diagonalen til parallellogrammet trukket fra toppunktet O, vil åpenbart være summen av vektorer.

   

   Det er enkelt å sjekke følgende vektoraddisjonsegenskaper.

3. Forskjell mellom vektorer.

   En vektor kollineær til en gitt vektor, lik lengde og motsatt rettet, kalles motsatte vektor for en vektor og er betegnet med . Den motsatte vektoren kan betraktes som resultatet av vektormultiplikasjon med tallet λ = –1: .

Hvordan sette inn matematiske formler på nettstedet?

Hvis du noen gang trenger å legge til en eller to matematiske formler på en nettside, er den enkleste måten å gjøre dette på som beskrevet i artikkelen: matematiske formler settes enkelt inn på nettstedet i form av bilder som Wolfram Alpha genererer automatisk. I tillegg til enkelhet, vil denne universelle metoden bidra til å forbedre synligheten til nettstedet i søkemotorer. Det har fungert lenge (og jeg tror det vil fungere for alltid), men det er moralsk utdatert.

Hvis du derimot stadig bruker matematiske formler på nettstedet ditt, anbefaler jeg at du bruker MathJax, et spesielt JavaScript-bibliotek som viser matematisk notasjon i nettlesere som bruker MathML, LaTeX eller ASCIIMathML-markering.

Det er to måter å begynne å bruke MathJax på: (1) ved hjelp av en enkel kode kan du raskt koble et MathJax-skript til nettstedet ditt, som automatisk lastes fra en ekstern server til rett tid (liste over servere); (2) last opp MathJax-skriptet fra en ekstern server til serveren din og koble det til alle sidene på nettstedet ditt. Den andre metoden er mer komplisert og tidkrevende og vil tillate deg å øke hastigheten på lasting av sidene til nettstedet ditt, og hvis den overordnede MathJax-serveren blir midlertidig utilgjengelig av en eller annen grunn, vil dette ikke påvirke ditt eget nettsted på noen måte. Til tross for disse fordelene, valgte jeg den første metoden, da den er enklere, raskere og ikke krever tekniske ferdigheter. Følg mitt eksempel, og innen 5 minutter vil du kunne bruke alle funksjonene til MathJax på nettstedet ditt.

Du kan koble til MathJax-biblioteksskriptet fra en ekstern server ved å bruke to kodealternativer hentet fra MathJax hovednettsted eller fra dokumentasjonssiden:

Ett av disse kodealternativene må kopieres og limes inn i koden til nettsiden din, helst mellom taggene og eller rett etter taggen . I henhold til det første alternativet laster MathJax raskere og bremser siden mindre. Men det andre alternativet sporer og laster automatisk de nyeste versjonene av MathJax. Hvis du setter inn den første koden, må den oppdateres med jevne mellomrom. Hvis du limer inn den andre koden, vil sidene lastes saktere, men du trenger ikke å overvåke MathJax-oppdateringer konstant.

Den enkleste måten å koble til MathJax på er i Blogger eller WordPress: i nettstedets kontrollpanel, legg til en widget designet for å sette inn tredjeparts JavaScript-kode, kopier den første eller andre versjonen av lastekoden presentert ovenfor inn i den, og plasser widgeten nærmere til begynnelsen av malen (forresten, dette er ikke i det hele tatt nødvendig, siden MathJax-skriptet lastes asynkront). Det er alt. Lær nå MathML-, LaTeX- og ASCIIMathML-markeringssyntaksen, og du er klar til å bygge inn matematiske formler på nettsidene dine.

Enhver fraktal er bygget i henhold til en bestemt regel, som konsekvent brukes et ubegrenset antall ganger. Hver slik tid kalles en iterasjon.

Den iterative algoritmen for å konstruere en Menger-svamp er ganske enkel: den originale kuben med side 1 er delt av plan parallelt med flatene i 27 like terninger. En sentral kube og 6 terninger ved siden av den langs ansiktene fjernes fra den. Det viser seg et sett bestående av 20 gjenværende mindre kuber. Gjør vi det samme med hver av disse kubene, får vi et sett bestående av 400 mindre terninger. Hvis vi fortsetter denne prosessen på ubestemt tid, får vi Menger-svampen.

". Den første delen inneholder bestemmelsene som er minimalt nødvendige for å forstå kjemometri, og den andre delen inneholder fakta som du trenger å vite for en dypere forståelse av metodene for multivariat analyse. Presentasjonen er illustrert med eksempler laget i Excel-arbeidsboken Matrix.xls som følger med dette dokumentet.

Lenker til eksempler er plassert i teksten som Excel-objekter. Disse eksemplene er av abstrakt karakter; de er på ingen måte knyttet til problemene med analytisk kjemi. Eksempler på bruk av matrisealgebra i kjemometri er diskutert i andre tekster viet ulike kjemometriske anvendelser.

De fleste målingene utført i analytisk kjemi er ikke direkte, men indirekte. Dette betyr at i forsøket, i stedet for verdien til ønsket analytt C (konsentrasjon), oppnås en annen verdi x(signal) relatert til men ikke lik C, dvs. x(C) ≠ C. Som regel, typen avhengighet x(C) er ikke kjent, men heldigvis i analytisk kjemi er de fleste målinger proporsjonale. Dette betyr at som konsentrasjonen av C in en ganger, vil signalet X øke like mye, dvs. x(en C) = en x(C). I tillegg er signalene også additive, slik at signalet fra en prøve som inneholder to stoffer med konsentrasjoner C 1 og C 2 vil være lik summen av signalene fra hver komponent, d.v.s. x(C1 + C2) = x(C1)+ x(C2). Proporsjonalitet og additivitet gir til sammen linearitet. Mange eksempler kan gis for å illustrere linearitetsprinsippet, men det er nok å nevne to av de mest slående eksemplene - kromatografi og spektroskopi. Den andre egenskapen som er iboende i eksperimentet i analytisk kjemi er multikanal. Moderne analyseutstyr måler signaler for mange kanaler samtidig. For eksempel måles intensiteten av lystransmisjon for flere bølgelengder på en gang, dvs. spektrum. Derfor har vi i eksperimentet å gjøre med en rekke signaler x 1 , x 2 ,...., x n som karakteriserer settet med konsentrasjoner C 1 , C 2 , ..., C m av stoffer som er tilstede i systemet som studeres.

Ris. 1 spektra

Så det analytiske eksperimentet er preget av linearitet og flerdimensjonalitet. Derfor er det praktisk å betrakte eksperimentelle data som vektorer og matriser og manipulere dem ved å bruke apparatet til matrisealgebra. Fruktbarheten av denne tilnærmingen er illustrert av eksemplet vist i , som viser tre spektre tatt for 200 bølgelengder fra 4000 til 4796 cm–1. Den første ( x 1) og andre ( x 2) spektrene ble oppnådd for standardprøver der konsentrasjonene av to stoffer A og B er kjent: i den første prøven [A] = 0,5, [B] = 0,1, og i den andre prøven [A] = 0,2, [ B] = 0,6. Hva kan sies om en ny, ukjent prøve, hvis spektrum er angitt x 3 ?

Tenk på tre eksperimentelle spektra x 1 , x 2 og x 3 som tre vektorer med dimensjon 200. Ved hjelp av lineær algebra kan man enkelt vise det x 3 = 0.1 x 1 +0.3 x 2 , så den tredje prøven inneholder åpenbart bare stoffene A og B i konsentrasjoner [A] = 0,5×0,1 + 0,2×0,3 = 0,11 og [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Grunnleggende informasjon

1.1 Matriser

Matrise kalt en rektangulær talltabell, for eksempel

Ris. 2 Matrise

Matriser er merket med store, fete bokstaver ( EN), og deres elementer - med de tilsvarende små bokstavene med indekser, dvs. en ij . Den første indeksen nummererer radene og den andre nummererer kolonnene. I kjemometri er det vanlig å angi maksimalverdien av indeksen med samme bokstav som selve indeksen, men med store bokstaver. Derfor matrisen EN kan også skrives som ( en ij , Jeg = 1,..., Jeg; j = 1,..., J). For eksempelmatrisen Jeg = 4, J= 3 og en 23 = −7.5.

Par med tall Jeg og J kalles matrisens dimensjon og betegnes som Jeg× J. Et eksempel på en matrise i kjemometri er et sett med spektre oppnådd for Jeg prøver på J bølgelengder.

1.2. De enkleste operasjonene med matriser

Matriser kan multiplisere med tall. I dette tilfellet multipliseres hvert element med dette tallet. For eksempel -

Ris. 3 Multiplisere en matrise med et tall

To matriser med samme dimensjon kan være elementmessig brette og trekke fra. For eksempel,

Ris. 4 Matrisetillegg

Som et resultat av multiplikasjon med et tall og addisjon, oppnås en matrise med samme dimensjon.

En nullmatrise er en matrise som består av nuller. Det er utpekt O. Det er åpenbart det EN+O = EN, EN−EN = O og 0 EN = O.

Matrisen kan transponere. Under denne operasjonen blir matrisen snudd, dvs. rader og kolonner byttes. Transponering er indikert med en bindestrek, EN" eller indeks EN t . Således, hvis EN = {en ij , Jeg = 1,..., Jeg; j = 1,...,J), deretter EN t = ( en ji , j = 1,...,J; i = 1,..., Jeg). For eksempel

Ris. 5 Matrisetransponering

Det er tydelig at ( EN t) t = EN, (EN+B) t = A t + B t .

1.3. Matrisemultiplikasjon

Matriser kan multiplisere, men bare hvis de har de riktige dimensjonene. Hvorfor det er slik vil fremgå av definisjonen. Matriseprodukt EN, dimensjon Jeg× K, og matriser B, dimensjon K× J, kalles matrisen C, dimensjon Jeg× J, hvis elementer er tall

Altså for produktet AB det er nødvendig at antall kolonner i venstre matrise EN var lik antall rader i den høyre matrisen B. Eksempel på matriseprodukt -

Fig.6 Produkt av matriser

Matrisemultiplikasjonsregelen kan formuleres som følger. For å finne et element i en matrise C står i krysset Jeg-te linje og j-th kolonne ( c ij) må multipliseres element for element Jeg-te rad i den første matrisen EN på j-th kolonne av den andre matrisen B og legg sammen alle resultatene. Så i eksemplet som vises, oppnås elementet fra den tredje raden og den andre kolonnen som summen av de elementmessige produktene i den tredje raden EN og andre kolonne B

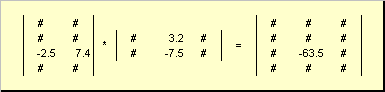
Fig.7 Element av produktet av matriser

Produktet av matriser avhenger av rekkefølgen, dvs. AB ≠ BA, i det minste av dimensjonale årsaker. Det sies å være ikke-kommutativt. Produktet av matriser er imidlertid assosiativt. Det betyr at ABC = (AB)C = EN(f.Kr). Dessuten er den også distributiv, dvs. EN(B+C) = AB+AC. Det er åpenbart det AO = O.

1.4. Firkantede matriser

Hvis antall kolonner i en matrise er lik antall rader ( Jeg = J=N), så kalles en slik matrise kvadrat. I denne delen vil vi kun vurdere slike matriser. Blant disse matrisene kan man skille ut matriser med spesielle egenskaper.

Ensom matrise (betegnet Jeg og noen ganger E) er en matrise der alle elementene er lik null, bortsett fra de diagonale, som er lik 1, dvs.

Åpenbart AI = IA = EN.

Matrisen kalles diagonal, hvis alle dens elementer, bortsett fra de diagonale ( en ii) er lik null. For eksempel

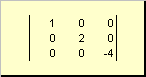
Ris. 8 Diagonal matrise

Matrise EN kalt toppen trekantet, hvis alle dens elementer som ligger under diagonalen er lik null, dvs. en ij= 0, kl Jeg>j. For eksempel

Ris. 9 Øvre trekantmatrise

Den nedre trekantede matrisen er definert på samme måte.

Matrise EN kalt symmetrisk, hvis EN t = EN. Med andre ord en ij = en ji. For eksempel

Ris. 10 Symmetrisk matrise

Matrise EN kalt ortogonal, hvis

EN t EN = AA t = Jeg.

Matrisen kalles vanlig hvis

1.5. Spor og determinant

Følgende kvadratisk matrise EN(betegnet Tr( EN) eller Sp( EN)) er summen av de diagonale elementene,

For eksempel,

Ris. 11 Matrisesporing

Det er åpenbart det

Sp(α EN) = α Sp( EN) og

Sp( EN+B) = Sp( EN)+ Sp( B).

Det kan vises

Sp( EN) = Sp( EN t), Sp( Jeg) = N,

og også det

Sp( AB) = Sp( BA).

En annen viktig egenskap ved en kvadratisk matrise er dens avgjørende faktor(betegnet med det( EN)). Definisjonen av determinanten i det generelle tilfellet er ganske komplisert, så vi starter med det enkleste alternativet - matrisen EN dimensjon (2×2). Deretter

For en (3×3) matrise vil determinanten være lik

I tilfelle av en matrise ( N× N) determinanten beregnes som summen 1 2 3 ... N= N! vilkår, som hver er lik

Indekser k 1 , k 2 ,..., k N er definert som alle mulige ordnede permutasjoner r tall i settet (1, 2, ... , N). Beregningen av matrisedeterminanten er en kompleks prosedyre, som i praksis utføres ved hjelp av spesielle programmer. For eksempel,

Ris. 12 Matrisedeterminant

Vi legger bare merke til de åpenbare egenskapene:

det( Jeg) = 1, det( EN) = det( EN t),

det( AB) = det( EN)det( B).

1.6. Vektorer

Hvis matrisen bare har én kolonne ( J= 1), så kalles et slikt objekt vektor. Mer presist, en kolonnevektor. For eksempel

Matriser som består av én rad kan også vurderes, for eksempel

Dette objektet er også en vektor, men rad vektor. Når man analyserer data er det viktig å forstå hvilke vektorer vi har å gjøre med – kolonner eller rader. Så spekteret tatt for en prøve kan betraktes som en radvektor. Deretter bør settet med spektralintensiteter ved en eller annen bølgelengde for alle prøver behandles som en kolonnevektor.

Dimensjonen til en vektor er antall elementer.

Det er klart at enhver kolonnevektor kan transformeres til en radvektor ved transposisjon, dvs.

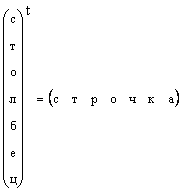
I de tilfellene hvor formen til en vektor ikke er spesifikt spesifisert, men bare en vektor sies, så betyr de en kolonnevektor. Vi vil også følge denne regelen. En vektor er merket med en liten direkte fet bokstav. En nullvektor er en vektor som alle elementer er lik null. Det er betegnet 0 .

1.7. De enkleste operasjonene med vektorer

Vektorer kan legges til og multipliseres med tall på samme måte som matriser. For eksempel,

Ris. 13 Operasjoner med vektorer

To vektorer x og y kalt kollineær, hvis det er et tall α slik at

1.8. Produkter av vektorer

To vektorer av samme dimensjon N kan multipliseres. La det være to vektorer x = (x 1 , x 2 ,...,x N) t og y = (y 1 , y 2 ,...,y N) t. Guidet av multiplikasjonsregelen "rad for kolonne", kan vi lage to produkter fra dem: x t y og xy t . Første arbeid

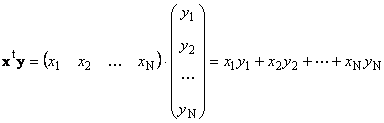
kalt skalar eller innvendig. Resultatet er et tall. Den bruker også notasjonen ( x,y)= x t y. For eksempel,

Ris. 14 Indre (skalar) produkt

Andre arbeid

kalt utvendig. Resultatet er en dimensjonsmatrise ( N× N). For eksempel,

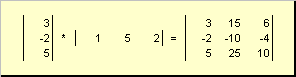
Ris. 15 Ytre produkt

Vektorer hvis skalarprodukt er lik null kalles ortogonal.

1.9. Vektornorm

Skalarproduktet av en vektor med seg selv kalles en skalar firkant. Denne verdien

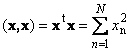
definerer en firkant lengde vektor x. For å betegne lengde (også kalt normen vektor) brukes notasjonen

For eksempel,

Ris. 16 Vektornorm

Enhetslengdevektor (|| x|| = 1) kalles normalisert. Ikke null vektor ( x ≠ 0 ) kan normaliseres ved å dele den på lengden, dvs. x = ||x|| (x/||x||) = ||x|| e. Her e = x/||x|| er en normalisert vektor.

Vektorer kalles ortonormale hvis de alle er normaliserte og parvis ortogonale.

1.10. Vinkel mellom vektorer

Det skalære produktet definerer og hjørneφ mellom to vektorer x og y

Hvis vektorene er ortogonale, så er cosφ = 0 og φ = π/2, og hvis de er kollineære, så er cosφ = 1 og φ = 0.

1.11. Vektorrepresentasjon av en matrise

Hver matrise EN størrelse Jeg× J kan representeres som et sett med vektorer

Her hver vektor en j er j-th kolonne og rad vektor b Jeg er Jeg-te rad i matrisen EN

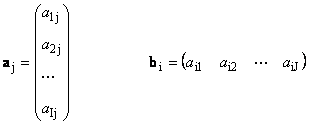
1.12. Lineært avhengige vektorer

Vektorer av samme dimensjon ( N) kan legges til og multipliseres med et tall, akkurat som matriser. Resultatet er en vektor med samme dimensjon. La det være flere vektorer av samme dimensjon x 1 , x 2 ,...,x K og samme antall tall α α 1 , α 2 ,...,α K. Vektor

y= α 1 x 1 + α 2 x 2 +...+a K x K

kalt lineær kombinasjon vektorer x k .

Hvis det er slike tall som ikke er null α k ≠ 0, k = 1,..., K, hva y = 0 , så et slikt sett med vektorer x k kalt lineært avhengig. Ellers kalles vektorene lineært uavhengige. For eksempel vektorer x 1 = (2, 2) t og x 2 = (−1, −1) t er lineært avhengige, siden x 1 +2x 2 = 0

1.13. Matriserangering

Vurder et sett med K vektorer x 1 , x 2 ,...,x K dimensjoner N. Rangeringen til dette systemet av vektorer er det maksimale antallet lineært uavhengige vektorer. For eksempel i settet

det er bare to lineært uavhengige vektorer, for eksempel x 1 og x 2, så rangeringen er 2.

Selvfølgelig, hvis det er flere vektorer i settet enn deres dimensjon ( K>N), så er de nødvendigvis lineært avhengige.

Matriserangering(angitt med rang) EN)) er rangeringen til systemet av vektorer det består av. Selv om enhver matrise kan representeres på to måter (kolonnevektorer eller radvektorer), påvirker ikke dette rangeringsverdien, siden

1.14. invers matrise

kvadratisk matrise EN kalles ikke-degenerert hvis den har en unik omvendt matrise EN-1 , bestemt av forholdene

AA −1 = EN −1 EN = Jeg.

Den inverse matrisen eksisterer ikke for alle matriser. En nødvendig og tilstrekkelig betingelse for ikke-degenerasjon er

det( EN) ≠ 0 eller rang( EN) = N.

Matriseinversjon er en kompleks prosedyre som det finnes spesielle programmer for. For eksempel,

Ris. 17 Matriseinversjon

Vi gir formler for det enkleste tilfellet - matriser 2 × 2

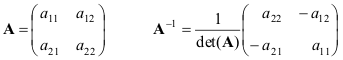
Hvis matriser EN og B er ikke-degenererte, da

(AB) −1 = B −1 EN −1 .

1.15. Pseudo-invers matrise

Hvis matrisen EN er degenerert og den inverse matrisen ikke eksisterer, så kan man i noen tilfeller bruke pseudo-invers matrise, som er definert som en slik matrise EN+ det

AA + EN = EN.

Den pseudo-inverse matrisen er ikke den eneste, og dens form avhenger av konstruksjonsmetoden. For en rektangulær matrise kan du for eksempel bruke Moore-Penrose-metoden.

Hvis antall kolonner er mindre enn antall rader, da

EN + =(EN t EN) −1 EN t

For eksempel,

Ris. 17a Pseudomatriseinversjon

Hvis antall kolonner er større enn antall rader, da

EN + =EN t ( AA t) −1

1.16. Multiplikasjon av en vektor med en matrise

Vektor x kan multipliseres med en matrise EN passende dimensjon. I dette tilfellet multipliseres kolonnevektoren til høyre Øks, og vektorstrengen er til venstre x t EN. Hvis dimensjonen til vektoren J, og dimensjonen til matrisen Jeg× J da er resultatet en vektor av dimensjon Jeg. For eksempel,

Ris. 18 Vektor-matrise multiplikasjon

Hvis matrisen EN- torget ( Jeg× Jeg), deretter vektoren y = Øks har samme dimensjon som x. Det er åpenbart det

EN(α 1 x 1 + α 2 x 2) = α 1 Øks 1 + α 2 Øks 2 .

Derfor kan matriser betraktes som lineære transformasjoner av vektorer. Spesielt x = x, Okse = 0 .

2. Ytterligere informasjon

2.1. Systemer av lineære ligninger

La EN- matrisestørrelse Jeg× J, a b- dimensjonsvektor J. Tenk på ligningen

Øks = b

med hensyn til vektoren x, dimensjoner Jeg. I hovedsak er dette et system av Jeg lineære ligninger med J ukjent x 1 ,...,x J. En løsning finnes hvis og bare hvis

rang( EN) = rangering( B) = R,

hvor B er den utvidede dimensjonsmatrisen Jeg×( J+1) som består av matrisen EN, polstret med en søyle b, B = (EN b). Ellers er ligningene inkonsekvente.

Hvis en R = Jeg = J, da er løsningen unik

x = EN −1 b.

Hvis en R < Jeg, så er det mange forskjellige løsninger som kan uttrykkes i form av en lineær kombinasjon J−R vektorer. System av homogene ligninger Øks = 0 med en kvadratisk matrise EN (N× N) har en ikke-triviell løsning ( x ≠ 0 ) hvis og bare hvis det( EN) = 0. Hvis R= rangering( EN)<N, så er det N−R lineært uavhengige løsninger.

2.2. Bilineære og kvadratiske former

Hvis en EN er en kvadratisk matrise, og x og y- vektorer av den tilsvarende dimensjonen, deretter skalarproduktet av formen x t Ja kalt bilineær formen definert av matrisen EN. På x = y uttrykk x t Øks kalt kvadratisk form.

2.3. Positive bestemte matriser

kvadratisk matrise EN kalt positiv bestemt, hvis for en vektor som ikke er null x ≠ 0 ,

x t Øks > 0.

De negativ (x t Øks < 0), ikke-negativ (x t Øks≥ 0) og ikke-positive (x t Øks≤ 0) visse matriser.

2.4. Kolesky nedbrytning

Hvis den symmetriske matrisen EN er positiv bestemt, så er det en unik trekantmatrise U med positive elementer, for hvilke

EN = U t U.

For eksempel,

Ris. 19 Kolesky nedbrytning

2.5. polar nedbrytning

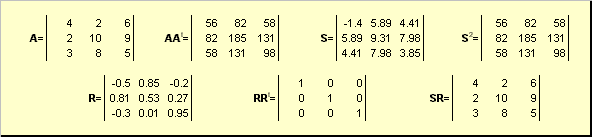
La EN er en ikke-degenerert kvadratisk matrise av dimensjon N× N. Så er det en unik polar opptreden

EN = SR,

hvor S er en ikke-negativ symmetrisk matrise, og R er en ortogonal matrise. matriser S og R kan defineres eksplisitt:

S 2 = AA t eller S = (AA t) ½ og R = S −1 EN = (AA t) −½ EN.

For eksempel,

Ris. 20 Polar nedbrytning

Hvis matrisen EN er degenerert, så er ikke nedbrytningen unik - nemlig: S fortsatt alene, men R det kan være mange. Polar dekomponering representerer en matrise EN som en kompresjon/stretch-kombinasjon S og snu R.

2.6. Egenvektorer og egenverdier

La EN er en kvadratisk matrise. Vektor v kalt egen vektor matriser EN, hvis

Av = λ v,

hvor tallet λ kalles egenverdi matriser EN. Dermed transformasjonen som matrisen utfører EN over vektor v, reduseres til en enkel strekking eller kompresjon med en faktor λ. Egenvektoren bestemmes frem til multiplikasjon med konstanten α ≠ 0, dvs. hvis v er en egenvektor, så α v er også en egenvektor.

2.7. Egenverdier

Ved matrisen EN, dimensjon ( N× N) kan ikke være større enn N egenverdier. De tilfredsstiller karakteristisk ligning

det( EN − λ Jeg) = 0,

som er en algebraisk ligning N-te orden. Spesielt for en 2×2 matrise har den karakteristiske ligningen formen

For eksempel,

Ris. 21 Egenverdier

Sett med egenverdier λ 1 ,..., λ N matriser EN kalt spektrum EN.

Spekteret har ulike egenskaper. Spesielt

det( EN) = λ 1×...×λ N, Sp( EN) = λ 1 +...+λ N.

Egenverdiene til en vilkårlig matrise kan være komplekse tall, men hvis matrisen er symmetrisk ( EN t = EN), så er egenverdiene reelle.

2.8. Egenvektorer

Ved matrisen EN, dimensjon ( N× N) kan ikke være større enn N egenvektorer, som hver tilsvarer sin egen verdi. For å bestemme egenvektoren v n du må løse et system med homogene ligninger

(EN − λ n Jeg)v n = 0 .

Den har en ikke-triviell løsning fordi det( EN-λ n Jeg) = 0.

For eksempel,

Ris. 22 egenvektorer

Egenvektorene til en symmetrisk matrise er ortogonale.

En egenvektor til en kvadratisk matrise er en som, multiplisert med en gitt matrise, resulterer i en kollineær vektor. Med enkle ord, når en matrise multipliseres med en egenvektor, forblir sistnevnte den samme, men multiplisert med et eller annet tall.

Definisjon

En egenvektor er en ikke-null vektor V, som, når multiplisert med en kvadratisk matrise M, blir seg selv, økt med et eller annet tall λ. I algebraisk notasjon ser dette slik ut:

M × V = λ × V,

hvor λ er en egenverdi til matrisen M.

La oss vurdere et numerisk eksempel. For enkelhets skyld vil tallene i matrisen være atskilt med et semikolon. La oss si at vi har en matrise:

• M = 0; fire;
• 6; 10.

La oss multiplisere det med en kolonnevektor:

• V = -2;

Når vi multipliserer en matrise med en kolonnevektor, får vi også en kolonnevektor. I strengt matematisk språk vil formelen for å multiplisere en 2 × 2 matrise med en kolonnevektor se slik ut:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 betyr elementet i matrisen M, som står i første rad og første kolonne, og M22 er elementet som ligger i andre rad og andre kolonne. For matrisen vår er disse elementene M11 = 0, M12 = 4, M21 = 6, M22 10. For en kolonnevektor er disse verdiene V11 = –2, V21 = 1. I følge denne formelen får vi følgende resultat av produktet av en kvadratisk matrise med en vektor:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

For enkelhets skyld skriver vi kolonnevektoren i en rad. Så vi har multiplisert kvadratmatrisen med vektoren (-2; 1), noe som resulterer i vektoren (4; -2). Det er klart at dette er den samme vektoren multiplisert med λ = -2. Lambda i dette tilfellet angir en egenverdi til matrisen.

En egenvektor til en matrise er en kollineær vektor, det vil si et objekt som ikke endrer sin posisjon i rommet når det multipliseres med en matrise. Konseptet med kollinearitet i vektoralgebra ligner på begrepet parallellisme i geometri. I geometrisk tolkning er kollineære vektorer parallellrettede segmenter av forskjellig lengde. Siden Euklids tid vet vi at en enkelt linje har et uendelig antall linjer parallelle med seg, så det er logisk å anta at hver matrise har et uendelig antall egenvektorer.

Fra forrige eksempel kan man se at både (-8; 4), og (16; -8), og (32, -16) kan være egenvektorer. Alle disse er kollineære vektorer som tilsvarer egenverdien λ = -2. Når vi multipliserer den opprinnelige matrisen med disse vektorene, vil vi fortsatt få en vektor som et resultat, som avviker fra originalen med 2 ganger. Det er derfor, når du løser problemer for å finne en egenvektor, er det nødvendig å finne bare lineært uavhengige vektorobjekter. Oftest, for en n × n matrise, er det n-te antall egenvektorer. Kalkulatoren vår er designet for analyse av andreordens kvadratmatriser, så nesten alltid to egenvektorer vil bli funnet som et resultat, bortsett fra når de faller sammen.

I eksemplet ovenfor kjente vi på forhånd egenvektoren til den opprinnelige matrisen og bestemte lambdatallet visuelt. Men i praksis skjer alt omvendt: i begynnelsen er det egenverdier og først da egenvektorer.

Løsningsalgoritme

La oss se på den opprinnelige matrisen M igjen og prøve å finne begge dens egenvektorer. Så matrisen ser slik ut:

• M = 0; fire;
• 6; 10.

Til å begynne med må vi bestemme egenverdien λ, som vi må beregne determinanten for følgende matrise for:

• (0 - λ); fire;
• 6; (10 − λ).

Denne matrisen oppnås ved å trekke den ukjente λ fra elementene på hoveddiagonalen. Determinanten bestemmes av standardformelen:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Siden vektoren vår ikke må være null, tar vi den resulterende ligningen som lineært avhengig og likestiller vår determinant detA til null.

(0 − λ) × (10 − λ) − 24 = 0

La oss åpne parentesene og få den karakteristiske ligningen til matrisen:

λ 2 − 10λ − 24 = 0

Dette er en standard andregradsligning som må løses i form av diskriminanten.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Roten til diskriminanten er sqrt(D) = 14, så λ1 = -2, λ2 = 12. Nå for hver lambda-verdi må vi finne en egenvektor. La oss uttrykke koeffisientene til systemet for λ = -2.

• M - λ × E = 2; fire;
• 6; 12.

I denne formelen er E identitetsmatrisen. Basert på den oppnådde matrisen, komponerer vi et system med lineære ligninger:

2x + 4y = 6x + 12y

hvor x og y er elementer i egenvektoren.

La oss samle alle X-ene til venstre og alle Y-ene til høyre. Åpenbart - 4x = 8y. Del uttrykket med - 4 og få x = -2y. Nå kan vi bestemme den første egenvektoren til matrisen ved å ta alle verdier av de ukjente (husk om uendeligheten av lineært avhengige egenvektorer). La oss ta y = 1, så x = -2. Derfor ser den første egenvektoren ut som V1 = (–2; 1). Gå tilbake til begynnelsen av artikkelen. Det var dette vektorobjektet vi multipliserte matrisen med for å demonstrere konseptet med en egenvektor.

La oss nå finne egenvektoren for λ = 12.

• M - X x E = -12; fire
• 6; -2.

La oss komponere det samme systemet med lineære ligninger;

• -12x + 4y = 6x - 2y
• -18x = -6y
• 3x=y.

La oss nå ta x = 1, derav y = 3. Dermed ser den andre egenvektoren ut som V2 = (1; 3). Når du multipliserer den opprinnelige matrisen med denne vektoren, vil resultatet alltid være den samme vektoren multiplisert med 12. Dette fullfører løsningsalgoritmen. Nå vet du hvordan du manuelt definerer en egenvektor til en matrise.

• avgjørende faktor;
• spor, det vil si summen av elementene på hoveddiagonalen;
• rangering, dvs. maksimalt antall lineært uavhengige rader/kolonner.

Programmet fungerer i henhold til algoritmen ovenfor, og minimerer løsningsprosessen. Det er viktig å påpeke at i programmet er lambdaen merket med bokstaven "c". La oss se på et numerisk eksempel.

Program eksempel

La oss prøve å definere egenvektorer for følgende matrise:

• M=5; 1. 3;
• 4; 14.

La oss legge inn disse verdiene i cellene på kalkulatoren og få svaret i følgende skjema:

• Matriserangering: 2;
• Matrisedeterminant: 18;
• Matrisespor: 19;
• Egenvektorberegning: c 2 − 19,00c + 18,00 (karakteristisk ligning);
• Egenvektorberegning: 18 (første lambdaverdi);
• Egenvektorberegning: 1 (andre lambdaverdi);
• Ligningssystem av vektor 1: -13x1 + 13y1 = 4x1 − 4y1;
• Vektor 2 ligningssystem: 4x1 + 13y1 = 4x1 + 13y1;
• Egenvektor 1: (1; 1);
• Egenvektor 2: (-3,25; 1).

Dermed har vi fått to lineært uavhengige egenvektorer.

Konklusjon

Lineær algebra og analytisk geometri er standardfag for enhver nybegynner i ingeniørfag. Et stort antall vektorer og matriser er skremmende, og det er lett å gjøre feil i slike tungvinte beregninger. Programmet vårt lar studentene sjekke beregningene sine eller automatisk løse problemet med å finne en egenvektor. Det er andre lineære algebrakalkulatorer i vår katalog, bruk dem i studiet eller arbeidet ditt.

Diagonal-type matriser er enklest ordnet. Spørsmålet oppstår om det er mulig å finne et grunnlag der matrisen til en lineær operator ville ha en diagonal form. Et slikt grunnlag finnes.
La et lineært rom R n og en lineær operator A som virker i det gis; i dette tilfellet tar operatøren A R n inn i seg selv, det vil si A:R n → R n .

Definisjon. En vektor som ikke er null kalles en egenvektor til operatoren A hvis operatoren A oversettes til en vektor som er kollineær til den, det vil si . Tallet λ kalles egenverdien eller egenverdien til operatoren A som tilsvarer egenvektoren.
Vi legger merke til noen egenskaper til egenverdier og egenvektorer.
1. Enhver lineær kombinasjon av egenvektorer av operatoren A som svarer til samme egenverdi λ er en egenvektor med samme egenverdi.
2. Egenvektorer operator A med parvis distinkte egenverdier λ 1 , λ 2 , …, λ m er lineært uavhengige.
3. Hvis egenverdiene λ 1 =λ 2 = λ m = λ, så tilsvarer egenverdien λ ikke mer enn m lineært uavhengige egenvektorer.

Så hvis det er n lineært uavhengige egenvektorer tilsvarende forskjellige egenverdier λ 1 , λ 2 , …, λ n , så er de lineært uavhengige, derfor kan de tas som grunnlag for rommet R n . La oss finne formen til matrisen til den lineære operatøren A på grunnlag av dens egenvektorer, for hvilke vi handler med operatøren A på basisvektorene: deretter .
Dermed har matrisen til den lineære operatoren A på grunnlag av egenvektorene en diagonal form, og egenverdiene til operatoren A er på diagonalen.
Er det et annet grunnlag der matrisen har en diagonal form? Svaret på dette spørsmålet er gitt av følgende teorem.

Teorem. Matrisen til en lineær operator A i basisen (i = 1..n) har en diagonal form hvis og bare hvis alle vektorene til basisen er egenvektorer til operatoren A.

Regel for å finne egenverdier og egenvektorer

. (*)

(1)
hvor er matrisen til den lineære operatoren.

System (1) har en løsning som ikke er null hvis determinanten D er lik null

Eksempel 12. Den lineære operatoren A virker i R 3 i henhold til loven , hvor x 1 , x 2 , .., x n er koordinatene til vektoren i basisen , , . Finn egenverdiene og egenvektorene til denne operatoren.
Løsning. Vi bygger matrisen til denne operatøren:
.
Vi komponerer et system for å bestemme koordinatene til egenvektorer:

Vi komponerer den karakteristiske ligningen og løser den:

.
λ 1,2 = -1, λ 3 = 3.
Ved å erstatte λ = -1 i systemet, har vi:
eller
Fordi , så er det to avhengige variabler og en fri variabel.
La x 1 være en ledig ukjent, da Vi løser dette systemet på hvilken som helst måte og finner den generelle løsningen til dette systemet: Det grunnleggende løsningssystemet består av én løsning, siden n - r = 3 - 2 = 1.
Settet med egenvektorer som tilsvarer egenverdien λ = -1 har formen: , hvor x 1 er et hvilket som helst annet tall enn null. La oss velge en vektor fra dette settet, for eksempel ved å sette x 1 = 1: .
Ved å argumentere på samme måte finner vi egenvektoren som tilsvarer egenverdien λ = 3: .
I rommet R 3 består basisen av tre lineært uavhengige vektorer, men vi har kun fått to lineært uavhengige egenvektorer, som basisen i R 3 ikke kan dannes fra. Følgelig kan ikke matrisen A til en lineær operator reduseres til en diagonal form.

Eksempel 13 Gitt en matrise .
1. Bevis at vektoren er en egenvektor til matrisen A. Finn egenverdien som tilsvarer denne egenvektoren.
2. Finn et grunnlag der matrisen A har diagonal form.
Løsning.
1. Hvis , så er en egenvektor

.
Vektor (1, 8, -1) er en egenvektor. Egenverdi λ = -1.
Matrisen har en diagonal form i grunnlaget bestående av egenvektorer. En av dem er kjent. La oss finne resten.
Vi ser etter egenvektorer fra systemet:

Karakteristisk ligning: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Finn egenvektoren som tilsvarer egenverdien λ = -3:

Rangeringen av matrisen til dette systemet er lik to og er lik antall ukjente, derfor har dette systemet bare en nullløsning x 1 = x 3 = 0. x 2 her kan være alt annet enn null, for eksempel, x 2 = 1. Dermed er vektoren (0 ,1,0) en egenvektor som tilsvarer λ = -3. La oss sjekke:
.
Hvis λ = 1, får vi systemet
Rangeringen av matrisen er to. Stryk ut den siste ligningen.
La x 3 være den frie ukjente. Deretter x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Forutsatt x 3 = 1, har vi (-3,-9,1) - en egenvektor som tilsvarer egenverdien λ = 1. Sjekk:

.
Siden egenverdiene er reelle og forskjellige, er vektorene som tilsvarer dem lineært uavhengige, så de kan tas som grunnlag i R 3 . Altså i grunnlaget , , matrise A har formen:
.
Ikke hver matrise av en lineær operator A:R n → R n kan reduseres til en diagonal form, siden det for noen lineære operatorer kan være mindre enn n lineært uavhengige egenvektorer. Imidlertid, hvis matrisen er symmetrisk, tilsvarer nøyaktig m lineært uavhengige vektorer roten til den karakteristiske ligningen av multiplisitet m.

Definisjon. En symmetrisk matrise er en kvadratisk matrise der elementene som er symmetriske i forhold til hoveddiagonalen er like, det vil si hvor .
Merknader. 1. Alle egenverdier til en symmetrisk matrise er reelle.
2. Egenvektorer til en symmetrisk matrise som tilsvarer parvis forskjellige egenverdier er ortogonale.
Som en av de mange anvendelsene av det studerte apparatet, vurderer vi problemet med å bestemme formen til en andreordenskurve.