Różnorodność jego typów. Obliczanie wariancji grupowej, międzygrupowej i całkowitej (zgodnie z zasadą dodawania wariancji)
 .
.
I odwrotnie, jeśli jest nieujemnym a.e. funkcjonować tak, że  , to istnieje absolutnie ciągła miara prawdopodobieństwa taka, że jest to jej gęstość.
, to istnieje absolutnie ciągła miara prawdopodobieństwa taka, że jest to jej gęstość.
Zastąpienie miary w całce Lebesgue’a:
 ,
,
gdzie jest dowolną funkcją borelową, która jest całkowalna względem miary prawdopodobieństwa.
Dyspersja, rodzaje i właściwości dyspersji. Pojęcie dyspersji
Rozproszenie w statystyce oblicza się jako odchylenie standardowe poszczególnych wartości cechy do kwadratu od średniej arytmetycznej. W zależności od danych początkowych wyznacza się ją za pomocą prostych i ważonych wzorów na wariancję:
1. Prosta różnica(dla danych niezgrupowanych) oblicza się ze wzoru:
![]()
2. Wariancja ważona (dla serii zmian):

gdzie n to częstotliwość (powtarzalność współczynnika X)
Przykład znajdowania wariancji
Na tej stronie opisano standardowy przykład znajdowania wariancji. Możesz także przyjrzeć się innym problemom związanym ze znalezieniem wariancji
Przykład 1. Wyznaczanie wariancji grupowej, średniej grupowej, międzygrupowej i całkowitej
Przykład 2. Znajdowanie wariancji i współczynnika zmienności w tabeli grupującej
Przykład 3. Znajdowanie wariancji w szeregu dyskretnym
Przykład 4. Poniższe dane są dostępne dla grupy 20 studentów korespondencyjnych. Należy skonstruować szereg przedziałowy rozkładu cechy, obliczyć średnią wartość cechy i zbadać jej rozproszenie

Zbudujmy grupowanie interwałowe. Wyznaczmy zakres przedziału korzystając ze wzoru:
![]()
gdzie X max jest maksymalną wartością cechy grupującej; X min – minimalna wartość cechy grupującej; n – liczba przedziałów:
Przyjmujemy n=5. Krok wynosi: h = (192 - 159)/ 5 = 6,6
Utwórzmy grupowanie interwałowe

Do dalszych obliczeń zbudujemy tabelę pomocniczą:

X"i – środek przedziału. (np. środek przedziału 159 – 165,6 = 162,3)
Średni wzrost uczniów określamy za pomocą wzoru na średnią ważoną arytmetyczną:

Wyznaczmy wariancję korzystając ze wzoru:
Formułę można przekształcić w następujący sposób:

Z tego wzoru wynika, że wariancja jest równa różnica między średnią kwadratów opcji a kwadratem i średnią.
Dyspersja w szeregach wariacyjnych o równych odstępach metodą momentów można obliczyć w następujący sposób, korzystając z drugiej właściwości dyspersji (dzielenie wszystkich opcji przez wartość przedziału). Określanie wariancji, obliczony metodą momentów, zastosowanie poniższego wzoru jest mniej pracochłonne:

gdzie i jest wartością przedziału; A jest konwencjonalnym zerem, dla którego wygodnie jest użyć środka przedziału o najwyższej częstotliwości; m1 jest kwadratem momentu pierwszego rzędu; m2 - moment drugiego rzędu
Alternatywna wariancja cechy (jeżeli w populacji statystycznej cecha zmienia się w taki sposób, że istnieją tylko dwie wzajemnie wykluczające się możliwości, to taką zmienność nazywamy alternatywną) można obliczyć korzystając ze wzoru:

Podstawiając q = 1- p do tego wzoru na dyspersję, otrzymujemy:

Rodzaje wariancji
Całkowita rozbieżność mierzy zmienność cechy w całej populacji jako całości pod wpływem wszystkich czynników powodujących tę zmienność. Jest równy średniemu kwadratowi odchyleń poszczególnych wartości cechy x od ogólnej średniej wartości x i można go zdefiniować jako wariancję prostą lub wariancję ważoną.
Wariancja wewnątrzgrupowa charakteryzuje się zmiennością losową, tj. część zmienności, która wynika z wpływu nieuwzględnionych czynników i nie zależy od atrybutu czynnika, który stanowi podstawę grupy. Rozrzut taki jest równy średniemu kwadratowi odchyleń poszczególnych wartości atrybutu w obrębie grupy X od średniej arytmetycznej grupy i można go obliczyć jako rozproszenie proste lub rozproszenie ważone.
Zatem, miary wariancji wewnątrzgrupowej zmienność cechy w obrębie grupy i określa się ją według wzoru:

gdzie xi jest średnią grupy; ni to liczba jednostek w grupie.
Na przykład wariancje wewnątrzgrupowe, które należy określić w zadaniu badania wpływu kwalifikacji pracowników na poziom wydajności pracy w warsztacie, pokazują zróżnicowanie wydajności w każdej grupie spowodowane wszystkimi możliwymi czynnikami (stan techniczny sprzętu, dostępność narzędzia i materiały, wiek pracowników, pracochłonność itp.), z wyjątkiem różnic w kategorii kwalifikacji (w obrębie grupy wszyscy pracownicy mają takie same kwalifikacje).
Średnia wariancji wewnątrzgrupowych odzwierciedla wariancję losową, czyli tę część wariancji, która wystąpiła pod wpływem wszystkich pozostałych czynników, z wyjątkiem czynnika grupującego. Oblicza się go za pomocą wzoru:

Wariancja międzygrupowa charakteryzuje systematyczną zmienność wynikowej cechy, która wynika z wpływu czynnika-atrybutu, który stanowi podstawę grupy. Jest równy średniemu kwadratowi odchyleń średnich grupowych od średniej ogólnej. Wariancję międzygrupową oblicza się za pomocą wzoru:

Oczekiwanie i wariancja to najczęściej używane cechy liczbowe zmiennej losowej. Charakteryzują najważniejsze cechy rozkładu: jego położenie i stopień rozproszenia. W wielu praktycznych problemach pełna, wyczerpująca charakterystyka zmiennej losowej – prawo dystrybucji – albo w ogóle nie może zostać uzyskana, albo w ogóle nie jest potrzebna. W takich przypadkach ogranicza się do przybliżonego opisu zmiennej losowej za pomocą charakterystyk numerycznych.
Wartość oczekiwana jest często nazywana po prostu średnią wartością zmiennej losowej. Rozproszenie zmiennej losowej jest cechą dyspersji, rozproszenia zmiennej losowej wokół jej oczekiwań matematycznych.
Oczekiwanie dyskretnej zmiennej losowej
Przyjrzyjmy się koncepcji oczekiwań matematycznych, opierając się najpierw na mechanicznej interpretacji rozkładu dyskretnej zmiennej losowej. Niech masa jednostkowa zostanie rozłożona pomiędzy punktami osi x X1 , X 2 , ..., X N, a każdemu punktowi materialnemu odpowiada masa P1 , P 2 , ..., P N. Należy wybrać jeden punkt na osi odciętych, charakteryzujący położenie całego układu punktów materialnych, z uwzględnieniem ich mas. Naturalnym jest, że za taki punkt przyjmuje się środek masy układu punktów materialnych. Jest to średnia ważona zmiennej losowej X, do której odcięta jest każdy punkt XI wchodzi z „wagą” równą odpowiedniemu prawdopodobieństwu. Uzyskana w ten sposób średnia wartość zmiennej losowej X nazywa się jego oczekiwaniem matematycznym.
Matematyczne oczekiwanie dyskretnej zmiennej losowej jest sumą iloczynów wszystkich jej możliwych wartości i prawdopodobieństw tych wartości:

Przykład 1. Zorganizowano loterię, w której wygrywają obie strony. Wygranych jest 1000, z czego 400 to 10 rubli. 300 - 20 rubli za sztukę. 200 - 100 rubli za sztukę. i 100 - 200 rubli za sztukę. Jaka jest średnia wygrana osoby, która kupi jeden los?
Rozwiązanie. Średnie wygrane znajdziemy, jeśli podzielimy całkowitą kwotę wygranych, która wynosi 10*400 + 20*300 + 100*200 + 200*100 = 50 000 rubli, przez 1000 (całkowita kwota wygranych). Następnie otrzymujemy 50000/1000 = 50 rubli. Jednak wyrażenie służące do obliczenia średnich wygranych można przedstawić w następującej formie:

Z drugiej strony w tych warunkach zwycięska wielkość jest zmienną losową, która może przyjmować wartości 10, 20, 100 i 200 rubli. z prawdopodobieństwem równym odpowiednio 0,4; 0,3; 0,2; 0,1. Dlatego oczekiwana średnia wygrana jest równa sumie iloczynów wielkości wygranych i prawdopodobieństwa ich otrzymania.
Przykład 2. Wydawca podjął decyzję o wydaniu nowej książki. Planuje sprzedać książkę za 280 rubli, z czego sam otrzyma 200, 50 – księgarnia i 30 – autor. Tabela zawiera informacje o kosztach wydania książki i prawdopodobieństwie sprzedaży określonej liczby egzemplarzy książki.
Znajdź oczekiwany zysk wydawcy.
Rozwiązanie. Zmienna losowa „zysk” jest równa różnicy między przychodem ze sprzedaży a kosztem wydatków. Na przykład, jeśli sprzedanych zostanie 500 egzemplarzy książki, dochód ze sprzedaży wyniesie 200 * 500 = 100 000, a koszt publikacji to 225 000 rubli. Tym samym wydawcy grozi strata w wysokości 125 000 rubli. Poniższa tabela podsumowuje oczekiwane wartości zmiennej losowej – zysk:
| Numer | Zysk XI | Prawdopodobieństwo PI | XI P I |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Całkowity: | 1,00 | 25000 |
Otrzymujemy w ten sposób matematyczne oczekiwanie zysku wydawcy:
![]() .
.
Przykład 3. Prawdopodobieństwo trafienia jednym strzałem P= 0,2. Określ zużycie pocisków, które zapewniają matematyczną oczekiwaną liczbę trafień równą 5.
Rozwiązanie. Z tego samego matematycznego wzoru oczekiwań, którego używaliśmy do tej pory, wyrażamy X- zużycie powłoki:
![]() .
.
Przykład 4. Określ oczekiwanie matematyczne zmiennej losowej X liczba trafień trzema strzałami, jeżeli prawdopodobieństwo trafienia przy każdym strzale P = 0,4 .
Wskazówka: znajdź prawdopodobieństwo wartości zmiennych losowych według Wzór Bernoulliego .
Właściwości oczekiwań matematycznych
Rozważmy właściwości oczekiwań matematycznych.
Właściwość 1. Matematyczne oczekiwanie na stałą wartość jest równe tej stałej:
Własność 2. Stały współczynnik można wyjąć z matematycznego znaku oczekiwania:
![]()
Własność 3. Oczekiwanie matematyczne sumy (różnicy) zmiennych losowych jest równe sumie (różnicy) ich oczekiwań matematycznych:
Właściwość 4. Oczekiwanie matematyczne iloczynu zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych:
Własność 5. Jeśli wszystkie wartości zmiennej losowej X zmniejszyć (zwiększyć) o tę samą liczbę Z, to jego oczekiwanie matematyczne zmniejszy się (zwiększy) o tę samą liczbę:
![]()
Kiedy nie możesz ograniczyć się tylko do oczekiwań matematycznych
W większości przypadków jedynie oczekiwanie matematyczne nie jest w stanie w wystarczającym stopniu scharakteryzować zmiennej losowej.
Niech zmienne losowe X I Y wynikają z następujących praw dystrybucji:
| Oznaczający X | Prawdopodobieństwo |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Oznaczający Y | Prawdopodobieństwo |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Oczekiwania matematyczne tych wielkości są takie same – równe zeru:


Jednak ich schematy dystrybucji są różne. Losowa wartość X może przyjmować jedynie wartości niewiele różniące się od oczekiwań matematycznych oraz zmienną losową Y może przyjmować wartości znacznie odbiegające od oczekiwań matematycznych. Podobny przykład: średnia płaca nie pozwala ocenić udziału wysoko i nisko opłacanych pracowników. Innymi słowy, na podstawie oczekiwań matematycznych nie można ocenić, jakie odchylenia od nich, przynajmniej średnio, są możliwe. Aby to zrobić, musisz znaleźć wariancję zmiennej losowej.
Wariancja dyskretnej zmiennej losowej
Zmienność Dyskretna zmienna losowa X nazywa się oczekiwaniem matematycznym kwadratu jego odchylenia od oczekiwania matematycznego:

Odchylenie standardowe zmiennej losowej X wartość arytmetyczną pierwiastka kwadratowego z jej wariancji nazywa się:
![]() .
.
Przykład 5. Obliczanie wariancji i odchyleń standardowych zmiennych losowych X I Y, których prawa dystrybucji podano w tabelach powyżej.
Rozwiązanie. Matematyczne oczekiwania zmiennych losowych X I Y, jak stwierdzono powyżej, są równe zeru. Zgodnie ze wzorem dyspersji przy mi(X)=mi(y)=0 otrzymujemy:


Następnie odchylenia standardowe zmiennych losowych X I Y makijaż
![]() .
.
Zatem przy tych samych oczekiwaniach matematycznych wariancja zmiennej losowej X bardzo mała, ale zmienna losowa Y- istotne. Jest to konsekwencja różnic w ich rozmieszczeniu.
Przykład 6. Inwestor posiada 4 alternatywne projekty inwestycyjne. Tabela podsumowuje oczekiwany zysk w tych projektach z odpowiednim prawdopodobieństwem.
| Projekt 1 | Projekt 2 | Projekt 3 | Projekt 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Znajdź matematyczne oczekiwanie, wariancję i odchylenie standardowe dla każdej alternatywy.
Rozwiązanie. Pokażmy, jak obliczane są te wartości dla 3. alternatywy:
Tabela podsumowuje znalezione wartości dla wszystkich alternatyw.
Wszystkie alternatywy mają te same oczekiwania matematyczne. Oznacza to, że w dłuższej perspektywie wszyscy mają takie same dochody. Odchylenie standardowe można interpretować jako miarę ryzyka – im jest ono wyższe, tym większe ryzyko inwestycji. Inwestor, który nie chce dużego ryzyka, wybierze projekt 1, ponieważ ma najmniejsze odchylenie standardowe (0). Jeżeli inwestor preferuje ryzyko i wysokie zyski w krótkim czasie, to wybierze projekt o największym odchyleniu standardowym – projekt 4.
Właściwości dyspersyjne
Przedstawmy właściwości dyspersji.
Właściwość 1. Wariancja stałej wartości wynosi zero:
Własność 2. Stały współczynnik można usunąć ze znaku dyspersji podnosząc go do kwadratu:
![]() .
.
Własność 3. Wariancja zmiennej losowej jest równa matematycznemu oczekiwaniu kwadratu tej wartości, od którego odejmuje się kwadrat matematycznego oczekiwania samej wartości:
![]() ,
,
Gdzie ![]() .
.
Właściwość 4. Wariancja sumy (różnicy) zmiennych losowych jest równa sumie (różnicy) ich wariancji:
Przykład 7. Wiadomo, że dyskretna zmienna losowa X przyjmuje tylko dwie wartości: −3 i 7. Ponadto znane jest oczekiwanie matematyczne: mi(X) = 4 . Znajdź wariancję dyskretnej zmiennej losowej.
Rozwiązanie. Oznaczmy przez P prawdopodobieństwo, z jakim zmienna losowa przyjmuje wartość X1 = −3 . Następnie prawdopodobieństwo wartości X2 = 7 będzie 1- P. Wyprowadźmy równanie na oczekiwanie matematyczne:
mi(X) = X 1 P + X 2 (1 − P) = −3P + 7(1 − P) = 4 ,
gdzie otrzymujemy prawdopodobieństwa: P= 0,3 i 1 − P = 0,7 .
Prawo rozkładu zmiennej losowej:
| X | −3 | 7 |
| P | 0,3 | 0,7 |
Wariancję tej zmiennej losowej obliczamy korzystając ze wzoru z właściwości 3 dyspersji:
D(X) = 2,7 + 34,3 − 16 = 21 .
Znajdź samodzielnie matematyczne oczekiwanie zmiennej losowej, a następnie spójrz na rozwiązanie
Przykład 8. Dyskretna zmienna losowa X przyjmuje tylko dwie wartości. Przyjmuje większą z wartości 3 z prawdopodobieństwem 0,4. Ponadto znana jest wariancja zmiennej losowej D(X) = 6 . Znajdź matematyczne oczekiwanie zmiennej losowej.
Przykład 9. W urnie jest 6 kul białych i 4 czarne. Z urny losujemy 3 kule. Liczba białych kul wśród wylosowanych kul jest dyskretną zmienną losową X. Znajdź matematyczne oczekiwanie i wariancję tej zmiennej losowej.
Rozwiązanie. Losowa wartość X może przyjmować wartości 0, 1, 2, 3. Z odpowiednich prawdopodobieństw można obliczyć reguła mnożenia prawdopodobieństwa. Prawo rozkładu zmiennej losowej:
| X | 0 | 1 | 2 | 3 |
| P | 1/30 | 3/10 | 1/2 | 1/6 |
Stąd matematyczne oczekiwanie tej zmiennej losowej:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
Wariancja danej zmiennej losowej wynosi:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Oczekiwanie i wariancja ciągłej zmiennej losowej
W przypadku ciągłej zmiennej losowej mechaniczna interpretacja oczekiwań matematycznych zachowa to samo znaczenie: środek masy jednostki masy rozłożonej w sposób ciągły na osi x z gęstością F(X). W przeciwieństwie do dyskretnej zmiennej losowej, której argumentem jest funkcja XI zmienia się gwałtownie; w przypadku ciągłej zmiennej losowej argument zmienia się w sposób ciągły. Ale matematyczne oczekiwanie ciągłej zmiennej losowej jest również powiązane z jej średnią wartością.
Aby znaleźć matematyczne oczekiwanie i wariancję ciągłej zmiennej losowej, należy znaleźć całki oznaczone . Jeśli podana jest funkcja gęstości ciągłej zmiennej losowej, to wchodzi ona bezpośrednio do całki. Jeśli podana jest funkcja rozkładu prawdopodobieństwa, to różniczkując ją, musisz znaleźć funkcję gęstości.
Nazywa się ją średnią arytmetyczną wszystkich możliwych wartości ciągłej zmiennej losowej oczekiwanie matematyczne, oznaczone lub .
ObliczmySMPRZEWYŻSZAĆwariancja próbki i odchylenie standardowe. Obliczymy także wariancję zmiennej losowej, jeśli znany jest jej rozkład.
Najpierw rozważmy dyspersja, Następnie odchylenie standardowe.
Odchylenie próbki
Odchylenie próbki (wariancja próbki,próbkazmienność) charakteryzuje rozrzut wartości w tablicy względem .
Wszystkie 3 wzory są matematycznie równoważne.
Z pierwszego wzoru wynika, że wariancja próbki jest sumą kwadratów odchyleń każdej wartości w tablicy od średniej podzielone przez wielkość próby minus 1.
odchylenia próbki używana jest funkcja DISP(), angielski. nazwa VAR, tj. Zmienność. Od wersji MS EXCEL 2010 zaleca się stosowanie jej analogu DISP.V(), w języku angielskim. nazwa VARS, tj. Przykładowa zmienność. Dodatkowo począwszy od wersji MS EXCEL 2010 dostępna jest funkcja DISP.Г(), w języku angielskim. nazwa VARP, tj. Wariancja populacji, która oblicza dyspersja Dla populacja. Cała różnica sprowadza się do mianownika: zamiast n-1, jak DISP.V(), DISP.G() ma w mianowniku tylko n. Przed wersją MS EXCEL 2010 do obliczania wariancji populacji używano funkcji VAR().
Odchylenie próbki
=QUADROTCL(Próbka)/(LICZBA(Próbka)-1)
=(SUMA(Próbka)-LICZBA(Próbka)*ŚREDNIA(Próbka)^2)/ (LICZBA(Próbka)-1)– zwykła formuła
=SUMA((Próbka -ŚREDNIA(Próbka))^2)/ (LICZBA(Próbka)-1) –
Odchylenie próbki jest równy 0, tylko wtedy, gdy wszystkie wartości są sobie równe i odpowiednio równe Średnia wartość. Zwykle im większa wartość odchylenia, tym większy jest rozrzut wartości w tablicy.
Odchylenie próbki jest oceną punktową odchylenia rozkład zmiennej losowej, z której został utworzony próbka. O budowie przedziały ufności podczas oceniania odchylenia można przeczytać w artykule.
Wariancja zmiennej losowej
Liczyć dyspersja zmienna losowa, musisz ją znać.
Dla odchylenia zmienna losowa X jest często oznaczana jako Var(X). Dyspersja równy kwadratowi odchylenia od średniej E(X): Var(X)=E[(X-E(X)) 2 ]
dyspersja obliczane według wzoru:

gdzie x i to wartość, jaką może przyjąć zmienna losowa, a μ to wartość średnia (), p(x) to prawdopodobieństwo, że zmienna losowa przyjmie wartość x.
Jeśli zmienna losowa ma , to dyspersja obliczane według wzoru:

Wymiar odchylenia odpowiada kwadratowi jednostki miary wartości pierwotnych. Na przykład, jeśli wartości w próbce reprezentują pomiary masy części (w kg), wówczas wymiarem wariancji będzie kg 2 . Może to być trudne do zinterpretowania, aby scharakteryzować rozrzut wartości, wartość równą pierwiastkowi kwadratowemu odchylenia – odchylenie standardowe.
Niektóre właściwości odchylenia:
Var(X+a)=Var(X), gdzie X jest zmienną losową, a a jest stałą.
Var(aХ)=a 2 Var(X)
Var(X)=E[(X-E(X)) 2 ]=E=E(X 2)-E(2*X*E(X))+(E(X)) 2 =E(X 2)- 2*E(X)*E(X)+(E(X)) 2 =E(X 2)-(E(X)) 2
Ta właściwość dyspersji jest wykorzystywana w artykuł o regresji liniowej.
Var(X+Y)=Var(X) + Var(Y) + 2*Cov(X;Y), gdzie X i Y to zmienne losowe, Cov(X;Y) to kowariancja tych zmiennych losowych.
Jeśli zmienne losowe są niezależne, to tak kowariancja jest równe 0, a zatem Var(X+Y)=Var(X)+Var(Y). Ta właściwość dyspersji jest wykorzystywana w wyprowadzaniu.
Pokażmy, że dla wielkości niezależnych Var(X-Y)=Var(X+Y). Rzeczywiście, Var(X-Y)= Var(X-Y)= Var(X+(-Y))= Var(X)+Var(-Y)= Var(X)+Var(-Y)= Var( X)+(- 1) 2 Var(Y)= Var(X)+Var(Y)= Var(X+Y). Ta właściwość dyspersji jest używana do konstruowania .
Odchylenie standardowe próbki
Odchylenie standardowe próbki jest miarą tego, jak bardzo rozproszone są wartości w próbce w stosunku do ich wartości.
A-przeorat, odchylenie standardowe równy pierwiastkowi kwadratowemu z odchylenia:

Odchylenie standardowe nie bierze pod uwagę wielkości wartości w próbka, a jedynie stopień rozproszenia wartości wokół nich przeciętny. Aby to zilustrować, podamy przykład.
Obliczmy odchylenie standardowe dla 2 próbek: (1; 5; 9) i (1001; 1005; 1009). W obu przypadkach s=4. Oczywiste jest, że stosunek odchylenia standardowego do wartości tablicy różni się znacznie pomiędzy próbkami. W takich przypadkach się go stosuje Współczynnik zmienności(Współczynnik zmienności, CV) - stosunek Odchylenie standardowe do średniej arytmetyka, wyrażona w procentach.
W MS EXCEL 2007 i wcześniejszych wersjach do obliczeń Odchylenie standardowe próbki używana jest funkcja =STDEVAL(), angielski. nazwa STDEV, tj. Odchylenie standardowe. Od wersji MS EXCEL 2010 zaleca się stosowanie jego odpowiednika =STDEV.B() , angielskiego. nazwa STDEV.S, tj. Odchylenie standardowe próbki.
Dodatkowo począwszy od wersji MS EXCEL 2010 dostępna jest funkcja STANDARDEV.G(), angielska. nazwa STDEV.P, tj. Odchylenie standardowe populacji, które oblicza odchylenie standardowe Dla populacja. Cała różnica sprowadza się do mianownika: zamiast n-1 jak w STANDARDEV.V(), STANDARDEVAL.G() ma w mianowniku tylko n.
Odchylenie standardowe można również obliczyć bezpośrednio za pomocą poniższych wzorów (patrz przykładowy plik)
=ROOT(QUADROTCL(próbka)/(LICZBA(próbka)-1))
=ROOT((SUMA(Próbka)-LICZ(Próbka)*ŚREDNIA(Próbka)^2)/(LICZBA(Próbka)-1))
Inne miary rozproszenia
Funkcja SQUADROTCL() wykonuje obliczenia za pomocą suma kwadratów odchyleń wartości od ich przeciętny. Ta funkcja zwróci taki sam wynik jak formuła =DISP.G( Próbka)*SPRAWDZAĆ( Próbka) , Gdzie Próbka- odwołanie do zakresu zawierającego tablicę przykładowych wartości (). Obliczenia w funkcji QUADROCL() wykonujemy według wzoru:

Funkcja SROTCL() jest także miarą rozproszenia zbioru danych. Funkcja SROTCL() oblicza średnią z wartości bezwzględnych odchyleń wartości od przeciętny. Ta funkcja zwróci taki sam wynik jak formuła =SUMAPRODUKT(ABS(Próbka-ŚREDNIA(Próbka)))/LICZBA(Próbka), Gdzie Próbka- link do zakresu zawierającego tablicę przykładowych wartości.
Obliczenia w funkcji SROTCL() wykonujemy według wzoru:

Gdzie σ 2 j jest wariancją wewnątrzgrupową j-tej grupy.
Dla niezgrupowanych danych wariancja resztkowa– miara dokładności aproksymacji, tj. przybliżenie linii regresji do danych oryginalnych: 
gdzie y(t) – prognoza według równania trendu; y t – szereg dynamiki początkowej; n – liczba punktów; p – liczba współczynników równania regresji (liczba zmiennych objaśniających).
W tym przykładzie jest to tzw nieobciążony estymator wariancji.
Przykład nr 1. Podział pracowników trzech przedsiębiorstw jednego stowarzyszenia według kategorii taryfowych charakteryzuje się następującymi danymi:
| Kategoria taryfowa pracownika | Liczba pracowników w przedsiębiorstwie | ||
| przedsiębiorstwo 1 | przedsiębiorstwo 2 | przedsiębiorstwo 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
Definiować:
1. wariancja dla każdego przedsiębiorstwa (wariancje wewnątrzgrupowe);
2. średnia wariancji wewnątrzgrupowych;
3. rozproszenie międzygrupowe;
4. wariancja całkowita.
Rozwiązanie.
Przed przystąpieniem do rozwiązywania problemu należy dowiedzieć się, która cecha jest skuteczna, a która silniowa. W rozpatrywanym przykładzie atrybutem wynikowym jest „Kategoria taryfowa”, a atrybutem czynnikowym „Numer (nazwa) przedsiębiorstwa”.
Mamy wtedy trzy grupy (przedsiębiorstwa), dla których należy obliczyć średnią grupową i wariancje wewnątrzgrupowe:

| Firma | średnia grupy, | wariancja wewnątrzgrupowa, |
| 1 | 4 | 1,8 |
Średnia wariancji wewnątrzgrupowych ( wariancja resztkowa) zostanie obliczona według wzoru:
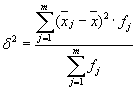
gdzie możesz obliczyć:

Lub:

Następnie:
Całkowita wariancja będzie równa: s 2 = 1,6 + 0 = 1,6.
Całkowitą wariancję można również obliczyć za pomocą jednego z dwóch poniższych wzorów:
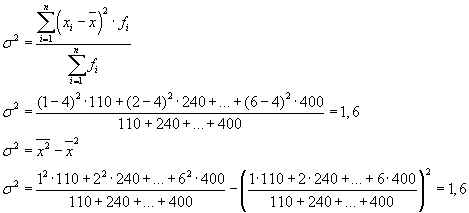
Rozwiązując problemy praktyczne, często mamy do czynienia z cechą, która przyjmuje tylko dwie alternatywne wartości. W tym przypadku nie mówimy o wadze określonej wartości cechy, ale o jej udziale w całości. Jeżeli odsetek jednostek populacji posiadających badaną cechę oznaczymy jako „ R", a ci, którzy nie mają - przez " Q", wówczas wariancję można obliczyć korzystając ze wzoru:
s2 = p×q
Przykład nr 2. Na podstawie danych produkcyjnych sześciu pracowników w zespole określ wariancję międzygrupową i oceń wpływ zmiany roboczej na ich wydajność pracy, jeśli całkowita wariancja wynosi 12,2.
| Pracownik zespołu nr. | Wydajność pracownika, szt. | |
| na pierwszej zmianie | na drugiej zmianie | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
Rozwiązanie. Wstępne dane
| X | f 1 | f 2 | f 3 | f 4 | f 5 | f 6 | Całkowity |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| Całkowity | 31 | 33 | 37 | 37 | 40 | 38 |
Mamy wówczas 6 grup, dla których należy obliczyć średnią grupową i wariancje wewnątrzgrupowe.
1. Znajdź średnie wartości każdej grupy.
2. Znajdź średni kwadrat każdej grupy.
Podsumujmy wyniki obliczeń w tabeli:
| Numer grupy | Średnia grupy | Wariancja wewnątrzgrupowa |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. Wariancja wewnątrzgrupowa charakteryzuje zmianę (odmianę) badanej (wynikowej) cechy w obrębie grupy pod wpływem wszystkich czynników na nią wpływających, z wyjątkiem czynnika leżącego u podstaw grupowania:
Średnią wariancji wewnątrzgrupowych obliczymy ze wzoru:
4. Wariancja międzygrupowa charakteryzuje zmianę (odmianę) badanej (wynikowej) cechy pod wpływem czynnika (cechy czynnikowej), który stanowi podstawę grupy.
Wariancję międzygrupową definiujemy jako:
Gdzie
Następnie
Całkowita rozbieżność charakteryzuje zmianę (odmianę) badanej (wynikowej) cechy pod wpływem wszystkich czynników (charakterystyk czynnikowych) bez wyjątku. Zgodnie z warunkami zadania jest on równy 12,2.
Empiryczna zależność korelacyjna mierzy, jaka część całkowitej zmienności wynikowej cechy jest spowodowana przez badany czynnik. Jest to stosunek wariancji czynnika do wariancji całkowitej:
Definiujemy empiryczną relację korelacji:
Powiązania między cechami mogą być słabe i mocne (bliskie). Ich kryteria oceniane są w skali Chaddocka:
0,1 0,3 0,5 0,7 0,9 W naszym przykładzie związek pomiędzy cechą Y i czynnikiem X jest słaby
Współczynnik determinacji.
Wyznaczmy współczynnik determinacji:
Zatem 0,67% zmienności wynika z różnic między cechami, a 99,37% z innych czynników.
Wniosek: w tym przypadku wydajność pracowników nie jest uzależniona od pracy na określonej zmianie, tj. wpływ zmiany pracy na ich wydajność pracy jest niewielki i wynika z innych czynników.
Przykład nr 3. Na podstawie danych o przeciętnym wynagrodzeniu i kwadratach odchyleń od jego wartości dla dwóch grup pracowników znajdź wariancję całkowitą, stosując zasadę dodawania wariancji:
Rozwiązanie:Średnia wariancji wewnątrzgrupowych
Wariancję międzygrupową definiujemy jako:
Całkowita wariancja będzie wynosić: 480 + 13824 = 14304
Często w statystyce, analizując zjawisko lub proces, konieczne jest uwzględnienie nie tylko informacji o średnich poziomach badanych wskaźników, ale także rozproszenie lub zmienność wartości poszczególnych jednostek , co jest ważną cechą badanej populacji.
Najbardziej podlegającym wahaniom są ceny akcji, podaż i popyt oraz stopy procentowe w różnych okresach i w różnych miejscach.
Główne wskaźniki charakteryzujące zmienność , to zakres, rozproszenie, odchylenie standardowe i współczynnik zmienności.
Zakres zmienności reprezentuje różnicę między wartościami maksymalnymi i minimalnymi cechy: R = Xmax – Xmin. Wadą tego wskaźnika jest to, że ocenia on jedynie granice zmienności cechy i nie odzwierciedla jej zmienności w tych granicach.
Dyspersja brakuje tego mankamentu. Oblicza się go jako średni kwadrat odchyleń wartości charakterystycznych od ich wartości średniej:
Uproszczony sposób obliczania wariancji przeprowadza się za pomocą następujących wzorów (prostych i ważonych):
Przykłady zastosowania tych wzorów przedstawiono w zadaniach 1 i 2.
Powszechnie stosowanym w praktyce wskaźnikiem jest odchylenie standardowe :
Odchylenie standardowe definiuje się jako pierwiastek kwadratowy wariancji i ma ten sam wymiar co badana cecha.
Uwzględnione wskaźniki pozwalają uzyskać wartość bezwzględną zmienności, tj. ocenić ją w jednostkach miary badanej cechy. W przeciwieństwie do nich, współczynnik zmienności mierzy zmienność w ujęciu względnym – w stosunku do średniego poziomu, co w wielu przypadkach jest preferowane.
Wzór na obliczenie współczynnika zmienności.
Przykłady rozwiązywania problemów na temat „Wskaźniki zmienności statystyk”
Problem 1 . Badając wpływ reklamy na wielkość przeciętnej miesięcznej lokaty w bankach w regionie, zbadano 2 banki. Następujące wyniki zostały osiągnięte:
Definiować:
1) dla każdego banku: a) średni miesięczny depozyt; b) rozproszenie składek;
2) przeciętny miesięczny depozyt dla dwóch banków łącznie;
3) Różnica depozytów dla 2 banków, w zależności od reklamy;
4) Różnica depozytów dla 2 banków, w zależności od wszystkich czynników z wyjątkiem reklamy;
5) Całkowita wariancja za pomocą reguły dodawania;
6) Współczynnik determinacji;
7) Relacja korelacyjna.
Rozwiązanie
1) Stwórzmy tabelę kalkulacyjną dla banku z reklamą . Aby wyznaczyć średni miesięczny depozyt, znajdziemy punkty środkowe przedziałów. W tym przypadku wartość otwartego przedziału (pierwszego) jest warunkowo przyrównywana do wartości sąsiadującego z nim przedziału (drugiego).
Średnią wielkość depozytu wyznaczymy korzystając ze wzoru na średnią ważoną arytmetyczną:
29 000/50 = 580 rubli.
Wariancję wkładu wyznaczamy za pomocą wzoru:
23 400/50 = 468
Będziemy wykonywać podobne działania dla banku bez reklamy :
2) Znajdźmy razem średnią wielkość depozytu dla obu banków. Хср =(580×50+542,8×50)/100 = 561,4 rub.
3) Wariancję lokaty dla dwóch banków w zależności od reklamy wyznaczymy, korzystając ze wzoru: σ 2 =pq (wzór na wariancję alternatywnego atrybutu). Tutaj p=0,5 jest proporcją czynników zależnych od reklamy; q=1-0,5, wówczas σ2 =0,5*0,5=0,25.
4) Ponieważ udział pozostałych czynników wynosi 0,5, to wariancja depozytu dla dwóch banków, w zależności od wszystkich czynników oprócz reklamy, również wynosi 0,25.
5) Wyznacz całkowitą wariancję, korzystając z reguły dodawania.
= (468*50+636,16*50)/100=552,08
= [(580-561,4)250+(542,8-561,4)250] / 100= 34 596/ 100=345,96
σ 2 = σ 2 fakt + σ 2 reszta = 552,08+345,96 = 898,04
6) Współczynnik determinacji η 2 = σ 2 fakt / σ 2 = 345,96/898,04 = 0,39 = 39% - wielkość wkładu w 39% uzależniona jest od reklamy.
7) Empiryczny współczynnik korelacji η = √η 2 = √0,39 = 0,62 – zależność jest dość bliska.
Problem 2 . Istnieje podział przedsiębiorstw według wielkości produktów rynkowych:
Ustalić: 1) rozproszenie wartości produktów rynkowych; 2) odchylenie standardowe; 3) współczynnik zmienności.
Rozwiązanie
1) Według warunku prezentowana jest seria rozkładów przedziałowych. Należy to wyrazić dyskretnie, czyli znaleźć środek przedziału (x"). W grupach przedziałów domkniętych środek znajdujemy za pomocą prostej średniej arytmetycznej. W grupach z górną granicą - jako różnica między tą górną granicą i połowę rozmiaru następnego przedziału (200-(400 -200):2=100).
W grupach z dolną granicą - suma tej dolnej granicy i połowy wielkości poprzedniego przedziału (800+(800-600):2=900).
Średnią wartość produktów rynkowych obliczamy korzystając ze wzoru:
Хср = k×((Σ((x"-a):k)×f):Σf)+a. Tutaj a=500 to wielkość opcji przy najwyższej częstotliwości, k=600-400=200 to wielkość przedziału przy największej częstotliwości Wynik umieśćmy w tabeli:
Zatem średnia wartość produkcji handlowej w badanym okresie wynosi na ogół Хср = (-5:37)×200+500=472,97 tys. rubli.
2) Wariancję znajdujemy za pomocą następującego wzoru:
σ 2 = (33/37)*2002-(472,97-500)2 = 35675,67-730,62 = 34945,05
3) odchylenie standardowe: σ = ±√σ 2 = ±√34945,05 ≈ ±186,94 tysięcy rubli.
4) współczynnik zmienności: V = (σ /Хср)*100 = (186,94 / 472,97)*100 = 39,52%
