Maghanap ng mga eigenvalues at eigenvector ng mga halimbawa ng matrix. Equation ng katangian ng matrix
SISTEMA NG HOMOGENEOUS LINEAR EQUATIONS
Ang isang sistema ng homogenous linear equation ay isang sistema ng anyo
Ito ay malinaw na sa kasong ito ![]() , dahil lahat ng elemento ng isa sa mga column sa mga determinant na ito ay katumbas ng zero.
, dahil lahat ng elemento ng isa sa mga column sa mga determinant na ito ay katumbas ng zero.
Dahil ang mga hindi alam ay matatagpuan sa pamamagitan ng mga formula ![]() , pagkatapos ay sa kaso kapag Δ ≠ 0, ang sistema ay may natatanging zero na solusyon x = y = z= 0. Gayunpaman, sa maraming mga problema ang tanong kung ang isang homogenous na sistema ay may mga solusyon maliban sa zero ay interesado.
, pagkatapos ay sa kaso kapag Δ ≠ 0, ang sistema ay may natatanging zero na solusyon x = y = z= 0. Gayunpaman, sa maraming mga problema ang tanong kung ang isang homogenous na sistema ay may mga solusyon maliban sa zero ay interesado.
Teorama. Para sa isang sistema ng linear homogeneous equation na magkaroon ng nonzero na solusyon, kinakailangan at sapat na Δ ≠ 0.
Kaya, kung ang determinant ay Δ ≠ 0, kung gayon ang sistema ay may natatanging solusyon. Kung Δ ≠ 0, kung gayon ang sistema ng linear homogenous na equation ay may walang katapusang bilang ng mga solusyon.
Mga halimbawa.

Eigenvectors at Matrix Eigenvalues
Hayaang magbigay ng square matrix  , X ay ilang matrix-column na ang taas ay tumutugma sa pagkakasunud-sunod ng matrix A. .
, X ay ilang matrix-column na ang taas ay tumutugma sa pagkakasunud-sunod ng matrix A. .
Sa maraming problema, kailangang isaalang-alang ang equation para sa X
kung saan ang λ ay ilang numero. Ito ay malinaw na para sa anumang λ ang equation na ito ay may zero na solusyon.
Ang bilang na λ kung saan ang equation na ito ay may mga nonzero na solusyon ay tinatawag eigenvalue matrice A, A X para sa gayong λ ay tinatawag sariling vector matrice A.
Hanapin natin ang eigenvector ng matrix A. Dahil ang E∙X=X, kung gayon ang matrix equation ay maaaring muling isulat bilang ![]() o
o ![]() . Sa pinalawak na anyo, ang equation na ito ay maaaring muling isulat bilang isang sistema ng mga linear na equation. Talaga
. Sa pinalawak na anyo, ang equation na ito ay maaaring muling isulat bilang isang sistema ng mga linear na equation. Talaga  .
.
At samakatuwid 
Kaya, nakakuha kami ng isang sistema ng homogenous linear equation para sa pagtukoy ng mga coordinate x 1, x2, x 3 vector X. Para sa system na magkaroon ng mga non-zero na solusyon, kinakailangan at sapat na ang determinant ng system ay katumbas ng zero, i.e.

Ito ay isang 3rd degree na equation na may kinalaman sa λ. Ang tawag dito katangian equation matrice A at nagsisilbi upang matukoy ang mga eigenvalues λ.
Ang bawat eigenvalue λ ay tumutugma sa isang eigenvector X, na ang mga coordinate ay tinutukoy mula sa system sa katumbas na halaga ng λ.
Mga halimbawa.
VECTOR ALGEBRA. KONSEPTO NG VECTOR
Kapag nag-aaral ng iba't ibang sangay ng pisika, may mga dami na ganap na natutukoy sa pamamagitan ng pagtatakda ng kanilang mga numerical na halaga, halimbawa, haba, lugar, masa, temperatura, atbp. Ang ganitong mga halaga ay tinatawag na scalar. Gayunpaman, bilang karagdagan sa kanila, mayroon ding mga dami, para sa pagpapasiya kung saan, bilang karagdagan sa numerical na halaga, kinakailangan ding malaman ang kanilang direksyon sa espasyo, halimbawa, ang puwersa na kumikilos sa katawan, ang bilis at pagbilis. ng katawan kapag gumagalaw ito sa kalawakan, ang lakas ng magnetic field sa isang partikular na punto sa espasyo at iba pa. Ang ganitong mga dami ay tinatawag na mga dami ng vector.
Ipakilala natin ang isang mahigpit na kahulugan.
Direksyon na segment Tawagan natin ang isang segment, na nauugnay sa mga dulo kung saan alam kung alin sa kanila ang una at alin ang pangalawa.

Vector tinatawag ang isang nakadirekta na segment, na may tiyak na haba, i.e. Ito ay isang segment ng isang tiyak na haba, kung saan ang isa sa mga puntong naglilimita dito ay kinuha bilang simula, at ang pangalawa - bilang pagtatapos. Kung A ay ang simula ng vector, B ay ang katapusan nito, kung gayon ang vector ay tinutukoy ng simbolo, bilang karagdagan, ang vector ay madalas na tinutukoy ng isang solong titik . Sa figure, ang vector ay ipinahiwatig ng isang segment, at ang direksyon nito sa pamamagitan ng isang arrow.
modyul o haba vector ay tinatawag na haba ng nakadirekta na segment na tumutukoy dito. Tinutukoy ng || o ||.
Ang tinatawag na zero vector, na ang simula at pagtatapos ay nagtutugma, ay tatawagin din bilang mga vector. Ito ay minarkahan. Ang zero vector ay walang tiyak na direksyon at ang modulus nito ay katumbas ng zero ||=0.
Vectors at tinatawag na collinear kung sila ay matatagpuan sa parehong linya o sa parallel na linya. Sa kasong ito, kung ang mga vector at ay pantay na nakadirekta, isusulat namin ang , kabaligtaran.
Ang mga vector na matatagpuan sa mga tuwid na linya na parallel sa parehong eroplano ay tinatawag coplanar.
Dalawang vector at tinatawag pantay kung sila ay collinear, may parehong direksyon, at pantay ang haba. Sa kasong ito, isulat ang .
Ito ay sumusunod mula sa kahulugan ng pagkakapantay-pantay ng mga vector na ang isang vector ay maaaring ilipat parallel sa sarili nito sa pamamagitan ng paglalagay ng pinagmulan nito sa anumang punto sa espasyo.
Halimbawa .
MGA LINEAR NA OPERASYON SA MGA VECTOR
Ang produkto ng isang vector sa pamamagitan ng isang numerong λ ay isang bagong vector tulad na:
Ang produkto ng isang vector at isang numerong λ ay tinutukoy ng .

Halimbawa, mayroong isang vector na tumuturo sa parehong direksyon ng vector at may haba na kalahati ng haba ng vector.
Ang ipinakilala na operasyon ay may mga sumusunod na katangian:
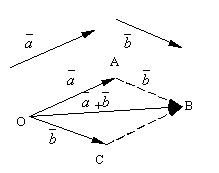
Hayaan at maging dalawang arbitrary vectors. Kumuha ng isang arbitrary na punto O at bumuo ng isang vector. Pagkatapos nito, mula sa punto A isantabi ang vector. Ang vector na nagkokonekta sa simula ng unang vector sa dulo ng pangalawa ay tinatawag kabuuan ng mga vector na ito at ipinapahiwatig ![]() .
.

Tinatawag ang formulated definition ng vector addition tuntunin ng paralelogram, dahil ang parehong kabuuan ng mga vector ay maaaring makuha tulad ng sumusunod. Itabi sa punto O mga vector at . Bumuo ng paralelogram sa mga vector na ito OABC. Dahil ang mga vectors, pagkatapos ay ang vector, na kung saan ay ang dayagonal ng parallelogram na iginuhit mula sa vertex O, ay malinaw naman ang kabuuan ng mga vectors .
Madaling suriin ang mga sumusunod na katangian ng pagdaragdag ng vector.
Ang isang vector collinear sa isang naibigay na vector , katumbas ng haba at magkasalungat na direksyon, ay tinatawag kabaligtaran vector para sa isang vector at tinutukoy ng . Ang kabaligtaran na vector ay maaaring isaalang-alang bilang resulta ng pagpaparami ng vector sa bilang na λ = –1: .
Paano magpasok ng mga mathematical formula sa site?
Kung sakaling kailanganin mong magdagdag ng isa o dalawang mathematical formula sa isang web page, kung gayon ang pinakamadaling paraan upang gawin ito ay tulad ng inilarawan sa artikulo: ang mga mathematical formula ay madaling naipasok sa site sa anyo ng mga larawan na awtomatikong nabubuo ng Wolfram Alpha. Bilang karagdagan sa pagiging simple, ang unibersal na paraan na ito ay makakatulong na mapabuti ang visibility ng site sa mga search engine. Ito ay gumagana nang mahabang panahon (at sa tingin ko ito ay gagana magpakailanman), ngunit ito ay luma na sa moral.
Kung, sa kabilang banda, palagi kang gumagamit ng mga mathematical formula sa iyong site, pagkatapos ay inirerekomenda ko na gumamit ka ng MathJax, isang espesyal na JavaScript library na nagpapakita ng mathematical notation sa mga web browser gamit ang MathML, LaTeX, o ASCIIMathML markup.
Mayroong dalawang paraan upang simulan ang paggamit ng MathJax: (1) gamit ang isang simpleng code, maaari mong mabilis na ikonekta ang isang MathJax script sa iyong site, na awtomatikong mai-load mula sa isang malayong server sa tamang oras (listahan ng mga server); (2) i-upload ang MathJax script mula sa isang malayuang server patungo sa iyong server at ikonekta ito sa lahat ng pahina ng iyong site. Ang pangalawang paraan ay mas kumplikado at nakakaubos ng oras at magbibigay-daan sa iyong mapabilis ang paglo-load ng mga pahina ng iyong site, at kung ang parent na MathJax server ay pansamantalang hindi magagamit sa ilang kadahilanan, hindi ito makakaapekto sa iyong sariling site sa anumang paraan. Sa kabila ng mga pakinabang na ito, pinili ko ang unang paraan, dahil ito ay mas simple, mas mabilis at hindi nangangailangan ng mga teknikal na kasanayan. Sundin ang aking halimbawa, at sa loob ng 5 minuto ay magagamit mo ang lahat ng mga tampok ng MathJax sa iyong site.
Maaari mong ikonekta ang script ng MathJax library mula sa isang malayuang server gamit ang dalawang opsyon sa code na kinuha mula sa pangunahing website ng MathJax o mula sa pahina ng dokumentasyon:
Ang isa sa mga pagpipilian sa code na ito ay dapat na kopyahin at i-paste sa iyong web page code, mas mabuti sa pagitan ng mga tag at o pagkatapos mismo ng tag. Ayon sa unang opsyon, ang MathJax ay naglo-load nang mas mabilis at nagpapabagal sa pahina nang mas kaunti. Ngunit awtomatikong sinusubaybayan at nilo-load ng pangalawang opsyon ang pinakabagong bersyon ng MathJax. Kung ilalagay mo ang unang code, kakailanganin itong i-update sa pana-panahon. Kung i-paste mo ang pangalawang code, ang mga pahina ay maglo-load nang mas mabagal, ngunit hindi mo kailangang patuloy na subaybayan ang mga update sa MathJax.
Ang pinakamadaling paraan upang ikonekta ang MathJax ay nasa Blogger o WordPress: sa control panel ng site, magdagdag ng widget na idinisenyo upang magpasok ng third-party na JavaScript code, kopyahin ang una o pangalawang bersyon ng load code sa itaas, at ilagay ang widget na mas malapit sa ang simula ng template (sa pamamagitan ng paraan, ito ay hindi kinakailangan sa lahat , dahil ang MathJax script ay na-load nang asynchronously). Iyon lang. Ngayon matutunan ang MathML, LaTeX, at ASCIIMathML markup syntax at handa ka nang mag-embed ng mga math formula sa iyong mga web page.
Ang anumang fractal ay binuo ayon sa isang tiyak na panuntunan, na patuloy na inilalapat ng walang limitasyong bilang ng beses. Ang bawat ganoong oras ay tinatawag na isang pag-ulit.
Ang umuulit na algorithm para sa pagbuo ng isang Menger sponge ay medyo simple: ang orihinal na cube na may side 1 ay hinahati ng mga eroplanong parallel sa mga mukha nito sa 27 pantay na cube. Ang isang gitnang kubo at 6 na kubo na katabi nito kasama ang mga mukha ay tinanggal mula dito. Ito ay lumiliko ang isang set na binubuo ng 20 natitirang mas maliliit na cubes. Ang paggawa ng pareho sa bawat isa sa mga cube na ito, nakakakuha kami ng isang set na binubuo ng 400 mas maliliit na cube. Ang pagpapatuloy ng prosesong ito nang walang katapusan, nakukuha namin ang Menger sponge.
Ang eigenvector ng isang square matrix ay isa na, kapag pinarami ng isang ibinigay na matrix, ay nagreresulta sa isang collinear vector. Sa simpleng salita, kapag ang isang matrix ay pinarami ng eigenvector, ang huli ay nananatiling pareho, ngunit pinarami ng ilang numero.
KahuluganAng eigenvector ay isang non-zero vector V, na, kapag pinarami ng isang square matrix M, ay nagiging sarili nito, na nadagdagan ng ilang bilang na λ. Sa algebraic notation, ganito ang hitsura:
M × V = λ × V,
kung saan ang λ ay isang eigenvalue ng matrix M.
Isaalang-alang natin ang isang numerical na halimbawa. Para sa kaginhawahan ng pagsulat, ang mga numero sa matrix ay paghiwalayin ng isang semicolon. Sabihin nating mayroon tayong matrix:
- M = 0; 4;
- 6; 10.
I-multiply natin ito sa isang column vector:
- V = -2;
Kapag nagpaparami ng matrix sa isang column vector, nakakakuha din kami ng column vector. Sa mahigpit na wikang matematika, ang formula para sa pagpaparami ng 2 × 2 matrix sa isang column vector ay magiging ganito:
- M × V = M11 × V11 + M12 × V21;
- M21 x V11 + M22 x V21.
Ang ibig sabihin ng M11 ay ang elemento ng matrix M, na nakatayo sa unang hilera at unang hanay, at ang M22 ay ang elementong matatagpuan sa ikalawang hanay at ikalawang hanay. Para sa aming matrix, ang mga elementong ito ay M11 = 0, M12 = 4, M21 = 6, M22 10. Para sa isang column vector, ang mga halagang ito ay V11 = –2, V21 = 1. Ayon sa formula na ito, nakukuha namin ang sumusunod resulta ng produkto ng isang square matrix ng isang vector:
- M × V = 0 × (-2) + (4) × (1) = 4;
- 6 × (-2) + 10 × (1) = -2.
Para sa kaginhawahan, isinusulat namin ang column vector sa isang hilera. Kaya, pinarami namin ang square matrix sa vector (-2; 1), na nagreresulta sa vector (4; -2). Malinaw, ito ay ang parehong vector na pinarami ng λ = -2. Ang Lambda sa kasong ito ay nagsasaad ng eigenvalue ng matrix.
Ang eigenvector ng isang matrix ay isang collinear vector, iyon ay, isang bagay na hindi nagbabago ng posisyon nito sa espasyo kapag ito ay pinarami ng isang matrix. Ang konsepto ng collinearity sa vector algebra ay katulad ng term ng parallelism sa geometry. Sa geometric na interpretasyon, ang mga collinear vector ay parallel na nakadirekta na mga segment na may iba't ibang haba. Mula noong panahon ng Euclid, alam natin na ang isang linya ay may walang katapusang bilang ng mga linya na kahanay nito, kaya lohikal na ipagpalagay na ang bawat matrix ay may walang katapusang bilang ng eigenvectors.
Mula sa nakaraang halimbawa, makikita na ang parehong (-8; 4), at (16; -8), at (32, -16) ay maaaring eigenvectors. Ang lahat ng ito ay mga collinear vector na naaayon sa eigenvalue λ = -2. Kapag pinarami ang orihinal na matrix ng mga vector na ito, makakakuha pa rin tayo ng isang vector bilang isang resulta, na naiiba sa orihinal ng 2 beses. Iyon ang dahilan kung bakit, kapag nilulutas ang mga problema para sa paghahanap ng eigenvector, kinakailangan na maghanap lamang ng mga linearly independent na vector object. Kadalasan, para sa isang n × n matrix, mayroong n-th na bilang ng mga eigenvector. Ang aming calculator ay idinisenyo para sa pagsusuri ng mga second-order square matrice, kaya halos palaging dalawang eigenvector ang makikita bilang isang resulta, maliban kung sila ay nag-tutugma.
Sa halimbawa sa itaas, alam namin nang maaga ang eigenvector ng orihinal na matrix at biswal na tinutukoy ang numero ng lambda. Gayunpaman, sa pagsasagawa, ang lahat ay nangyayari sa kabaligtaran: sa simula mayroong mga eigenvalues at pagkatapos ay mga eigenvectors.
Algoritmo ng solusyonTingnan natin muli ang orihinal na matrix M at subukang hanapin ang parehong eigenvectors nito. Kaya ang matrix ay ganito ang hitsura:
- M = 0; 4;
- 6; 10.
Upang magsimula, kailangan nating matukoy ang eigenvalue λ, kung saan kailangan nating kalkulahin ang determinant ng sumusunod na matrix:
- (0 − λ); 4;
- 6; (10 − λ).
Ang matrix na ito ay nakuha sa pamamagitan ng pagbabawas ng hindi kilalang λ mula sa mga elemento sa pangunahing dayagonal. Ang determinant ay tinutukoy ng karaniwang formula:
- detA = M11 × M21 − M12 × M22
- detA = (0 − λ) × (10 − λ) − 24
Dahil hindi dapat zero ang ating vector, kinukuha natin ang resultang equation bilang linearly dependent at itinutumbas ang ating determinant detA sa zero.
(0 − λ) × (10 − λ) − 24 = 0
Buksan natin ang mga bracket at kunin ang katangian na equation ng matrix:
λ 2 − 10λ − 24 = 0
Ito ay isang karaniwang quadratic equation na kailangang lutasin sa mga tuntunin ng discriminant.
D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196
Ang ugat ng discriminant ay sqrt(D) = 14, kaya λ1 = -2, λ2 = 12. Ngayon para sa bawat halaga ng lambda, kailangan nating maghanap ng eigenvector. Ipahayag natin ang mga coefficient ng system para sa λ = -2.
- M − λ × E = 2; 4;
- 6; 12.
Sa formula na ito, ang E ay ang identity matrix. Batay sa nakuha na matrix, bumubuo kami ng isang sistema ng mga linear na equation:
2x + 4y = 6x + 12y
kung saan ang x at y ay mga elemento ng eigenvector.
Kolektahin natin ang lahat ng X sa kaliwa at lahat ng Y sa kanan. Malinaw - 4x = 8y. Hatiin ang expression sa - 4 at makuha ang x = -2y. Ngayon ay matutukoy natin ang unang eigenvector ng matrix sa pamamagitan ng pagkuha ng anumang mga halaga ng mga hindi alam (tandaan ang tungkol sa infinity ng mga linearly dependent eigenvectors). Kunin natin ang y = 1, pagkatapos ay x = -2. Samakatuwid, ang unang eigenvector ay mukhang V1 = (–2; 1). Bumalik sa simula ng artikulo. Ito ang vector object na pinarami namin ang matrix upang ipakita ang konsepto ng isang eigenvector.
Ngayon hanapin natin ang eigenvector para sa λ = 12.
- M - λ × E = -12; 4
- 6; -2.
Bumuo tayo ng parehong sistema ng mga linear na equation;
- -12x + 4y = 6x − 2y
- -18x = -6y
- 3x=y.
Ngayon kunin natin ang x = 1, kaya y = 3. Kaya, ang pangalawang eigenvector ay parang V2 = (1; 3). Kapag pina-multiply ang orihinal na matrix sa vector na ito, ang resulta ay palaging magiging parehong vector na pinarami ng 12. Kinukumpleto nito ang algorithm ng solusyon. Ngayon alam mo na kung paano manu-manong tukuyin ang isang eigenvector ng isang matrix.
- determinant;
- bakas, iyon ay, ang kabuuan ng mga elemento sa pangunahing dayagonal;
- ranggo, ibig sabihin, ang maximum na bilang ng mga linearly independent na row/column.
Gumagana ang programa ayon sa algorithm sa itaas, pinaliit ang proseso ng solusyon. Mahalagang ituro na sa programa ang lambda ay tinutukoy ng titik na "c". Tingnan natin ang isang numerical na halimbawa.
Halimbawa ng programaSubukan nating tukuyin ang mga eigenvector para sa sumusunod na matrix:
- M=5; 13;
- 4; 14.
Ipasok natin ang mga halagang ito sa mga cell ng calculator at makuha ang sagot sa sumusunod na form:
- Ranggo ng matrix: 2;
- Matrix determinant: 18;
- Matrix trace: 19;
- Pagkalkula ng Eigenvector: c 2 − 19.00c + 18.00 (characteristic equation);
- Pagkalkula ng Eigenvector: 18 (unang halaga ng lambda);
- Pagkalkula ng Eigenvector: 1 (pangalawang halaga ng lambda);
- Sistema ng mga equation ng vector 1: -13x1 + 13y1 = 4x1 − 4y1;
- Vector 2 equation system: 4x1 + 13y1 = 4x1 + 13y1;
- Eigenvector 1: (1; 1);
- Eigenvector 2: (-3.25; 1).
Kaya, nakakuha kami ng dalawang linearly independent eigenvectors.
KonklusyonAng linear algebra at analytic geometry ay mga karaniwang paksa para sa sinumang freshman sa engineering. Ang isang malaking bilang ng mga vector at matrice ay nakakatakot, at madaling magkamali sa gayong masalimuot na mga kalkulasyon. Ang aming programa ay magbibigay-daan sa mga mag-aaral na suriin ang kanilang mga kalkulasyon o awtomatikong lutasin ang problema sa paghahanap ng eigenvector. Mayroong iba pang mga linear algebra calculators sa aming catalog, gamitin ang mga ito sa iyong pag-aaral o trabaho.
Sa matrix A, kung mayroong isang numero l tulad na AX = lX.
Sa kasong ito, ang numero l ay tinatawag na eigenvalue ng operator (matrix A), na tumutugma sa vector X.
Sa madaling salita, ang eigenvector ay isang vector na, sa ilalim ng pagkilos ng isang linear operator, ay nagiging isang collinear vector, i.e. multiply lang sa ilang numero. Sa kabaligtaran, ang mga hindi wastong vector ay mas mahirap ibahin ang anyo.
Isinulat namin ang kahulugan ng eigenvector bilang isang sistema ng mga equation:
Ilipat natin ang lahat ng termino sa kaliwang bahagi:

Ang huling sistema ay maaaring isulat sa matrix form tulad ng sumusunod:
(A - lE)X \u003d O
Ang resultang sistema ay palaging may zero na solusyon X \u003d O. Ang mga ganitong sistema kung saan ang lahat ng mga libreng miyembro ay katumbas ng zero ay tinatawag na homogenous. Kung ang matrix ng naturang sistema ay parisukat, at ang determinant nito ay hindi katumbas ng zero, kung gayon ayon sa mga formula ng Cramer, palagi kaming makakakuha ng isang natatanging solusyon - zero. Mapapatunayan na ang sistema ay may mga non-zero na solusyon kung at kung ang determinant ng matrix na ito ay katumbas ng zero, i.e.
|A - lE| =  = 0
= 0
Ang equation na ito na may hindi kilalang l ay tinatawag na characteristic equation (characteristic polynomial) ng matrix A (linear operator).
Mapapatunayan na ang katangiang polynomial ng isang linear operator ay hindi nakasalalay sa pagpili ng batayan.
Halimbawa, hanapin natin ang mga eigenvalues at eigenvectors ng linear operator na ibinigay ng matrix A = .
Upang gawin ito, binubuo namin ang katangiang equation |А - lЕ| = ![]() \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; eigenvalues l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.
\u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; eigenvalues l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.
Upang mahanap ang eigenvectors, nilulutas namin ang dalawang sistema ng mga equation
(A + 5E) X = O
(A - 7E) X = O
Para sa una sa kanila, ang pinalawak na matrix ay kukuha ng form
![]() ,
,
kung saan x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, i.e. X (1) \u003d (- (2/3) s; s).
Para sa pangalawa sa kanila, ang pinalawak na matrix ay kukuha ng form
![]() ,
,
kung saan x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, i.e. X (2) \u003d ((2/3) s 1; s 1).
Kaya, ang eigenvectors ng linear operator na ito ay lahat ng vectors ng form (-(2/3)c; c) na may eigenvalue (-5) at lahat ng vectors ng form ((2/3)c 1 ; c 1) na may eigenvalue 7 .
Mapapatunayan na ang matrix ng operator A sa batayan na binubuo ng mga eigenvector nito ay dayagonal at may anyo:
 ,
,
kung saan ako ang mga eigenvalues ng matrix na ito.
Ang kabaligtaran ay totoo rin: kung ang matrix A sa ilang batayan ay dayagonal, kung gayon ang lahat ng mga vector ng batayan na ito ay magiging eigenvectors ng matrix na ito.
Mapapatunayan din na kung ang isang linear na operator ay may n pairwise na natatanging eigenvalues, kung gayon ang mga katumbas na eigenvectors ay linearly independent, at ang matrix ng operator na ito sa kaukulang batayan ay may diagonal na anyo.
Ipaliwanag natin ito sa nakaraang halimbawa. Kumuha tayo ng mga di-zero na halaga c at c 1 , ngunit ang mga vector X (1) at X (2) ay linearly independent, i.e. magiging batayan. Halimbawa, hayaan ang c \u003d c 1 \u003d 3, pagkatapos ay X (1) \u003d (-2; 3), X (2) \u003d (2; 3).
I-verify natin ang linear na kalayaan ng mga vector na ito:
12 ≠ 0. Sa bagong batayan na ito, ang matrix A ay kukuha ng anyong A * = .
Upang i-verify ito, ginagamit namin ang formula A * = C -1 AC. Hanapin muna natin ang C -1.
C -1 = ![]() ;
;

Ang parisukat na anyo na f (x 1, x 2, x n) ng n variable ay ang kabuuan, ang bawat termino ay alinman sa parisukat ng isa sa mga variable, o ang produkto ng dalawang magkaibang variable, na kinuha sa isang tiyak na koepisyent: f ( x 1, x 2, x n ) = ![]() (a ij = a ji).
(a ij = a ji).
Ang matrix A, na binubuo ng mga coefficient na ito, ay tinatawag na quadratic form matrix. Ito ay palaging isang simetriko matrix (ibig sabihin, isang matrix na simetriko tungkol sa pangunahing dayagonal, a ij = a ji).
Sa matrix notation, ang quadratic form ay may anyong f(X) = X T AX, kung saan
Sa totoo lang

Halimbawa, isulat natin ang quadratic form sa matrix form.
Upang gawin ito, nakahanap kami ng isang matrix ng isang parisukat na anyo. Ang mga elemento ng dayagonal nito ay katumbas ng mga coefficient sa mga parisukat ng mga variable, at ang natitirang mga elemento ay katumbas ng kalahati ng kaukulang mga coefficient ng quadratic form. kaya lang

Hayaang makuha ang matrix-column ng mga variable X sa pamamagitan ng nondegenerate linear transformation ng matrix-column Y, i.e. X = CY, kung saan ang C ay isang non-degenerate matrix ng order n. Pagkatapos ay ang parisukat na anyo f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.
Kaya, sa ilalim ng isang non-degenerate linear transformation C, ang matrix ng parisukat na anyo ay tumatagal ng anyo: A * = C T AC.
Halimbawa, hanapin natin ang quadratic form f(y 1, y 2) na nakuha mula sa quadratic form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 sa pamamagitan ng linear transformation.

Ang isang parisukat na anyo ay tinatawag na canonical (ito ay may kanonikal na anyo ) kung ang lahat ng mga coefficient nito ay a ij = 0 para sa i ≠ j, i.e.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.
Ang matrix nito ay dayagonal.
Theorem (ang patunay ay hindi ibinigay dito). Anumang parisukat na anyo ay maaaring gawing kanonikal na anyo gamit ang isang non-degenerate linear transformation.
Halimbawa, bawasan natin sa canonical form ang quadratic form
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.
Upang gawin ito, piliin muna ang buong parisukat para sa variable na x 1:
f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2) ) 2 - 5x 2 2 - x 2 x 3.
Ngayon pipiliin namin ang buong parisukat para sa variable x 2:
f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.
Pagkatapos ang non-degenerate linear transformation y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 at y 3 \u003d x 3 ay nagdadala ng quadratic form na ito sa canonical form f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .
Tandaan na ang kanonikal na anyo ng isang parisukat na anyo ay hindi malinaw na tinukoy (ang parehong parisukat na anyo ay maaaring bawasan sa kanonikal na anyo sa iba't ibang paraan). Gayunpaman, ang mga canonical form na nakuha sa pamamagitan ng iba't ibang mga pamamaraan ay may ilang mga karaniwang katangian. Sa partikular, ang bilang ng mga termino na may positibong (negatibong) coefficient ng isang parisukat na anyo ay hindi nakasalalay sa kung paano binabawasan ang anyo sa form na ito (halimbawa, sa isinasaalang-alang na halimbawa ay palaging may dalawang negatibo at isang positibong koepisyent). Ang pag-aari na ito ay tinatawag na batas ng pagkawalang-galaw ng mga parisukat na anyo.
I-verify natin ito sa pamamagitan ng pagbabawas ng parehong quadratic form sa canonical form sa ibang paraan. Simulan natin ang pagbabago sa variable x 2:
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, kung saan y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6 ) x 3 at y 3 = x 1 . Dito, isang negatibong koepisyent -3 sa y 1 at dalawang positibong coefficient 3 at 2 sa y 2 at y 3 (at gamit ang isa pang paraan, nakakuha kami ng negatibong koepisyent (-5) sa y 2 at dalawang positibong koepisyent: 2 sa y 1 at 1/20 para sa y 3).
Dapat ding tandaan na ang ranggo ng isang matrix ng isang parisukat na anyo, na tinatawag na ranggo ng isang parisukat na anyo, ay katumbas ng bilang ng mga di-zero na coefficient ng canonical na anyo at hindi nagbabago sa ilalim ng mga linear na pagbabago.
Ang isang parisukat na anyo na f(X) ay tinatawag na positibo (negatibong) tiyak, kung para sa lahat ng mga halaga ng mga variable na hindi sabay-sabay na katumbas ng zero, ito ay positibo, i.e. f(X) > 0 (negatibo, ibig sabihin.
f(X)< 0).
Halimbawa, ang quadratic form f 1 (X) \u003d x 1 2 + x 2 2 ay positive definite, dahil ay ang kabuuan ng mga parisukat, at ang parisukat na anyo f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 ay negatibong tiyak, dahil kumakatawan ito ay maaaring katawanin bilang f 2 (X) \u003d - (x 1 - x 2) 2.
Sa karamihan ng mga praktikal na sitwasyon, medyo mas mahirap itatag ang sign-definiteness ng isang quadratic form, kaya isa sa mga sumusunod na theorems ang ginagamit para dito (binubalangkas namin ang mga ito nang walang mga patunay).
Teorama. Ang isang parisukat na anyo ay positibo (negatibo) na tiyak kung at kung ang lahat ng eigenvalues ng matrix nito ay positibo (negatibo).
Theorem (Sylvester's criterion). Ang isang parisukat na anyo ay positibong tiyak kung at kung ang lahat ng pangunahing menor de edad ng matris ng form na ito ay positibo.
Ang pangunahing (angular) minor ng k-th order ng matrix A ng n-th order ay ang determinant ng matrix, na binubuo ng mga unang k row at column ng matrix A ().
Tandaan na para sa mga negatibong tiyak na parisukat na anyo, ang mga palatandaan ng pangunahing mga menor de edad ay kahalili, at ang first-order na menor ay dapat na negatibo.
Halimbawa, sinusuri namin ang quadratic form f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 para sa sign-definiteness.
![]() = (2 - l)*
= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17; ![]() . Samakatuwid, ang parisukat na anyo ay positibong tiyak.
. Samakatuwid, ang parisukat na anyo ay positibong tiyak.
Paraan 2. Ang pangunahing menor ng unang pagkakasunud-sunod ng matrix A D 1 = a 11 = 2 > 0. Ang pangunahing menor ng pangalawang order D 2 = = 6 - 4 = 2 > 0. Samakatuwid, ayon sa pamantayang Sylvester, ang parisukat na anyo ay positibong tiyak.
Sinusuri namin ang isa pang quadratic form para sa sign-definiteness, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.
Paraan 1. Bumuo tayo ng isang matrix ng parisukat na anyo А = . Ang katangiang equation ay magkakaroon ng anyo ![]() = (-2 - l)*
= (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17; ![]() . Samakatuwid, ang parisukat na anyo ay negatibong tiyak.
. Samakatuwid, ang parisukat na anyo ay negatibong tiyak.
Paraan 2. Ang pangunahing minor ng unang pagkakasunud-sunod ng matrix A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Samakatuwid, ayon sa Sylvester criterion, ang parisukat na anyo ay negatibong tiyak (ang mga palatandaan ng pangunahing mga menor de edad ay kahalili, simula sa minus).
At bilang isa pang halimbawa, sinusuri namin ang quadratic form f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 para sa sign-definiteness.
Paraan 1. Bumuo tayo ng isang matrix ng parisukat na anyo А = . Ang katangiang equation ay magkakaroon ng anyo ![]() = (2 - l)*
= (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41; ![]() .
.
Ang isa sa mga numerong ito ay negatibo at ang isa ay positibo. Ang mga palatandaan ng eigenvalues ay iba. Samakatuwid, ang isang parisukat na anyo ay hindi maaaring maging negatibo o positibong tiyak, i.e. ang quadratic form na ito ay hindi sign-definite (maaari itong kumuha ng mga halaga ng anumang sign).
Paraan 2. Ang pangunahing minor ng unang order ng matrix A D 1 = a 11 = 2 > 0. Ang pangunahing minor ng pangalawang order D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).
