Matris örneklerinin özdeğerlerini ve özvektörlerini bulun. Matris karakteristik denklemi

HOMOJEN DOĞRUSAL DENKLEMLER SİSTEMİ

Homojen lineer denklemler sistemi, formun bir sistemidir.

Açıktır ki bu durumda , çünkü bu determinantlardaki sütunlardan birinin tüm elemanları sıfıra eşittir.

Bilinmeyenler formüllerle bulunduğundan , daha sonra Δ ≠ 0 olduğunda, sistemin benzersiz bir sıfır çözümü vardır x = y = z= 0. Bununla birlikte, birçok problemde homojen bir sistemin sıfırdan başka çözümleri olup olmadığı sorusu ilgi çekicidir.

Teorem. Bir lineer homojen denklemler sisteminin sıfırdan farklı bir çözümü olması için Δ ≠ 0 olması gerekli ve yeterlidir.

Yani, determinant Δ ≠ 0 ise, sistemin tek bir çözümü vardır. Δ ≠ 0 ise, lineer homojen denklemler sisteminin sonsuz sayıda çözümü vardır.

Örnekler

Özvektörler ve Matris Özdeğerleri

Bir kare matris verilsin , X yüksekliği matrisin sırasına denk gelen bir matris sütunudur. A. .

Birçok problemde, şu denklemi dikkate almak gerekir: X

burada λ bir sayıdır. Herhangi bir λ için bu denklemin sıfır çözümü olduğu açıktır.

Bu denklemin sıfırdan farklı çözümleri olan λ sayısına denir. özdeğer matrisler A, a X böyle λ denir için kendi vektörü matrisler A.

Matrisin özvektörünü bulalım A. Çünkü E∙X=X, o zaman matris denklemi şu şekilde yeniden yazılabilir: veya . Genişletilmiş formda, bu denklem bir lineer denklem sistemi olarak yeniden yazılabilir. Yok canım .

Ve bu nedenle

Böylece, koordinatları belirlemek için bir homojen lineer denklem sistemimiz var. x 1, x 2, x 3 vektör X. Sistemin sıfırdan farklı çözümlere sahip olması için sistemin determinantının sıfıra eşit olması gerekli ve yeterlidir.

Bu, λ için 3. dereceden bir denklemdir. denir karakteristik denklem matrisler A ve özdeğerleri λ belirlemeye yarar.

Her özdeğer λ bir özvektöre karşılık gelir X, koordinatları sistemden karşılık gelen λ değerinde belirlenir.

Örnekler

VEKTÖR CEBİR. VEKTÖR KONSEPTİ

Fiziğin çeşitli dallarını incelerken, örneğin uzunluk, alan, kütle, sıcaklık vb. gibi sayısal değerleri ayarlanarak tamamen belirlenen nicelikler vardır. Bu tür değerlere skaler denir. Bununla birlikte, bunlara ek olarak, sayısal değere ek olarak, uzaydaki yönlerini, örneğin vücuda etki eden kuvveti, hızı ve ivmeyi bilmek için gerekli olan miktarlar da vardır. uzayda hareket ederken vücudun, uzayda belirli bir noktadaki manyetik alan kuvveti vb. Bu tür büyüklüklere vektörel büyüklükler denir.

Kesin bir tanım getirelim.

yönlü segment Hangisinin birinci, hangisinin ikinci olduğu bilinen uçlarına göre bir segment diyelim.

Vektör belirli bir uzunluğa sahip yönlendirilmiş bir segment denir, yani. Bu, onu sınırlayan noktalardan birinin başlangıç, ikincisinin ise son olarak alındığı belirli bir uzunlukta bir segmenttir. Eğer bir A vektörün başlangıcıdır, B sonu ise, vektör sembolü ile gösterilir, ayrıca vektör genellikle tek bir harf ile gösterilir. Şekilde vektör bir segmentle ve yönü bir okla gösterilmiştir.

modül veya uzun vektör, onu tanımlayan yönlendirilmiş parçanın uzunluğu olarak adlandırılır. || ile gösterilir veya ||.

Başı ve sonu çakışan sözde sıfır vektörü de vektörler olarak anılacaktır. İşaretlidir. Sıfır vektörünün belirli bir yönü yoktur ve modülü sıfır ||=0'a eşittir.

Vektörler ve denir doğrusal aynı hatta veya paralel hatlarda bulunuyorlarsa. Bu durumda, vektörler ve yönler eşitse, zıt olarak yazacağız.

Aynı düzleme paralel doğrular üzerinde bulunan vektörlere denir. aynı düzlemde.

İki vektör ve denir eşit doğrusal iseler, aynı yöne sahiptirler ve uzunlukları eşittir. Bu durumda yazın.

Vektörlerin eşitliğinin tanımından, bir vektörün orijini uzayda herhangi bir noktaya yerleştirerek kendisine paralel hareket ettirilebileceği sonucu çıkar.

Örneğin.

VEKTÖRLERDE DOĞRUSAL OPERASYONLAR

Bir vektörü bir sayı ile çarpma.
Bir vektörün λ sayısıyla çarpımı yeni bir vektördür, öyle ki:

Bir vektörün ve bir λ sayısının çarpımı ile gösterilir.

Örneğin, vektörle aynı yönü gösteren ve vektörün iki katı uzunluğa sahip bir vektördür.

Girilen işlem aşağıdakilere sahiptir özellikleri:
Vektörlerin eklenmesi.
İki keyfi vektör olsun ve olsun. Keyfi bir nokta alın Ö ve bir vektör oluşturun. Bundan sonra, noktadan A vektörü bir kenara koyun. Birinci vektörün başlangıcını ikincinin sonuna bağlayan vektöre denir. toplam bu vektörler ve gösterilir .

Vektör eklemenin formüle edilmiş tanımına denir. paralelkenar kuralı, çünkü aynı vektör toplamı aşağıdaki gibi elde edilebilir. Noktadan bir kenara koy Ö vektörler ve . Bu vektörler üzerinde bir paralelkenar oluşturun OABC. Vektörler olduğundan, köşeden çizilen paralelkenarın köşegeni olan vektör Ö, açıkçası vektörlerin toplamı olacaktır .

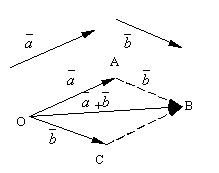
Aşağıdakileri kontrol etmek kolaydır vektör toplama özellikleri.
Vektörlerin farkı.
Belirli bir vektöre eşit uzunlukta ve zıt yönlü olan bir vektöre denir. karşısında bir vektör için vektör ve ile gösterilir. Zıt vektör, λ = –1: sayısı ile vektör çarpmasının sonucu olarak düşünülebilir.

Siteye matematiksel formüller nasıl eklenir?

Bir web sayfasına bir veya iki matematiksel formül eklemeniz gerekirse, bunu yapmanın en kolay yolu makalede anlatıldığı gibidir: matematiksel formüller Wolfram Alpha'nın otomatik olarak oluşturduğu resimler biçiminde siteye kolayca eklenir. Basitliğe ek olarak, bu evrensel yöntem, sitenin arama motorlarında görünürlüğünü artırmaya yardımcı olacaktır. Uzun süredir çalışıyor (ve sanırım sonsuza kadar da çalışacak), ancak ahlaki olarak modası geçmiş.

Sitenizde sürekli matematik formülleri kullanıyorsanız, MathML, LaTeX veya ASCIIMathML işaretlemesini kullanan web tarayıcılarında matematik gösterimini görüntüleyen özel bir JavaScript kitaplığı olan MathJax'ı kullanmanızı öneririm.

MathJax'i kullanmaya başlamanın iki yolu vardır: (1) basit bir kod kullanarak, sitenize hızlı bir şekilde bir MathJax betiği bağlayabilirsiniz, bu komut doğru zamanda uzak bir sunucudan otomatik olarak yüklenecektir (sunucu listesi); (2) MathJax komut dosyasını uzak bir sunucudan sunucunuza yükleyin ve sitenizin tüm sayfalarına bağlayın. İkinci yöntem daha karmaşık ve zaman alıcıdır ve sitenizin sayfalarının yüklenmesini hızlandırmanıza olanak tanır ve ana MathJax sunucusunun herhangi bir nedenle geçici olarak kullanılamaması durumunda bu, kendi sitenizi hiçbir şekilde etkilemeyecektir. Bu avantajlara rağmen, daha basit, daha hızlı ve teknik beceri gerektirmediği için ilk yöntemi seçtim. Örneğimi takip edin ve 5 dakika içinde MathJax'in tüm özelliklerini sitenizde kullanabileceksiniz.

MathJax kitaplığı komut dosyasını, ana MathJax web sitesinden veya belgeler sayfasından alınan iki kod seçeneğini kullanarak uzak bir sunucudan bağlayabilirsiniz:

Bu kod seçeneklerinden birinin kopyalanıp web sayfanızın koduna, tercihen etiketler arasına yapıştırılması gerekir. ve veya etiketten hemen sonra . İlk seçeneğe göre MathJax daha hızlı yüklenir ve sayfayı daha az yavaşlatır. Ancak ikinci seçenek, MathJax'in en son sürümlerini otomatik olarak izler ve yükler. İlk kodu eklerseniz, periyodik olarak güncellenmesi gerekecektir. İkinci kodu yapıştırırsanız, sayfalar daha yavaş yüklenir, ancak MathJax güncellemelerini sürekli olarak izlemeniz gerekmez.

MathJax'ı bağlamanın en kolay yolu Blogger veya WordPress'te: site kontrol panelinde, üçüncü taraf JavaScript kodunu eklemek için tasarlanmış bir widget ekleyin, yukarıda sunulan yükleme kodunun birinci veya ikinci sürümünü ona kopyalayın ve widget'ı daha yakına yerleştirin şablonun başına kadar (bu arada, MathJax betiği eşzamansız olarak yüklendiğinden bu hiç gerekli değildir). Bu kadar. Şimdi MathML, LaTeX ve ASCIIMathML biçimlendirme sözdizimini öğrenin ve matematik formüllerini web sayfalarınıza yerleştirmeye hazırsınız.

Herhangi bir fraktal, sürekli olarak sınırsız sayıda uygulanan belirli bir kurala göre oluşturulur. Böyle her bir zamana yineleme denir.

Bir Menger süngeri oluşturmak için yinelemeli algoritma oldukça basittir: 1 kenarı olan orijinal küp, yüzlerine paralel düzlemlerle 27 eşit kübe bölünür. Bir merkezi küp ve yüzleri boyunca ona bitişik 6 küp ondan çıkarılır. Geriye kalan 20 küçük küpten oluşan bir set ortaya çıkıyor. Bu küplerin her biri ile aynı şeyi yaparak, 400 küçük küpten oluşan bir set elde ederiz. Bu işleme süresiz devam ederek Menger süngeri elde ederiz.

Bir kare matrisin özvektörü, belirli bir matrisle çarpıldığında eşdoğrusal bir vektörle sonuçlanan bir matristir. Basit bir deyişle, bir matris bir özvektörle çarpıldığında, ikincisi aynı kalır, ancak bir sayı ile çarpılır.

Tanım

Bir özvektör, bir kare matris M ile çarpıldığında, bir λ sayısı kadar artan kendisi haline gelen sıfır olmayan bir V vektörüdür. Cebirsel gösterimde, bu şöyle görünür:

M × V = λ × V,

burada λ, M matrisinin bir özdeğeridir.

Sayısal bir örnek düşünelim. Yazma kolaylığı için matristeki sayılar noktalı virgülle ayrılacaktır. Diyelim ki bir matrisimiz var:

M = 0; dört;
6; 10.

Bunu bir sütun vektörü ile çarpalım:

V = -2;

Bir matrisi bir sütun vektörüyle çarparken, bir sütun vektörü de elde ederiz. Katı matematik dilinde, 2 × 2 matrisi bir sütun vektörüyle çarpma formülü şöyle görünür:

M × V = M11 × V11 + M12 × V21;
M21 x V11 + M22 x V21.

M11, ilk satır ve ilk sütunda bulunan M matrisinin elemanı ve M22 - ikinci satır ve ikinci sütunda bulunan eleman anlamına gelir. Matrisimiz için bu elemanlar M11 = 0, M12 = 4, M21 = 6, M22 10'dur. Bir sütun vektörü için bu değerler V11 = –2, V21 = 1'dir. Bu formüle göre aşağıdakileri elde ederiz. bir vektör ile kare matrisin çarpımının sonucu:

M × V = 0 × (-2) + (4) × (1) = 4;
6 × (-2) + 10 × (1) = -2.

Kolaylık sağlamak için sütun vektörünü bir satıra yazıyoruz. Böylece, kare matrisi vektör (-2; 1) ile çarparak vektörü (4; -2) elde ettik. Açıkçası, bu aynı vektörün λ = -2 ile çarpımıdır. Bu durumda Lambda, matrisin bir özdeğerini belirtir.

Bir matrisin özvektörü, doğrusal bir vektördür, yani bir matris ile çarpıldığında uzaydaki konumunu değiştirmeyen bir nesnedir. Vektör cebirindeki eşdoğrusallık kavramı, geometrideki paralellik terimine benzer. Geometrik yorumlamada, eşdoğrusal vektörler, farklı uzunluklarda paralel yönlendirilmiş parçalardır. Öklid zamanından beri, tek bir doğrunun kendisine paralel sonsuz sayıda doğruya sahip olduğunu biliyoruz, bu nedenle her matrisin sonsuz sayıda özvektöre sahip olduğunu varsaymak mantıklıdır.

Önceki örnekten, hem (-8; 4) hem de (16; -8) ve (32, -16) özvektörleri olabilir. Bütün bunlar, λ = -2 özdeğerine karşılık gelen eşdoğrusal vektörlerdir. Orijinal matrisi bu vektörlerle çarparken, sonuç olarak orijinalden 2 kat farklı bir vektör elde edeceğiz. Bu nedenle özvektör bulma problemlerini çözerken sadece lineer bağımsız vektör nesnelerini bulmak gerekir. Çoğu zaman, bir n × n matrisi için n'inci sayıda özvektör vardır. Hesaplayıcımız ikinci dereceden kare matrislerin analizi için tasarlanmıştır, bu nedenle çakışma durumları dışında neredeyse her zaman iki özvektör sonuç olarak bulunur.

Yukarıdaki örnekte, orijinal matrisin özvektörünü önceden biliyorduk ve lambda sayısını görsel olarak belirledik. Bununla birlikte, pratikte her şey tam tersi olur: başlangıçta özdeğerler vardır ve ancak o zaman özvektörler vardır.

Çözüm algoritması

Orijinal M matrisine tekrar bakalım ve her iki özvektörünü de bulmaya çalışalım. Böylece matris şöyle görünür:

M = 0; dört;
6; 10.

Başlangıç olarak, aşağıdaki matrisin determinantını hesaplamamız gereken λ özdeğerini belirlememiz gerekir:

(0 - λ); dört;
6; (10 - λ).

Bu matris, ana köşegen üzerindeki elemanlardan bilinmeyen λ çıkarılarak elde edilir. Belirleyici standart formülle belirlenir:

detA = M11 × M21 − M12 × M22
detA = (0 − λ) × (10 − λ) − 24

Vektörümüzün sıfır olmaması gerektiğinden, elde edilen denklemi lineer bağımlı olarak alırız ve determinantımız detA'yı sıfıra eşitleriz.

(0 − λ) × (10 − λ) − 24 = 0

Parantezleri açalım ve matrisin karakteristik denklemini alalım:

λ 2 − 10λ − 24 = 0

Bu, diskriminant cinsinden çözülmesi gereken standart bir ikinci dereceden denklemdir.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Diskriminantın kökü sqrt(D) = 14'tür, yani λ1 = -2, λ2 = 12. Şimdi her lambda değeri için bir özvektör bulmamız gerekiyor. λ = -2 için sistemin katsayılarını ifade edelim.

M − λ × E = 2; dört;
6; 12.

Bu formülde E birim matristir. Elde edilen matrise dayanarak, bir doğrusal denklem sistemi oluşturuyoruz:

2x + 4y = 6x + 12y

burada x ve y özvektörün elemanlarıdır.

Soldaki tüm X'leri ve sağdaki tüm Y'leri toplayalım. Açıkçası - 4x = 8y. İfadeyi - 4'e bölün ve x = -2y olsun. Şimdi bilinmeyenlerin herhangi bir değerini alarak matrisin ilk özvektörünü belirleyebiliriz (lineer bağımlı özvektörlerin sonsuzluğunu hatırlayın). y = 1, sonra x = -2 alalım. Bu nedenle, ilk özvektör V1 = (–2; 1) gibi görünür. Makalenin başına dön. Bir özvektör kavramını göstermek için matrisi çarptığımız bu vektör nesnesiydi.

Şimdi λ = 12 için özvektörü bulalım.

M - λ × E = -12; dört
6; -2.

Aynı lineer denklem sistemini oluşturalım;

-12x + 4y = 6x − 2y
-18x = -6y
3x=y.

Şimdi x = 1, dolayısıyla y = 3 alalım. Böylece, ikinci özvektör V2 = (1; 3) gibi görünür. Orijinal matrisi bu vektörle çarparken, sonuç her zaman aynı vektörün 12 ile çarpımı olacaktır. Bu, çözüm algoritmasını tamamlar. Artık bir matrisin özvektörünü manuel olarak nasıl tanımlayacağınızı biliyorsunuz.

belirleyici;
iz, yani ana köşegen üzerindeki elemanların toplamı;
rank, yani maksimum lineer bağımsız satır/sütun sayısı.

Program, çözüm sürecini en aza indirerek yukarıdaki algoritmaya göre çalışır. Programda lambda'nın "c" harfi ile gösterildiğini belirtmek önemlidir. Sayısal bir örneğe bakalım.

Program örneği

Aşağıdaki matris için özvektörleri tanımlamaya çalışalım:

M = 5; 13;
4; 14.

Bu değerleri hesap makinesinin hücrelerine girelim ve cevabı aşağıdaki formda alalım:

Matris sırası: 2;
Matris determinantı: 18;
Matris izi: 19;
Özvektör hesaplaması: c 2 − 19.00c + 18.00 (karakteristik denklem);
Özvektör hesaplaması: 18 (ilk lambda değeri);
Özvektör hesaplaması: 1 (ikinci lambda değeri);
Vektör 1 denklem sistemi: -13x1 + 13y1 = 4x1 − 4y1;
Vektör 2 denklem sistemi: 4x1 + 13y1 = 4x1 + 13y1;
Özvektör 1: (1; 1);
Özvektör 2: (-3.25; 1).

Böylece, lineer olarak bağımsız iki özvektör elde ettik.

Çözüm

Lineer cebir ve analitik geometri, mühendislikteki herhangi bir birinci sınıf öğrencisi için standart konulardır. Çok sayıda vektör ve matris ürkütücüdür ve bu tür hantal hesaplamalarda hata yapmak kolaydır. Programımız, öğrencilerin hesaplamalarını kontrol etmelerine veya bir özvektör bulma problemini otomatik olarak çözmelerine izin verecektir. Kataloğumuzda başka lineer cebir hesaplayıcılar da var, bunları çalışmanızda veya işinizde kullanın.

A matrisi ile, AX = lX olacak şekilde bir l sayısı varsa.

Bu durumda l sayısı denir. özdeğer X vektörüne karşılık gelen operatör (matris A).

Başka bir deyişle, bir özvektör, doğrusal bir operatörün etkisi altında, bir eşdoğrusal vektöre dönüşen bir vektördür, yani. sadece bir sayı ile çarpın. Buna karşılık, uygun olmayan vektörlerin dönüştürülmesi daha zordur.

Özvektörün tanımını bir denklem sistemi olarak yazıyoruz:

Tüm terimleri sol tarafa taşıyalım:

Son sistem matris formunda aşağıdaki gibi yazılabilir:

(A - lE)X \u003d O

Ortaya çıkan sistemin her zaman sıfır çözümü vardır X = O. Tüm serbest terimlerin sıfıra eşit olduğu bu tür sistemlere denir. homojen. Böyle bir sistemin matrisi kare ise ve determinantı sıfıra eşit değilse, Cramer formüllerine göre her zaman benzersiz bir çözüm elde edeceğiz - sıfır. Sistemin sıfır olmayan çözümlere sahip olduğu ancak ve ancak bu matrisin determinantı sıfıra eşitse, yani.

|A - lE| = = 0

Bilinmeyen l ile bu denklem denir karakteristik denklem (karakteristik polinom) matris A (doğrusal operatör).

Doğrusal bir operatörün karakteristik polinomunun temel seçimine bağlı olmadığı kanıtlanabilir.

Örneğin, A = matrisinin verdiği lineer operatörün özdeğerlerini ve özvektörlerini bulalım.

Bunu yapmak için, |А - lЕ| karakteristik denklemini oluşturuyoruz. = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; özdeğerler l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

Özvektörleri bulmak için iki denklem sistemini çözeriz.

(A + 5E) X = O

(A - 7E) X = O

Bunlardan ilki için genişletilmiş matris şu şekilde olacaktır:

nereden x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, yani. X (1) \u003d (- (2/3) s; s).

İkincisi için, genişletilmiş matris şu şekilde olacaktır:

nereden x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, yani. X (2) \u003d ((2/3) s 1; s 1).

Böylece, bu lineer operatörün özvektörleri, özdeğeri (-5) olan (-(2/3)c;c) formunun tüm vektörleri ve ((2/3)c 1 ; c 1) formunun tüm vektörleridir. özdeğer 7.

A operatörünün özvektörlerinden oluşan temeldeki matrisinin köşegen olduğu ve aşağıdaki forma sahip olduğu kanıtlanabilir:

burada ben bu matrisin özdeğerleriyim.

Bunun tersi de doğrudur: A matrisi bir bazda köşegen ise, bu temelin tüm vektörleri bu matrisin özvektörleri olacaktır.

Ayrıca, bir lineer operatörün n tane ikili farklı özdeğeri varsa, o zaman karşılık gelen özvektörlerin lineer olarak bağımsız olduğu ve bu operatörün karşılık gelen bazdaki matrisinin diyagonal bir forma sahip olduğu kanıtlanabilir.

Bunu bir önceki örnekle açıklayalım. Rasgele sıfır olmayan değerleri alalım c ve c 1 , ancak öyle ki X (1) ve X (2) vektörleri doğrusal olarak bağımsız, yani. bir temel oluşturacaktı. Örneğin, c \u003d c 1 \u003d 3, sonra X (1) \u003d (-2; 3), X (2) \u003d (2; 3) olsun.

Bu vektörlerin lineer bağımsızlığını doğrulayalım:

12 ≠ 0. Bu yeni temelde, A matrisi A * = biçimini alacaktır.

Bunu doğrulamak için A * = C -1 AC formülünü kullanıyoruz. Önce C-1'i bulalım.

C-1 = ;

ikinci dereceden formlar

ikinci dereceden biçim n değişkenlerden f (x 1, x 2, x n), her terimi değişkenlerden birinin karesi veya belirli bir katsayı ile alınan iki farklı değişkenin çarpımı olan toplam olarak adlandırılır: f (x 1 , x 2, x n) = (bir ij = bir ji).

Bu katsayılardan oluşan A matrisine denir. matris ikinci dereceden biçim. Her zaman simetrik matris (yani, ana köşegen etrafında simetrik bir matris, a ij = a ji).

Matris notasyonunda, ikinci dereceden form f(X) = X T AX formuna sahiptir, burada

Aslında

Örneğin, ikinci dereceden formu matris formunda yazalım.

Bunu yapmak için, ikinci dereceden bir formun matrisini buluyoruz. Köşegen elemanları, değişkenlerin karelerindeki katsayılara eşittir ve kalan elemanlar, ikinci dereceden formun karşılık gelen katsayılarının yarısına eşittir. Bu yüzden

X değişkenlerinin matris sütunu, Y matris sütununun dejenere olmayan bir doğrusal dönüşümü ile elde edilsin, yani. X = CY, burada C, n dereceli dejenere olmayan bir matristir. Sonra ikinci dereceden f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Böylece, dejenere olmayan bir doğrusal dönüşüm C altında, ikinci dereceden formun matrisi şu biçimi alır: A * = C T AC.

Örneğin, ikinci dereceden f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 formundan lineer bir dönüşümle elde edilen ikinci dereceden f(y 1, y 2) formunu bulalım.

İkinci dereceden forma denir kanonik(O var kanonik görünüm) i ≠ j için tüm katsayıları a ij = 0 ise, yani.
f(x 1, x 2, x n) = bir 11 x 1 2 + bir 22 x 2 2 + bir nn x n 2 =.

Matrisi köşegendir.

teorem(kanıt burada verilmemiştir). Herhangi bir ikinci dereceden form, dejenere olmayan bir doğrusal dönüşüm kullanılarak kanonik bir forma indirgenebilir.

Örneğin, ikinci dereceden formu kanonik forma indirgeyelim.
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Bunu yapmak için önce x 1 değişkeninin tam karesini seçin:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3.

Şimdi x 2 değişkeni için tam kareyi seçiyoruz:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Ardından, dejenere olmayan doğrusal dönüşüm y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 ve y 3 \u003d x 3 bu ikinci dereceden formu kanonik f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

İkinci dereceden bir formun kurallı biçiminin belirsiz bir şekilde tanımlandığına dikkat edin (aynı ikinci dereceden biçim, farklı şekillerde kurallı biçime indirgenebilir). Ancak çeşitli yöntemlerle elde edilen kanonik formların bir takım ortak özellikleri vardır. Özellikle, ikinci dereceden bir formun pozitif (negatif) katsayılarına sahip terimlerin sayısı, formun bu forma nasıl indirgendiğine bağlı değildir (örneğin, ele alınan örnekte, her zaman iki negatif ve bir pozitif katsayı olacaktır). Bu özelliğe ikinci dereceden formların eylemsizlik yasası denir.

Aynı ikinci dereceden formu kanonik forma farklı bir şekilde indirgeyerek bunu doğrulayalım. Dönüşüme x 2 değişkeni ile başlayalım:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, burada y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6 ) x 3 ve y3 = x 1 . Burada, y 1'de negatif bir katsayı -3 ve y 2 ve y 3'te iki pozitif katsayı 3 ve 2 (ve başka bir yöntem kullanarak, y 2'de negatif bir katsayı (-5) ve iki pozitif katsayı elde ettik: y 1'de 2 ve y 3) için 1/20.

Ayrıca, ikinci dereceden bir formun matrisinin sıralamasının, adı verilen ikinci dereceden formun sıralaması, kanonik formun sıfır olmayan katsayılarının sayısına eşittir ve doğrusal dönüşümler altında değişmez.

İkinci dereceden f(X) formuna denir olumlu (olumsuz) belirli, aynı anda sıfıra eşit olmayan değişkenlerin tüm değerleri için pozitifse, yani. f(X) > 0 (negatif, yani
f(X)< 0).

Örneğin, ikinci dereceden f 1 (X) \u003d x 1 2 + x 2 2 formu pozitif tanımlıdır, çünkü karelerin toplamıdır ve ikinci dereceden f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 negatif tanımlıdır, çünkü temsil eder f 2 (X) \u003d - (x 1 - x 2) 2 olarak temsil edilebilir.

Çoğu pratik durumda, ikinci dereceden bir formun işaret kesinliğini kurmak biraz daha zordur, bu nedenle aşağıdaki teoremlerden biri bunun için kullanılır (bunları ispat olmadan formüle ederiz).

teorem. İkinci dereceden bir form, ancak ve ancak matrisinin tüm özdeğerleri pozitif (negatif) ise pozitif (negatif) kesindir.

teorem(Sylvester'ın kriteri). İkinci dereceden bir form, ancak ve ancak bu formun matrisinin tüm asal minörleri pozitifse pozitif tanımlıdır.

Majör (köşe) minör n'inci sıradaki A matrisinin k'inci sırasına, matrisin A () ilk k satırından ve sütunlarından oluşan matrisin determinantı denir.

Negatif-belirli ikinci dereceden formlar için, asal minörlerin işaretleri değişkendir ve birinci dereceden minör negatif olmalıdır.

Örneğin, işaret kesinliği için ikinci dereceden f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 formunu inceleriz.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. Bu nedenle, ikinci dereceden form pozitif tanımlıdır.

Yöntem 2. Matrisin birinci mertebesinden ana minör A D 1 = a 11 = 2 > 0. İkinci mertebeden ana minör D 2 = = 6 - 4 = 2 > 0. Bu nedenle Sylvester kriterine göre, ikinci dereceden form pozitif tanımlıdır.

İşaret kesinliği için başka bir ikinci dereceden formu inceliyoruz, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Yöntem 1. İkinci dereceden form А = olan bir matris oluşturalım. Karakteristik denklem forma sahip olacaktır = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Bu nedenle, ikinci dereceden form negatif tanımlıdır.

Yöntem 2. Matrisin birinci mertebesinden ana minör A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Bu nedenle, Sylvester kriterine göre, ikinci dereceden form negatif tanımlıdır (asıl küçüklerin işaretleri eksiden başlayarak değişir).

Ve başka bir örnek olarak, işaret kesinliği için ikinci dereceden f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 formunu inceliyoruz.

Yöntem 1. İkinci dereceden form А = olan bir matris oluşturalım. Karakteristik denklem forma sahip olacaktır = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Bu sayılardan biri negatif diğeri pozitiftir. Özdeğerlerin işaretleri farklıdır. Bu nedenle, ikinci dereceden bir form ne negatif ne de pozitif tanımlı olamaz, yani. bu ikinci dereceden form, işaret tanımlı değildir (herhangi bir işaretin değerlerini alabilir).

Yöntem 2. Matrisin birinci mertebesinin ana minör A D 1 = a 11 = 2 > 0. İkinci mertebenin ana minör D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).