የኦፕሬተሩን ኢጂን እሴቶች ያግኙ። Eigenvalues ​​(ቁጥሮች) እና eigenvectors። የመፍትሄ ምሳሌዎች

ሰያፍ ማትሪክስ በጣም ቀላሉ መዋቅር አላቸው። ጥያቄው የሚነሳው የመስመራዊ ኦፕሬተር ማትሪክስ ሰያፍ ቅርጽ ያለውበትን መሠረት ማግኘት ይቻል እንደሆነ ነው። እንዲህ ዓይነቱ መሠረት አለ.
መስመራዊ ቦታ ይሰጠን R n እና መስመራዊ ኦፕሬተር በእሱ ውስጥ የሚሰራ; በዚህ ሁኔታ ኦፕሬተር A R nን ወደ ራሱ ይወስዳል, ማለትም, A: R n → R n .

ፍቺ ዜሮ ያልሆነ ቬክተር ኦፕሬተሩ ኤ ወደ ኮሊኔር ቬክተር ከተተረጎመ የኦፕሬተሩ ኢጂንቬክተር ይባላል። ቁጥሩ λ ከኢጂንቬክተር ጋር የሚዛመደው የኦፕሬተር ኤ ኢጂንቫል ወይም ኢጂንቫል ይባላል።
እስቲ አንዳንድ የ eigenvalues ​​እና eigenvectors ባህሪያትን እናስተውል።
1. ማንኛውም የ eigenvectors የመስመር ጥምረት ኦፕሬተር ሀ ከተመሳሳይ ኢጂንቫልዩ λ ጋር የሚዛመድ ኢጂንቬክተር ተመሳሳይ ኢጂን ዋጋ ያለው ነው።
2. Eigenvectors ኦፕሬተር ሀ ከጥንዶች ጋር የተለያዩ ኢጂን እሴቶች λ 1 ፣ λ 2 ፣… ፣ λ m በመስመር ገለልተኛ ናቸው።
3. የ eigenvalues ​​λ 1 = λ 2 = λ m = λ ከሆነ፣ ኢጂንቫልዩ λ ከ m የመስመር ላይ ገለልተኛ ኢኢጀንቬክተሮች ጋር ይዛመዳል።

ስለዚህ, n መስመራዊ ገለልተኛ eigenvectors አሉ ከሆነ , ከተለያዩ eigenvalues ​​λ 1, λ 2, ..., λ n ጋር የሚዛመድ, ከዚያም እነሱ በመስመር ላይ ገለልተኛ ናቸው, ስለዚህ, እንደ የቦታው መሠረት ሊወሰዱ ይችላሉ R n. የሊኒየር ኦፕሬተር ሀ ማትሪክስ ቅርፅን በ eigenvectors መሠረት እናገኝለት ፣ ለዚህም ከዋኝ ሀ ጋር በቬክተሮች ላይ እንሰራለን ። ከዚያም .
ስለዚህ የመስመራዊ ኦፕሬተር ሀ በ eigenvectors መሠረት ያለው ማትሪክስ ሰያፍ ቅርፅ አለው ፣ እና የኦፕሬተሩ ሀ ኢ-እሴቶቹ በዲያግናል በኩል ናቸው።
ማትሪክስ ሰያፍ ቅርጽ ያለውበት ሌላ መሠረት አለ? የዚህ ጥያቄ መልስ የሚሰጠው በሚከተለው ቲዎሪ ነው።

ቲዎረም. በመሰረቱ (i = 1..n) ውስጥ ያለው የመስመር ኦፕሬተር ሀ ማትሪክስ ሰያፍ ቅርጽ ያለው ከሆነ እና ሁሉም የመሠረቱ ቬክተሮች የኦፕሬተሩ ኤ ኢጂንቬክተሮች ከሆኑ ብቻ ነው።

eigenvalues ​​እና eigenvectors ለማግኘት ደንብ

. (*)

(1)
የት - መስመራዊ ኦፕሬተር ማትሪክስ.

ስርዓት (1) መወሰኑ ከዜሮ ጋር እኩል ከሆነ ዜሮ ያልሆነ መፍትሄ አለው።

ምሳሌ 12. መስመራዊ ኦፕሬተር ሀ በሕጉ መሠረት በ R 3 ውስጥ ይሠራል ፣ x 1 ፣ x 2 ፣ .. ፣ x n መሠረት ላይ የቬክተር መጋጠሚያዎች ናቸው ። , , . የዚህን ኦፕሬተር ኢጂንቫሉስ እና ኢጂንቬክተሮችን ያግኙ።
መፍትሄ። የዚህን ኦፕሬተር ማትሪክስ እንገነባለን-
.
የኢጂንቬክተሮች መጋጠሚያዎችን ለመወሰን ስርዓት እንፈጥራለን-

የባህሪ እኩልታ አዘጋጅተናል እና እንፈታዋለን፡-

.
λ 1፣2 = -1፣ λ 3 = 3።
λ = -1ን ወደ ስርዓቱ በመተካት፡-
ወይም
ምክንያቱም , ከዚያም ሁለት ጥገኛ ተለዋዋጮች እና አንድ ነጻ ተለዋዋጭ አሉ.
x 1 ነፃ ያልታወቀ ይሁን ይህንን ስርዓት በማንኛውም መንገድ እንፈታዋለን እና የዚህን ስርዓት አጠቃላይ መፍትሄ እናገኛለን፡ የመፍትሄው መሰረታዊ ስርዓት አንድ መፍትሄን ያቀፈ ነው, ምክንያቱም n - r = 3 - 2 = 1.
የ eigenvectors ስብስብ ከ eigenvalue λ = -1 ጋር የሚዛመደው ቅጽ አለው:, x 1 ከዜሮ ሌላ ማንኛውም ቁጥር ነው. ከዚህ ስብስብ አንድ ቬክተር እንምረጥ ለምሳሌ x 1 = 1 በማስቀመጥ። .
በተመሳሳዩ ምክንያት፣ ኢጂንቬክተር ከኢጂንቫልዩ λ = 3 ጋር የሚዛመድ ሆኖ እናገኘዋለን፡ .
በጠፈር R 3 ውስጥ, መሰረቱ ሶስት ቀጥተኛ ገለልተኛ የሆኑ ቬክተሮችን ያቀፈ ነው, ነገር ግን ሁለት ቀጥተኛ ገለልተኛ ኢጂንቬክተሮችን ብቻ ተቀብለናል, ይህም በ R 3 ውስጥ ያለው መሠረት ሊዘጋጅ አይችልም. በመሆኑም የመስመራዊ ኦፕሬተርን ማትሪክስ A ወደ ሰያፍ ቅርጽ መቀነስ አንችልም።

ምሳሌ 13. ማትሪክስ ተሰጥቶታል። .
1. ቬክተሩን ያረጋግጡ የማትሪክስ ኢጂንቬክተር ነው ሀ. ከዚህ ኢጂንቬክተር ጋር የሚዛመደውን ኢጂንቫሉ ያግኙ።
2. ማትሪክስ A ሰያፍ ቅርጽ ያለውበትን መሠረት ይፈልጉ።
መፍትሄ።
1. ከሆነ፣ እንግዲያውስ ኢጂንቬክተር ነው።

.
ቬክተር (1፣ 8፣ -1) ኢጂንቬክተር ነው። Eigenvalue λ = -1.
ማትሪክስ ኢጂንቬክተሮችን ባካተተ መሰረት ሰያፍ ቅርጽ አለው። ከመካከላቸው አንዱ ታዋቂ ነው. የቀረውን እንፈልግ።
ከስርአቱ ኢጂንቬክተሮችን እንፈልጋለን፡-

የባህሪ እኩልታ፡- ;
(3 + λ) [-2 (2-λ) (2+λ)+3] = 0; (3+λ) (λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
ኢጂንቬክተሩን ከ eigenvalue λ = -3 ጋር የሚዛመድን እንፈልግ፡-

የዚህ ስርዓት ማትሪክስ ደረጃ ሁለት እና ከማይታወቁት ቁጥር ጋር እኩል ነው, ስለዚህ ይህ ስርዓት ዜሮ መፍትሄ ብቻ x 1 = x 3 = 0. x 2 እዚህ ከዜሮ ሌላ ሊሆን ይችላል, ለምሳሌ, x 2 = 1. ስለዚህ, ቬክተር (0,1,0) ከ λ = -3 ጋር የሚመጣጠን eigenvector ነው. እስቲ እንፈትሽ፡
.
λ = 1 ከሆነ, ስርዓቱን እናገኛለን
የማትሪክስ ደረጃ ሁለት ነው. የመጨረሻውን እኩልታ እናቋርጣለን.
x 3 ነፃ የማይታወቅ ይሁን። ከዚያም x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
x 3 = 1ን ስናስብ፣ አለን (-3፣-9፣1) - eigenvector ከ eigenvalue λ = 1 ጋር የሚዛመድ።

.
የ eigenvalues ​​እውነተኛ እና የተለዩ ስለሆኑ ከእነሱ ጋር የሚዛመዱ ቬክተሮች በመስመር ላይ ገለልተኛ ናቸው, ስለዚህ በ R 3 ውስጥ እንደ መሰረት ሊወሰዱ ይችላሉ. በመሆኑም, መሠረት ውስጥ , , ማትሪክስ A ቅጽ አለው:
.
እያንዳንዱ የመስመር ኦፕሬተር A:R n → R n ወደ ሰያፍ ቅርጽ ሊቀንስ አይችልም ፣ ምክንያቱም ለአንዳንድ መስመራዊ ኦፕሬተሮች ከ n መስመራዊ ገለልተኛ ኢጂንቬክተሮች ያነሱ ሊሆኑ ይችላሉ። ሆኖም ፣ ማትሪክስ ተመሳሳይ ከሆነ ፣ የብዝሃነት m የባህሪ እኩልታ ስር በትክክል ከ m መስመራዊ ገለልተኛ ቫክተሮች ጋር ይዛመዳል።

ፍቺ ሲሜትሪክ ማትሪክስ ከዋናው ዲያግናል ጋር የሚመሳሰሉ ንጥረ ነገሮች እኩል የሆነበት ካሬ ማትሪክስ ነው ፣ ማለትም ፣ በውስጡ።
ማስታወሻዎች. 1. ሁሉም የሲሜትሪክ ማትሪክስ eigenvalues ​​እውን ናቸው።
2. ከተለያዩ የኢጂን እሴቶች ጋር የሚዛመደው የሲሜትሪክ ማትሪክስ ኢጂንቬክተሮች ኦርቶጎን ናቸው።
ከተጠኑት መሳሪያዎች ከበርካታ አፕሊኬሽኖች አንዱ እንደመሆናችን መጠን የሁለተኛ ደረጃ ኩርባ አይነት የመወሰን ችግርን እንመለከታለን።

Eigenvalues ​​(ቁጥሮች) እና eigenvectors።
የመፍትሄዎች ምሳሌዎች

እራስህን ሁን

ከሁለቱም እኩልታዎች እንደሚከተለው ነው.

እንግዲህ እናስቀምጠው፡- .

ከዚህ የተነሳ: - ሁለተኛ eigenvector.

የውሳኔውን ጠቃሚ ነጥቦች እንደግመዋለን፡-

- የተገኘው ስርዓት በእርግጥ አጠቃላይ መፍትሄ አለው (እኩልታዎቹ በመስመር ላይ ጥገኛ ናቸው);

- "y" ኢንቲጀር እንዲሆን እና የመጀመሪያው "x" መጋጠሚያ ኢንቲጀር, አወንታዊ እና በተቻለ መጠን ትንሽ እንዲሆን እንመርጣለን.

- የተወሰነው መፍትሔ የስርዓቱን እያንዳንዱን እኩልነት እንደሚያሟላ እናረጋግጣለን።

መልስ .

በቂ መካከለኛ “የፍተሻ ነጥቦች” ነበሩ፣ ስለዚህ እኩልነትን ማረጋገጥ በመርህ ደረጃ አላስፈላጊ ነው።

በተለያዩ የመረጃ ምንጮች የ eigenvectors መጋጠሚያዎች ብዙውን ጊዜ የሚጻፉት በአምዶች ሳይሆን በመደዳ ነው፣ ለምሳሌ፡- (እና እውነቱን ለመናገር እኔ ራሴ በመስመሮች ለመጻፍ ልምዳለሁ). ይህ አማራጭ ተቀባይነት ያለው ነው, ነገር ግን ከርዕሱ አንጻር መስመራዊ ለውጦችበቴክኒካዊ ሁኔታ ለመጠቀም የበለጠ ምቹ አምድ ቬክተሮች.

ምናልባት መፍትሄው ለእርስዎ በጣም ረጅም መስሎ ይታይዎት ይሆናል, ነገር ግን ይህ የሆነበት ምክንያት የመጀመሪያውን ምሳሌ በዝርዝር ስለገለጽኩ ብቻ ነው.

ምሳሌ 2

ማትሪክስ

በራሳችን እናሰልጥን! በትምህርቱ መጨረሻ ላይ የአንድ የመጨረሻ ተግባር ግምታዊ ምሳሌ።

አንዳንድ ጊዜ አንድ ተጨማሪ ተግባር ማጠናቀቅ ያስፈልግዎታል-

ቀኖናዊውን ማትሪክስ መበስበስን ይፃፉ

ምንድን ነው?

የማትሪክስ ኢጂንቬክተሮች ከፈጠሩ መሠረትከዚያም እንደሚከተለው ሊወከል ይችላል፡-

የ eigenvectors መጋጠሚያዎችን ያቀፈ ማትሪክስ የት አለ ፣ - ሰያፍማትሪክስ ከተዛማጅ ኢጂን እሴቶች ጋር።

ይህ ማትሪክስ መበስበስ ይባላል ቀኖናዊወይም ሰያፍ.

የመጀመሪያውን ምሳሌ ማትሪክስ እንመልከት. የእሱ ኢጂንቬክተሮች በመስመር ገለልተኛ(ከላይ ያልሆነ) እና መሠረት ይመሰርታሉ። የእነሱ መጋጠሚያዎች ማትሪክስ እንፍጠር፡-

በርቷል ዋና ሰያፍማትሪክስ በተገቢው ቅደም ተከተልየ eigenvalues ​​ይገኛሉ ፣ እና የተቀሩት ንጥረ ነገሮች ከዜሮ ጋር እኩል ናቸው።
- እንደገና የትዕዛዝ አስፈላጊነትን አፅንዖት እሰጣለሁ-"ሁለት" ከ 1 ኛ ቬክተር ጋር ይዛመዳል እና ስለዚህ በ 1 ኛ ረድፍ "ሶስት" - ወደ 2 ኛ ቬክተር ውስጥ ይገኛል.

ለማግኘት የተለመደውን ስልተ ቀመር በመጠቀም የተገላቢጦሽ ማትሪክስወይም የጋውስ-ዮርዳኖስ ዘዴእናገኛለን . አይ፣ ያ ፊደል አይደለም! - ከእርስዎ በፊት ያልተለመደ ክስተት ነው ፣ ልክ እንደ የፀሐይ ግርዶሽ ፣ ተቃራኒው ከመጀመሪያው ማትሪክስ ጋር ሲገጣጠም።

የማትሪክስ ቀኖናዊ መበስበስን ለመጻፍ ይቀራል፡-

ስርዓቱ የአንደኛ ደረጃ ለውጦችን በመጠቀም ሊፈታ ይችላል, እና በሚቀጥሉት ምሳሌዎች ወደዚህ ዘዴ እንጠቀማለን. ግን እዚህ "ትምህርት ቤት" ዘዴ በጣም በፍጥነት ይሰራል. ከ 3 ኛ እኩልታ እንገልፃለን - በሁለተኛው እኩልዮሽ መተካት

የመጀመሪያው መጋጠሚያ ዜሮ ስለሆነ, ስርዓትን እናገኛለን, ከእያንዳንዱ እኩልታ ይከተላል.

እና እንደገና የመስመር ግንኙነት የግዴታ መገኘት ትኩረት ይስጡ. ቀላል ያልሆነ መፍትሄ ብቻ ከተገኘ , ከዚያ ወይ eigenvalue በስህተት ተገኝቷል, ወይም ስርዓቱ ተሰብስቦ / በስህተት ተፈቷል.

የታመቁ መጋጠሚያዎች ዋጋውን ይሰጣሉ

ኢጂንቬክተር፡

እና አንድ ጊዜ, መፍትሄው እንደተገኘ እናረጋግጣለን የስርዓቱን እያንዳንዱን እኩልታ ያሟላል።. በቀጣዮቹ አንቀጾች እና በሚቀጥሉት ተግባራት, ይህንን ምኞት እንደ አስገዳጅ ህግ እንዲወስዱ እመክራለሁ.

2) ለ eigenvalue ፣ ተመሳሳይ መርህ በመጠቀም ፣ የሚከተለውን ስርዓት እናገኛለን

ከስርአቱ 2ኛ እኩልታ እንገልፃለን፡- በሦስተኛው እኩልታ መተካት፡-

የ "zeta" መጋጠሚያ ከዜሮ ጋር እኩል ስለሆነ, ከእያንዳንዱ እኩልታ መስመር ጥገኝነት የሚከተልበትን ስርዓት እናገኛለን.

ፍቀድ

መፍትሄውን በማጣራት ላይ የስርዓቱን እያንዳንዱን እኩልታ ያሟላል።

ስለዚህም ኢጂንቬክተሩ፡.

3) እና በመጨረሻም ስርዓቱ ከ eigenvalue ጋር ይዛመዳል-

ሁለተኛው እኩልታ በጣም ቀላሉን ነው የሚመስለው፣ ስለዚህ እንገልጠው እና በ 1 ኛ እና 3 ኛ እኩልታዎች እንተካው፡-

ሁሉም ነገር ጥሩ ነው - ቀጥተኛ ግንኙነት ተፈጥሯል ፣ እሱም ወደ አገላለጹ እንተካለን።

በውጤቱም፣ “x” እና “y” በ “z”፡ ተገልጸዋል። በተግባር, እንደዚህ አይነት ግንኙነቶችን በትክክል ማግኘት አስፈላጊ አይደለም, በአንዳንድ ሁኔታዎች በሁለቱም በኩል ወይም እና በ . ወይም እንዲያውም “ባቡር” - ለምሳሌ “X” በ “I” እና “I” በ “Z” በኩል

እንግዲህ እናስቀምጠው፡-

መፍትሄው እንደተገኘ እናረጋግጣለን። የስርዓቱን እያንዳንዱን እኩልታ ያሟላ እና ሶስተኛውን ኢጂንቬክተር ይጽፋል

መልስኢጂንቬክተሮች

በጂኦሜትሪ እነዚህ ቬክተሮች ሶስት የተለያዩ የቦታ አቅጣጫዎችን ይገልፃሉ። ("እዛ እና እንደገና ተመለስ"), በዚህ መሠረት መስመራዊ ለውጥዜሮ ያልሆኑ ቬክተሮችን (eigenvectors) ወደ ኮላይኔር ቬክተር ይለውጣል።

ቀኖናዊውን ብስባሽ መፈለግ የሚያስፈልገው ሁኔታ ከሆነ, ይህ እዚህ ይቻላል, ምክንያቱም የተለያዩ የ eigenvalues ​​ከተለያዩ ቀጥተኛ ገለልተኛ ኢጂንቬክተሮች ጋር ይዛመዳሉ። ማትሪክስ መስራት ከመጋጠሚያዎቻቸው, ሰያፍ ማትሪክስ ከ ተዛማጅ eigenvalues ​​እና ያግኙ የተገላቢጦሽ ማትሪክስ .

እንደ ሁኔታው ​​ከሆነ, መጻፍ ያስፈልግዎታል በ eigenvectors መሠረት ውስጥ መስመራዊ የለውጥ ማትሪክስ, ከዚያም መልሱን በቅጹ እንሰጣለን. ልዩነት አለ, እና ልዩነቱ ጉልህ ነው!ምክንያቱም ይህ ማትሪክስ "de" ማትሪክስ ነው.

በራስዎ የሚፈቱት ቀላል ስሌቶች ችግር፡-

ምሳሌ 5

በማትሪክስ የተሰጠውን የመስመር ለውጥ ኢጂንቬክተሮችን ያግኙ

የራስዎን ቁጥሮች ሲፈልጉ, ወደ 3 ኛ ዲግሪ ፖሊኖሚል ላለመሄድ ይሞክሩ. በተጨማሪም የስርዓትዎ መፍትሄዎች ከኔ መፍትሄዎች ሊለያዩ ይችላሉ - እዚህ ምንም እርግጠኛነት የለም; እና የሚያገኟቸው ቬክተሮች ከናሙና ቬክተሮች እስከ የየራሳቸው መጋጠሚያዎች ተመጣጣኝነት ሊለያዩ ይችላሉ. ለምሳሌ, እና. መልሱን በቅጹ ላይ ለማቅረብ የበለጠ ውበት ያለው ነው, ነገር ግን በሁለተኛው አማራጭ ላይ ካቆሙ ምንም አይደለም. ሆኖም ፣ ለሁሉም ነገር ምክንያታዊ ገደቦች አሉ ፣ ስሪቱ ከአሁን በኋላ በጣም ጥሩ አይመስልም።

በትምህርቱ መጨረሻ ላይ ያለው ግምታዊ የመጨረሻ ናሙና።

ችግሩን በበርካታ ኢጂኖች ጉዳይ እንዴት መፍታት ይቻላል?

አጠቃላይ ስልተ ቀመር ተመሳሳይ ነው, ነገር ግን የራሱ ባህሪያት አለው, እና የመፍትሄውን አንዳንድ ክፍሎች ይበልጥ ጥብቅ በሆነ የአካዳሚክ ዘይቤ ውስጥ ማስቀመጥ ይመከራል.

ምሳሌ 6

ኢጂንቫሉስ እና ኢጂንቬክተሮችን ያግኙ

መፍትሄ

በእርግጥ፣ አስደናቂውን የመጀመሪያውን ዓምድ በካፒታል እናድርገው፡-

እና ኳድራቲክ ትሪኖሚል ካደረጉ በኋላ፡-

በውጤቱም, eigenvalues ​​ተገኝተዋል, ሁለቱ ብዜቶች ናቸው.

ኢጂንቬክተሮችን እንፈልግ፡-

1) በብቸኛ ወታደር “በቀላል” እቅድ መሰረት እንገናኝ፡-

ከመጨረሻዎቹ ሁለት እኩልታዎች ፣ እኩልነት በግልፅ ይታያል ፣ እሱም በግልፅ ፣ በስርዓቱ 1 ኛ እኩልነት መተካት አለበት ።

የተሻለ ጥምረት አያገኙም፡-
ኢጂንቬክተር፡

2-3) አሁን ሁለት ሴንትሪዎችን እናስወግዳለን. በዚህ ሁኔታ ውስጥ ሊለወጥ ይችላል ወይ ሁለት ወይም አንድ eigenvector. የስርወቹ ብዛት ምንም ይሁን ምን እሴቱን ወደ ወሳኙ እንተካለን። ቀጣዩን ያመጣናል የመስመር እኩልታዎች ተመሳሳይ ስርዓት:

Eigenvectors በትክክል ቬክተር ናቸው
መሠረታዊ የመፍትሄዎች ስርዓት

በእውነቱ፣ በጠቅላላው ትምህርት የመሠረታዊ ስርዓቱን አካላት ከማግኘት በቀር ምንም አላደረግንም። ለጊዜው ይህ ቃል በተለይ አያስፈልግም ነበር. በነገራችን ላይ ርዕሱን በካሜራ ልብስ ለብሰው ያመለጡት ጎበዝ ተማሪዎች ተመሳሳይነት ያላቸው እኩልታዎች, አሁን ለማጨስ ይገደዳል.

ብቸኛው እርምጃ ተጨማሪ መስመሮችን ማስወገድ ነበር. ውጤቱም በመሃል ላይ መደበኛ "ደረጃ" ያለው አንድ-በ-ሶስት ማትሪክስ ነው.
- መሠረታዊ ተለዋዋጭ, - ነፃ ተለዋዋጮች. ሁለት ነጻ ተለዋዋጮች አሉ, ስለዚህ የመሠረታዊ ሥርዓት ሁለት ቬክተሮችም አሉ.

መሠረታዊውን ተለዋዋጭ በነፃ ተለዋዋጮች እንግለጽ፡. በ "X" ፊት ያለው ዜሮ ማባዛት ማንኛውንም እሴቶችን እንዲወስድ ያስችለዋል (ይህም ከእኩልታዎች ስርዓት በግልጽ ይታያል).

በዚህ ችግር አውድ ውስጥ አጠቃላይ መፍትሄን በተከታታይ ሳይሆን በአምድ ውስጥ ለመፃፍ የበለጠ ምቹ ነው-

ጥንዶቹ ከኢጂንቬክተር ጋር ይዛመዳሉ፡-
ጥንዶቹ ከኢጂንቬክተር ጋር ይዛመዳሉ፡-

ማስታወሻ የተራቀቁ አንባቢዎች እነዚህን ቬክተሮች በቃል መምረጥ ይችላሉ - በቀላሉ ስርዓቱን በመተንተን , ግን እዚህ አንዳንድ እውቀት ያስፈልጋል: ሦስት ተለዋዋጮች አሉ, የስርዓት ማትሪክስ ደረጃ- አንድ, ማለትም መሠረታዊ ውሳኔ ሥርዓት 3 - 1 = 2 ቬክተሮችን ያካትታል. ነገር ግን፣ የተገኙት ቬክተሮች ያለዚህ እውቀት እንኳን በግልጽ የሚታዩ ናቸው፣ በማስተዋል ደረጃ ብቻ። በዚህ ሁኔታ, ሦስተኛው ቬክተር የበለጠ "በሚያምር" ይፃፋል. ሆኖም ግን, በሌላ ምሳሌ, ቀላል ምርጫ የማይቻል ሊሆን እንደሚችል አስጠነቅቃችኋለሁ, ለዚህም ነው አንቀጹ ልምድ ላላቸው ሰዎች የታሰበ ነው. በተጨማሪም, ለምን እንደ ሦስተኛው ቬክተር አትወስዱም? ከሁሉም በኋላ, የእሱ መጋጠሚያዎች የስርዓቱን እያንዳንዱን እኩልታ, እና ቬክተሮችን ያሟላሉ በመስመር ገለልተኛ። ይህ አማራጭ በመርህ ደረጃ ተስማሚ ነው ፣ ግን “የተጣመመ” ነው ፣ ምክንያቱም “ሌላው” ቬክተር የመሠረታዊ ስርዓቱ የቪክተሮች መስመራዊ ጥምረት ነው።

መልስኢጂንቫሉስ:, eigenvectors:

ለገለልተኛ መፍትሄ ተመሳሳይ ምሳሌ

ምሳሌ 7

ኢጂንቫሉስ እና ኢጂንቬክተሮችን ያግኙ

በትምህርቱ መጨረሻ ላይ የመጨረሻው ንድፍ ግምታዊ ናሙና.

በሁለቱም በ 6 ኛ እና 7 ኛ ምሳሌዎች ውስጥ ሶስት እጥፍ የመስመር ላይ ገለልተኛ eigenvectors መገኘቱን ልብ ሊባል ይገባል ፣ ስለሆነም ዋናው ማትሪክስ በቀኖናዊ መበስበስ ውስጥ ይወከላል ። ግን እንደዚህ ያሉ እንጆሪዎች በሁሉም ሁኔታዎች አይከሰቱም-

ምሳሌ 8

መፍትሄየባህሪውን እኩልታ እንፍጠር እና እንፍታ

በመጀመሪያው አምድ ውስጥ ወሳኙን እናስፋፋው፡-

ከሦስተኛ-ዲግሪ ፖሊኖሚል በማስቀረት በታሰበው ዘዴ መሠረት ተጨማሪ ማቃለያዎችን እናከናውናለን-

- ኢጂን እሴቶች.

ኢጂንቬክተሮችን እንፈልግ፡-

1) ከሥሩ ጋር ምንም ችግሮች የሉም:

አትደነቁ, ከመሳሪያው በተጨማሪ, ጥቅም ላይ የዋሉ ተለዋዋጮችም አሉ - እዚህ ምንም ልዩነት የለም.

ከ 3 ኛ እኩልታ እንገልፃለን እና በ 1 ኛ እና 2 ኛ እኩልታዎች እንተካለን ።

ከሁለቱም እኩልታዎች እንደሚከተለው ነው፡-

እንግዲህ፡-

2-3) ለብዙ እሴቶች ስርዓቱን እናገኛለን .

የስርአቱን ማትሪክስ እንፃፍ እና የመጀመሪያ ደረጃ ለውጦችን በመጠቀም ወደ ደረጃ አቅጣጫ አምጣው።

www.ጣቢያእንድታገኝ ይፈቅድልሃል . ጣቢያው ስሌቱን ያከናውናል. በጥቂት ሰከንዶች ውስጥ አገልጋዩ ትክክለኛውን መፍትሄ ይሰጣል. ለማትሪክስ የባህሪ እኩልታወሳኙን ለማስላት ደንቡን በመጠቀም የተገኘ የአልጀብራ አገላለጽ ይሆናል። ማትሪክስ ማትሪክስበዋናው ዲያግናል በኩል በሰያፍ አካላት እና በተለዋዋጭ እሴቶች ላይ ልዩነቶች ይኖራሉ። በማስላት ጊዜ በመስመር ላይ ለማትሪክስ የባህሪ እኩልታ, እያንዳንዱ ንጥረ ነገር ማትሪክስከሌሎች ተጓዳኝ አካላት ጋር ይባዛሉ ማትሪክስ. ሞድ ውስጥ አግኝ መስመር ላይለካሬ ብቻ ይቻላል ማትሪክስ. ክወና ማግኘት በመስመር ላይ ለማትሪክስ የባህሪ እኩልታየንጥረ ነገሮች ምርት የአልጀብራ ድምርን ለማስላት ይቀንሳል ማትሪክስየሚወስነውን በማግኘት ምክንያት ማትሪክስ, ለመወሰን ዓላማ ብቻ በመስመር ላይ ለማትሪክስ የባህሪ እኩልታ. ይህ ክዋኔ በንድፈ ሀሳብ ውስጥ ልዩ ቦታ ይይዛል ማትሪክስ, ሥሮችን በመጠቀም eigenvalues ​​እና vectors እንዲያገኙ ያስችልዎታል. የማግኘት ተግባር በመስመር ላይ ለማትሪክስ የባህሪ እኩልታየሚባዙ ንጥረ ነገሮችን ያካትታል ማትሪክስእነዚህን ምርቶች በተወሰነ ደንብ መሰረት በማጠቃለል. www.ጣቢያያገኛል ለማትሪክስ የባህሪ እኩልታበሁኔታ የተሰጠው ልኬት መስመር ላይ. ስሌት በመስመር ላይ ለማትሪክስ የባህሪ እኩልታከስፋቱ አንፃር፣ ይህ ወሳኙን ለማስላት በደንቡ መሠረት የሚገኘውን የቁጥር ወይም ምሳሌያዊ ጥምርታ ያለው ፖሊኖሚል ማግኘት ነው። ማትሪክስ- እንደ ተጓዳኝ አካላት ምርቶች ድምር ማትሪክስ, ለመወሰን ዓላማ ብቻ በመስመር ላይ ለማትሪክስ የባህሪ እኩልታ. ለኳድራቲክ ከተለዋዋጭ አንፃር ፖሊኖሚል ማግኘት ማትሪክስ, እንደ ፍቺ ለማትሪክስ የባህሪ እኩልታ, በንድፈ ሀሳብ የተለመደ ማትሪክስ. የአንድ ፖሊኖሚል ሥሮች ትርጉም በመስመር ላይ ለማትሪክስ የባህሪ እኩልታ eigenvectors እና eigenvalues ​​ለ ለመወሰን ጥቅም ላይ ይውላል ማትሪክስ. ከዚህም በላይ የሚወስነው ከሆነ ማትሪክስከዜሮ ጋር እኩል ይሆናል, ከዚያ የማትሪክስ ባህሪ እኩልታአሁንም ይኖራል, በተቃራኒው በተቃራኒው ማትሪክስ. ለማስላት ለማትሪክስ የባህሪ እኩልታወይም ለብዙዎች በአንድ ጊዜ ይፈልጉ ማትሪክስ የባህሪ እኩልታዎች, ብዙ ጊዜ እና ጥረት ማሳለፍ አለቦት, የእኛ አገልጋይ ግን በሰከንዶች ጊዜ ውስጥ ያገኛል በመስመር ላይ ለማትሪክስ የባህሪ እኩልታ. በዚህ ጉዳይ ላይ, ለማግኘት መልስ በመስመር ላይ ለማትሪክስ የባህሪ እኩልታምንም እንኳን ቁጥሮቹ ሲገኙ ምንም እንኳን ትክክለኛ እና በቂ ትክክለኛነት ይኖራቸዋል በመስመር ላይ ለማትሪክስ የባህሪ እኩልታምክንያታዊነት የጎደለው ይሆናል. በጣቢያው ላይ www.ጣቢያየቁምፊ ግቤቶች በንጥረ ነገሮች ውስጥ ይፈቀዳሉ ማትሪክስ, ያውና በመስመር ላይ ለማትሪክስ የባህሪ እኩልታበማስላት ጊዜ በአጠቃላይ ምሳሌያዊ መልክ ሊወከል ይችላል በመስመር ላይ የማትሪክስ ባህሪ እኩልታ. የማግኘት ችግርን በሚፈታበት ጊዜ የተገኘውን መልስ መፈተሽ ጠቃሚ ነው በመስመር ላይ ለማትሪክስ የባህሪ እኩልታጣቢያውን በመጠቀም www.ጣቢያ. ፖሊኖሚል የማስላት ሥራ ሲያከናውን - የማትሪክስ ባህሪ እኩልታ, ይህንን ችግር በሚፈታበት ጊዜ ጥንቃቄ እና ከፍተኛ ትኩረት መስጠት አለብዎት. በምላሹ, የእኛ ጣቢያ በርዕሱ ላይ የእርስዎን ውሳኔ እንዲፈትሹ ይረዳዎታል በመስመር ላይ የማትሪክስ ባህሪ እኩልታ. ለተፈቱ ችግሮች ረጅም ቼኮች ጊዜ ከሌለዎት, ከዚያ www.ጣቢያበእርግጥ ሲፈልጉ እና ሲሰላ ለመፈተሽ ምቹ መሳሪያ ይሆናል። በመስመር ላይ ለማትሪክስ የባህሪ እኩልታ.

የአንድ ካሬ ማትሪክስ ኢጂንቬክተር በተሰጠው ማትሪክስ ሲባዛ ኮሊንየር ቬክተርን የሚያመጣ ነው። በቀላል አነጋገር ፣ ማትሪክስ በ eigenvector ሲባዛ ፣ የኋለኛው ተመሳሳይ ነው ፣ ግን በተወሰነ ቁጥር ተባዝቷል።

ፍቺ

eigenvector ዜሮ ያልሆነ ቬክተር V ነው፣ እሱም በካሬ ማትሪክስ M ሲባዛ፣ ራሱ በተወሰነ ቁጥር λ ይጨምራል። በአልጀብራ አጻጻፍ የሚከተለውን ይመስላል።

M × V = λ × V፣

የት λ የማትሪክስ M eigenvalue ነው።

የቁጥር ምሳሌን እንመልከት። ለመቅዳት ቀላልነት፣ በማትሪክስ ውስጥ ያሉት ቁጥሮች በሰሚኮሎን ይለያያሉ። ማትሪክስ ይኑረን፡-

• M = 0; 4;
• 6; 10.

በአምድ ቬክተር እናባዛው፡-

• ቪ = -2;

ማትሪክስ በአምድ ቬክተር ስናባዛው ደግሞ የአምድ ቬክተር እናገኛለን። በጥብቅ የሒሳብ ቋንቋ 2 × 2 ማትሪክስ በአምድ ቬክተር የማባዛት ቀመር ይህን ይመስላል።

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 ማለት በመጀመሪያው ረድፍ እና በመጀመሪያው አምድ ውስጥ የሚገኘው የማትሪክስ M አባል ሲሆን M22 ማለት ደግሞ በሁለተኛው ረድፍ እና በሁለተኛው ረድፍ ውስጥ የሚገኝ አካል ማለት ነው. ለኛ ማትሪክስ እነዚህ ንጥረ ነገሮች ከ M11 = 0, M12 = 4, M21 = 6, M22 10 ጋር እኩል ናቸው. ለአንድ አምድ ቬክተር, እነዚህ እሴቶች ከ V11 = -2, V21 = 1 ጋር እኩል ናቸው. በዚህ ቀመር መሠረት. የሚከተለውን የካሬ ማትሪክስ ውጤት በቬክተር እናገኛለን።

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

ለመመቻቸት የዓምድ ቬክተርን በአንድ ረድፍ እንፃፍ። ስለዚህ, ካሬውን ማትሪክስ በቬክተር (-2; 1) እናባዛለን, በዚህም ምክንያት ቬክተር (4; -2). በግልጽ ለማየት እንደሚቻለው, ይህ በ λ = -2 ተባዝቶ ተመሳሳይ ቬክተር ነው. Lambda በዚህ ጉዳይ ላይ የማትሪክስ ኢጂን ዋጋን ያመለክታል.

የማትሪክስ ኢጂንቬክተር ኮላይኔር ቬክተር ነው፣ ማለትም፣ በማትሪክስ ሲባዛ ቦታውን በህዋ ላይ የማይለውጥ ነገር ነው። በቬክተር አልጀብራ ውስጥ ያለው የኮላይኔሪቲ ጽንሰ-ሐሳብ በጂኦሜትሪ ውስጥ ካለው ትይዩነት ቃል ጋር ተመሳሳይ ነው። በጂኦሜትሪክ አተረጓጎም, ኮላይኔር ቬክተሮች የተለያየ ርዝመት ያላቸው ትይዩ የተመሩ ክፍሎች ናቸው. ከዩክሊድ ዘመን ጀምሮ፣ አንድ መስመር ከሱ ጋር ትይዩ የሆኑ ማለቂያ የሌላቸው መስመሮች እንዳሉት እናውቃለን፣ ስለዚህ እያንዳንዱ ማትሪክስ ማለቂያ የሌለው የኢጂንቬክተሮች ብዛት አለው ብሎ ማሰብ ምክንያታዊ ነው።

ካለፈው ምሳሌ ግልጽ የሆነው ኢጂንቬክተሮች (-8; 4) እና (16; -8) እና (32, -16) ሊሆኑ ይችላሉ. እነዚህ ሁሉ ከ eigenvalue λ = -2 ጋር የሚዛመዱ ኮላይኔር ቬክተሮች ናቸው። ዋናውን ማትሪክስ በእነዚህ ቬክተሮች ስናባዛው አሁንም ከዋናው በ2 ጊዜ የሚለይ ቬክተር ይዘን እንጨርሳለን። ለዚህም ነው ኢጂንቬክተርን የማግኘት ችግሮችን በሚፈታበት ጊዜ, በመስመር ላይ ገለልተኛ የሆኑ የቬክተር እቃዎችን ብቻ ማግኘት አስፈላጊ ነው. ብዙ ጊዜ፣ ለ n × n ማትሪክስ፣ n የ eigenvectors ብዛት አለ። የእኛ ካልኩሌተር ሁለተኛ ደረጃ ካሬ ማትሪክስ ለመተንተን የተነደፈ ነው, ስለዚህ ሁልጊዜ ማለት ይቻላል ውጤቱ ሁለት eigenvectors ታገኛላችሁ, ከተጋጠሙትም ሁኔታዎች በስተቀር.

ከላይ ባለው ምሳሌ የዋናውን ማትሪክስ ኢጂንቬክተር አስቀድመን አውቀናል እና የላምዳ ቁጥርን በግልፅ ወስነናል። ሆኖም ግን, በተግባር, ሁሉም ነገር በተቃራኒው ይከናወናል-የኢጂነን እሴቶቹ መጀመሪያ የተገኙት እና ከዚያ በኋላ ብቻ ናቸው.

የመፍትሄው ስልተ ቀመር

ዋናውን ማትሪክስ M እንደገና እንመልከተው እና ሁለቱንም ኢጂንቬክተሮች ለማግኘት እንሞክር። ስለዚህ ማትሪክስ የሚከተለው ይመስላል-

• M = 0; 4;
• 6; 10.

በመጀመሪያ የሚከተለውን ማትሪክስ ወሳኙን ማስላት የሚጠይቀውን eigenvalue λ መወሰን አለብን።

• (0 - λ); 4;
• 6; (10 - λ).

ይህ ማትሪክስ የሚገኘው የማይታወቅ λን ከዋናው ዲያግናል ላይ ካሉ ንጥረ ነገሮች በመቀነስ ነው። የሚወስነው መደበኛውን ቀመር በመጠቀም ነው፡-

• detA = M11 × M21 - M12 × M22
• detA = (0 - λ) × (10 - λ) - 24

የእኛ ቬክተር ዜሮ ያልሆነ መሆን ስላለበት፣ የተገኘውን እኩልታ እንደ መስመራዊ ጥገኛ አድርገን ተቀብለን ወሳኙን detAን ከዜሮ ጋር እናነፃፅራለን።

(0 - λ) × (10 - λ) - 24 = 0

ቅንፎችን እንከፍት እና የማትሪክስ ባህሪ እኩልታ እናገኛለን፡-

λ 2 - 10λ - 24 = 0

ይህ አድሎአዊ በመጠቀም መፍታት ያለበት መደበኛ ኳድራቲክ እኩልታ ነው።

D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

የአድሎአዊው ሥር sqrt (D) = 14 ነው, ስለዚህ λ1 = -2, λ2 = 12. አሁን ለእያንዳንዱ ላምዳ እሴት ኢጂንቬክተሩን መፈለግ አለብን. ለ λ = -2 የስርዓት ቅንጅቶችን እንገልፃለን.

• M - λ × E = 2; 4;
• 6; 12.

በዚህ ቀመር ኢ የማንነት ማትሪክስ ነው። በውጤቱ ማትሪክስ ላይ በመመስረት ፣ የመስመሮች እኩልታዎች ስርዓት እንፈጥራለን-

2x + 4y = 6x + 12y፣

x እና y የኢጂንቬክተር አካላት ሲሆኑ።

ሁሉንም X በስተግራ እና ሁሉንም Y በስተቀኝ እንሰበስብ። በግልጽ - 4x = 8y. አገላለጹን በ - 4 ይከፋፍሉት እና x = -2y ያግኙ። አሁን የማንኛውንም የማይታወቁ እሴቶችን በመውሰድ የማትሪክስ የመጀመሪያውን eigenvector መወሰን እንችላለን (የመስመራዊ ጥገኛ ኢጂንቬክተሮች ወሰን አልባነት ያስታውሱ)። y = 1፣ በመቀጠል x = –2 እንውሰድ። ስለዚህ, የመጀመሪያው eigenvector V1 = (-2; 1) ይመስላል. ወደ መጣጥፉ መጀመሪያ ተመለስ። የኢጂንቬክተር ጽንሰ-ሀሳብን ለማሳየት ማትሪክስን ያባዛነው ይህ የቬክተር ነገር ነው።

አሁን eigenvector ለ λ = 12 እንፈልግ።

• M - λ × E = -12; 4
• 6; -2.

የመስመር እኩልታዎች ተመሳሳይ ስርዓት እንፍጠር;

• -12x + 4y = 6x - 2y
• -18x = -6ይ
• 3x = y.

አሁን x = 1 ን እንወስዳለን, ስለዚህ y = 3. ስለዚህ, ሁለተኛው eigenvector V2 = (1; 3) ይመስላል. ዋናውን ማትሪክስ በተሰጠው ቬክተር ሲያባዙ ውጤቱ ሁሌም ተመሳሳይ ቬክተር በ 12 ተባዝቷል. ይህ የመፍትሄው አልጎሪዝም የሚያበቃበት ነው. አሁን የማትሪክስ ኢጂንቬክተርን እራስዎ እንዴት እንደሚወስኑ ያውቃሉ።

• የሚወስን;
• ፈለግ ፣ ማለትም ፣ በዋናው ዲያግናል ላይ ያሉት ንጥረ ነገሮች ድምር;
• ደረጃ፣ ማለትም፣ ከፍተኛው በመስመር ነጻ የሆኑ ረድፎች/አምዶች ብዛት።

መርሃግብሩ ከላይ በተጠቀሰው ስልተ-ቀመር መሰረት ይሰራል, በተቻለ መጠን የመፍትሄ ሂደቱን ያሳጥራል. በፕሮግራሙ ውስጥ ላምዳ በ "ሐ" ፊደል እንደተሰየመ ማመላከት አስፈላጊ ነው. የቁጥር ምሳሌን እንመልከት።

ፕሮግራሙ እንዴት እንደሚሰራ የሚያሳይ ምሳሌ

ለሚከተለው ማትሪክስ ኢጂንቬክተሮችን ለመወሰን እንሞክር፡-

• M = 5; 13;
• 4; 14.

እነዚህን እሴቶች ወደ ካልኩሌተሩ ህዋሶች እናስገባና መልሱን በሚከተለው መልክ እናገኝ።

• ማትሪክስ ደረጃ፡ 2;
• ማትሪክስ መወሰኛ: 18;
• ማትሪክስ ዱካ: 19;
• የ eigenvector ስሌት: c 2 - 19.00c + 18.00 (የባህሪ እኩልነት);
• Eigenvector ስሌት: 18 (የመጀመሪያው ላምዳ ዋጋ);
• Eigenvector ስሌት: 1 (ሁለተኛ ላምዳ ዋጋ);
• የእኩልታዎች ስርዓት ለቬክተር 1: -13x1 + 13y1 = 4x1 - 4y1;
• ለቬክተር 2 የእኩልታዎች ስርዓት: 4x1 + 13y1 = 4x1 + 13y1;
• ኢጅንቬክተር 1: (1; 1);
• ኢጅንቬክተር 2፡ (-3.25፤ 1)።

ስለዚህም ሁለት ቀጥተኛ ገለልተኛ ኢጂንቬክተሮች አግኝተናል።

ማጠቃለያ

የመስመር አልጀብራ እና የትንታኔ ጂኦሜትሪ ለማንኛውም የአንደኛ ደረጃ ምህንድስና ተማሪ መደበኛ የትምህርት ዓይነቶች ናቸው። ብዛት ያላቸው ቬክተሮች እና ማትሪክስ በጣም አስፈሪ ናቸው, እና እንደዚህ ባሉ አስቸጋሪ ስሌቶች ውስጥ ስህተቶችን ማድረግ ቀላል ነው. የእኛ ፕሮግራም ተማሪዎች ስሌቶቻቸውን እንዲፈትሹ ወይም ኢጂንቬክተር የማግኘት ችግርን በራስ-ሰር እንዲፈቱ ያስችላቸዋል። በእኛ ካታሎግ ውስጥ ሌሎች የመስመር አልጀብራ አስሊዎች አሉ፤ በጥናትዎ ወይም በስራዎ ውስጥ ይጠቀሙባቸው።

"የመጀመሪያው ክፍል ኬሞሜትሮችን ለመገንዘብ በትንሹ አስፈላጊ የሆኑትን ድንጋጌዎች ያዘጋጃል, ሁለተኛው ክፍል ደግሞ የባለብዙ ልዩነት ትንተና ዘዴዎችን በጥልቀት ለመረዳት ማወቅ ያለብዎትን እውነታዎች ይዟል. አቀራረቡ በኤክሴል የስራ ደብተር ውስጥ በተዘጋጁ ምሳሌዎች ተብራርቷል. ማትሪክስ.xls, ከዚህ ሰነድ ጋር አብሮ የሚሄድ.

የምሳሌዎች አገናኞች በጽሁፉ ውስጥ እንደ ኤክሴል ነገሮች ተቀምጠዋል። እነዚህ ምሳሌዎች ረቂቅ ተፈጥሮ ናቸው፤ እነሱ በምንም መልኩ ከትንታኔ ኬሚስትሪ ችግሮች ጋር የተሳሰሩ አይደሉም። በኬሞሜትሪ ውስጥ የማትሪክስ አልጀብራ አጠቃቀምን የሚያሳዩ የእውነተኛ ህይወት ምሳሌዎች በሌሎች የተለያዩ የኬሞሜትሪክ አፕሊኬሽኖች በሚሸፍኑ ጽሑፎች ላይ ተብራርተዋል።

በአናቲቲካል ኬሚስትሪ ውስጥ የተደረጉ አብዛኛዎቹ መለኪያዎች ቀጥተኛ አይደሉም፣ ግን ቀጥተኛ ያልሆነ. ይህ ማለት በሙከራው ውስጥ, ከተፈለገው ትንተና C (ማጎሪያ) ዋጋ ይልቅ ሌላ እሴት ተገኝቷል x(ምልክት)፣ ተዛማጅ ግን ከ C ጋር እኩል ያልሆነ፣ ማለትም x(ሐ) ≠ C. እንደ ደንቡ, የጥገኛ ዓይነት x(ሐ) የማይታወቅ ነው፣ ግን እንደ እድል ሆኖ በትንታኔ ኬሚስትሪ አብዛኞቹ ልኬቶች ተመጣጣኝ ናቸው። ይህ ማለት በሲ ውስጥ እየጨመረ በሄደ መጠን ሀጊዜ፣ ሲግናል X በተመሳሳይ መጠን ይጨምራል፣ ማለትም። x(ሀሐ) = አንድ x(ሐ) በተጨማሪም ምልክቶቹም ተጨማሪዎች ናቸው, ስለዚህ ሁለት ንጥረ ነገሮች C 1 እና C 2 ያላቸው ንጥረ ነገሮች የሚገኙበት የናሙና ምልክት ከእያንዳንዱ ክፍል ምልክቶች ድምር ጋር እኩል ይሆናል, ማለትም. x(C 1 + C 2) = x(ሲ 1)+ x(ሐ 2) ተመጣጣኝነት እና መደመር አንድ ላይ ይሰጣሉ መስመራዊነት. የመስመራዊነት መርህን ለማሳየት ብዙ ምሳሌዎችን መስጠት ይቻላል ነገርግን ሁለቱን በጣም አስደናቂ ምሳሌዎችን መጥቀስ በቂ ነው - ክሮሞግራፊ እና ስፔክትሮስኮፒ። በመተንተን ኬሚስትሪ ውስጥ በሙከራ ውስጥ ያለው ሁለተኛው ባህሪ ነው። ባለብዙ ቻናል. ዘመናዊ የትንታኔ መሳሪያዎች ለብዙ ቻናሎች ምልክቶችን በአንድ ጊዜ ይለካሉ. ለምሳሌ, የብርሃን ማስተላለፊያው ጥንካሬ በአንድ ጊዜ ለብዙ የሞገድ ርዝመቶች ይለካል, ማለትም. ክልል. ስለዚህ, በሙከራው ውስጥ ከብዙ ምልክቶች ጋር እንገናኛለን x 1 , x 2 ,...., x n, በጥናት ላይ ባለው ስርዓት ውስጥ የሚገኙትን የስብስብ ስብስቦችን መለየት C 1, C 2, ..., C m.

ሩዝ. 1 Spectra

ስለዚህ፣ የትንታኔ ሙከራ በመስመራዊነት እና ባለብዙ ገፅታነት ይገለጻል። ስለዚህ የሙከራ መረጃዎችን እንደ ቬክተር እና ማትሪክስ በመቁጠር የማትሪክስ አልጀብራን በመጠቀም እነሱን ለመጠቀም ምቹ ነው። የዚህ አካሄድ ፍሬያማነት በምሳሌነት የሚገለፀው በ 200 የሞገድ ርዝመት ከ 4000 እስከ 4796 ሴ.ሜ -1 የተወሰዱ ሶስት ስፔክተሮችን ያሳያል ። አንደኛ ( x 1) እና ሁለተኛ ( x 2) ስፔክተሩ የተገኘው ለመደበኛ ናሙናዎች ሲሆን ይህም የሁለት ንጥረ ነገሮች A እና B መጠን የሚታወቅ ሲሆን በመጀመሪያው ናሙና [A] = 0.5, [B] = 0.1, እና በሁለተኛው ናሙና [A] = 0.2, [ B] = 0.6. ስለ አዲስ የማይታወቅ ናሙና ምን ማለት ይቻላል, ስፔክትረም ይጠቁማል x 3 ?

እስቲ ሦስት የሙከራ ማሳያዎችን እንመልከት x 1 , x 2 እና x 3 እንደ ሶስት ቬክተሮች ልኬት 200. ሊኒያር አልጀብራን በመጠቀም በቀላሉ ያንን ያሳያል x 3 = 0.1 x 1 +0.3 x 2, ስለዚህ ሦስተኛው ናሙና በግልጽ A እና B ንጥረ ነገሮች ብቻ ይዟል [A] = 0.5×0.1 + 0.2×0.3 = 0.11 እና [B] = 0.1×0.1 + 0.6×0.3 = 0.19.

1. መሰረታዊ መረጃ

1.1 ማትሪክስ

ማትሪክስለምሳሌ አራት ማዕዘን ቅርጽ ያለው የቁጥሮች ሰንጠረዥ ይባላል

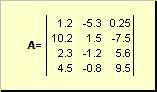
ሩዝ. 2 ማትሪክስ

ማትሪክስ በትልቅ ደፋር ፊደላት ይወከላል ( ሀ), እና አካሎቻቸው - ከትንሽ ሆሄያት ጋር በተዛመደ ኢንዴክሶች, ማለትም. ሀ ij. የመጀመሪያው መረጃ ጠቋሚ ረድፎችን, እና ሁለተኛው - አምዶች. በኬሞሜትሪክስ ውስጥ የአንድ ኢንዴክስ ከፍተኛውን እሴት ልክ እንደ ኢንዴክስ በራሱ ተመሳሳይ ፊደል ማመልከት የተለመደ ነው, ነገር ግን በካፒታል ፊደላት. ስለዚህ ማትሪክስ ሀእንዲሁም እንደሚከተለው ሊፃፍ ይችላል ሀ ij , እኔ = 1,..., አይ; ጄ = 1,..., ጄ). ለምሳሌ ማትሪክስ አይ = 4, ጄ= 3 እና ሀ 23 = −7.5.

የቁጥሮች ጥንድ አይእና ጄየማትሪክስ ልኬት ተብሎ ይጠራል እና እንደ ተጠቁሟል አይ× ጄ. በኬሞሜትሪ ውስጥ የማትሪክስ ምሳሌ የተገኘ የእይታ ስብስብ ነው። አይናሙናዎች ለ ጄየሞገድ ርዝመቶች.

1.2. በጣም ቀላሉ ኦፕሬሽኖች ከማትሪክስ ጋር

ማትሪክስ ሊሆን ይችላል በቁጥር ማባዛት።. በዚህ ሁኔታ, እያንዳንዱ ንጥረ ነገር በዚህ ቁጥር ተባዝቷል. ለምሳሌ -

ሩዝ. 3 ማትሪክስ በቁጥር ማባዛት።

ተመሳሳይ መጠን ያላቸው ሁለት ማትሪክስ ንጥረ ነገሮች በንጥረ ነገር ሊሆኑ ይችላሉ። ማጠፍእና መቀነስ. ለምሳሌ,

ሩዝ. 4 ማትሪክስ መጨመር

በቁጥር እና በመደመር ማባዛት ምክንያት, ተመሳሳይ መጠን ያለው ማትሪክስ ተገኝቷል.

ዜሮ ማትሪክስ ዜሮዎችን ያካተተ ማትሪክስ ነው። የተሰየመ ነው። ኦ. እንደሆነ ግልጽ ነው። ሀ+ኦ = ሀ, ሀ−ሀ = ኦእና 0 ሀ = ኦ.

ማትሪክስ ሊሆን ይችላል ማስተላለፍ. በዚህ ቀዶ ጥገና ወቅት, ማትሪክስ ይገለበጣል, ማለትም. ረድፎች እና ዓምዶች ተለዋወጡ። ሽግግር በዋና ይገለጻል ፣ ሀ"ወይም ኢንዴክስ ሀቲ. ስለዚህ, ከሆነ ሀ = {ሀ ij , እኔ = 1,..., አይ; ጄ = 1,...,ጄ) ፣ ያ ሀቲ = ( ሀ ጂ , ጄ = 1,...,ጄ; እኔ = 1,..., አይ). ለምሳሌ

ሩዝ. 5 ማትሪክስ ሽግግር

ግልጽ ነው ( ሀ t) t = ሀ, (ሀ+ለ) ቲ =አ t+ ለቲ.

1.3. ማትሪክስ ማባዛት።

ማትሪክስ ሊሆን ይችላል ማባዛት, ግን ተገቢ ልኬቶች ካላቸው ብቻ ነው. ይህ የሆነው ለምን እንደሆነ ከትርጉሙ ግልጽ ይሆናል. የማትሪክስ ምርት ሀ፣ ልኬት አይ× ኬ, እና ማትሪክስ ለ፣ ልኬት ኬ× ጄ, ማትሪክስ ይባላል ሲ፣ ልኬት አይ× ጄ, የማን ንጥረ ነገሮች ቁጥሮች ናቸው

ስለዚህ ለምርቱ ABበግራ ማትሪክስ ውስጥ ያሉት የአምዶች ብዛት አስፈላጊ ነው ሀበቀኝ ማትሪክስ ውስጥ ካሉት የረድፎች ብዛት ጋር እኩል ነበር። ለ. የማትሪክስ ምርት ምሳሌ-

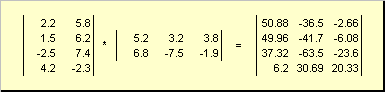
ምስል 6 የማትሪክስ ምርት

የማትሪክስ ማባዛት ደንብ እንደሚከተለው ሊቀረጽ ይችላል. የማትሪክስ አካል ለማግኘት ሲ, በመስቀለኛ መንገድ ላይ ቆሞ እኔ- ኛ መስመር እና ጄኛ አምድ ( ሐ ij) ኤለመንቱን በኤለመንት ማባዛት አለበት። እኔ- የመጀመሪያው ማትሪክስ ኛ ረድፍ ሀላይ ጄየሁለተኛው ማትሪክስ ኛ አምድ ለእና ሁሉንም ውጤቶች ይጨምሩ. ስለዚህ በምሳሌው ላይ ከሦስተኛው ረድፍ እና ከሁለተኛው ዓምድ አንድ ኤለመንት የሚገኘው የሶስተኛው ረድፍ ንጥረ-ጥበብ ምርቶች ድምር ነው. ሀእና ሁለተኛ ዓምድ ለ

ምስል 7 የማትሪክስ ምርት አካል

የማትሪክስ ምርት በትእዛዙ ላይ የተመሰረተ ነው, ማለትም. AB ≠ ቢ.ኤ.ቢያንስ በመጠን ምክንያቶች። ተላላኪ አይደለም ይላሉ። ይሁን እንጂ የማትሪክስ ምርት ተባባሪ ነው. ማለት ነው። ኢቢሲ = (AB)ሲ = ሀ(B.C.). በተጨማሪም, እሱ እንዲሁ አከፋፋይ ነው, ማለትም. ሀ(ለ+ሲ) = AB+አ.ሲ.. እንደሆነ ግልጽ ነው። አ.ኦ. = ኦ.

1.4. ካሬ ማትሪክስ

የማትሪክስ ዓምዶች ቁጥር ከረድፎቹ ቁጥር ጋር እኩል ከሆነ ( አይ = ጄ = ኤን), ከዚያ እንዲህ ዓይነቱ ማትሪክስ ካሬ ይባላል. በዚህ ክፍል ውስጥ እንደዚህ ያሉ ማትሪክቶችን ብቻ እንመለከታለን. ከእነዚህ ማትሪክስ መካከል ልዩ ባህሪያት ያላቸው ማትሪክስ መለየት ይቻላል.

ነጠላማትሪክስ (ተመስሏል እኔ፣እና አንዳንድ ጊዜ ኢ) ሁሉም ንጥረ ነገሮች ከዜሮ ጋር እኩል የሆኑበት ማትሪክስ ነው, ከዲያግኖል በስተቀር, ከ 1 ጋር እኩል ናቸው, ማለትም.

ግልጽ ነው። አ.አይ. = አይ.ኤ. = ሀ.

ማትሪክስ ይባላል ሰያፍሰያፍ ካልሆነ በስተቀር ሁሉም ንጥረ ነገሮች ካሉ ( ሀ ii) ከዜሮ ጋር እኩል ናቸው። ለምሳሌ

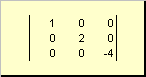
ሩዝ. 8 ሰያፍ ማትሪክስ

ማትሪክስ ሀአናት ተብሎ ይጠራል ሦስት ማዕዘንከዲያግናል በታች ያሉት ሁሉም ንጥረ ነገሮች ከዜሮ ጋር እኩል ከሆኑ፣ ማለትም ሀ ij= 0፣ በ እኔ>ጄ. ለምሳሌ

ሩዝ. 9 የላይኛው የሶስት ማዕዘን ማትሪክስ

የታችኛው የሶስት ማዕዘን ማትሪክስ በተመሳሳይ መልኩ ይገለጻል.

ማትሪክስ ሀተብሎ ይጠራል የተመጣጠነ፣ ከሆነ ሀ t = ሀ. በሌላ ቃል ሀ ij = ሀ ጂ. ለምሳሌ

ሩዝ. 10 ሲሜትሪክ ማትሪክስ

ማትሪክስ ሀተብሎ ይጠራል orthogonal፣ ከሆነ

ሀቲ ሀ = አ.አ. t = አይ.

ማትሪክስ ይባላል የተለመደከሆነ

1.5. መከታተያ እና መወሰኛ

ቀጥሎካሬ ማትሪክስ ሀ(በTr የተገለፀው) ሀ) ወይም Sp( ሀ)) የሰያፍ አባሎቹ ድምር ነው፣

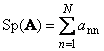
ለምሳሌ,

ሩዝ. 11 ማትሪክስ ዱካ

እንደሆነ ግልጽ ነው።

ስፒ(α ሀ= α ስፒ ሀ) እና

ስፒ( ሀ+ለ= ስፒ( ሀ)+ ስፒ( ለ).

መሆኑን ማሳየት ይቻላል።

ስፒ( ሀ= ስፒ( ሀቲ)፣ ስፒ( አይ) = ኤን,

እና እንደዚሁም

ስፒ( AB= ስፒ( ቢ.ኤ.).

የካሬ ማትሪክስ ሌላ አስፈላጊ ባህሪ የእሱ ነው። የሚወስን(የተገለጸው det) ሀ))። በአጠቃላይ ጉዳይ ላይ ወሳኙን መወሰን በጣም ከባድ ነው, ስለዚህ በጣም ቀላል በሆነው አማራጭ - ማትሪክስ እንጀምራለን. ሀልኬት (2×2)። ከዚያም

ለ(3×3) ማትሪክስ ወሳኙ እኩል ይሆናል።

በማትሪክስ ሁኔታ ( ኤን× ኤን) የሚወስነው እንደ ድምር 1·2·3· ... · ይሰላል። ኤን= ኤን! ውሎች, እያንዳንዳቸው እኩል ናቸው

ኢንዴክሶች ክ 1 , ክ 2 ,..., k Nእንደ ሁሉም ሊሆኑ የሚችሉ የታዘዙ ቅስቀሳዎች ተብለው ይገለጻሉ። አርበስብስቡ ውስጥ ያሉ ቁጥሮች (1 ፣ 2 ፣ ... ፣ ኤን). የማትሪክስ ወሳኙን ማስላት ውስብስብ ሂደት ነው, በተግባር ደግሞ ልዩ ፕሮግራሞችን በመጠቀም ይከናወናል. ለምሳሌ,

ሩዝ. 12 ማትሪክስ መወሰኛ

ግልጽ የሆኑትን ባህሪያት ብቻ እናስተውል.

det( አይ= 1, det( ሀ= ዴት( ሀቲ)

det( AB= ዴት( ሀ) det( ለ).

1.6. ቬክተሮች

ማትሪክስ አንድ አምድ ብቻ ከሆነ ( ጄ= 1), ከዚያም እንዲህ ዓይነቱ ነገር ይባላል ቬክተር. ይበልጥ በትክክል፣ የአምድ ቬክተር። ለምሳሌ

አንድ ሰው ለምሳሌ አንድ ረድፍ ያካተቱ ማትሪክቶችን ግምት ውስጥ ማስገባት ይችላል

ይህ ነገር ቬክተር ነው, ግን ረድፍ ቬክተር. መረጃን በሚተነተንበት ጊዜ ከየትኞቹ ቬክተሮች ጋር እየተገናኘን እንደሆነ መረዳት አስፈላጊ ነው - አምዶች ወይም ረድፎች. ስለዚህ ለአንድ ናሙና የሚወሰደው ስፔክትረም እንደ ረድፍ ቬክተር ሊቆጠር ይችላል. ከዚያ ለሁሉም ናሙናዎች በተወሰነ የሞገድ ርዝመት ላይ ያለው የእይታ ኢንቴንቲቲስ ስብስብ እንደ አምድ ቬክተር መታየት አለበት።

የቬክተር ልኬት የንጥረቶቹ ብዛት ነው።

ማንኛውም የዓምድ ቬክተር በመለወጥ ወደ ረድፍ ቬክተር ሊለወጥ እንደሚችል ግልጽ ነው, ማለትም.

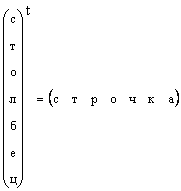
የቬክተሩ ቅርፅ በተለየ ሁኔታ ካልተገለጸ ነገር ግን በቀላሉ ቬክተር ነው ከተባለ፣ ያ ማለት የአምድ ቬክተር ማለት ነው። እኛም ይህን ደንብ እናከብራለን። ቬክተር በትናንሽ ሆሄ፣ ቀጥ ያለ፣ በደማቅ ፊደል ይገለጻል። ዜሮ ቬክተር ሁሉም ንጥረ ነገሮች ዜሮ የሆኑ ቬክተር ነው። የተሰየመ ነው። 0 .

1.7. ከቬክተሮች ጋር በጣም ቀላሉ ስራዎች

ቬክተሮች ልክ እንደ ማትሪክስ በቁጥር ሊጨመሩ እና ሊባዙ ይችላሉ። ለምሳሌ,

ሩዝ. 13 ከቬክተሮች ጋር የሚሰሩ ስራዎች

ሁለት ቬክተሮች xእና yተብለው ይጠራሉ ኮላይኔር, እንደዚህ ያለ ቁጥር α ካለ

1.8. የቬክተሮች ምርቶች

ተመሳሳይ መጠን ያላቸው ሁለት ቬክተሮች ኤንሊባዛ ይችላል. ሁለት ቬክተሮች ይኑር x = (x 1 , x 2 ,...,x N) t እና y = (y 1 , y 2 ,...,y N) ቲ. በረድፍ-በ-አምድ ማባዛት ህግ በመመራት፣ ከነሱ ሁለት ምርቶችን መፃፍ እንችላለን፡- xቲ yእና xyቲ. የመጀመሪያ ስራ

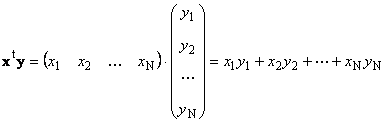
ተብሎ ይጠራል ስካላርወይም ውስጣዊ. ውጤቱም ቁጥር ነው። እሱ ደግሞ በ ( x,y)= xቲ y. ለምሳሌ,

ሩዝ. 14 ውስጣዊ (ስካላር) ምርት

ሁለተኛ ክፍል

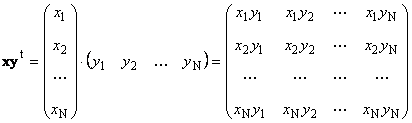
ተብሎ ይጠራል ውጫዊ. ውጤቱ የልኬት ማትሪክስ ነው ( ኤን× ኤን). ለምሳሌ,

ሩዝ. 15 ውጫዊ ሥራ

ስኬር ምርታቸው ዜሮ የሆነባቸው ቬክተሮች ተጠርተዋል። orthogonal.

1.9. የቬክተር መደበኛ

ከራሱ ጋር የቬክተር ስክላር ምርት ስካላር ካሬ ይባላል። ይህ ዋጋ

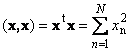
ካሬ ይገልጻል ርዝመትቬክተር x. ርዝመትን ለማመልከት (በተጨማሪም ይባላል ደንቡ vector) ማስታወሻው ጥቅም ላይ ይውላል

ለምሳሌ,

ሩዝ. 16 የቬክተር መደበኛ

የክፍል ርዝመት ቬክተር (|| x|| = 1) መደበኛ ተብሎ ይጠራል. ዜሮ ያልሆነ ቬክተር ( x ≠ 0 ) ርዝመቱን በመከፋፈል መደበኛ ሊሆን ይችላል, ማለትም. x = ||x|| (x/||x||) = ||x|| ሠ. እዚህ ሠ = x/||x|| - መደበኛ ቬክተር.

ቬክተሮች ሁሉም መደበኛ እና ጥንድ ኦርቶጎን ከሆኑ ኦርቶኖርማል ይባላሉ.

1.10. በቬክተሮች መካከል አንግል

የ scalar ምርት ይወስናል እና ጥግφ በሁለት ቬክተሮች መካከል xእና y

ቬክተሮቹ orthogonal ከሆኑ, ከዚያም cosφ = 0 እና φ = π/2, እና ኮላይነር ከሆኑ, ከዚያም cosφ = 1 እና φ = 0.

1.11. የማትሪክስ የቬክተር ውክልና

እያንዳንዱ ማትሪክስ ሀመጠን አይ× ጄእንደ የቬክተሮች ስብስብ ሊወከል ይችላል

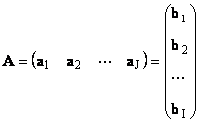
እዚህ እያንዳንዱ ቬክተር ሀ ጄነው። ጄኛ አምድ ፣ እና የረድፉ ቬክተር ለ እኔነው። እኔየማትሪክስ ኛ ረድፍ ሀ

1.12. በመስመር ላይ ጥገኛ የሆኑ ቬክተሮች

ተመሳሳይ መጠን ያላቸው ቬክተሮች ( ኤን) ልክ እንደ ማትሪክስ በቁጥር ሊጨመር እና ሊባዛ ይችላል። ውጤቱም ተመሳሳይ መጠን ያለው ቬክተር ይሆናል. ተመሳሳይ መጠን ያላቸው በርካታ ቬክተሮች ይኑር x 1 , x 2 ,...,x K እና ተመሳሳይ የቁጥሮች ቁጥር α 1, α 2,...,α ኬ. ቬክተር

y= α 1 x 1 + α 2 x 2 +...+ α ኬ x ኬ

ተብሎ ይጠራል መስመራዊ ጥምረትቬክተሮች x ክ .

እንደዚህ ያሉ ዜሮ ያልሆኑ ቁጥሮች ካሉ α ክ ≠ 0, ክ = 1,..., ኬ, ምንድን y = 0 , ከዚያ እንደዚህ አይነት የቬክተሮች ስብስብ x ክተብሎ ይጠራል በመስመር ላይ ጥገኛ. ያለበለዚያ ቬክተሮች ከመስመር ነፃ ናቸው ተብሏል። ለምሳሌ, ቬክተሮች x 1 = (2, 2) t እና x 2 = (-1, -1) t በመስመር ላይ ጥገኛ ናቸው, ምክንያቱም x 1 +2x 2 = 0

1.13. ማትሪክስ ደረጃ

ስብስብን አስቡበት ኬቬክተሮች x 1 , x 2 ,...,x ኬልኬቶች ኤን. የዚህ የቬክተር ስርዓት ደረጃ ከፍተኛው የመስመር ላይ ገለልተኛ የቬክተሮች ብዛት ነው. ለምሳሌ በስብስቡ ውስጥ

ሁለት ቀጥታ ገለልተኛ ቬክተሮች ብቻ አሉ ለምሳሌ x 1 እና x 2, ስለዚህ ደረጃው 2 ነው.

በአንድ ስብስብ ውስጥ ከነሱ ልኬት በላይ ብዙ ቬክተሮች ካሉ ግልጽ ነው። ኬ>ኤን), ከዚያ እነሱ በግድ በመስመር ላይ ጥገኛ ናቸው.

ማትሪክስ ደረጃ(በደረጃ የተገለፀው) ሀ)) በውስጡ የያዘው የቬክተር ስርዓት ደረጃ ነው. ምንም እንኳን ማንኛውም ማትሪክስ በሁለት መንገድ ሊወከል ቢችልም (አምድ ወይም ረድፎች ቬክተር) ይህ የደረጃውን ዋጋ አይጎዳውም, ምክንያቱም

1.14. የተገላቢጦሽ ማትሪክስ

ካሬ ማትሪክስ ሀልዩ ነገር ካለው ያልተበላሸ ይባላል የተገላቢጦሽማትሪክስ ሀ-1, በሁኔታዎች ይወሰናል

አ.አ. −1 = ሀ −1 ሀ = አይ.

የተገላቢጦሽ ማትሪክስ ለሁሉም ማትሪክስ የለም። ያለመበላሸት አስፈላጊ እና በቂ ሁኔታ ነው

det( ሀ≠ 0 ወይም ደረጃ( ሀ) = ኤን.

ማትሪክስ መገልበጥ ልዩ ፕሮግራሞች ያሉበት ውስብስብ ሂደት ነው. ለምሳሌ,

ሩዝ. 17 ማትሪክስ ተገላቢጦሽ

ለቀላል ጉዳይ ቀመሮችን እናቅርብ - 2 × 2 ማትሪክስ

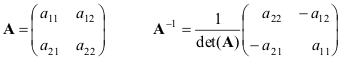
ማትሪክስ ከሆነ ሀእና ለያልተበላሹ ናቸው, እንግዲህ

(AB) −1 = ለ −1 ሀ −1 .

1.15. Pseudoinverse ማትሪክስ

ማትሪክስ ከሆነ ሀነጠላ ነው እና የተገላቢጦሽ ማትሪክስ የለም, ከዚያ በአንዳንድ ሁኔታዎች መጠቀም ይችላሉ pseudoinverseማትሪክስ, እሱም እንደ ማትሪክስ ይገለጻል ሀ+ ያ

አ.አ. + ሀ = ሀ.

pseudoinverse ማትሪክስ አንድ ብቻ አይደለም እና ቅጹ በግንባታው ዘዴ ላይ የተመሰረተ ነው. ለምሳሌ, ለአራት ማዕዘን ቅርጽ ያለው ማትሪክስ የ Moore-Penrose ዘዴን መጠቀም ይችላሉ.

የአምዶች ቁጥር ከረድፎች ብዛት ያነሰ ከሆነ, ከዚያ

ሀ + =(ሀቲ ሀ) −1 ሀቲ

ለምሳሌ,

ሩዝ. 17a የውሸት ማትሪክስ ግልበጣ

የአምዶች ቁጥር ከረድፎች ብዛት በላይ ከሆነ, ከዚያ

ሀ + =ሀቲ ( አ.አ.ቲ) −1

1.16. ቬክተርን በማትሪክስ ማባዛት።

ቬክተር xበማትሪክስ ሊባዛ ይችላል ሀተስማሚ መጠን. በዚህ ሁኔታ, የዓምድ ቬክተር በቀኝ በኩል ይባዛል አክስ, እና የቬክተር ረድፍ በግራ በኩል ነው xቲ ሀ. የቬክተር ልኬት ከሆነ ጄ, እና የማትሪክስ ልኬት አይ× ጄከዚያም ውጤቱ የልኬት ቬክተር ይሆናል አይ. ለምሳሌ,

ሩዝ. 18 ቬክተርን በማትሪክስ ማባዛት።

ማትሪክስ ከሆነ ሀ- ካሬ ( አይ× አይ), ከዚያም ቬክተር y = አክስተመሳሳይ መጠን አለው x. እንደሆነ ግልጽ ነው።

ሀ(α 1 x 1 + α 2 x 2) = α 1 አክስ 1 + α 2 አክስ 2 .

ስለዚህ ማትሪክስ እንደ የቬክተሮች ቀጥተኛ ለውጥ ተደርጎ ሊወሰድ ይችላል። በተለየ ሁኔታ Ix = x, ኦክስ = 0 .

2. ተጨማሪ መረጃ

2.1. የመስመር እኩልታዎች ስርዓቶች

ፍቀድ ሀ- ማትሪክስ መጠን አይ× ጄ, ኤ ለ- ልኬት ቬክተር ጄ. እኩልነቱን አስቡበት

አክስ = ለ

ከቬክተር አንፃር x, ልኬቶች አይ. በመሠረቱ, እሱ ስርዓት ነው አይጋር መስመራዊ እኩልታዎች ጄየማይታወቅ x 1 ,...,x ጄ. መፍትሄ የሚኖረው ከሆነ እና ከሆነ ብቻ ነው።

ደረጃ( ሀ) = ደረጃ ለ) = አር,

የት ለየተራዘመ የልኬቶች ማትሪክስ ነው። አይ×( ጄ+1), ማትሪክስ ያካተተ ሀ, በአምድ ተጨምሯል ለ, ለ = (ሀ ለ). አለበለዚያ, እኩልታዎቹ የማይጣጣሙ ናቸው.

ከሆነ አር = አይ = ጄ, ከዚያም መፍትሔው ልዩ ነው

x = ሀ −1 ለ.

ከሆነ አር < አይ, ከዚያም በመስመራዊ ጥምረት ሊገለጹ የሚችሉ ብዙ የተለያዩ መፍትሄዎች አሉ ጄ−አርቬክተሮች. ተመሳሳይነት ያላቸው እኩልታዎች ስርዓት አክስ = 0 ከካሬ ማትሪክስ ጋር ሀ (ኤን× ኤንቀላል ያልሆነ መፍትሄ አለው ( x ≠ 0 ) ከሆነ እና ከሆነ ብቻ det ( ሀ) = 0. ከሆነ አር= ደረጃ( ሀ)<ኤን, ከዚያም አሉ ኤን−አርቀጥተኛ ገለልተኛ መፍትሄዎች.

2.2. ባለሁለት እና አራት ማዕዘን ቅርጾች

ከሆነ ሀካሬ ማትሪክስ ነው, እና xእና y- የሚዛመደው ልኬት ቬክተር ፣ ከዚያ የቅጹ scalar ምርት xቲ አይተብሎ ይጠራል ቢሊነርበማትሪክስ የተገለጸ ቅጽ ሀ. በ x = yአገላለጽ xቲ አክስተብሎ ይጠራል አራት ማዕዘንቅጽ.

2.3. አዎንታዊ ትክክለኛ ማትሪክስ

ካሬ ማትሪክስ ሀተብሎ ይጠራል አዎንታዊ የተወሰነ, ለማንኛውም ዜሮ ያልሆነ ቬክተር ከሆነ x ≠ 0 ,

xቲ አክስ > 0.

በተመሳሳይ መልኩ ተገልጿል አሉታዊ (xቲ አክስ < 0), አሉታዊ ያልሆነ (xቲ አክስ≥ 0) እና አሉታዊ (xቲ አክስ≤ 0) የተወሰኑ ማትሪክስ.

2.4. Cholesky መበስበስ

የሲሜትሪክ ማትሪክስ ከሆነ ሀአወንታዊ ነው፣ ከዚያ ልዩ የሆነ የሶስት ማዕዘን ማትሪክስ አለ። ዩከአዎንታዊ አካላት ጋር, ለዚህም

ሀ = ዩቲ ዩ.

ለምሳሌ,

ሩዝ. 19 Cholesky መበስበስ

2.5. የዋልታ መበስበስ

ፍቀድ ሀነጠላ ያልሆነ የካሬ ማትሪክስ ልኬት ነው። ኤን× ኤን. ከዚያም ልዩ የሆነ ነገር አለ የዋልታአፈጻጸም

ሀ = ኤስ.አር.

የት ኤስአሉታዊ ያልሆነ ሲሜትሪክ ማትሪክስ ነው፣ እና አር orthogonal ማትሪክስ ነው። ማትሪክስ ኤስእና አርበግልፅ ሊገለጽ ይችላል፡-

ኤስ 2 = አ.አ.ቲ ወይም ኤስ = (አ.አ. t) ½ እና አር = ኤስ −1 ሀ = (አ.አ. t) -½ ሀ.

ለምሳሌ,

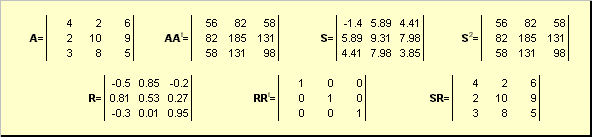
ሩዝ. 20 የዋልታ መበስበስ

ማትሪክስ ከሆነ ሀየተበላሸ ነው, ከዚያም መበስበስ ልዩ አይደለም - ማለትም: ኤስአሁንም ብቻውን, ግን አርምናልባት ብዙ። የዋልታ መበስበስ ማትሪክስ ይወክላል ሀእንደ መጭመቂያ / ማራዘሚያ ጥምረት ኤስእና መዞር አር.

2.6. Eigenvectors እና eigenvalues

ፍቀድ ሀካሬ ማትሪክስ ነው። ቬክተር ቁተብሎ ይጠራል eigenvectorማትሪክስ ሀ፣ ከሆነ

አቭ = λ ቁ,

ቁጥሩ λ የሚጠራበት ኢጂን ዋጋማትሪክስ ሀ. ስለዚህ, ማትሪክስ የሚያከናውነው ለውጥ ሀከቬክተር በላይ ቁ, ወደ ቀላል መወጠር ወይም መጨናነቅ ከ Coefficient λ ጋር ይመጣል. eigenvector በቋሚ α ≠ 0 እስከ ማባዛት የሚወሰን ነው፣ ማለትም. ከሆነ ቁኢጂንቬክተር ነው, ከዚያም α ቁ- እንዲሁም eigenvector.

2.7. ኢጅን እሴቶች

በማትሪክስ ሀ፣ ልኬት ( ኤን× ኤን) በላይ ሊሆን አይችልም። ኤንኢጂን እሴቶች. ያረካሉ የባህሪ እኩልታ

det( ሀ − λ አይ) = 0,

ይህም የአልጀብራ እኩልነት ነው። ኤን- ትዕዛዝ. በተለይም ለ 2 × 2 ማትሪክስ የባህሪው እኩልታ ቅፅ አለው

ለምሳሌ,

ሩዝ. 21 Eigenvalues

የ eigenvalues ​​ስብስብ λ 1፣...፣ λ ኤንማትሪክስ ሀተብሎ ይጠራል ስፔክትረም ሀ.

ስፔክትረም የተለያዩ ባህሪያት አሉት. በተለየ ሁኔታ

det( ሀ) = λ 1 ×...×λ ኤንስፒ ሀ) = λ 1 +...+λ ኤን.

የዘፈቀደ ማትሪክስ እሴቶቹ ውስብስብ ቁጥሮች ሊሆኑ ይችላሉ ፣ ግን ማትሪክስ ተመሳሳይ ከሆነ ( ሀ t = ሀ), ከዚያ የእሱ ኢጂን እሴቶቹ እውነተኛ ናቸው።

2.8. ኢጂንቬክተሮች

በማትሪክስ ሀ፣ ልኬት ( ኤን× ኤን) በላይ ሊሆን አይችልም። ኤን eigenvectors, እያንዳንዳቸው ከራሳቸው ኢጂን ዋጋ ጋር ይዛመዳሉ. ኢጂንቬክተሩን ለመወሰን ቁ nተመሳሳይነት ያላቸውን እኩልታዎች ስርዓት መፍታት ያስፈልጋል

(ሀ − λ n አይ)ቁ n = 0 .

ከ det ጀምሮ ቀላል ያልሆነ መፍትሄ አለው ሀ -λ n አይ) = 0.

ለምሳሌ,

ሩዝ. 22 ኢጂንቬክተሮች

የሲሜትሪክ ማትሪክስ ኢጂንቬክተሮች orthogonal ናቸው.