Find operatorens egenværdier. Egenværdier (tal) og egenvektorer Eksempler på løsninger

Diagonale matricer har den enkleste struktur. Spørgsmålet opstår, om det er muligt at finde et grundlag, hvor den lineære operators matrix ville have en diagonal form. Et sådant grundlag findes.
Lad os få et lineært rum R n og en lineær operator A, der virker i det; i dette tilfælde tager operator A R n ind i sig selv, det vil sige A:R n → R n .

Definition. En ikke-nul vektor kaldes en egenvektor for operatoren A, hvis operatoren A oversættes til en kollineær vektor, dvs. Tallet λ kaldes egenværdien eller egenværdien af ​​operatoren A, svarende til egenvektoren.
Lad os bemærke nogle egenskaber ved egenværdier og egenvektorer.
1. Enhver lineær kombination af egenvektorer operator A svarende til den samme egenværdi λ er en egenvektor med samme egenværdi.
2. Egenvektorer operator A med parvis forskellige egenværdier λ 1 , λ 2 , …, λ m er lineært uafhængige.
3. Hvis egenværdierne λ 1 =λ 2 = λ m = λ, så svarer egenværdien λ til ikke mere end m lineært uafhængige egenvektorer.

Så hvis der er n lineært uafhængige egenvektorer , svarende til forskellige egenværdier λ 1, λ 2, ..., λ n, så er de lineært uafhængige, derfor kan de tages som grundlag for rummet R n. Lad os finde formen af ​​matrixen for den lineære operator A på basis af dens egenvektorer, for hvilke vi vil handle med operatoren A på basisvektorerne: Derefter .
Således har matrixen af ​​den lineære operator A på grundlag af dens egenvektorer en diagonal form, og egenværdierne for operatoren A er langs diagonalen.
Er der et andet grundlag, hvor matricen har en diagonal form? Svaret på dette spørgsmål er givet af følgende sætning.

Sætning. Matrixen for en lineær operator A i basis (i = 1..n) har en diagonal form, hvis og kun hvis alle vektorerne i basis er egenvektorer af operatoren A.

Regel for at finde egenværdier og egenvektorer

. (*)

(1)
Hvor - lineær operatormatrix.

System (1) har en løsning, der ikke er nul, hvis dets determinant D er lig med nul

Eksempel 12. Den lineære operator A virker i R 3 efter loven, hvor x 1, x 2, .., x n er koordinaterne til vektoren i basis , , . Find egenværdierne og egenvektorerne for denne operator.
Løsning. Vi bygger matrixen for denne operatør:
.
Vi opretter et system til bestemmelse af koordinaterne for egenvektorer:

Vi sammensætter en karakteristisk ligning og løser den:

.
λ 1,2 = -1, λ 3 = 3.
Ved at indsætte λ = -1 i systemet har vi:
eller
Fordi , så er der to afhængige variable og en fri variabel.
Lad x 1 være en fri ukendt, så Vi løser dette system på enhver måde og finder den generelle løsning af dette system: Det grundlæggende system af løsninger består af én løsning, da n - r = 3 - 2 = 1.
Sættet af egenvektorer svarende til egenværdien λ = -1 har formen: , hvor x 1 er et hvilket som helst andet tal end nul. Lad os vælge en vektor fra dette sæt, for eksempel ved at sætte x 1 = 1: .
På samme måde finder vi egenvektoren svarende til egenværdien λ = 3: .
I rummet R 3 består basis af tre lineært uafhængige vektorer, men vi modtog kun to lineært uafhængige egenvektorer, hvorfra grundlaget i R 3 ikke kan sammensættes. Derfor kan vi ikke reducere matrixen A af en lineær operator til diagonal form.

Eksempel 13. Givet en matrix .
1. Bevis at vektoren er en egenvektor af matrix A. Find egenværdien svarende til denne egenvektor.
2. Find et grundlag, hvor matrix A har en diagonal form.
Løsning.
1. Hvis , så er en egenvektor

.
Vektor (1, 8, -1) er en egenvektor. Egenværdi λ = -1.
Matrixen har en diagonal form i en basis bestående af egenvektorer. En af dem er berømt. Lad os finde resten.
Vi leder efter egenvektorer fra systemet:

Karakteristisk ligning: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ2 - 1) = 0
λ1 = -3, λ2 = 1, λ3 = -1.
Lad os finde egenvektoren svarende til egenværdien λ = -3:

Rangeringen af ​​matrixen for dette system er to og lig med antallet af ukendte, så dette system har kun en nulløsning x 1 = x 3 = 0. x 2 her kan være alt andet end nul, for eksempel x 2 = 1. Vektoren (0 ,1,0) er således en egenvektor svarende til λ = -3. Lad os tjekke:
.
Hvis λ = 1, får vi systemet
Rangen af ​​matrixen er to. Vi krydser den sidste ligning over.
Lad x 3 være en gratis ukendt. Derefter x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Hvis vi antager x 3 = 1, har vi (-3,-9,1) - en egenvektor svarende til egenværdien λ = 1. Tjek:

.
Da egenværdierne er reelle og distinkte, er vektorerne, der svarer til dem, lineært uafhængige, så de kan tages som basis i R 3 . Således i grundlaget , , matrix A har formen:
.
Ikke hver matrix af en lineær operator A:R n → R n kan reduceres til diagonal form, da der for nogle lineære operatorer kan være mindre end n lineære uafhængige egenvektorer. Men hvis matricen er symmetrisk, svarer roden af ​​den karakteristiske ligning af multiplicitet m til nøjagtigt m lineært uafhængige vektorer.

Definition. En symmetrisk matrix er en kvadratisk matrix, hvor de elementer, der er symmetriske om hoveddiagonalen, er lige store, det vil sige, hvor .
Noter. 1. Alle egenværdier af en symmetrisk matrix er reelle.
2. Egenvektorerne af en symmetrisk matrix svarende til parvis forskellige egenværdier er ortogonale.
Som en af ​​de mange anvendelser af det undersøgte apparat betragter vi problemet med at bestemme typen af ​​en andenordenskurve.

Egenværdier (tal) og egenvektorer.
Eksempler på løsninger

Vær dig selv

Af begge ligninger følger det, at .

Lad os sige det så: .

Som resultat: – anden egenvektor.

Lad os gentage de vigtige punkter i beslutningen:

– det resulterende system har bestemt en generel løsning (ligningerne er lineært afhængige);

– vi vælger "y" på en sådan måde, at det er heltal, og den første "x"-koordinat er heltal, positivt og så lille som muligt.

– vi kontrollerer, at den bestemte løsning opfylder hver ligning i systemet.

Svar .

Der var ret nok mellemliggende "checkpoints", så kontrol af ligestilling er i princippet unødvendig.

I forskellige informationskilder er egenvektorernes koordinater ofte ikke skrevet i kolonner, men i rækker, for eksempel: (og for at være ærlig er jeg selv vant til at skrive dem ned i linjer). Denne mulighed er acceptabel, men i lyset af emnet lineære transformationer teknisk mere praktisk at bruge kolonnevektorer.

Måske virkede løsningen meget lang for dig, men det er kun fordi jeg kommenterede det første eksempel meget detaljeret.

Eksempel 2

Matricer

Lad os træne på egen hånd! Et omtrentligt eksempel på en afsluttende opgave i slutningen af ​​lektionen.

Nogle gange skal du udføre en ekstra opgave, nemlig:

skriv den kanoniske matrix-nedbrydning

Hvad er det?

Hvis matrixens egenvektorer dannes basis, så kan det repræsenteres som:

Hvor er en matrix sammensat af koordinater af egenvektorer, - diagonal matrix med tilsvarende egenværdier.

Denne matrixnedbrydning kaldes kanonisk eller diagonal.

Lad os se på matrixen i det første eksempel. Dens egenvektorer lineært uafhængig(ikke-kollineær) og danner et grundlag. Lad os lave en matrix af deres koordinater:

På hoveddiagonal matricer i passende rækkefølge egenværdierne er placeret, og de resterende elementer er lig med nul:
– Jeg understreger endnu en gang vigtigheden af ​​orden: "to" svarer til 1. vektor og er derfor placeret i 1. kolonne, "tre" - til 2. vektor.

Bruger den sædvanlige algoritme til at finde omvendt matrix eller Gauss-Jordan metode vi finder . Nej, det er ikke en tastefejl! - før dig er en sjælden begivenhed, som en solformørkelse, hvor det omvendte faldt sammen med den oprindelige matrix.

Det er tilbage at skrive ned den kanoniske nedbrydning af matricen:

Systemet kan løses ved hjælp af elementære transformationer, og i de følgende eksempler vil vi ty til denne metode. Men her fungerer "skole"-metoden meget hurtigere. Fra den 3. ligning udtrykker vi: – substituer ind i den anden ligning:

Da den første koordinat er nul, får vi et system, fra hver ligning, hvoraf det følger, at .

Og igen være opmærksom på den obligatoriske tilstedeværelse af et lineært forhold. Hvis der kun opnås en triviel løsning , så blev egenværdien enten fundet forkert, eller også blev systemet kompileret/løst med en fejl.

Kompakte koordinater giver værdien

Egenvektor:

Og endnu en gang tjekker vi, at løsningen er fundet opfylder enhver ligning i systemet. I efterfølgende afsnit og i efterfølgende opgaver anbefaler jeg at tage dette ønske som en obligatorisk regel.

2) For egenværdien får vi ved hjælp af samme princip følgende system:

Fra systemets 2. ligning udtrykker vi: – erstatter i den tredje ligning:

Da "zeta"-koordinaten er lig med nul, får vi et system fra hver ligning, hvoraf en lineær afhængighed følger.

Lade

Tjek at løsningen opfylder enhver ligning i systemet.

Egenvektoren er således: .

3) Og endelig svarer systemet til egenværdien:

Den anden ligning ser den enkleste ud, så lad os udtrykke den og erstatte den med 1. og 3. ligning:

Alt er fint - der er opstået et lineært forhold, som vi erstatter med udtrykket:

Som et resultat blev "x" og "y" udtrykt gennem "z": . I praksis er det ikke nødvendigt at opnå netop sådanne relationer; i nogle tilfælde er det mere bekvemt at udtrykke både gennem eller gennem . Eller endda "tog" - for eksempel "X" til "I" og "I" til "Z"

Lad os sige det så:

Vi tjekker, at løsningen er fundet opfylder hver ligning i systemet og skriver den tredje egenvektor

Svar: egenvektorer:

Geometrisk definerer disse vektorer tre forskellige rumlige retninger ("Der og tilbage igen"), ifølge hvilken lineær transformation transformerer ikke-nul vektorer (egenvektorer) til kollineære vektorer.

Hvis betingelsen krævede at finde den kanoniske nedbrydning, så er dette muligt her, fordi forskellige egenværdier svarer til forskellige lineært uafhængige egenvektorer. At lave en matrix fra deres koordinater, en diagonal matrix fra relevant egenværdier og find omvendt matrix .

Hvis du efter betingelse skal skrive lineær transformationsmatrix i basis af egenvektorer, så giver vi svaret i skemaet . Der er en forskel, og forskellen er betydelig! Fordi denne matrix er "de" matrixen.

Et problem med enklere beregninger, som du selv kan løse:

Eksempel 5

Find egenvektorer for en lineær transformation givet af en matrix

Når du finder dine egne tal, så prøv ikke at gå hele vejen til et 3. grads polynomium. Derudover kan dine systemløsninger afvige fra mine løsninger - her er der ingen sikkerhed; og de vektorer, du finder, kan afvige fra prøvevektorerne op til proportionaliteten af ​​deres respektive koordinater. For eksempel og. Det er mere æstetisk tiltalende at præsentere svaret i formularen, men det er okay, hvis du stopper ved den anden mulighed. Der er dog rimelige grænser for alt; versionen ser ikke længere særlig godt ud.

Et omtrentligt endeligt udsnit af opgaven i slutningen af ​​lektionen.

Hvordan løser man problemet i tilfælde af flere egenværdier?

Den generelle algoritme forbliver den samme, men den har sine egne karakteristika, og det er tilrådeligt at holde nogle dele af løsningen i en mere streng akademisk stil:

Eksempel 6

Find egenværdier og egenvektorer

Løsning

Lad os selvfølgelig bruge den fantastiske første kolonne med stort:

Og efter at have faktoriseret det kvadratiske trinomium:

Som et resultat opnås egenværdier, hvoraf to er multipla.

Lad os finde egenvektorerne:

1) Lad os beskæftige os med en enlig soldat i henhold til en "forenklet" ordning:

Fra de sidste to ligninger er ligheden tydeligt synlig, som naturligvis skal erstattes i systemets 1. ligning:

Du finder ikke en bedre kombination:
Egenvektor:

2-3) Nu fjerner vi et par vagtposter. I dette tilfælde kan det vise sig enten to eller en egenvektor. Uanset røddernes mangfoldighed erstatter vi værdien med determinanten hvilket bringer os det næste homogent system af lineære ligninger:

Egenvektorer er præcis vektorer
grundlæggende system af løsninger

Faktisk, gennem hele lektionen gjorde vi ikke andet end at finde vektorerne for det grundlæggende system. Det er bare det, at foreløbig var denne periode ikke særlig påkrævet. I øvrigt de der kloge elever, der savnede emnet i camouflagedragter homogene ligninger, bliver tvunget til at ryge det nu.

Den eneste handling var at fjerne de ekstra linjer. Resultatet er en en-til-tre matrix med et formelt "trin" i midten.
– grundvariabel – frie variable. Der er derfor to frie variabler der er også to vektorer af det fundamentale system.

Lad os udtrykke den grundlæggende variabel i form af frie variable: . Nulmultiplikatoren foran "X" gør det muligt for den at antage absolut alle værdier (hvilket er tydeligt synligt fra ligningssystemet).

I forbindelse med dette problem er det mere bekvemt at skrive den generelle løsning ikke i en række, men i en kolonne:

Parret svarer til en egenvektor:
Parret svarer til en egenvektor:

Bemærk : sofistikerede læsere kan vælge disse vektorer mundtligt - blot ved at analysere systemet , men en vis viden er nødvendig her: der er tre variabler, systemmatrix rang- en, hvilket betyder grundlæggende beslutningssystem består af 3 – 1 = 2 vektorer. De fundne vektorer er dog tydeligt synlige selv uden denne viden, rent intuitivt. I dette tilfælde vil den tredje vektor blive skrevet endnu mere "smukt": . Jeg advarer dig dog om, at i et andet eksempel er et simpelt valg muligvis ikke muligt, hvorfor klausulen er beregnet til erfarne mennesker. Derudover, hvorfor ikke tage for eksempel som den tredje vektor? Dens koordinater opfylder jo også hver ligning i systemet og vektorerne lineært uafhængig. Denne mulighed er i princippet egnet, men "skæv", da den "anden" vektor er en lineær kombination af vektorer i det grundlæggende system.

Svar: egenværdier: , egenvektorer:

Et lignende eksempel på en uafhængig løsning:

Eksempel 7

Find egenværdier og egenvektorer

En omtrentlig prøve af det endelige design i slutningen af ​​lektionen.

Det skal bemærkes, at i både det 6. og det 7. eksempel opnås en tripel af lineært uafhængige egenvektorer, og derfor er den oprindelige matrix repræsentabel i den kanoniske dekomponering. Men sådanne hindbær sker ikke i alle tilfælde:

Eksempel 8

Løsning: Lad os skabe og løse den karakteristiske ligning:

Lad os udvide determinanten i den første kolonne:

Vi udfører yderligere forenklinger i henhold til den betragtede metode, hvor vi undgår tredjegradspolynomiet:

– egenværdier.

Lad os finde egenvektorerne:

1) Der er ingen problemer med roden:

Bliv ikke overrasket, ud over sættet er der også variabler i brug - der er ingen forskel her.

Fra 3. ligning udtrykker vi det og erstatter det i 1. og 2. ligning:

Af begge ligninger følger:

Lad så:

2-3) For flere værdier får vi systemet .

Lad os nedskrive systemets matrix og ved hjælp af elementære transformationer bringe det til en trinvis form:

www.websted giver dig mulighed for at finde. Webstedet udfører beregningen. I løbet af få sekunder vil serveren give den korrekte løsning. Den karakteristiske ligning for matrixen vil være et algebraisk udtryk fundet ved hjælp af reglen for beregning af determinanten matricer matricer, mens der langs hoveddiagonalen vil være forskelle i værdierne af de diagonale elementer og variablen. Ved beregning karakteristisk ligning for matrixen online, hvert element matricer vil blive ganget med tilsvarende andre elementer matricer. Find i tilstand online kun muligt for firkantet matricer. Finder operation karakteristisk ligning for matrixen online reducerer til at beregne den algebraiske sum af produktet af elementer matricer som et resultat af at finde determinanten matricer, kun med det formål at bestemme karakteristisk ligning for matrixen online. Denne operation indtager en særlig plads i teorien matricer, giver dig mulighed for at finde egenværdier og vektorer ved hjælp af rødder. Opgaven med at finde karakteristisk ligning for matrixen online består af multiplikation af elementer matricer efterfulgt af summering af disse produkter efter en bestemt regel. www.websted finder karakteristisk ligning for matrixen givet dimension i mode online. Beregning karakteristisk ligning for matrixen online givet dens dimension er dette at finde et polynomium med numeriske eller symbolske koefficienter, fundet i henhold til reglen for beregning af determinanten matricer- som summen af ​​produkterne af de tilsvarende elementer matricer, kun med det formål at bestemme karakteristisk ligning for matrixen online. At finde et polynomium med hensyn til en variabel for en andengrad matricer, som en definition karakteristisk ligning for matrixen, almindelig i teorien matricer. Betydningen af ​​rødderne af et polynomium karakteristisk ligning for matrixen online bruges til at bestemme egenvektorer og egenværdier for matricer. Desuden, hvis determinanten matricer vil da være lig nul matrixens karakteristiske ligning vil stadig eksistere, i modsætning til det omvendte matricer. For at beregne karakteristisk ligning for matrixen eller find for flere på én gang matrix karakteristiske ligninger, skal du bruge en masse tid og kræfter, mens vores server finder i løbet af få sekunder karakteristisk ligning for matrix online. I dette tilfælde er svaret på at finde karakteristisk ligning for matrixen online vil være korrekte og med tilstrækkelig nøjagtighed, selvom tallene ved at finde karakteristisk ligning for matrixen online vil være irrationel. På siden www.websted tegnindtastninger er tilladt i elementer matricer, det er karakteristisk ligning for matrix online kan repræsenteres i generel symbolsk form ved beregning karakteristisk ligning af matrixen online. Det er nyttigt at kontrollere det opnåede svar, når du løser problemet med at finde karakteristisk ligning for matrixen online ved at bruge siden www.websted. Når du udfører operationen med at beregne et polynomium - matrixens karakteristiske ligning, skal du være forsigtig og ekstremt fokuseret, når du løser dette problem. Til gengæld vil vores side hjælpe dig med at kontrollere din beslutning om emnet karakteristisk ligning af en matrix online. Har du ikke tid til lange kontroller af løste problemer, så www.websted vil helt sikkert være et praktisk værktøj til at tjekke, når man finder og regner karakteristisk ligning for matrixen online.

En egenvektor for en kvadratisk matrix er en, der, når den ganges med en given matrix, resulterer i en kollineær vektor. Med enkle ord, når en matrix multipliceres med en egenvektor, forbliver sidstnævnte den samme, men multipliceret med et vist tal.

Definition

En egenvektor er en ikke-nul vektor V, som, når den multipliceres med en kvadratisk matrix M, selv bliver forøget med et eller andet tal λ. I algebraisk notation ser det sådan ud:

M × V = λ × V,

hvor λ er egenværdien af ​​matrixen M.

Lad os se på et numerisk eksempel. For at lette optagelsen vil tal i matrixen blive adskilt af et semikolon. Lad os have en matrix:

• M = 0; 4;
• 6; 10.

Lad os gange det med en kolonnevektor:

• V = -2;

Når vi multiplicerer en matrix med en kolonnevektor, får vi også en kolonnevektor. I strengt matematisk sprog vil formlen for at multiplicere en 2 × 2 matrix med en kolonnevektor se sådan ud:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 betyder elementet i matrix M placeret i første række og første kolonne, og M22 betyder elementet placeret i anden række og anden kolonne. For vores matrix er disse elementer lig med M11 = 0, M12 = 4, M21 = 6, M22 10. For en kolonnevektor er disse værdier lig med V11 = –2, V21 = 1. Ifølge denne formel, vi får følgende resultat af produktet af en kvadratisk matrix med en vektor:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Lad os for nemheds skyld skrive kolonnevektoren i en række. Så vi multiplicerede den kvadratiske matrix med vektoren (-2; 1), hvilket resulterede i vektoren (4; -2). Det er klart, at dette er den samme vektor ganget med λ = -2. Lambda i dette tilfælde angiver egenværdien af ​​matricen.

En egenvektor til en matrix er en kollineær vektor, det vil sige et objekt, der ikke ændrer sin position i rummet, når det multipliceres med en matrix. Begrebet kollinearitet i vektoralgebra ligner udtrykket parallelisme i geometri. I en geometrisk fortolkning er kollineære vektorer parallelt rettede segmenter af forskellig længde. Siden Euklids tid ved vi, at en linje har et uendeligt antal linjer parallelle med sig, så det er logisk at antage, at hver matrix har et uendeligt antal egenvektorer.

Fra det foregående eksempel er det klart, at egenvektorer kan være (-8; 4), og (16; -8) og (32, -16). Disse er alle kollineære vektorer svarende til egenværdien λ = -2. Når vi multiplicerer den oprindelige matrix med disse vektorer, vil vi stadig ende med en vektor, der adskiller sig fra originalen med 2 gange. Det er derfor, når man løser problemer med at finde en egenvektor, er det nødvendigt kun at finde lineært uafhængige vektorobjekter. Oftest er der for en n × n matrix et n antal egenvektorer. Vores lommeregner er designet til analyse af andenordens kvadratmatricer, så næsten altid vil resultatet finde to egenvektorer, bortset fra tilfælde hvor de falder sammen.

I eksemplet ovenfor kendte vi egenvektoren for den oprindelige matrix på forhånd og bestemte tydeligt lambdatallet. Men i praksis sker alt omvendt: egenværdierne findes først og først derefter egenvektorerne.

Løsningsalgoritme

Lad os se på den oprindelige matrix M igen og prøve at finde begge dens egenvektorer. Så matricen ser sådan ud:

• M = 0; 4;
• 6; 10.

Først skal vi bestemme egenværdien λ, som kræver beregning af determinanten af ​​følgende matrix:

• (0 - λ); 4;
• 6; (10 - λ).

Denne matrix opnås ved at trække den ukendte λ fra elementerne på hoveddiagonalen. Determinanten bestemmes ved hjælp af standardformlen:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Da vores vektor skal være ikke-nul, accepterer vi den resulterende ligning som lineært afhængig og sidestiller vores determinant detA til nul.

(0 − λ) × (10 − λ) − 24 = 0

Lad os åbne parenteserne og få den karakteristiske ligning for matricen:

λ 2 − 10λ − 24 = 0

Dette er en standard andengradsligning, der skal løses ved hjælp af en diskriminant.

D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

Roden af ​​diskriminanten er sqrt(D) = 14, derfor λ1 = -2, λ2 = 12. For hver lambda-værdi skal vi nu finde egenvektoren. Lad os udtrykke systemkoefficienterne for λ = -2.

• M - λ × E = 2; 4;
• 6; 12.

I denne formel er E identitetsmatrixen. Baseret på den resulterende matrix skaber vi et system af lineære ligninger:

2x + 4y = 6x + 12y,

hvor x og y er egenvektorelementerne.

Lad os samle alle X'erne til venstre og alle Y'erne til højre. Det er klart - 4x = 8y. Divider udtrykket med - 4 og få x = –2y. Nu kan vi bestemme den første egenvektor af matricen ved at tage alle værdier af de ukendte (husk uendeligheden af ​​lineært afhængige egenvektorer). Lad os tage y = 1, så x = –2. Derfor ser den første egenvektor ud som V1 = (–2; 1). Vend tilbage til begyndelsen af ​​artiklen. Det var dette vektorobjekt, vi gangede matricen med for at demonstrere begrebet en egenvektor.

Lad os nu finde egenvektoren for λ = 12.

• M - X x E = -12; 4
• 6; -2.

Lad os skabe det samme system af lineære ligninger;

• -12x + 4y = 6x - 2y
• -18x = -6 år
• 3x = y.

Nu tager vi x = 1, derfor y = 3. Den anden egenvektor ser således ud som V2 = (1; 3). Når man multiplicerer den oprindelige matrix med en given vektor, vil resultatet altid være den samme vektor ganget med 12. Det er her løsningsalgoritmen slutter. Nu ved du, hvordan man manuelt bestemmer egenvektoren for en matrix.

• determinant;
• spor, det vil sige summen af ​​elementerne på hoveddiagonalen;
• rang, det vil sige det maksimale antal lineært uafhængige rækker/kolonner.

Programmet fungerer i henhold til ovenstående algoritme, hvilket forkorter løsningsprocessen så meget som muligt. Det er vigtigt at påpege, at i programmet er lambda betegnet med bogstavet "c". Lad os se på et numerisk eksempel.

Eksempel på hvordan programmet fungerer

Lad os prøve at bestemme egenvektorerne for følgende matrix:

• M = 5; 13;
• 4; 14.

Lad os indtaste disse værdier i cellerne i lommeregneren og få svaret i følgende form:

• Matrix rang: 2;
• Matrixdeterminant: 18;
• Matrix-spor: 19;
• Beregning af egenvektoren: c 2 − 19,00c + 18,00 (karakteristisk ligning);
• Egenvektorberegning: 18 (første lambdaværdi);
• Egenvektorberegning: 1 (anden lambdaværdi);
• Ligningssystem for vektor 1: -13x1 + 13y1 = 4x1 − 4y1;
• Ligningssystem for vektor 2: 4x1 + 13y1 = 4x1 + 13y1;
• Egenvektor 1: (1; 1);
• Egenvektor 2: (-3,25; 1).

Således opnåede vi to lineært uafhængige egenvektorer.

Konklusion

Lineær algebra og analytisk geometri er standardfag for enhver nyuddannet ingeniørstuderende. Det store antal vektorer og matricer er skræmmende, og det er nemt at lave fejl i så besværlige beregninger. Vores program vil give eleverne mulighed for at kontrollere deres beregninger eller automatisk løse problemet med at finde en egenvektor. Der er andre lineære algebra-beregnere i vores katalog; brug dem i dine studier eller arbejde.

"Første del opstiller de bestemmelser, der er minimalt nødvendige for at forstå kemometri, og anden del indeholder de fakta, som du skal kende til for at få en dybere forståelse af metoderne til multivariat analyse. Præsentationen er illustreret med eksempler lavet i Excel-projektmappen. Matrix.xls, som ledsager dette dokument.

Links til eksempler placeres i teksten som Excel-objekter. Disse eksempler er af abstrakt karakter; de er på ingen måde knyttet til problemerne med analytisk kemi. Eksempler fra det virkelige liv på brugen af ​​matrixalgebra i kemometri diskuteres i andre tekster, der dækker en række forskellige kemometriske anvendelser.

De fleste målinger foretaget i analytisk kemi er ikke direkte, men indirekte. Det betyder, at der i forsøget i stedet for værdien af ​​den ønskede analyt C (koncentration) opnås en anden værdi x(signal), relateret, men ikke lig med C, dvs. x(C) ≠ C. Som regel typen af ​​afhængighed x(C) er ukendt, men heldigvis i analytisk kemi er de fleste målinger proportionale. Det betyder, at med stigende koncentration af C in -en gange, vil signal X stige med samme mængde, dvs. x(-en C) = et x(C). Derudover er signalerne også additive, så signalet fra en prøve, hvori to stoffer med koncentrationerne C 1 og C 2 er til stede, vil være lig summen af ​​signalerne fra hver komponent, dvs. x(C1 + C2) = x(C1)+ x(C2). Proportionalitet og additivitet giver tilsammen linearitet. Der kan gives mange eksempler for at illustrere princippet om linearitet, men det er nok at nævne de to mest slående eksempler - kromatografi og spektroskopi. Den anden egenskab, der er iboende i et eksperiment i analytisk kemi, er multikanal. Moderne analytisk udstyr måler samtidig signaler for mange kanaler. For eksempel måles intensiteten af ​​lystransmission for flere bølgelængder på én gang, dvs. rækkevidde. Derfor beskæftiger vi os i forsøget med mange signaler x 1 , x 2 ,...., x n, der karakteriserer sættet af koncentrationer C 1 , C 2 , ..., C m af stoffer til stede i det undersøgte system.

Ris. 1 spektre

Så et analytisk eksperiment er karakteriseret ved linearitet og multidimensionalitet. Derfor er det praktisk at betragte eksperimentelle data som vektorer og matricer og manipulere dem ved hjælp af matrixalgebra-apparatet. Frugtbarheden af ​​denne tilgang er illustreret af eksemplet vist i, som præsenterer tre spektre taget ved 200 bølgelængder fra 4000 til 4796 cm −1. Først ( x 1) og anden ( x 2) spektrene blev opnået for standardprøver, hvor koncentrationerne af to stoffer A og B er kendt: i den første prøve [A] = 0,5, [B] = 0,1, og i den anden prøve [A] = 0,2, [ B] = 0,6. Hvad kan man sige om en ny, ukendt prøve, hvis spektrum er angivet x 3 ?

Lad os overveje tre eksperimentelle spektre x 1 , x 2 og x 3 som tre vektorer af dimension 200. Ved hjælp af lineær algebra kan man nemt vise det x 3 = 0.1 x 1 +0.3 x 2, så den tredje prøve indeholder åbenbart kun stofferne A og B i koncentrationer [A] = 0,5×0,1 + 0,2×0,3 = 0,11 og [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Grundlæggende information

1.1 Matricer

Matrix kaldet en rektangulær tabel med tal, for eksempel

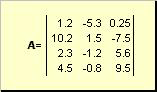
Ris. 2 Matrix

Matricer er angivet med store fed bogstaver ( EN), og deres elementer - ved tilsvarende små bogstaver med indeks, dvs. -en ij. Det første indeks nummererer rækkerne, og det andet - kolonnerne. I kemometri er det sædvanligt at angive den maksimale værdi af et indeks med samme bogstav som selve indekset, men med store bogstaver. Derfor matrixen EN kan også skrives som ( -en ij , jeg = 1,..., jeg; j = 1,..., J). For eksempel matrix jeg = 4, J= 3 og -en 23 = −7.5.

Et par tal jeg Og J kaldes matricens dimension og betegnes som jeg× J. Et eksempel på en matrix i kemometri er et sæt spektre opnået for jeg prøver til J bølgelængder.

1.2. De enkleste operationer med matricer

Matricer kan være gange med tal. I dette tilfælde ganges hvert element med dette tal. For eksempel -

Ris. 3 Multiplicer en matrix med et tal

To matricer af samme dimension kan være element for element folde Og trække fra. For eksempel,

Ris. 4 Matrix addition

Som et resultat af multiplikation med et tal og addition opnås en matrix af samme dimension.

En nulmatrix er en matrix bestående af nuller. Det er udpeget O. Det er indlysende EN+O = EN, EN−EN = O og 0 EN = O.

Matrixen kan være omsætte. Under denne operation vendes matrixen, dvs. rækker og kolonner ombyttes. Transposition er angivet med et primtal, EN" eller indeks EN t. Således, hvis EN = {-en ij , jeg = 1,..., jeg; j = 1,...,J), At EN t = ( -en ji , j = 1,...,J; i = 1,..., jeg). For eksempel

Ris. 5 Matrix transponering

Det er tydeligt at ( EN t) t = EN, (EN+B)t = A t+ B t.

1.3. Matrix multiplikation

Matricer kan være formere sig, men kun hvis de har de passende dimensioner. Hvorfor det er sådan, vil fremgå af definitionen. Matrix produkt EN, dimension jeg× K og matricer B, dimension K× J, kaldes en matrix C, dimension jeg× J, hvis elementer er tal

Altså for produktet AB det er nødvendigt, at antallet af kolonner i venstre matrix EN var lig med antallet af rækker i den højre matrix B. Et eksempel på et matrixprodukt -

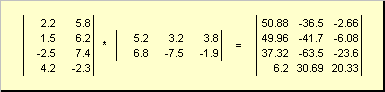
Fig.6 Produkt af matricer

Reglen for matrixmultiplikation kan formuleres som følger. For at finde et matrixelement C, stående i krydset jeg-th linje og j kolonne ( c ij) skal ganges element for element jeg-th række af den første matrix EN på j kolonne i den anden matrix B og lægge alle resultater sammen. Så i det viste eksempel opnås et element fra den tredje række og den anden kolonne som summen af ​​de elementmæssige produkter i den tredje række EN og anden kolonne B

Fig.7 Element af produktet af matricer

Produktet af matricer afhænger af rækkefølgen, dvs. AB ≠ B.A., i det mindste af dimensionelle årsager. De siger, at det er ikke-kommutativt. Produktet af matricer er dog associativt. Det betyder at ABC = (AB)C = EN(B.C.). Derudover er den også distributiv, dvs. EN(B+C) = AB+A.C.. Det er indlysende A.O. = O.

1.4. Firkantede matricer

Hvis antallet af matrixkolonner er lig med antallet af dens rækker ( jeg = J=N), så kaldes en sådan matrix kvadratisk. I dette afsnit vil vi kun overveje sådanne matricer. Blandt disse matricer kan der skelnes mellem matricer med særlige egenskaber.

Enkelt matrix (betegnet JEG, og nogle gange E) er en matrix, hvor alle elementer er lig med nul, med undtagelse af diagonale, som er lig med 1, dvs.

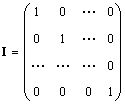
Naturligvis A.I. = I.A. = EN.

Matrixen kaldes diagonal, hvis alle dens elementer undtagen diagonale ( -en ii) er lig med nul. For eksempel

Ris. 8 Diagonal matrix

Matrix EN kaldet toppen trekantet, hvis alle dens elementer, der ligger under diagonalen, er lig med nul, dvs. -en ij= 0, kl jeg>j. For eksempel

Ris. 9 Øvre trekantet matrix

Den nederste trekantede matrix er defineret på samme måde.

Matrix EN hedder symmetrisk, hvis EN t = EN. Med andre ord -en ij = -en ji. For eksempel

Ris. 10 Symmetrisk matrix

Matrix EN hedder ortogonal, hvis

EN t EN = A.A. t = jeg.

Matrixen kaldes normal Hvis

1.5. Spor og determinant

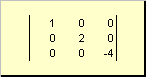
Næste kvadratisk matrix EN(angivet med Tr( EN) eller Sp( EN)) er summen af ​​dets diagonale elementer,

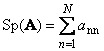
For eksempel,

Ris. 11 Matrixsporing

Det er indlysende

Sp(α EN) = α Sp( EN) Og

Sp( EN+B) = Sp( EN)+ Sp( B).

Det kan man vise

Sp( EN) = Sp( EN t), Sp( jeg) = N,

og også det

Sp( AB) = Sp( B.A.).

En anden vigtig egenskab ved en kvadratisk matrix er dens determinant(betegnet det( EN)). Det er ret vanskeligt at bestemme determinanten i det generelle tilfælde, så vi starter med den enkleste mulighed - matrixen EN dimension (2×2). Derefter

For en (3×3) matrix vil determinanten være lig med

I tilfælde af matrix ( N× N) determinanten beregnes som summen 1·2·3· ... · N= N! vilkår, som hver er ens

Indekser k 1 , k 2 ,..., k N defineres som alle mulige ordnede permutationer r tal i sættet (1, 2, ..., N). Beregning af determinanten for en matrix er en kompleks procedure, som i praksis udføres ved hjælp af specielle programmer. For eksempel,

Ris. 12 Matrix-determinant

Lad os kun bemærke de åbenlyse egenskaber:

det( jeg) = 1, det( EN) = det( EN t),

det( AB) = det( EN)det( B).

1.6. Vektorer

Hvis matricen kun består af én kolonne ( J= 1), så kaldes et sådant objekt vektor. Mere præcist, en kolonnevektor. For eksempel

Man kan også overveje matricer bestående af f.eks. én række

Dette objekt er også en vektor, men række vektor. Når man analyserer data, er det vigtigt at forstå, hvilke vektorer vi har med at gøre – kolonner eller rækker. Så spektret taget for en prøve kan betragtes som en rækkevektor. Derefter skal sættet af spektrale intensiteter ved en bestemt bølgelængde for alle prøver behandles som en kolonnevektor.

Dimensionen af ​​en vektor er antallet af dens elementer.

Det er klart, at enhver kolonnevektor kan omdannes til en rækkevektor ved transposition, dvs.

I tilfælde, hvor formen af ​​vektoren ikke er specifikt specificeret, men blot siges at være en vektor, så betyder de en kolonnevektor. Vi vil også overholde denne regel. En vektor er angivet med et lille, opretstående, fed bogstav. En nulvektor er en vektor, hvis elementer alle er nul. Det er udpeget 0 .

1.7. De enkleste operationer med vektorer

Vektorer kan tilføjes og ganges med tal på samme måde som matricer. For eksempel,

Ris. 13 Operationer med vektorer

To vektorer x Og y hedder kolineær, hvis der er et tal α sådan, at

1.8. Produkter af vektorer

To vektorer af samme dimension N kan ganges. Lad der være to vektorer x = (x 1 , x 2 ,...,x N)t og y = (y 1 , y 2 ,...,y N) t. Styret af række-for-kolonne multiplikationsreglen kan vi sammensætte to produkter ud fra dem: x t y Og xy t. Første arbejde

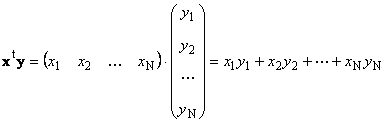
hedder skalar eller indre. Resultatet er et tal. Det er også betegnet med ( x,y)= x t y. For eksempel,

Ris. 14 Indre (skalær) produkt

Andet stykke

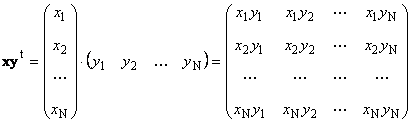
hedder ydre. Resultatet er en dimensionsmatrix ( N× N). For eksempel,

Ris. 15 Eksternt arbejde

Vektorer, hvis skalarprodukt er nul, kaldes ortogonal.

1.9. Vektor norm

Det skalære produkt af en vektor med sig selv kaldes et skalært kvadrat. denne værdi

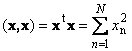
definerer en firkant længde vektor x. For at angive længde (også kaldet normen vektor) bruges notationen

For eksempel,

Ris. 16 Vektornorm

Længdeenhedsvektor (|| x|| = 1) kaldes normaliseret. Ikke-nul vektor ( x ≠ 0 ) kan normaliseres ved at dividere den med længden, dvs. x = ||x|| (x/||x||) = ||x|| e. Her e = x/||x|| - normaliseret vektor.

Vektorer kaldes ortonormale, hvis de alle er normaliserede og parvis ortogonale.

1.10. Vinkel mellem vektorer

Det skalære produkt bestemmer og hjørneφ mellem to vektorer x Og y

Hvis vektorerne er ortogonale, så er cosφ = 0 og φ = π/2, og hvis de er kolineære, så er cosφ = 1 og φ = 0.

1.11. Vektorgengivelse af en matrix

Hver matrix EN størrelse jeg× J kan repræsenteres som et sæt af vektorer

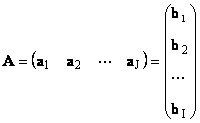
Her hver vektor -en j er j kolonne og rækkevektoren b jeg er jeg række af matricen EN

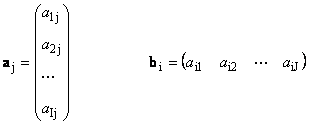
1.12. Lineært afhængige vektorer

Vektorer af samme dimension ( N) kan lægges sammen og ganges med et tal, ligesom matricer. Resultatet vil være en vektor af samme dimension. Lad der være flere vektorer af samme dimension x 1 , x 2 ,...,x K og det samme antal tal α α 1 , α 2 ,...,α K. Vektor

y= α 1 x 1 + α 2 x 2 +...+ a K x K

hedder lineær kombination vektorer x k .

Hvis der er sådanne ikke-nul tal α k ≠ 0, k = 1,..., K, Hvad y = 0 , så et sådant sæt vektorer x k hedder lineært afhængig. Ellers siges vektorerne at være lineært uafhængige. For eksempel vektorer x 1 = (2, 2)t og x 2 = (−1, −1) t er lineært afhængige, fordi x 1 +2x 2 = 0

1.13. Matrix rang

Overvej et sæt af K vektorer x 1 , x 2 ,...,x K dimensioner N. Rangen af ​​dette vektorsystem er det maksimale antal lineært uafhængige vektorer. For eksempel i sættet

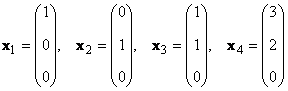
der er kun to lineært uafhængige vektorer, for eksempel x 1 og x 2, så dens rang er 2.

Det er klart, hvis der er flere vektorer i et sæt end deres dimension ( K>N), så er de nødvendigvis lineært afhængige.

Matrix rang(angivet med rang( EN)) er rangen af ​​det system af vektorer, som det består af. Selvom enhver matrix kan repræsenteres på to måder (kolonne- eller rækkevektorer), påvirker dette ikke rangværdien, fordi

1.14. omvendt matrix

Firkantet matrix EN kaldes ikke-degenereret, hvis den har en unik baglæns matrix EN-1, bestemt af forholdene

A.A. −1 = EN −1 EN = jeg.

Den inverse matrix findes ikke for alle matricer. En nødvendig og tilstrækkelig betingelse for ikke-degeneration er

det( EN) ≠ 0 eller rang( EN) = N.

Matrixinversion er en kompleks procedure, som der er specielle programmer til. For eksempel,

Ris. 17 Matrix inversion

Lad os præsentere formlerne for det enkleste tilfælde - en 2×2 matrix

Hvis matricer EN Og B er altså ikke-degenererede

(AB) −1 = B −1 EN −1 .

1.15. Pseudoinvers matrix

Hvis matrix EN er ental og den omvendte matrix eksisterer ikke, så kan du i nogle tilfælde bruge pseudo-omvendt matrix, der er defineret som en sådan matrix EN+ det

A.A. + EN = EN.

Den pseudoinverse matrix er ikke den eneste, og dens form afhænger af konstruktionsmetoden. For en rektangulær matrix kan du for eksempel bruge Moore-Penrose-metoden.

Hvis antallet af kolonner er mindre end antallet af rækker, så

EN + =(EN t EN) −1 EN t

For eksempel,

Ris. 17a Pseudo-inversion af en matrix

Hvis antallet af kolonner er større end antallet af rækker, så

EN + =EN t( A.A. t) −1

1.16. Multiplicer en vektor med en matrix

Vektor x kan ganges med en matrix EN passende størrelse. I dette tilfælde ganges kolonnevektoren til højre Økse, og vektorrækken er til venstre x t EN. Hvis vektordimensionen J, og matrixdimensionen jeg× J så vil resultatet være en vektor af dimension jeg. For eksempel,

Ris. 18 Multiplicering af en vektor med en matrix

Hvis matrix EN- firkantet ( jeg× jeg), derefter vektoren y = Økse har samme dimension som x. Det er indlysende

EN(α 1 x 1 + α 2 x 2) = α 1 Økse 1 + α 2 Økse 2 .

Derfor kan matricer betragtes som lineære transformationer af vektorer. I særdeleshed Ix = x, Okse = 0 .

2. Yderligere oplysninger

2.1. Systemer af lineære ligninger

Lade EN- matrix størrelse jeg× J, A b- dimensionsvektor J. Overvej ligningen

Økse = b

i forhold til vektoren x, dimensioner jeg. Grundlæggende er det et system af jeg lineære ligninger med J ukendt x 1 ,...,x J. En løsning findes hvis og kun hvis

rang( EN) = rang( B) = R,

Hvor B er en udvidet matrix af dimensioner jeg×( J+1), bestående af en matrix EN, suppleret med en kolonne b, B = (EN b). Ellers er ligningerne inkonsistente.

Hvis R = jeg = J, så er løsningen unik

x = EN −1 b.

Hvis R < jeg, så er der mange forskellige løsninger, der kan udtrykkes gennem en lineær kombination J−R vektorer. System af homogene ligninger Økse = 0 med kvadratisk matrix EN (N× N) har en ikke-triviel løsning ( x ≠ 0 ) hvis og kun hvis det( EN) = 0. Hvis R= rang( EN)<N, så er der N−R lineært uafhængige løsninger.

2.2. Bilineære og kvadratiske former

Hvis EN er en kvadratisk matrix, og x Og y- vektor af den tilsvarende dimension, derefter skalarproduktet af formen x t Ja hedder bilineær form defineret af matrix EN. På x = y udtryk x t Økse hedder kvadratisk form.

2.3. Positive bestemte matricer

Firkantet matrix EN hedder positiv bestemt, hvis for en hvilken som helst ikke-nul vektor x ≠ 0 ,

x t Økse > 0.

Tilsvarende defineret negativ (x t Økse < 0), ikke-negativ (x t Økse≥ 0) og negativ (x t Økse≤ 0) visse matricer.

2.4. Kolesky nedbrydning

Hvis den symmetriske matrix EN er positiv bestemt, så er der en unik trekantet matrix U med positive elementer, for hvilke

EN = U t U.

For eksempel,

Ris. 19 Kolesky nedbrydning

2.5. Polar nedbrydning

Lade EN er en ikke-singular kvadratisk matrix af dimension N× N. Så er der en unik polar ydeevne

EN = S.R.

Hvor S er en ikke-negativ symmetrisk matrix, og R er en ortogonal matrix. Matricer S Og R kan defineres eksplicit:

S 2 = A.A. t eller S = (A.A. t) ½ og R = S −1 EN = (A.A. t) −½ EN.

For eksempel,

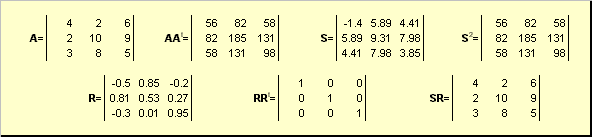
Ris. 20 Polar nedbrydning

Hvis matrix EN er degenereret, så er nedbrydningen ikke unik - nemlig: S stadig alene, men R måske meget. Polær nedbrydning repræsenterer matrixen EN som en kombination af kompression/forlængelse S og drej R.

2.6. Egenvektorer og egenværdier

Lade EN er en kvadratisk matrix. Vektor v hedder egenvektor matricer EN, hvis

Av = λ v,

hvor tallet λ kaldes egenværdi matricer EN. Altså den transformation, som matricen udfører EN over vektoren v, kommer ned til simpel strækning eller kompression med en koefficient λ. Egenvektoren bestemmes op til multiplikation med en konstant α ≠ 0, dvs. Hvis v er en egenvektor, så α v- også en egenvektor.

2.7. Egenværdier

Ved matrixen EN, dimension ( N× N) kan ikke være mere end N egenværdier. De tilfredsstiller karakteristisk ligning

det( EN − λ jeg) = 0,

som er en algebraisk ligning N- orden. Især for en 2×2 matrix har den karakteristiske ligning formen

For eksempel,

Ris. 21 Egenværdier

Sæt af egenværdier λ 1 ,..., λ N matricer EN hedder spektrum EN.

Spektret har forskellige egenskaber. I særdeleshed

det( EN) = λ 1 × ... × λ N,Sp( EN) = λ1 +...+λ N.

Egenværdierne af en vilkårlig matrix kan være komplekse tal, men hvis matrixen er symmetrisk ( EN t = EN), så er dens egenværdier reelle.

2.8. Egenvektorer

Ved matrixen EN, dimension ( N× N) kan ikke være mere end N egenvektorer, som hver svarer til deres egen værdi. For at bestemme egenvektoren v n behov for at løse et system af homogene ligninger

(EN − λ n jeg)v n = 0 .

Det har en ikke-triviel løsning, da det( A -λ n jeg) = 0.

For eksempel,

Ris. 22 egenvektorer

Egenvektorerne for en symmetrisk matrix er ortogonale.