Find egenværdier og egenvektorer af matrixeksempler. Karakteristisk ligning for en matrix
SYSTEM AF HOMOGENE LINEÆRE LIGNINGER
Et system af homogene lineære ligninger er et formsystem
Det er klart, at i dette tilfælde ![]() , fordi alle elementer i en af kolonnerne i disse determinanter er lig med nul.
, fordi alle elementer i en af kolonnerne i disse determinanter er lig med nul.
Da de ukendte findes i henhold til formlerne ![]() , så i det tilfælde, hvor Δ ≠ 0, har systemet en unik nulløsning x = y = z= 0. Men i mange problemer er det interessante spørgsmål, om et homogent system har andre løsninger end nul.
, så i det tilfælde, hvor Δ ≠ 0, har systemet en unik nulløsning x = y = z= 0. Men i mange problemer er det interessante spørgsmål, om et homogent system har andre løsninger end nul.
Sætning. For at et system af lineære homogene ligninger skal have en løsning, der ikke er nul, er det nødvendigt og tilstrækkeligt, at Δ ≠ 0.
Så hvis determinanten Δ ≠ 0, så har systemet en unik løsning. Hvis Δ ≠ 0, så har systemet af lineære homogene ligninger et uendeligt antal løsninger.
Eksempler.

Egenvektorer og egenværdier af en matrix
Lad en kvadratisk matrix gives  , x– en matrix-søjle, hvis højde falder sammen med rækkefølgen af matrixen EN. .
, x– en matrix-søjle, hvis højde falder sammen med rækkefølgen af matrixen EN. .
I mange problemer skal vi overveje ligningen for x
hvor λ er et bestemt tal. Det er klart, at for enhver λ har denne ligning en nulløsning.
Tallet λ, som denne ligning har løsninger, der ikke er nul, kaldes egenværdi matricer EN, A x thi sådan kaldes λ egenvektor matricer EN.
Lad os finde egenvektoren for matricen EN. Fordi E∙X = X, så kan matrixligningen omskrives som ![]() eller
eller ![]() . I udvidet form kan denne ligning omskrives som et system af lineære ligninger. Virkelig
. I udvidet form kan denne ligning omskrives som et system af lineære ligninger. Virkelig  .
.
Og derfor 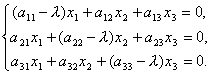
Så vi har fået et system af homogene lineære ligninger til bestemmelse af koordinaterne x 1, x 2, x 3 vektor x. For at et system skal have ikke-nul-løsninger er det nødvendigt og tilstrækkeligt, at systemets determinant er lig med nul, dvs.

Dette er en 3. grads ligning for λ. Det hedder karakteristisk ligning matricer EN og tjener til at bestemme egenværdierne af λ.
Hver egenværdi λ svarer til en egenvektor x, hvis koordinater er bestemt ud fra systemet ved den tilsvarende værdi af λ.
Eksempler.
VEKTORALGEBRA. KONCEPTET VEKTOR
Når man studerer forskellige grene af fysik, er der mængder, der er fuldstændigt bestemt ved at specificere deres numeriske værdier, for eksempel længde, areal, masse, temperatur osv. Sådanne mængder kaldes skalære. Men ud over dem er der også mængder, for at bestemme hvilke, ud over den numeriske værdi, det også er nødvendigt at kende deres retning i rummet, for eksempel kraften, der virker på kroppen, hastigheden og accelerationen af krop, når den bevæger sig i rummet, magnetfeltstyrken på et givet punkt i rummet og osv. Sådanne mængder kaldes vektormængder.
Lad os introducere en streng definition.
Instrueret segment Lad os kalde et segment, i forhold til hvis ender det er kendt, hvilken af dem der er den første og hvilken der er den anden.

Vektor kaldes et rettet segment med en vis længde, dvs. Dette er et segment af en vis længde, hvor et af punkterne, der begrænser det, tages som begyndelsen, og det andet som slutningen. Hvis EN– begyndelsen af vektoren, B er dens ende, så er vektoren angivet med symbolet; desuden er vektoren ofte angivet med et enkelt bogstav. På figuren er vektoren angivet med et segment, og dens retning med en pil.
modul eller længde En vektor kaldes længden af det rettede segment, der definerer den. Benævnt med || eller ||.
Vi vil også inkludere den såkaldte nulvektor, hvis begyndelse og slutning falder sammen, som vektorer. Det er udpeget. Nulvektoren har ikke en bestemt retning, og dens modul er nul ||=0.
Vektorer kaldes collineær, hvis de er placeret på samme linje eller på parallelle linjer. Desuden, hvis vektorerne og er i samme retning, vil vi skrive , modsat.
Vektorer placeret på lige linjer parallelt med samme plan kaldes koplanar.
De to vektorer kaldes lige, hvis de er collineære, har samme retning og er lige lange. I dette tilfælde skriver de.
Af definitionen af lighed af vektorer følger det, at en vektor kan transporteres parallelt med sig selv og placere dens oprindelse på ethvert punkt i rummet.
For eksempel .
LINEÆRE OPERATIONER PÅ VEKTORER
Produktet af en vektor og tallet λ er en ny vektor, således at:
Produktet af en vektor og et tal λ er angivet med .

For eksempel er der en vektor rettet i samme retning som vektoren og med en længde, der er halvt så stor som vektoren.
Den indførte operation har følgende egenskaber:
Lad og være to vilkårlige vektorer. Lad os tage et vilkårligt punkt O og konstruer en vektor. Efter det fra punktet EN lad os lægge vektoren til side. Vektoren, der forbinder begyndelsen af den første vektor med slutningen af den anden, kaldes beløb af disse vektorer og er betegnet ![]() .
.

Den formulerede definition af vektoraddition kaldes parallelogram regel, da den samme sum af vektorer kan opnås som følger. Lad os udsætte fra punktet O vektorer og . Lad os konstruere et parallelogram på disse vektorer OABC. Siden vektorer, så vektor, som er en diagonal af et parallelogram tegnet fra toppunktet O, vil naturligvis være en sum af vektorer.
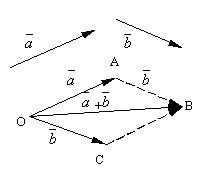
Det er nemt at kontrollere følgende egenskaber ved vektoraddition.
En vektor kollineær til en given vektor, lige lang og modsat rettet, kaldes modsat vektor for en vektor og er betegnet med . Den modsatte vektor kan betragtes som resultatet af at gange vektoren med tallet λ = –1: .
Hvordan indsætter man matematiske formler på en hjemmeside?
Hvis du nogensinde har brug for at tilføje en eller to matematiske formler til en webside, så er den nemmeste måde at gøre dette på som beskrevet i artiklen: matematiske formler indsættes nemt på webstedet i form af billeder, der automatisk genereres af Wolfram Alpha . Ud over enkelhed vil denne universelle metode hjælpe med at forbedre webstedets synlighed i søgemaskiner. Det har virket i lang tid (og, tror jeg, vil virke for evigt), men er allerede moralsk forældet.
Hvis du jævnligt bruger matematiske formler på dit websted, så anbefaler jeg, at du bruger MathJax - et særligt JavaScript-bibliotek, der viser matematisk notation i webbrowsere, der bruger MathML, LaTeX eller ASCIIMathML markup.
Der er to måder at begynde at bruge MathJax på: (1) ved hjælp af en simpel kode, kan du hurtigt forbinde et MathJax script til dit websted, som automatisk indlæses fra en ekstern server på det rigtige tidspunkt (liste over servere); (2) download MathJax-scriptet fra en fjernserver til din server og tilslut det til alle sider på dit websted. Den anden metode - mere kompleks og tidskrævende - vil fremskynde indlæsningen af dit websteds sider, og hvis den overordnede MathJax-server bliver midlertidigt utilgængelig af en eller anden grund, vil dette ikke påvirke dit eget websted på nogen måde. På trods af disse fordele valgte jeg den første metode, da den er enklere, hurtigere og ikke kræver tekniske færdigheder. Følg mit eksempel, og på kun 5 minutter vil du være i stand til at bruge alle funktionerne i MathJax på dit websted.
Du kan forbinde MathJax-biblioteksscriptet fra en ekstern server ved hjælp af to kodemuligheder taget fra MathJax hovedwebsted eller på dokumentationssiden:
En af disse kodemuligheder skal kopieres og indsættes i koden på din webside, helst mellem tags og eller umiddelbart efter tagget. Ifølge den første mulighed indlæses MathJax hurtigere og sænker siden mindre. Men den anden mulighed overvåger og indlæser automatisk de nyeste versioner af MathJax. Hvis du indsætter den første kode, skal den opdateres med jævne mellemrum. Hvis du indsætter den anden kode, indlæses siderne langsommere, men du behøver ikke konstant at overvåge MathJax-opdateringer.
Den nemmeste måde at forbinde MathJax på er i Blogger eller WordPress: Tilføj en widget, der er designet til at indsætte tredjeparts JavaScript-kode i webstedets kontrolpanel, kopier den første eller anden version af downloadkoden præsenteret ovenfor ind i den, og placer widgetten tættere på til begyndelsen af skabelonen (det er i øvrigt slet ikke nødvendigt, da MathJax-scriptet indlæses asynkront). Det er alt. Lær nu markup-syntaksen for MathML, LaTeX og ASCIIMathML, og du er klar til at indsætte matematiske formler på dit websteds websider.
Enhver fraktal er konstrueret efter en bestemt regel, som konsekvent anvendes et ubegrænset antal gange. Hver sådan tid kaldes en iteration.
Den iterative algoritme til at konstruere en Menger-svamp er ret enkel: den originale terning med side 1 er opdelt af planer parallelt med dens flader i 27 lige store terninger. En central terning og 6 terninger støder op til den langs fladerne fjernes fra den. Resultatet er et sæt bestående af de resterende 20 mindre terninger. Gør vi det samme med hver af disse terninger, får vi et sæt bestående af 400 mindre terninger. Hvis vi fortsætter denne proces i det uendelige, får vi en Menger-svamp.
En egenvektor for en kvadratisk matrix er en, der, når den ganges med en given matrix, resulterer i en kollineær vektor. Med enkle ord, når en matrix multipliceres med en egenvektor, forbliver sidstnævnte den samme, men multipliceret med et vist tal.
DefinitionEn egenvektor er en ikke-nul vektor V, som, når den multipliceres med en kvadratisk matrix M, selv bliver forøget med et eller andet tal λ. I algebraisk notation ser det sådan ud:
M × V = λ × V,
hvor λ er egenværdien af matrixen M.
Lad os se på et numerisk eksempel. For at lette optagelsen vil tal i matrixen blive adskilt af et semikolon. Lad os have en matrix:
- M = 0; 4;
- 6; 10.
Lad os gange det med en kolonnevektor:
- V = -2;
Når vi multiplicerer en matrix med en kolonnevektor, får vi også en kolonnevektor. I strengt matematisk sprog vil formlen for at multiplicere en 2 × 2 matrix med en kolonnevektor se sådan ud:
- M × V = M11 × V11 + M12 × V21;
- M21 × V11 + M22 × V21.
M11 betyder elementet i matrix M placeret i første række og første kolonne, og M22 betyder elementet placeret i anden række og anden kolonne. For vores matrix er disse elementer lig med M11 = 0, M12 = 4, M21 = 6, M22 10. For en kolonnevektor er disse værdier lig med V11 = –2, V21 = 1. Ifølge denne formel, vi får følgende resultat af produktet af en kvadratisk matrix med en vektor:
- M × V = 0 × (-2) + (4) × (1) = 4;
- 6 × (-2) + 10 × (1) = -2.
Lad os for nemheds skyld skrive kolonnevektoren i en række. Så vi multiplicerede den kvadratiske matrix med vektoren (-2; 1), hvilket resulterede i vektoren (4; -2). Det er klart, at dette er den samme vektor ganget med λ = -2. Lambda i dette tilfælde angiver egenværdien af matricen.
En egenvektor til en matrix er en kollineær vektor, det vil sige et objekt, der ikke ændrer sin position i rummet, når det multipliceres med en matrix. Begrebet kollinearitet i vektoralgebra ligner udtrykket parallelisme i geometri. I en geometrisk fortolkning er kollineære vektorer parallelt rettede segmenter af forskellig længde. Siden Euklids tid ved vi, at en linje har et uendeligt antal linjer parallelle med sig, så det er logisk at antage, at hver matrix har et uendeligt antal egenvektorer.
Fra det foregående eksempel er det klart, at egenvektorer kan være (-8; 4), og (16; -8) og (32, -16). Disse er alle kollineære vektorer svarende til egenværdien λ = -2. Når vi multiplicerer den oprindelige matrix med disse vektorer, vil vi stadig ende med en vektor, der adskiller sig fra originalen med 2 gange. Det er derfor, når man løser problemer med at finde en egenvektor, er det nødvendigt kun at finde lineært uafhængige vektorobjekter. Oftest er der for en n × n matrix et n antal egenvektorer. Vores lommeregner er designet til analyse af andenordens kvadratmatricer, så næsten altid vil resultatet finde to egenvektorer, bortset fra tilfælde hvor de falder sammen.
I eksemplet ovenfor kendte vi egenvektoren for den oprindelige matrix på forhånd og bestemte tydeligt lambdatallet. Men i praksis sker alt omvendt: egenværdierne findes først og først derefter egenvektorerne.
LøsningsalgoritmeLad os se på den oprindelige matrix M igen og prøve at finde begge dens egenvektorer. Så matricen ser sådan ud:
- M = 0; 4;
- 6; 10.
Først skal vi bestemme egenværdien λ, som kræver beregning af determinanten af følgende matrix:
- (0 - λ); 4;
- 6; (10 - λ).
Denne matrix opnås ved at trække den ukendte λ fra elementerne på hoveddiagonalen. Determinanten bestemmes ved hjælp af standardformlen:
- detA = M11 × M21 − M12 × M22
- detA = (0 − λ) × (10 − λ) − 24
Da vores vektor skal være ikke-nul, accepterer vi den resulterende ligning som lineært afhængig og sidestiller vores determinant detA til nul.
(0 − λ) × (10 − λ) − 24 = 0
Lad os åbne parenteserne og få den karakteristiske ligning for matricen:
λ 2 − 10λ − 24 = 0
Dette er en standard andengradsligning, der skal løses ved hjælp af en diskriminant.
D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196
Roden af diskriminanten er sqrt(D) = 14, derfor λ1 = -2, λ2 = 12. For hver lambda-værdi skal vi nu finde egenvektoren. Lad os udtrykke systemkoefficienterne for λ = -2.
- M - λ × E = 2; 4;
- 6; 12.
I denne formel er E identitetsmatrixen. Baseret på den resulterende matrix skaber vi et system af lineære ligninger:
2x + 4y = 6x + 12y,
hvor x og y er egenvektorelementerne.
Lad os samle alle X'erne til venstre og alle Y'erne til højre. Det er klart - 4x = 8y. Divider udtrykket med - 4 og få x = –2y. Nu kan vi bestemme den første egenvektor af matricen ved at tage alle værdier af de ukendte (husk uendeligheden af lineært afhængige egenvektorer). Lad os tage y = 1, så x = –2. Derfor ser den første egenvektor ud som V1 = (–2; 1). Vend tilbage til begyndelsen af artiklen. Det var dette vektorobjekt, vi gangede matricen med for at demonstrere begrebet en egenvektor.
Lad os nu finde egenvektoren for λ = 12.
- M - X x E = -12; 4
- 6; -2.
Lad os skabe det samme system af lineære ligninger;
- -12x + 4y = 6x - 2y
- -18x = -6 år
- 3x = y.
Nu tager vi x = 1, derfor y = 3. Den anden egenvektor ser således ud som V2 = (1; 3). Når man multiplicerer den oprindelige matrix med en given vektor, vil resultatet altid være den samme vektor ganget med 12. Det er her løsningsalgoritmen slutter. Nu ved du, hvordan man manuelt bestemmer egenvektoren for en matrix.
- determinant;
- spor, det vil sige summen af elementerne på hoveddiagonalen;
- rang, det vil sige det maksimale antal lineært uafhængige rækker/kolonner.
Programmet fungerer i henhold til ovenstående algoritme, hvilket forkorter løsningsprocessen så meget som muligt. Det er vigtigt at påpege, at i programmet er lambda betegnet med bogstavet "c". Lad os se på et numerisk eksempel.
Eksempel på hvordan programmet fungererLad os prøve at bestemme egenvektorerne for følgende matrix:
- M = 5; 13;
- 4; 14.
Lad os indtaste disse værdier i cellerne i lommeregneren og få svaret i følgende form:
- Matrix rang: 2;
- Matrixdeterminant: 18;
- Matrix-spor: 19;
- Beregning af egenvektoren: c 2 − 19,00c + 18,00 (karakteristisk ligning);
- Egenvektorberegning: 18 (første lambdaværdi);
- Egenvektorberegning: 1 (anden lambdaværdi);
- Ligningssystem for vektor 1: -13x1 + 13y1 = 4x1 − 4y1;
- Ligningssystem for vektor 2: 4x1 + 13y1 = 4x1 + 13y1;
- Egenvektor 1: (1; 1);
- Egenvektor 2: (-3,25; 1).
Således opnåede vi to lineært uafhængige egenvektorer.
KonklusionLineær algebra og analytisk geometri er standardfag for enhver nyuddannet ingeniørstuderende. Det store antal vektorer og matricer er skræmmende, og det er nemt at lave fejl i så besværlige beregninger. Vores program vil give eleverne mulighed for at kontrollere deres beregninger eller automatisk løse problemet med at finde en egenvektor. Der er andre lineære algebra-beregnere i vores katalog; brug dem i dine studier eller arbejde.
Med matrix A, hvis der er et tal l, således at AX = lX.
I dette tilfælde kaldes tallet l for egenværdien af operatoren (matrix A), svarende til vektoren X.
Med andre ord er en egenvektor en vektor, der under påvirkning af en lineær operator transformerer til en kollineær vektor, dvs. bare gange med et eller andet tal. I modsætning hertil er ukorrekte vektorer mere komplekse at transformere.
Lad os nedskrive definitionen af en egenvektor i form af et ligningssystem:
Lad os flytte alle udtryk til venstre side:

Sidstnævnte system kan skrives i matrixform som følger:
(A - lE)X = O
Det resulterende system har altid en nulløsning X = O. Sådanne systemer, hvor alle frie led er lig med nul, kaldes homogene. Hvis matrixen af et sådant system er firkantet, og dets determinant ikke er lig med nul, vil vi ved hjælp af Cramers formler altid få en unik løsning - nul. Det kan bevises, at et system har ikke-nul løsninger, hvis og kun hvis determinanten af denne matrix er lig med nul, dvs.
|A - lE| =  = 0
= 0
Denne ligning med ukendt l kaldes den karakteristiske ligning (karakteristisk polynomium) for matricen A (lineær operator).
Det kan bevises, at det karakteristiske polynomium for en lineær operator ikke afhænger af valget af grundlag.
Lad os for eksempel finde egenværdierne og egenvektorerne for den lineære operator defineret af matrixen A = .
For at gøre dette, lad os oprette en karakteristisk ligning |A - lE| = ![]() = (1 - 1) 2 - 36 = 1 - 2l + 12 - 36 = 12 - 21 - 35 = 0; D = 4 + 140 = 144; egenværdier l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12)/2 = 7.
= (1 - 1) 2 - 36 = 1 - 2l + 12 - 36 = 12 - 21 - 35 = 0; D = 4 + 140 = 144; egenværdier l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12)/2 = 7.
For at finde egenvektorer løser vi to ligningssystemer
(A + 5E)X = O
(A - 7E)X = O
For den første af dem tager den udvidede matrix formen
![]() ,
,
hvorfra x 2 = c, x 1 + (2/3) c = 0; x 1 = -(2/3)s, dvs. X (1) = (-(2/3)s; s).
For den anden af dem tager den udvidede matrix formen
![]() ,
,
hvorfra x2 = c1, xl - (2/3)c1 = 0; x 1 = (2/3)s 1, dvs. X (2) = ((2/3)s 1; s 1).
Egenvektorerne for denne lineære operator er således alle vektorer af formen (-(2/3)с; с) med egenværdi (-5) og alle vektorer af formen ((2/3)с 1 ; с 1) med egenværdi 7 .
Det kan bevises, at matrixen for operatoren A i grundlaget bestående af dens egenvektorer er diagonal og har formen:
 ,
,
hvor l i er egenværdierne af denne matrix.
Det omvendte er også sandt: hvis matrix A i en eller anden basis er diagonal, så vil alle vektorer af denne basis være egenvektorer af denne matrix.
Det kan også bevises, at hvis en lineær operator har n parvis distinkte egenværdier, så er de tilsvarende egenvektorer lineært uafhængige, og matrixen af denne operator i den tilsvarende basis har en diagonal form.
Lad os illustrere dette med det foregående eksempel. Lad os tage vilkårlige ikke-nul værdier c og c 1, men sådan at vektorerne X (1) og X (2) er lineært uafhængige, dvs. ville danne grundlag. Lad f.eks. c = c 1 = 3, så X (1) = (-2; 3), X (2) = (2; 3).
Lad os verificere den lineære uafhængighed af disse vektorer:
12 ≠ 0. I dette nye grundlag vil matrix A have formen A * = .
For at bekræfte dette, lad os bruge formlen A * = C -1 AC. Lad os først finde C -1.
C-1 = ![]() ;
;

Den kvadratiske form f(x 1, x 2, x n) af n variable er en sum, hvis led er enten kvadratet af en af variablerne eller produktet af to forskellige variable taget med en bestemt koefficient: f( x 1, x 2, x n ) = ![]() (a ij = en ji).
(a ij = en ji).
Matrix A, der er sammensat af disse koefficienter, kaldes en matrix af kvadratisk form. Dette er altid en symmetrisk matrix (dvs. en matrix symmetrisk omkring hoveddiagonalen, a ij = en ji).
I matrixnotation er den kvadratiske form f(X) = X T AX, hvor
Ja

Lad os for eksempel skrive den kvadratiske form på matrixform.
For at gøre dette finder vi en matrix af kvadratisk form. Dens diagonale elementer er lig med koefficienterne for de kvadratiske variable, og de resterende elementer er lig med halvdelene af de tilsvarende koefficienter i den kvadratiske form. Derfor

Lad matrixkolonnen af variable X opnås ved en ikke-degenereret lineær transformation af matrixkolonnen Y, dvs. X = CY, hvor C er en ikke-singular matrix af n. orden. Så den andengradsform f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.
Således, med en ikke-degenereret lineær transformation C, antager matrixen af kvadratisk form formen: A * = C T AC.
Lad os for eksempel finde den kvadratiske form f(y 1, y 2), opnået fra den kvadratiske form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 ved lineær transformation.

En andengradsform kaldes kanonisk (har en kanonisk form), hvis alle dens koefficienter a ij = 0 for i ≠ j, dvs.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.
Dens matrix er diagonal.
Sætning (bevis ikke givet her). Enhver kvadratisk form kan reduceres til kanonisk form ved hjælp af en ikke-degenereret lineær transformation.
Lad os for eksempel reducere den kvadratiske form til kanonisk form
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.
For at gøre dette skal du først vælge et komplet kvadrat med variablen x 1:
f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.
Nu vælger vi et komplet kvadrat med variablen x 2:
f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 - 5(x 2 2 + 2* x 2 *(1/10)x 3 + (1/100)x 3 2) + (5/100)x 3 2 =
= 2(x 1 + x 2) 2 - 5(x 2 - (1/10) x 3) 2 + (1/20) x 3 2.
Så bringer den ikke-degenererede lineære transformation y 1 = x 1 + x 2, y 2 = x 2 + (1/10)x 3 og y 3 = x 3 denne kvadratiske form til den kanoniske form f(y 1, y 2 , y 3) = 2y 1 2 - 5y 2 2 + (1/20) y 3 2 .
Bemærk, at den kanoniske form af en andengradsform er bestemt tvetydigt (den samme andengradsform kan reduceres til kanonisk form på forskellige måder). Men kanoniske former opnået ved forskellige metoder har en række fælles egenskaber. Især afhænger antallet af led med positive (negative) koefficienter af en kvadratisk form ikke af metoden til at reducere formen til denne form (for eksempel vil der i det betragtede eksempel altid være to negative og en positiv koefficient). Denne egenskab kaldes inertiloven for kvadratiske former.
Lad os bekræfte dette ved at bringe den samme kvadratiske form til kanonisk form på en anden måde. Lad os starte transformationen med variablen x 2:
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2+
+ 2* x 2 ((1/6) x 3 - (2/3)x 1) + ((1/6) x 3 - (2/3)x 1) 2) + 3((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
= -3(x 2 + (1/6) x 3 - (2/3)x 1) 2 + 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (y 1 , y 2 , y 3) = -3y 1 2 -
+3y 2 2 + 2y 3 2, hvor y 1 = - (2/3)x 1 + x 2 + (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 og y3 = x1. Her er der en negativ koefficient -3 ved y 1 og to positive koefficienter 3 og 2 ved y 2 og y 3 (og ved hjælp af en anden metode fik vi en negativ koefficient (-5) ved y 2 og to positive: 2 ved y 1 og 1/20 ved y 3).
Det skal også bemærkes, at rangordenen af en matrix af en kvadratisk form, kaldet rangen af den kvadratiske form, er lig med antallet af ikke-nul koefficienter for den kanoniske form og ændres ikke under lineære transformationer.
En andengradsform f(X) kaldes positiv (negativ) bestemt, hvis den for alle værdier af variablerne, der ikke samtidigt er lig med nul, er positiv, dvs. f(X) > 0 (negativ, dvs.
f(X)< 0).
F.eks. er andengradsformen f 1 (X) = x 1 2 + x 2 2 positiv bestemt, fordi er en sum af kvadrater, og andengradsformen f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 er negativ bestemt, fordi repræsenterer det kan repræsenteres som f 2 (X) = -(x 1 - x 2) 2.
I de fleste praktiske situationer er det noget sværere at fastslå det bestemte tegn på en kvadratisk form, så til dette bruger vi en af følgende sætninger (vi vil formulere dem uden bevis).
Sætning. En kvadratisk form er positiv (negativ) bestemt, hvis og kun hvis alle egenværdier af dens matrix er positive (negative).
Sætning (Sylvesters kriterium). En andengradsform er positiv bestemt, hvis og kun hvis alle de førende mol i denne forms matrix er positive.
Den primære (kantede) mol af k. orden af n. ordens matrix A er determinanten for matricen, der er sammensat af de første k rækker og kolonner i matrixen A ().
Bemærk, at for negative definitive kvadratiske former veksler fortegnene for de primære mindreårige, og den første ordens mol skal være negativ.
Lad os for eksempel undersøge den kvadratiske form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 for tegnbestemthed.
![]() = (2 - l)*
= (2 - l)*
*(3 - 1) - 4 = (6 - 2 1 - 3 1 + 1 2) - 4 = 1 2 - 5 1 + 2 = 0; D = 25-8 = 17; ![]() . Derfor er den kvadratiske form positiv bestemt.
. Derfor er den kvadratiske form positiv bestemt.
Metode 2. Principal mol af første orden af matrix A D 1 = a 11 = 2 > 0. Principal mol af anden orden D 2 = = 6 - 4 = 2 > 0. Derfor er den kvadratiske form ifølge Sylvesters kriterium positiv bestemt.
Vi undersøger en anden kvadratisk form for tegnbestemthed, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.
Metode 1. Lad os konstruere en matrix med kvadratisk form A = . Den karakteristiske ligning vil have formen ![]() = (-2 - l)*
= (-2 - l)*
*(-3 - 1) - 4 = (6 + 2 1 + 3 1 + 1 2) - 4 = 1 2 + 5 1 + 2 = 0; D = 25-8 = 17; ![]() . Derfor er den kvadratiske form negativ bestemt.
. Derfor er den kvadratiske form negativ bestemt.
Metode 2. Principal minor af første orden af matrix A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. I henhold til Sylvesters kriterium er den kvadratiske form følgelig negativ bestemt (fortegnene for de primære minorer veksler, begyndende med minus).
Og som et andet eksempel undersøger vi den fortegnsbestemte kvadratiske form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2.
Metode 1. Lad os konstruere en matrix med kvadratisk form A = . Den karakteristiske ligning vil have formen ![]() = (2 - l)*
= (2 - l)*
*(-3 - 1) - 4 = (-6 - 2 1 + 3 1 + 1 2) - 4 = 12 + 1 - 10 = 0; D = 1 + 40 = 41; ![]() .
.
Et af disse tal er negativt, og det andet er positivt. Tegnene for egenværdierne er forskellige. Følgelig kan den kvadratiske form hverken være negativt eller positivt bestemt, dvs. denne kvadratiske form er ikke tegnbestemt (den kan tage værdier af ethvert tegn).
Metode 2. Principal mol af første orden af matrix A D 1 = a 11 = 2 > 0. Principal mol af anden orden D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).
