Matriisin suurin ominaisarvo. Matriisin ominaisyhtälö

Diagonaalityyppiset matriisit järjestetään yksinkertaisimmin. Herää kysymys, onko mahdollista löytää kanta, jossa lineaarioperaattorin matriisilla olisi diagonaalinen muoto. Tällainen perusta on olemassa.
Olkoon lineaarinen avaruus R n ja siinä toimiva lineaarinen operaattori A; tässä tapauksessa operaattori A ottaa R n itseensä, eli A:R n → R n .

Määritelmä. Nollasta poikkeavaa vektoria kutsutaan operaattorin A ominaisvektoriksi, jos operaattori A muuttuu sille kollineaariseksi vektoriksi, eli . Lukua λ kutsutaan ominaisvektoria vastaavan operaattorin A ominaisarvoksi tai ominaisarvoksi.
Huomaamme joitain ominaisarvojen ja ominaisvektorien ominaisuuksia.
1. Mikä tahansa ominaisvektorien lineaarinen yhdistelmä Samaa ominaisarvoa λ vastaavan operaattorin A ominaisuusvektori on sama ominaisarvo.
2. Ominaisvektorit Operaattori A, jolla on pareittain erilliset ominaisarvot λ 1 , λ 2 , …, λ m, ovat lineaarisesti riippumattomia.
3. Jos ominaisarvot λ 1 =λ 2 = λ m = λ, niin ominaisarvo λ vastaa enintään m lineaarisesti riippumatonta ominaisvektoria.

Eli jos on n lineaarisesti riippumatonta ominaisvektoria jotka vastaavat erilaisia ​​ominaisarvoja λ 1 , λ 2 , …, λ n , niin ne ovat lineaarisesti riippumattomia, joten ne voidaan ottaa avaruuden R n perustaksi. Etsitään lineaarisen operaattorin A matriisin muoto sen ominaisvektorien perusteella, jolle toimimme operaattorin A kanssa kantavektoreiden perusteella: Sitten .
Siten lineaarioperaattorin A matriisilla sen ominaisvektorien perusteella on diagonaalimuoto ja operaattorin A ominaisarvot ovat diagonaalissa.
Onko olemassa muuta perustaa, jossa matriisilla on diagonaalinen muoto? Vastaus tähän kysymykseen saadaan seuraavalla lauseella.

Lause. Lineaarisen operaattorin A matriisilla kannassa (i = 1..n) on diagonaalimuoto silloin ja vain, jos kaikki kannan vektorit ovat operaattorin A ominaisvektoreita.

Sääntö ominaisarvojen ja ominaisvektorien löytämiseksi

. (*)

(1)
Missä on lineaarisen operaattorin matriisi.

Järjestelmällä (1) on nollasta poikkeava ratkaisu, jos sen determinantti D on nolla

Esimerkki 12. Lineaarinen operaattori A toimii R 3:ssa lain mukaan, missä x 1 , x 2 , .., x n ovat kantavektorin koordinaatit , , . Etsi tämän operaattorin ominaisarvot ja ominaisvektorit.
Ratkaisu. Rakennamme tämän operaattorin matriisin:
.
Luomme järjestelmän ominaisvektorien koordinaattien määrittämiseksi:

Muodostamme ominaisyhtälön ja ratkaisemme sen:

.
λ 1,2 = -1, λ 3 = 3.
Korvaamalla λ = -1 järjestelmään, meillä on:
tai
Koska , silloin on kaksi riippuvaa muuttujaa ja yksi vapaa muuttuja.
Olkoon siis x 1 vapaa tuntematon Ratkaisemme tämän järjestelmän millä tahansa tavalla ja löydämme tämän järjestelmän yleisen ratkaisun: Ratkaisujen perusjärjestelmä koostuu yhdestä ratkaisusta, koska n - r = 3 - 2 = 1.
Ominaisarvoa λ = -1 vastaavalla ominaisvektorijoukolla on muoto: , jossa x 1 on mikä tahansa muu luku kuin nolla. Valitaan yksi vektori tästä joukosta esimerkiksi asettamalla x 1 = 1: .
Väittelemällä samalla tavalla, löydämme ominaisarvoa λ = 3 vastaavan ominaisvektorin: .
Avaruudessa R3 kanta koostuu kolmesta lineaarisesti riippumattomasta vektorista, mutta olemme saaneet vain kaksi lineaarisesti riippumatonta ominaisvektoria, joista ei voida muodostaa kantaa R3:ssa. Näin ollen lineaarioperaattorin matriisia A ei voida pelkistää diagonaalimuotoon.

Esimerkki 13 Annettu matriisi .
1. Todista, että vektori on matriisin A ominaisvektori. Etsi tätä ominaisvektoria vastaava ominaisarvo.
2. Etsi kanta, jossa matriisilla A on diagonaalinen muoto.
Ratkaisu.
1. Jos , niin on ominaisvektori

.
Vektori (1, 8, -1) on ominaisvektori. Ominaisarvo λ = -1.
Matriisin kantassa on diagonaalimuoto, joka koostuu ominaisvektoreista. Yksi heistä on kuuluisa. Etsitään loput.
Etsimme ominaisvektoreita järjestelmästä:

Ominaisuusyhtälö: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Etsi ominaisarvoa λ = -3 vastaava ominaisvektori:

Tämän järjestelmän matriisin arvo on kaksi ja se on yhtä suuri kuin tuntemattomien lukumäärä, joten tällä järjestelmällä on vain nollaratkaisu x 1 = x 3 = 0. x 2 voi tässä olla mitä tahansa muuta kuin nolla, esim. x 2 = 1. Siten vektori (0 ,1,0) on ominaisvektori, joka vastaa arvoa λ = -3. Tarkistetaan:
.
Jos λ = 1, niin saamme järjestelmän
Matriisin sijoitus on kaksi. Yliviivaa viimeinen yhtälö.
Olkoon x 3 vapaa tuntematon. Sitten x 1 \u003d -3x 3, 4x 2 = 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 = 9x 3.
Olettaen, että x 3 = 1, meillä on (-3,-9,1) - ominaisarvoa λ = 1 vastaava ominaisvektori. Tarkista:

.
Koska ominaisarvot ovat todellisia ja erilaisia, niitä vastaavat vektorit ovat lineaarisesti riippumattomia, joten ne voidaan ottaa R3:n perustaksi. Perusteessa siis , , matriisilla A on muoto:
.
Lineaarisen operaattorin A:R n → R n jokaista matriisia ei voida pelkistää diagonaalimuotoon, koska joillakin lineaarisilla operaattoreilla voi olla vähemmän kuin n lineaarisesti riippumatonta ominaisvektoria. Kuitenkin, jos matriisi on symmetrinen, täsmälleen m lineaarisesti riippumatonta vektoria vastaa multiplisisuuden m ominaisyhtälön juuria.

Määritelmä. Symmetrinen matriisi on neliömatriisi, jossa päälävistäjän suhteen symmetriset alkiot ovat yhtä suuret, eli jossa .
Huomautukset. 1. Kaikki symmetrisen matriisin ominaisarvot ovat todellisia.
2. Pareittain eri ominaisarvoja vastaavan symmetrisen matriisin ominaisvektorit ovat ortogonaalisia.
Yhtenä tutkitun laitteen lukuisista sovelluksista tarkastelemme ongelmaa toisen asteen käyrän muodon määrittämisessä.

Määritelmä 9.3. Vektori X nimeltään oma vektori matriiseja A jos sellainen numero on λ, että tasa-arvo pätee: A X= λ X, eli hakemisen tulos X matriisin antama lineaarinen muunnos A, on tämän vektorin kertolasku luvulla λ . Itse numero λ nimeltään oma numero matriiseja A.

Korvaus kaavoiksi (9.3) x` j = λx j , saamme yhtälöjärjestelmän ominaisvektorin koordinaattien määrittämiseksi:

. (9.5)

Tällä lineaarisella homogeenisella järjestelmällä on ei-triviaali ratkaisu vain, jos sen päädeterminantti on 0 (Cramerin sääntö). Kirjoittamalla tämä ehto muodossa:

saamme yhtälön ominaisarvojen määrittämiseksi λ nimeltään ominaisyhtälö. Lyhyesti sanottuna se voidaan esittää seuraavasti:

| A-λE | = 0, (9.6)

koska sen vasen puoli on matriisin determinantti A-λE. Polynomi suhteessa λ | A-λE| nimeltään ominaispolynomi matriisit a.

Karakterisen polynomin ominaisuudet:

1) Lineaarimuunnoksen karakteristinen polynomi ei riipu kannan valinnasta. Todiste. (katso (9.4)), mutta siis,. Ei siis riipu perusteen valinnasta. Siksi ja | A-λE| ei muutu uudelle perustalle siirryttäessä.

2) Jos matriisi A lineaarinen muunnos on symmetrinen(nuo. a ij = a ji), silloin kaikki ominaisyhtälön (9.6) juuret ovat reaalilukuja.

Ominaisarvojen ja ominaisvektorien ominaisuudet:

1) Jos valitsemme kantan ominaisvektoreista x 1, x 2, x 3 jotka vastaavat ominaisarvoja λ1, λ2, λ3 matriiseja A, niin tällä perusteella lineaarisella muunnoksella A on diagonaalimatriisi:

(9.7) Tämän ominaisuuden todiste seuraa ominaisvektorien määritelmästä.

2) Jos muunnos ominaisarvot A ovat erilaisia, silloin niitä vastaavat ominaisvektorit ovat lineaarisesti riippumattomia.

3) Jos matriisin ominaispolynomi A on kolme eri juuria, sitten jollain perusteella matriisi A on diagonaalinen muoto.

Etsitään matriisin ominaisarvot ja ominaisvektorit. Tehdään ominaisyhtälö: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Etsi kutakin löydettyä arvoa vastaavien ominaisvektorien koordinaatit λ. (9.5):stä seuraa, että jos X (1) ={x 1, x 2, x 3) on ominaisvektori, joka vastaa λ 1 = -2 siis

on yhteinen, mutta määrittelemätön järjestelmä. Sen ratkaisu voidaan kirjoittaa muodossa X (1) ={a,0,-a), jossa a on mikä tahansa luku. Erityisesti, jos tarvitset sitä | x (1) |=1, X (1) =

Korvaaminen järjestelmään (9.5) λ 2 =3, saadaan järjestelmä toisen ominaisvektorin koordinaattien määrittämiseksi - x (2) ={y1,y2,y3}:

, missä X (2) ={b,-b,b) tai jos | x (2) |=1, x (2) =

varten λ 3 = 6 etsi ominaisvektori x (3) ={z1, z2, z3}:

, x (3) ={c,2c, c) tai normalisoidussa versiossa

x (3) = Sen voi nähdä X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = eKr- 2bc + bc= 0. Tämän matriisin ominaisvektorit ovat siis pareittain ortogonaalisia.

Luento 10

Neliömuodot ja niiden yhteys symmetrisiin matriiseihin. Symmetrisen matriisin ominaisvektorien ja ominaisarvojen ominaisuudet. Neliöllisen muodon pelkistys kanoniseen muotoon.

Määritelmä 10.1.neliömuoto todellisia muuttujia x 1, x 2,…, x n kutsutaan näiden muuttujien suhteen toisen asteen polynomia, joka ei sisällä vapaata termiä ja ensimmäisen asteen termejä.

Esimerkkejä kvadraattisista muodoista:

(n = 2),

(n = 3). (10.1)

Muista viime luennossa annettu symmetrisen matriisin määritelmä:

Määritelmä 10.2. Neliömatriisia kutsutaan symmetrinen, jos , eli jos päälävistäjän suhteen symmetriset matriisielementit ovat yhtä suuret.

Symmetrisen matriisin ominaisarvojen ja ominaisvektorien ominaisuudet:

1) Kaikki symmetrisen matriisin ominaisarvot ovat todellisia.

Todiste (for n = 2).

Anna matriisin A näyttää: . Tehdään ominaisyhtälö:

(10.2) Etsi diskriminantti:

Siksi yhtälöllä on vain todelliset juuret.

2) Symmetrisen matriisin ominaisvektorit ovat ortogonaalisia.

Todiste (for n= 2).

Ominaisuusvektorien koordinaattien ja on täytettävä yhtälöt.

HOMOGEENISTEN LINEAARISET YHTÄLÖJÄRJESTELMÄ

Homogeenisten lineaaristen yhtälöiden järjestelmä on muotoinen järjestelmä

On selvää, että tässä tapauksessa , koska näiden determinanttien yhden sarakkeen kaikki elementit ovat yhtä suuria kuin nolla.

Koska tuntemattomat löydetään kaavoilla , silloin kun Δ ≠ 0, järjestelmällä on ainutlaatuinen nollaratkaisu x = y = z= 0. Monissa ongelmissa kiinnostaa kuitenkin kysymys siitä, onko homogeenisella järjestelmällä muita ratkaisuja kuin nolla.

Lause. Jotta lineaaristen homogeenisten yhtälöiden ratkaisulla olisi nollasta poikkeava ratkaisu, on välttämätöntä ja riittävää, että Δ ≠ 0.

Joten jos determinantti on Δ ≠ 0, niin järjestelmällä on ainutlaatuinen ratkaisu. Jos Δ ≠ 0, niin lineaarisilla homogeenisilla yhtälöillä on ääretön määrä ratkaisuja.

Esimerkkejä.

Ominaisvektorit ja matriisin ominaisarvot

Olkoon neliömatriisi annettu , X on jokin matriisisarake, jonka korkeus on sama kuin matriisin järjestys A. .

Monissa ongelmissa on otettava huomioon yhtälö for X

missä λ on jokin luku. On selvää, että millä tahansa λ:lla tällä yhtälöllä on nollaratkaisu.

Kutsutaan lukua λ, jolle tällä yhtälöllä on nollasta poikkeavat ratkaisut ominaisarvo matriiseja A, A X tällaista λ:ta kutsutaan oma vektori matriiseja A.

Etsitään matriisin ominaisvektori A. Koska E∙X = X, niin matriisiyhtälö voidaan kirjoittaa uudelleen muotoon tai . Laajennetussa muodossa tämä yhtälö voidaan kirjoittaa uudelleen lineaaristen yhtälöiden järjestelmäksi. Todella .

Ja siksi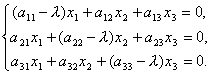

Joten saimme homogeenisten lineaaristen yhtälöiden järjestelmän koordinaattien määrittämiseksi x 1, x2, x 3 vektori X. Jotta järjestelmässä olisi nollasta poikkeavia ratkaisuja, on välttämätöntä ja riittävää, että järjestelmän determinantti on yhtä suuri kuin nolla, ts.

Tämä on 3. asteen yhtälö suhteessa λ. Sitä kutsutaan ominaisyhtälö matriiseja A ja sen avulla määritetään ominaisarvot λ.

Jokainen ominaisarvo λ vastaa ominaisvektoria X, jonka koordinaatit määritetään järjestelmästä vastaavalla λ:n arvolla.

Esimerkkejä.

VEKTORIN ALGEBRA. VEKTORIN KONSEPTI

Fysiikan eri aloja tutkiessa on suureita, jotka määritetään kokonaan asettamalla niiden numeeriset arvot, esimerkiksi pituus, pinta-ala, massa, lämpötila jne. Tällaisia ​​arvoja kutsutaan skalaariksi. Niiden lisäksi on kuitenkin myös suureita, joiden määrittämiseen tarvitaan numeerisen arvon lisäksi myös niiden suunta avaruudessa, esimerkiksi kehoon vaikuttava voima, nopeus ja kiihtyvyys. kehosta sen liikkuessa avaruudessa, magneettikentän voimakkuutta tietyssä avaruuden pisteessä jne. Tällaisia ​​suureita kutsutaan vektorisuureiksi.

Otetaan käyttöön tiukka määritelmä.

Suunnattu segmentti Kutsutaan segmentti, jonka päihin nähden tiedetään, mikä niistä on ensimmäinen ja mikä toinen.

Vektori kutsutaan suunnattua segmenttiä, jolla on tietty pituus, ts. Tämä on tietyn pituinen segmentti, jossa yksi sitä rajoittavista pisteistä otetaan alkuna ja toinen - lopuksi. Jos A on vektorin alku, B on sen loppu, silloin vektoria merkitään symbolilla, lisäksi vektoria merkitään usein yhdellä kirjaimella . Kuvassa vektori on merkitty segmentillä ja sen suunta nuolella.

moduuli tai pitkä vektoria kutsutaan sen määrittävän suunnatun segmentin pituudeksi. Merkitään || tai ||.

Niin kutsuttua nollavektoria, jonka alku ja loppu ovat samat, kutsutaan myös vektoreiksi. Se on merkitty. Nollavektorilla ei ole tarkkaa suuntaa ja sen moduuli on yhtä suuri kuin nolla ||=0.

Vektoreita ja kutsutaan kollineaarinen jos ne sijaitsevat samalla linjalla tai rinnakkaisilla linjoilla. Tässä tapauksessa, jos vektorit ja ovat yhtä suunnattuja, kirjoitamme , päinvastoin.

Kutsutaan vektoreita, jotka sijaitsevat saman tason suuntaisilla suorilla koplanaarinen.

Kaksi vektoria ja kutsutaan yhtä suuri jos ne ovat kollineaarisia, niillä on sama suunta ja ne ovat yhtä pitkiä. Kirjoita tässä tapauksessa.

Vektorien yhtäläisyyden määritelmästä seuraa, että vektoria voidaan siirtää yhdensuuntaisesti itsensä kanssa asettamalla sen origo mihin tahansa avaruuden pisteeseen.

Esimerkiksi.

LINEAARISET OPERATIOT VEKTOREILLA

1. Vektorin kertominen luvulla.

   Vektorin tulo luvulla λ on uusi vektori, joka:

   Vektorin ja luvun λ tuloa merkitään .

   

   Esimerkiksi, on vektori, joka osoittaa samaan suuntaan kuin vektori ja jonka pituus on puolet vektorin pituudesta.

   Syötetyllä toiminnolla on seuraava ominaisuuksia:

2. Vektorien lisäys.

   Olkoon ja kaksi mielivaltaista vektoria. Ota mielivaltainen kohta O ja rakentaa vektori . Sen jälkeen pisteestä A syrjään vektori . Kutsutaan vektoria, joka yhdistää ensimmäisen vektorin alun toisen loppuun summa näistä vektoreista ja on merkitty .

   

   Muotoiltua vektorinlisäyksen määritelmää kutsutaan suunnikassääntö, koska sama vektorien summa voidaan saada seuraavasti. Siirrä sivuun pisteestä O vektorit ja . Muodosta suunnikas näille vektoreille OABC. Koska vektorit , niin sitten vektori , joka on kärjestä vedetyn suunnikkaan diagonaali O, on ilmeisesti vektorien summa .

   

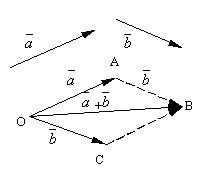
   Seuraavat asiat on helppo tarkistaa vektorin lisäysominaisuudet.

3. Vektorien ero.

   Kutsutaan vektoria, joka on kollineaarinen tietylle vektorille, yhtä pitkä ja vastakkaiseen suuntaan vastapäätä vektori vektorille ja sitä merkitään . Vastakkaista vektoria voidaan pitää tuloksena kertomalla vektori luvulla λ = –1: .

Neliomatriisin ominaisvektori on sellainen, joka kerrottuna annetulla matriisilla johtaa kollineaariseen vektoriin. Yksinkertaisesti sanottuna, kun matriisi kerrotaan ominaisvektorilla, jälkimmäinen pysyy samana, mutta kerrotaan jollakin numerolla.

Määritelmä

Ominaisuusvektori on nollasta poikkeava vektori V, joka neliömatriisilla M kerrottuna muuttuu omaksi itsekseen lisättynä jollain luvulla λ. Algebrallisessa merkinnässä tämä näyttää tältä:

M × V = λ × V,

missä λ on matriisin M ominaisarvo.

Tarkastellaanpa numeerista esimerkkiä. Kirjoittamisen helpottamiseksi matriisin numerot erotetaan puolipisteellä. Oletetaan, että meillä on matriisi:

• M = 0; 4;
• 6; 10.

Kerrotaan se sarakevektorilla:

• V = -2;

Kun matriisi kerrotaan sarakevektorilla, saadaan myös sarakevektori. Tiukassa matemaattisessa kielessä kaava 2 × 2 -matriisin kertomiseksi sarakevektorilla näyttäisi tältä:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 tarkoittaa matriisin M elementtiä, joka on ensimmäisellä rivillä ja ensimmäisessä sarakkeessa, ja M22 on toisella rivillä ja toisessa sarakkeessa olevaa elementtiä. Matriisissamme nämä alkiot ovat M11 = 0, M12 = 4, M21 = 6, M22 10. Sarakevektorille nämä arvot ovat V11 = –2, V21 = 1. Tämän kaavan mukaan saamme seuraavan tulos neliömatriisin tulosta vektorilla:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Mukavuuden vuoksi kirjoitamme sarakevektorin riville. Joten olemme kertoneet neliömatriisin vektorilla (-2; 1), jolloin tuloksena on vektori (4; -2). Ilmeisesti tämä on sama vektori kerrottuna λ = -2:lla. Lambda tarkoittaa tässä tapauksessa matriisin ominaisarvoa.

Matriisin ominaisvektori on kollineaarinen vektori, eli esine, joka ei muuta sijaintiaan avaruudessa, kun se kerrotaan matriisilla. Kollineaarisuuden käsite vektorialgebrassa on samanlainen kuin geometrian yhdensuuntaisuuden termi. Geometrisessä tulkinnassa kollineaariset vektorit ovat samansuuntaisia ​​eripituisia segmenttejä. Eukleideen ajoista lähtien tiedämme, että yhdellä suoralla on ääretön määrä sen rinnalla olevia viivoja, joten on loogista olettaa, että jokaisella matriisilla on ääretön määrä ominaisvektoreita.

Edellisestä esimerkistä voidaan nähdä, että sekä (-8; 4) että (16; -8) ja (32, -16) voivat olla ominaisvektoreita. Kaikki nämä ovat kollineaarisia vektoreita, jotka vastaavat ominaisarvoa λ = -2. Kerrottaessa alkuperäinen matriisi näillä vektoreilla, saadaan tuloksena silti vektori, joka eroaa alkuperäisestä 2 kertaa. Tästä syystä ominaisvektorin löytämisen ongelmia ratkaistaessa vaaditaan vain lineaarisesti riippumattomien vektoriobjektien löytäminen. Useimmiten n × n -matriisilla on n:s määrä ominaisvektoreita. Laskimemme on suunniteltu toisen kertaluvun neliömatriisien analysointiin, joten tuloksena löytyy lähes aina kaksi ominaisvektoria, paitsi jos ne ovat yhteneväisiä.

Yllä olevassa esimerkissä tiesimme etukäteen alkuperäisen matriisin ominaisvektorin ja määritimme visuaalisesti lambda-luvun. Käytännössä kaikki tapahtuu kuitenkin päinvastoin: alussa on ominaisarvot ja vasta sitten ominaisvektorit.

Ratkaisualgoritmi

Katsotaanpa alkuperäistä matriisia M uudelleen ja yritetään löytää sen molemmat ominaisvektorit. Joten matriisi näyttää tältä:

• M = 0; 4;
• 6; 10.

Aluksi meidän on määritettävä ominaisarvo λ, jolle meidän on laskettava seuraavan matriisin determinantti:

• (0 - λ); 4;
• 6; (10 − λ).

Tämä matriisi saadaan vähentämällä tuntematon λ päädiagonaalin elementeistä. Determinantti määritetään vakiokaavalla:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Koska vektorimme ei saa olla nolla, pidämme tuloksena olevaa yhtälöä lineaarisesti riippuvaisena ja yhtälömme determinanttimme detA nollaan.

(0 − λ) × (10 − λ) − 24 = 0

Avataan sulut ja saadaan matriisin ominaisyhtälö:

λ 2 − 10 λ − 24 = 0

Tämä on tavallinen toisen asteen yhtälö, joka on ratkaistava erottimen suhteen.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Diskriminantin juuri on sqrt(D) = 14, joten λ1 = -2, λ2 = 12. Nyt jokaiselle lambda-arvolle on löydettävä ominaisvektori. Esitetään järjestelmän kertoimet λ = -2:lle.

• M - λ × E = 2; 4;
• 6; 12.

Tässä kaavassa E on identiteettimatriisi. Muodostamme saadun matriisin perusteella lineaarisen yhtälöjärjestelmän:

2x + 4v = 6x + 12v

missä x ja y ovat ominaisvektorin alkioita.

Keräätään kaikki X:t vasemmalta ja kaikki Y:t oikealta. Ilmeisesti - 4x = 8v. Jaa lauseke -4:llä ja saa x = -2y. Nyt voimme määrittää matriisin ensimmäisen ominaisvektorin ottamalla mitkä tahansa tuntemattomien arvot (muista lineaarisesti riippuvien ominaisvektorien ääretön). Otetaan y = 1, sitten x = -2. Siksi ensimmäinen ominaisvektori näyttää tältä V1 = (–2; 1). Palaa artikkelin alkuun. Tällä vektoriobjektilla kerroimme matriisin havainnollistaaksemme ominaisvektorin käsitteen.

Etsitään nyt ominaisvektori arvolle λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Tehdään sama lineaarinen yhtälöjärjestelmä;

• -12x + 4v = 6x -2v
• -18x = -6v
• 3x=y.

Otetaan nyt x = 1, joten y = 3. Siten toinen ominaisvektori näyttää tältä V2 = (1; 3). Kun alkuperäinen matriisi kerrotaan tällä vektorilla, tulos on aina sama vektori kerrottuna 12:lla. Tämä täydentää ratkaisualgoritmin. Nyt tiedät kuinka määritellä manuaalisesti matriisin ominaisvektori.

• determinantti;
• jäljitys, eli päälävistäjän elementtien summa;
• rank, eli lineaarisesti riippumattomien rivien/sarakkeiden enimmäismäärä.

Ohjelma toimii yllä olevan algoritmin mukaisesti minimoiden ratkaisuprosessin. On tärkeää huomauttaa, että lambda on merkitty kirjaimella "c" ohjelmassa. Katsotaanpa numeerista esimerkkiä.

Esimerkki ohjelmasta

Yritetään määritellä ominaisvektorit seuraavalle matriisille:

• M = 5; 13;
• 4; 14.

Syötetään nämä arvot laskimen soluihin ja saadaan vastaus seuraavassa muodossa:

• Matriisisijoitus: 2;
• Matriisideterminantti: 18;
• Matriisijäljitys: 19;
• Ominaisuusvektorin laskenta: c 2 − 19.00c + 18.00 (ominaisuusyhtälö);
• Omavektorilaskenta: 18 (ensimmäinen lambda-arvo);
• Omavektorilaskenta: 1 (toinen lambda-arvo);
• Vektorin 1 yhtälöjärjestelmä: -13x1 + 13y1 = 4x1 − 4y1;
• Vektorin 2 yhtälöjärjestelmä: 4x1 + 13y1 = 4x1 + 13y1;
• Ominaisuusvektori 1: (1; 1);
• Ominaisuusvektori 2: (-3,25; 1).

Siten olemme saaneet kaksi lineaarisesti riippumatonta ominaisvektoria.

Johtopäätös

Lineaarinen algebra ja analyyttinen geometria ovat vakioaineita jokaiselle tekniikan fuksille. Suuri määrä vektoreita ja matriiseja on pelottavaa, ja on helppo tehdä virhe sellaisissa hankalia laskelmissa. Ohjelmamme avulla opiskelijat voivat tarkistaa laskelmansa tai ratkaista automaattisesti ominaisvektorin löytämisen ongelman. Luettelossamme on muitakin lineaarisia algebralaskimia, käytä niitä opiskelussasi tai työssäsi.

www.sivusto antaa sinun löytää. Sivusto tekee laskelman. Muutamassa sekunnissa palvelin antaa oikean ratkaisun. Matriisin ominaisyhtälö on algebrallinen lauseke, joka löytyy determinantin laskentasäännöstä matriiseja matriiseja, kun taas päädiagonaalissa diagonaalielementtien ja muuttujan arvoissa on eroja. Laskettaessa ominaisyhtälö matriisille verkossa, jokainen elementti matriiseja kerrotaan vastaavilla muilla elementeillä matriiseja. Etsi tilassa verkossa mahdollista vain neliölle matriiseja. Etsi toiminta ominaisyhtälö matriisille verkossa pelkistyy elementtien tulon algebrallisen summan laskemiseen matriiseja determinantin löytämisen seurauksena matriiseja, vain määrittämistä varten ominaisyhtälö matriisille verkossa. Tällä operaatiolla on erityinen paikka teoriassa matriiseja, voit löytää ominaisarvoja ja vektoreita juurien avulla. Tehtävän löytäminen ominaisyhtälö matriisille verkossa on moninkertaistaa elementtejä matriiseja näiden tuotteiden myöhemmin laskemalla yhteen tietyn säännön mukaisesti. www.sivusto löytöjä matriisin ominaisyhtälö annettu mitta tilassa verkossa. laskeminen ominaisyhtälö matriisille verkossa annetulle ulottuvuudelle tämä on polynomin löytäminen numeerisilla tai symbolisilla kertoimilla, jotka löytyvät determinantin laskentasäännöstä matriiseja- vastaavien elementtien tulojen summana matriiseja, vain määrittämistä varten ominaisyhtälö matriisille verkossa. Polynomin löytäminen neliön muuttujan suhteen matriiseja, määritelmänä matriisin ominaisyhtälö, yleistä teoriassa matriiseja. Polynomin juurien arvo ominaisyhtälö matriisille verkossa käytetään ominaisvektorien ja ominaisarvojen määrittämiseen matriiseja. Kuitenkin, jos määräävä tekijä matriiseja on sitten nolla matriisin ominaisyhtälö on edelleen olemassa, toisin kuin päinvastoin matriiseja. Laskeakseen matriisin ominaisyhtälö tai etsi useita kerralla matriisien ominaisyhtälöt, sinun täytyy viettää paljon aikaa ja vaivaa, kun taas palvelimemme löytää ominaisyhtälö online-matriisille. Tässä tapauksessa vastaus etsimällä ominaisyhtälö matriisille verkossa on oikein ja riittävän tarkasti, vaikka numerot löydettäessä ominaisyhtälö matriisille verkossa tulee olemaan järjetöntä. Sivustolla www.sivusto merkkimerkinnät ovat sallittuja elementeissä matriiseja, tuo on ominaisyhtälö online-matriisille voidaan esittää yleisessä symbolisessa muodossa laskettaessa ominaisyhtälömatriisi verkossa. Saatu vastaus on hyödyllistä tarkistaa etsimisongelmaa ratkaistaessa ominaisyhtälö matriisille verkossa käyttämällä sivustoa www.sivusto. Suorittaessasi polynomin laskentatoimintoa - matriisin ominaisyhtälö, sinun on oltava tarkkaavainen ja erittäin keskittynyt tämän ongelman ratkaisemisessa. Sivustomme puolestaan ​​auttaa sinua tarkistamaan päätöksesi aiheesta ominaisyhtälömatriisi verkossa. Jos sinulla ei ole aikaa ratkaistujen ongelmien pitkiin tarkastuksiin, niin www.sivusto on varmasti kätevä työkalu etsimiseen ja laskemiseen ominaisyhtälö matriisille verkossa.