ដែនកំណត់ដ៏អស្ចារ្យទីមួយ និងទីពីរ គឺជាឧទាហរណ៍នៃដំណោះស្រាយ។ ដែនកំណត់គួរឱ្យកត់សម្គាល់: ដែនកំណត់គួរឱ្យកត់សម្គាល់ទីមួយនិងទីពីរ
រូបមន្តសម្រាប់ដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរគឺ lim x → ∞ 1 + 1 x x = e ។ ទម្រង់នៃការសរសេរមួយទៀតមើលទៅដូចនេះ៖ lim x → 0 (1 + x) 1 x = e ។
នៅពេលយើងនិយាយអំពីដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ យើងត្រូវដោះស្រាយជាមួយនឹងភាពមិនច្បាស់លាស់នៃទម្រង់ 1 ∞ , i.e. ឯកតាទៅកម្រិតគ្មានកំណត់។
Yandex.RTB R-A-339285-1
ពិចារណាបញ្ហាដែលយើងត្រូវការសមត្ថភាពក្នុងការគណនាដែនកំណត់ដ៏អស្ចារ្យទីពីរ។
ឧទាហរណ៍ ១
រកដែនកំណត់ lim x → ∞ 1 − 2 x 2 + 1 x 2 + 1 4 ។
ដំណោះស្រាយ
ជំនួសរូបមន្តដែលចង់បានហើយអនុវត្តការគណនា។
lim x → ∞ 1 − 2 x 2 + 1 x 2 + 1 4 = 1 − 2 ∞ 2 + 1 ∞ 2 + 1 4 = 1 − 0 ∞ = 1 ∞
នៅក្នុងចម្លើយរបស់យើង យើងទទួលបានឯកតាមួយចំពោះថាមពលនៃភាពគ្មានទីបញ្ចប់។ ដើម្បីកំណត់វិធីសាស្រ្តនៃដំណោះស្រាយ យើងប្រើតារាងនៃភាពមិនច្បាស់លាស់។ យើងជ្រើសរើសដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរហើយធ្វើការផ្លាស់ប្តូរអថេរ។
t \u003d - x 2 + 1 2 ⇔ x 2 + 1 4 \u003d - t 2
ប្រសិនបើ x → ∞ បន្ទាប់មក t → - ∞ ។
តោះមើលអ្វីដែលយើងទទួលបានបន្ទាប់ពីការជំនួស៖
lim x → ∞ 1 − 2 x 2 + 1 x 2 + 1 4 = 1 ∞ = lim x → ∞ 1 + 1 t − 1 2 t = lim t → ∞ 1 + 1 t t − 1 2 = e − 1 2
ចម្លើយ៖ lim x → ∞ 1 − 2 x 2 + 1 x 2 + 1 4 = e − 1 2 .
ឧទាហរណ៍ ២
គណនាដែនកំណត់ lim x → ∞ x − 1 x + 1 x ។
ដំណោះស្រាយ
ជំនួសភាពគ្មានទីបញ្ចប់ ហើយទទួលបានដូចខាងក្រោម។
lim x → ∞ x − 1 x + 1 x = lim x → ∞ 1 − 1 x 1 + 1 x x = 1 − 0 1 + 0 ∞ = 1 ∞
នៅក្នុងចំលើយ យើងទទួលបានដូចគ្នាម្តងទៀតនូវបញ្ហាមុន ដូច្នេះហើយ យើងអាចប្រើដែនកំណត់ដ៏អស្ចារ្យទីពីរម្តងទៀត។ បន្ទាប់យើងត្រូវជ្រើសរើសផ្នែកចំនួនគត់នៅមូលដ្ឋាននៃអនុគមន៍ថាមពល៖
x − 1 x + 1 = x + 1 − 2 x + 1 = x + 1 x + 1 − 2 x + 1 = 1 − 2 x + 1
បន្ទាប់ពីនោះ ដែនកំណត់មានទម្រង់ដូចខាងក្រោមៈ
lim x → ∞ x − 1 x + 1 x = 1 ∞ = lim x → ∞ 1 − 2 x + 1 x
យើងជំនួសអថេរ។ ចូរនិយាយថា t = − x + 1 2 ⇒ 2 t = − x − 1 ⇒ x = − 2 t − 1 ; ប្រសិនបើ x → ∞ បន្ទាប់មក t → ∞ ។
បន្ទាប់ពីនោះ យើងសរសេរនូវអ្វីដែលយើងទទួលបានក្នុងដែនកំណត់ដើម៖
lim x → ∞ x − 1 x + 1 x = 1 ∞ = lim x → ∞ 1 − 2 x + 1 x = lim x → ∞ 1 + 1 t − 2 t − 1 = = lim x → ∞ 1 + 1 t − 2 t 1 + 1 t − 1 = lim x → ∞ 1 + 1 t − 2 t lim x → ∞ 1 + 1 t − 1 = = lim x → ∞ 1 + 1 t t − 2 1 + 1 ∞ = e − 2 (1 + 0) − 1 = អ៊ី − 2
ដើម្បីអនុវត្តការបំប្លែងនេះ យើងបានប្រើលក្ខណៈសម្បត្តិជាមូលដ្ឋាននៃដែនកំណត់ និងអំណាច។
ចម្លើយ៖ lim x → ∞ x − 1 x + 1 x = e − 2 ។
ឧទាហរណ៍ ៣
គណនាដែនកំណត់ lim x → ∞ x 3 + 1 x 3 + 2 x 2 − 1 3 x 4 2 x 3 − 5 ។
ដំណោះស្រាយ
lim x → ∞ x 3 + 1 x 3 + 2 x 2 − 1 3 x 4 2 x 3 − 5 = lim x → ∞ 1 + 1 x 3 1 + 2 x − 1 x 3 3 2 x − 5 x 4 = = 1 + 0 1 + 0 − 0 3 0 − 0 = 1∞
បន្ទាប់ពីនោះ យើងត្រូវធ្វើការបំប្លែងមុខងារ ដើម្បីអនុវត្តដែនកំណត់ដ៏អស្ចារ្យទីពីរ។ យើងទទួលបានដូចខាងក្រោមៈ
lim x → ∞ x 3 + 1 x 3 + 2 x 2 − 1 3 x 4 2 x 3 − 5 = 1 ∞ = lim x → ∞ x 3 − 2 x 2 − 1 − 2 x 2 + 2 x 3 + 2 x 2 − 1 3 x 4 2 x 3 − 5 = = lim x → ∞ 1 + − 2 x 2 + 2 x 3 + 2 x 2 − 1 3 x 4 2 x 3 − 5
lim x → ∞ 1 + − 2 x 2 + 2 x 3 + 2 x 2 − 1 3 x 4 2 x 3 − 5 = lim x → ∞ 1 + − 2 x 2 + 2 x 3 + 2 x 2 − 1 x 3 + 2 x 2 − 1 − 2 x 2 + 2 − 2 x 2 + 2 x 3 + 2 x 2 − 1 3 x 4 2 x 3 − 5 = = lim x → ∞ 1 + − 2 x 2 + 2 x 3 + 2 x 2 − 1 x 3 + 2 x 2 − 1 − 2 x 2 + 2 − 2 x 2 + 2 x 3 + 2 x 2 − 1 3 x 4 2 x 3 − 5
ចាប់តាំងពីពេលនេះយើងមាននិទស្សន្តដូចគ្នានៅក្នុងភាគយក និងភាគបែងនៃប្រភាគ (ស្មើនឹងប្រាំមួយ) ដែនកំណត់នៃប្រភាគនៅភាពគ្មានទីបញ្ចប់នឹងស្មើនឹងសមាមាត្រនៃមេគុណទាំងនេះនៅថាមពលខ្ពស់ជាង។
lim x → ∞ 1 + − 2 x 2 + 2 x 3 + 2 x 2 − 1 x 3 + 2 x 2 − 1 − 2 x 2 + 2 − 2 x 2 + 2 x 3 + 2 x 2 − 1 3 x 4 2 x 3 − 5 = = lim x → ∞ 1 + − 2 x 2 + 2 x 3 + 2 x 2 − 1 x 3 + 2 x 2 − 1 − 2 x 2 + 2 − 6 2 = lim x → ∞ 1 + − 2 x 2 + 2 x 3 + 2 x 2 − 1 x 3 + 2 x 2 − 1 − 2 x 2 + 2 − 3
ការជំនួស t = x 2 + 2 x 2 - 1 - 2 x 2 + 2 យើងទទួលបានដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ។ មានន័យថាអ្វី៖
lim x → ∞ 1 + − 2 x 2 + 2 x 3 + 2 x 2 − 1 x 3 + 2 x 2 − 1 − 2 x 2 + 2 − 3 = lim x → ∞ 1 + 1 t t − 3 = e − ៣
ចម្លើយ៖ lim x → ∞ x 3 + 1 x 3 + 2 x 2 − 1 3 x 4 2 x 3 − 5 = e − 3 ។
ការសន្និដ្ឋាន
ភាពមិនច្បាស់លាស់ 1 ∞ , i.e. ឯកតាទៅកម្រិតគ្មានកំណត់ គឺជាភាពមិនច្បាស់លាស់នៃច្បាប់ថាមពល ដូច្នេះវាអាចត្រូវបានបង្ហាញដោយប្រើច្បាប់សម្រាប់ការស្វែងរកដែនកំណត់នៃអនុគមន៍អិចស្ប៉ូណង់ស្យែល។
ប្រសិនបើអ្នកសម្គាល់ឃើញមានកំហុសនៅក្នុងអត្ថបទ សូមបន្លិចវា ហើយចុច Ctrl+Enter
ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងត្រូវបានគេហៅថាសមភាពដូចខាងក្រោមៈ
\begin(សមីការ)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(សមីការ)
ដោយសារសម្រាប់ $\alpha\to(0)$ យើងមាន $\sin\alpha\to(0)$ យើងនិយាយថាដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងបង្ហាញពីភាពមិនច្បាស់លាស់នៃទម្រង់ $\frac(0)(0)$ ។ និយាយជាទូទៅក្នុងរូបមន្ត (1) ជំនួសឱ្យអថេរ $\alpha$ នៅក្រោមសញ្ញាស៊ីនុស និងក្នុងភាគបែង កន្សោមណាមួយអាចមានទីតាំងនៅ ដរាបណាលក្ខខណ្ឌពីរត្រូវបានបំពេញ៖
- កន្សោមនៅក្រោមសញ្ញាស៊ីនុស និងក្នុងភាគបែងក្នុងពេលដំណាលគ្នាមានទំនោរទៅសូន្យ ពោលគឺឧ។ មានភាពមិនច្បាស់លាស់នៃទម្រង់ $\frac(0)(0)$ ។
- កន្សោមនៅក្រោមសញ្ញាស៊ីនុស និងក្នុងភាគបែងគឺដូចគ្នា។
Corollaries ពីដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងក៏ត្រូវបានគេប្រើជាញឹកញាប់ផងដែរ:
\begin(សមីការ) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(សមីការ)
ឧទាហរណ៍ដប់មួយត្រូវបានដោះស្រាយនៅលើទំព័រនេះ។ ឧទាហរណ៍លេខ 1 ត្រូវបានឧទ្ទិសដល់ភស្តុតាងនៃរូបមន្ត (2)-(4) ។ ឧទាហរណ៍ #2, #3, #4 និង #5 មានដំណោះស្រាយជាមួយនឹងមតិយោបល់លម្អិត។ ឧទាហរណ៍ 6-10 មានដំណោះស្រាយជាមួយនឹងមតិយោបល់តិចតួច ឬគ្មាន ដូចដែលការពន្យល់លម្អិតត្រូវបានផ្តល់ឱ្យនៅក្នុងឧទាហរណ៍មុន។ នៅពេលដោះស្រាយ រូបមន្តត្រីកោណមាត្រមួយចំនួនត្រូវបានប្រើប្រាស់ ដែលអាចត្រូវបានរកឃើញ។
ខ្ញុំចំណាំថាវត្តមាននៃអនុគមន៍ត្រីកោណមាត្ររួមជាមួយនឹងភាពមិនច្បាស់លាស់នៃ $\frac (0) (0)$ មិនមែនមានន័យថាដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងត្រូវតែត្រូវបានអនុវត្តនោះទេ។ ពេលខ្លះការបំប្លែងត្រីកោណមាត្រសាមញ្ញគឺគ្រប់គ្រាន់ - ឧទាហរណ៍សូមមើល។
ឧទាហរណ៍ #1
បង្ហាញថា $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ ។
ក) ចាប់តាំងពី $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$ បន្ទាប់មក៖
$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$
ចាប់តាំងពី $\lim_(\alpha\to(0))\cos(0)=1$ និង $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$ , បន្ទាប់មក៖
$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0))) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$
ខ) ចូរធ្វើការជំនួស $\alpha=\sin(y)$ ។ ចាប់តាំងពី $\sin(0)=0$ បន្ទាប់មកពីលក្ខខណ្ឌ $\alpha\to(0)$ យើងមាន $y\to(0)$ ។ លើសពីនេះទៀត មានសង្កាត់នៃសូន្យ ដែល $\arcsin\alpha=\arcsin(\sin(y))=y$ ដូច្នេះ៖
$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y)))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1)=1. $$
សមភាព $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ ត្រូវបានបញ្ជាក់។
គ) ចូរធ្វើការជំនួស $\alpha=\tg(y)$ ។ ចាប់តាំងពី $\tg(0)=0$ លក្ខខណ្ឌ $\alpha\to(0)$ និង $y\to(0)$ គឺសមមូល។ លើសពីនេះទៀត មានសង្កាត់នៃលេខសូន្យ ដែល $\arctg\alpha=\arctg\tg(y))=y$ ដូច្នេះដោយពឹងផ្អែកលើលទ្ធផលនៃចំនុច a) យើងនឹងមាន៖
$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y)))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1)=1. $$
សមភាព $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ ត្រូវបានបញ្ជាក់។
ភាពស្មើគ្នា ក) ខ) គ) ជាញឹកញាប់ត្រូវបានគេប្រើរួមជាមួយនឹងដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។
ឧទាហរណ៍ #2
ដែនកំណត់គណនា $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)( x+7))$ ។
ចាប់តាំងពី $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ និង $\lim_( x \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, i.e. ហើយភាគយក និងភាគបែងនៃប្រភាគក្នុងពេលដំណាលគ្នាមានទំនោរទៅសូន្យ បន្ទាប់មកនៅទីនេះយើងកំពុងដោះស្រាយជាមួយនឹងភាពមិនច្បាស់លាស់នៃទម្រង់ $\frac(0)(0)$, i.e. បានអនុវត្ត។ លើសពីនេះទៀត វាអាចត្រូវបានគេមើលឃើញថាកន្សោមនៅក្រោមសញ្ញាស៊ីនុស និងក្នុងភាគបែងគឺដូចគ្នា (ឧ. និងពេញចិត្ត)៖
ដូច្នេះ លក្ខខណ្ឌទាំងពីរដែលបានរាយនៅដើមទំព័រត្រូវបានបំពេញ។ វាធ្វើតាមពីនេះដែលរូបមន្តអាចអនុវត្តបាន i.e. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+7 ))=1$។
ចម្លើយ៖ $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$។
ឧទាហរណ៍ #3
ស្វែងរក $\lim_(x\to(0))\frac(\sin(9x))(x)$ ។
ចាប់តាំងពី $\lim_(x\to(0))\sin(9x)=0$ និង $\lim_(x\to(0))x=0$ យើងកំពុងដោះស្រាយជាមួយនឹងភាពមិនច្បាស់លាស់នៃទម្រង់ $\frac( 0 )(0)$ ឧ. បានអនុវត្ត។ ទោះយ៉ាងណាក៏ដោយ កន្សោមនៅក្រោមសញ្ញាស៊ីនុស និងក្នុងភាគបែងមិនត្រូវគ្នាទេ។ នៅទីនេះវាត្រូវបានទាមទារដើម្បីកែសម្រួលកន្សោមនៅក្នុងភាគបែងទៅជាទម្រង់ដែលចង់បាន។ យើងត្រូវការកន្សោម $9x$ ដើម្បីស្ថិតនៅក្នុងភាគបែង - បន្ទាប់មកវានឹងក្លាយជាការពិត។ សំខាន់ យើងខ្វះកត្តា $9$ ក្នុងភាគបែង ដែលវាមិនពិបាកបញ្ចូលនោះទេ គ្រាន់តែគុណកន្សោមក្នុងភាគបែងដោយ $9។ តាមធម្មជាតិ ដើម្បីប៉ះប៉ូវគុណនឹង ៩ ដុល្លារ អ្នកនឹងត្រូវចែកភ្លាមៗដោយ ៩ ដុល្លារ ហើយចែក៖
$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x) $$
ឥឡូវនេះកន្សោមនៅក្នុងភាគបែង និងនៅក្រោមសញ្ញាស៊ីនុសគឺដូចគ្នា។ លក្ខខណ្ឌទាំងពីរសម្រាប់ដែនកំណត់ $\lim_(x\to(0))\frac(\sin(9x))(9x)$ ត្រូវបានពេញចិត្ត។ ដូច្នេះ $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$ ។ ហើយនេះមានន័យថា៖
$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$
ចម្លើយ៖ $\lim_(x\to(0))\frac(\sin(9x))(x)=9$ ។
ឧទាហរណ៍ #4
ស្វែងរក $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$ ។
ចាប់តាំងពី $\lim_(x\to(0))\sin(5x)=0$ និង $\lim_(x\to(0))\tg(8x)=0$ នៅទីនេះ យើងកំពុងដោះស្រាយជាមួយនឹងភាពមិនច្បាស់លាស់នៃ ទម្រង់ $\frac(0)(0)$ ។ ទោះជាយ៉ាងណាក៏ដោយទម្រង់នៃដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងត្រូវបានខូច។ ភាគយកដែលមាន $\sin(5x)$ ទាមទារ $5x$ ក្នុងភាគបែង។ ក្នុងស្ថានភាពនេះ វិធីងាយស្រួលបំផុតគឺត្រូវចែកភាគយកដោយ $5x$ ហើយគុណនឹង $5x$ ភ្លាមៗ។ លើសពីនេះទៀត យើងនឹងធ្វើប្រតិបត្តិការស្រដៀងគ្នាជាមួយភាគបែង គុណ និងចែក $\tg(8x)$ ដោយ $8x$:
$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
កាត់បន្ថយ $x$ ហើយយក $\frac(5)(8)$ ថេរចេញពីសញ្ញាកំណត់ យើងទទួលបាន៖
$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x)))( 8x)) $$
ចំណាំថា $\lim_(x\to(0))\frac(\sin(5x))(5x)$ បំពេញបានពេញលេញនូវតម្រូវការសម្រាប់ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។ ដើម្បីស្វែងរក $\lim_(x\to(0))\frac(\tg(8x))(8x)$ រូបមន្តខាងក្រោមគឺអាចអនុវត្តបាន៖
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1)=\frac(5)(8)។ $$
ចម្លើយ៖ $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$។
ឧទាហរណ៍ #5
ស្វែងរក $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$ ។
ចាប់តាំងពី $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (រំលឹកថា $\cos(0)=1$) និង $\ lim_(x\to(0))x^2=0$ បន្ទាប់មកយើងកំពុងដោះស្រាយជាមួយនឹងភាពមិនច្បាស់លាស់នៃទម្រង់ $\frac(0)(0)$។ ទោះយ៉ាងណាក៏ដោយ ដើម្បីអនុវត្តដែនកំណត់ដ៏អស្ចារ្យដំបូង អ្នកគួរតែកម្ចាត់កូស៊ីនុសនៅក្នុងភាគយកដោយចូលទៅកាន់ស៊ីនុស (ដើម្បីអនុវត្តរូបមន្ត) ឬតង់ហ្សង់ (ដើម្បីអនុវត្តរូបមន្ត)។ អ្នកអាចធ្វើវាជាមួយនឹងការបំប្លែងដូចខាងក្រោម៖
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$$$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x))$$
តោះត្រឡប់ទៅដែនកំណត់៖
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$
ប្រភាគ $\frac(\sin^2(5x))(x^2)$ គឺនៅជិតទម្រង់ដែលត្រូវការសម្រាប់ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងរួចទៅហើយ។ ចូរធ្វើការបន្តិចជាមួយនឹងប្រភាគ $\frac(\sin^2(5x))(x^2)$ ដោយកែតម្រូវវាទៅដែនកំណត់ដ៏អស្ចារ្យដំបូង (ចំណាំថាកន្សោមនៅក្នុងភាគយក និងនៅក្រោមស៊ីនុសត្រូវតែផ្គូផ្គង)៖
$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$
ចូរយើងត្រលប់ទៅដែនកំណត់ដែលបានពិចារណា៖
$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0) ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) = 25 ។ $$
ចម្លើយ៖ $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$ ។
ឧទាហរណ៍ #6
ស្វែងរកដែនកំណត់ $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$ ។
ចាប់តាំងពី $\lim_(x\to(0))(1-\cos(6x))=0$ និង $\lim_(x\to(0))(1-\cos(2x))=0$ បន្ទាប់មក យើងកំពុងដោះស្រាយជាមួយនឹងភាពមិនច្បាស់លាស់នៃ $\frac(0)(0)$ ។ តោះបើកវាដោយមានជំនួយពីដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។ ដើម្បីធ្វើដូចនេះសូមផ្លាស់ទីពីកូស៊ីនុសទៅស៊ីនុស។ ចាប់តាំងពី $1-\cos(2\alpha)=2\sin^2(\alpha)$ បន្ទាប់មក៖
$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x)។$$
ឆ្លងកាត់ដែនកំណត់ដែលបានផ្តល់ឱ្យ sines យើងនឹងមាន:
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x)))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))(((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$
ចម្លើយ៖ $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$ ។
ឧទាហរណ៍ #7
គណនាដែនកំណត់ $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ បានផ្តល់ $\alpha\neq\beta $
ការពន្យល់លម្អិតត្រូវបានផ្តល់ឱ្យមុននេះ ប៉ុន្តែនៅទីនេះយើងគ្រាន់តែកត់សំគាល់ថា មានភាពមិនច្បាស់លាស់នៃ $\frac(0)(0)$ ម្តងទៀត។ ចូរផ្លាស់ទីពីកូស៊ីនុសទៅស៊ីនុសដោយប្រើរូបមន្ត
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$
ដោយប្រើរូបមន្តខាងលើយើងទទួលបាន៖
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\ ត្រូវ| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta) )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x) \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alpha^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2)។ $$
ចម្លើយ៖ $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ អាល់ហ្វា^2)(2)$។
ឧទាហរណ៍ #8
ស្វែងរកដែនកំណត់ $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$។
ចាប់តាំងពី $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (រំលឹកថា $\sin(0)=\tg(0)=0$) និង $\ lim_(x\to(0))x^3=0$ បន្ទាប់មកនៅទីនេះ យើងកំពុងដោះស្រាយជាមួយនឹងភាពមិនច្បាស់លាស់នៃទម្រង់ $\frac(0)(0)$។ ចូរបំបែកវាដូចនេះ៖
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3)=\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x)))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) = \\ frac (1) (2) ។ $$
ចម្លើយ៖ $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$។
ឧទាហរណ៍ #9
ស្វែងរកដែនកំណត់ $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$។
ចាប់តាំងពី $\lim_(x\to(3))(1-\cos(x-3))=0$ និង $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$ បន្ទាប់មកមានភាពមិនច្បាស់លាស់នៃទម្រង់ $\frac(0)(0)$។ មុននឹងបន្តការពង្រីករបស់វា វាងាយស្រួលក្នុងការផ្លាស់ប្តូរអថេរតាមរបៀបដែលអថេរថ្មីមានទំនោរទៅសូន្យ (ចំណាំថាអថេរ $\alpha \to 0$ ក្នុងរូបមន្ត)។ មធ្យោបាយងាយស្រួលបំផុតគឺត្រូវណែនាំអថេរ $t=x-3$ ។ ទោះជាយ៉ាងណាក៏ដោយ សម្រាប់ភាពងាយស្រួលនៃការផ្លាស់ប្តូរបន្ថែមទៀត (អត្ថប្រយោជន៍នេះអាចត្រូវបានគេមើលឃើញនៅក្នុងដំណើរការនៃដំណោះស្រាយខាងក្រោម) វាមានតម្លៃធ្វើការជំនួសដូចខាងក្រោម: $t=\frac(x-3)(2)$ ។ ខ្ញុំកត់សម្គាល់ថាការជំនួសទាំងពីរអាចអនុវត្តបានក្នុងករណីនេះ គ្រាន់តែការជំនួសទីពីរនឹងអនុញ្ញាតឱ្យអ្នកធ្វើការតិចជាងដោយប្រភាគ។ ចាប់តាំងពី $x\to(3)$ បន្ទាប់មក $t\to(0)$។
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\ ត្រូវ| =\left|\begin(aligned)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$
ចម្លើយ៖ $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$ ។
ឧទាហរណ៍ #10
ស្វែងរកដែនកំណត់ $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^ 2) $ ។
ជាថ្មីម្តងទៀត យើងកំពុងដោះស្រាយជាមួយនឹងភាពមិនច្បាស់លាស់នៃ $\frac(0)(0)$។ មុនពេលបន្តទៅការពង្រីករបស់វា វាងាយស្រួលក្នុងការផ្លាស់ប្តូរអថេរតាមរបៀបដែលអថេរថ្មីមានទំនោរទៅសូន្យ (ចំណាំថានៅក្នុងរូបមន្តអថេរគឺ $\alpha\to(0)$)។ មធ្យោបាយងាយស្រួលបំផុតគឺត្រូវណែនាំអថេរ $t=\frac(\pi)(2)-x$ ។ ចាប់តាំងពី $x\to\frac(\pi)(2)$ បន្ទាប់មក $t\to(0)$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\left|\frac(0)(0)\right| =\left|\begin(aligned)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0) ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) = \\ frac (1) (2) ។ $$
ចម្លើយ៖ $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$។
ឧទាហរណ៍ #11
ស្វែងរកដែនកំណត់ $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2\ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$ ។
ក្នុងករណីនេះយើងមិនចាំបាច់ប្រើដែនកំណត់ដ៏អស្ចារ្យដំបូងឡើយ។ សូមចំណាំ៖ នៅក្នុងដែនកំណត់ទីមួយ និងទីពីរ មានតែអនុគមន៍ត្រីកោណមាត្រ និងលេខប៉ុណ្ណោះ។ ជាញឹកញាប់នៅក្នុងឧទាហរណ៍នៃប្រភេទនេះ វាគឺអាចធ្វើទៅបានដើម្បីសម្រួលការបញ្ចេញមតិដែលមានទីតាំងនៅក្រោមសញ្ញាកំណត់។ ក្នុងករណីនេះបន្ទាប់ពីការធ្វើឱ្យសាមញ្ញដែលបានរៀបរាប់និងកាត់បន្ថយកត្តាមួយចំនួនភាពមិនច្បាស់លាស់នឹងរលាយបាត់។ ខ្ញុំបានផ្តល់ឧទាហរណ៍នេះក្នុងគោលបំណងតែមួយគត់៖ ដើម្បីបង្ហាញថាវត្តមាននៃអនុគមន៍ត្រីកោណមាត្រនៅក្រោមសញ្ញាកំណត់ មិនចាំបាច់មានន័យថាការអនុវត្តដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងឡើយ។
ចាប់តាំងពី $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (រំលឹកថា $\sin\frac(\pi)(2)=1$) និង $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (រំលឹកថា $\cos\frac(\pi)(2)=0$) បន្ទាប់មក យើងដោះស្រាយជាមួយភាពមិនច្បាស់លាស់ នៃទម្រង់ $\frac(0)(0)$ ។ ទោះជាយ៉ាងណាក៏ដោយនេះមិនមានន័យទាល់តែសោះដែលយើងត្រូវប្រើដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។ ដើម្បីបង្ហាញភាពមិនច្បាស់លាស់ វាគ្រប់គ្រាន់ក្នុងការពិចារណាថា $\cos^2x=1-\sin^2x$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))))=\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x))=\frac(1)(1+1)=\frac(1)(2)។ $$
មានដំណោះស្រាយស្រដៀងគ្នានៅក្នុងសៀវភៅដំណោះស្រាយរបស់ Demidovich (លេខ 475) ។ ចំពោះដែនកំណត់ទីពីរ ដូចនៅក្នុងឧទាហរណ៍មុននៃផ្នែកនេះ យើងមានភាពមិនច្បាស់លាស់នៃទម្រង់ $\frac(0)(0)$។ ហេតុអ្វីបានជាវាកើតឡើង? វាកើតឡើងដោយសារតែ $\tg\frac(2\pi)(3)=-\sqrt(3)$ និង $2\cos\frac(2\pi)(3)=-1$ ។ យើងប្រើតម្លៃទាំងនេះដើម្បីបំប្លែងកន្សោមក្នុងភាគយក និងភាគបែង។ គោលបំណងនៃសកម្មភាពរបស់យើង៖ សរសេរផលបូកក្នុងភាគយក និងភាគបែងជាផលិតផល។ ដោយវិធីនេះ ជារឿយៗវាងាយស្រួលក្នុងការផ្លាស់ប្តូរអថេរក្នុងទម្រង់ស្រដៀងគ្នា ដូច្នេះអថេរថ្មីមានទំនោរទៅសូន្យ (សូមមើលឧទាហរណ៍ឧទាហរណ៍លេខ 9 ឬលេខ 10 នៅលើទំព័រនេះ)។ ទោះយ៉ាងណាក៏ដោយ ក្នុងឧទាហរណ៍នេះ វាគ្មានចំណុចណាមួយក្នុងការជំនួសអថេរនោះទេ ទោះបីជាប្រសិនបើចង់បាន ការជំនួសអថេរ $t=x-\frac(2\pi)(3)$ គឺងាយស្រួលអនុវត្ត។
$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ ទៅ\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x))+\frac(1)(2)\right )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin) \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac) (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3) ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3) ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4 )(\sqrt(3))។ $$
ដូចដែលអ្នកអាចឃើញ យើងមិនចាំបាច់អនុវត្តដែនកំណត់ដ៏អស្ចារ្យដំបូងឡើយ។ ជាការពិតណាស់ នេះអាចត្រូវបានធ្វើប្រសិនបើចង់បាន (សូមមើលកំណត់សម្គាល់ខាងក្រោម) ប៉ុន្តែវាមិនចាំបាច់ទេ។
តើអ្វីនឹងជាដំណោះស្រាយដោយប្រើកម្រិតគួរឱ្យកត់សម្គាល់ដំបូង? បង្ហាញ/លាក់
ដោយប្រើដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងយើងទទួលបាន:
$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3))\ ស្តាំ))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3)))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3)))( 2) \cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3)) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( ៣)). $$
ចម្លើយ៖ $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( ៣))$។
ស្វែងរកដែនកំណត់ដ៏អស្ចារ្យវាពិបាកមិនត្រឹមតែសម្រាប់និស្សិតជាច្រើននៃការសិក្សាឆ្នាំទី 1 និងទី 2 ដែលសិក្សាទ្រឹស្ដីដែនកំណត់ប៉ុណ្ណោះទេ ប៉ុន្តែក៏មានគ្រូបង្រៀនមួយចំនួនផងដែរ។
រូបមន្តនៃដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង
ផលវិបាកនៃដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង
សរសេររូបមន្ត
1. 2. 3. 4. ប៉ុន្តែដោយខ្លួនគេ រូបមន្តទូទៅនៃដែនកំណត់គួរឱ្យកត់សម្គាល់មិនជួយនរណាម្នាក់ក្នុងការប្រឡង ឬតេស្តនោះទេ។ ចំណុចសំខាន់គឺថា ភារកិច្ចពិតប្រាកដត្រូវបានបង្កើតឡើង ដូច្នេះរូបមន្តដែលបានសរសេរខាងលើនៅតែត្រូវការមកដល់។ ហើយសិស្សភាគច្រើនដែលរំលងថ្នាក់ សិក្សាវគ្គសិក្សានេះដោយការឆ្លើយឆ្លង ឬមានគ្រូដែលខ្លួនពួកគេតែងតែមិនយល់ពីអ្វីដែលពួកគេកំពុងពន្យល់ មិនអាចគណនាឧទាហរណ៍បឋមភាគច្រើនដល់កម្រិតគួរឱ្យកត់សម្គាល់នោះទេ។ ពីរូបមន្តនៃដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង យើងឃើញថាពួកវាអាចត្រូវបានប្រើដើម្បីស៊ើបអង្កេតភាពមិនច្បាស់លាស់ដូចជាសូន្យ បែងចែកដោយសូន្យសម្រាប់កន្សោមដែលមានអនុគមន៍ត្រីកោណមាត្រ។ ចូរយើងពិចារណាជាដំបូងនូវឧទាហរណ៍មួយចំនួននៅលើដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង ហើយបន្ទាប់មកយើងនឹងសិក្សាអំពីដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ។
ឧទាហរណ៍ 1. ស្វែងរកដែនកំណត់នៃអនុគមន៍ sin(7*x)/(5*x)
ដំណោះស្រាយ៖ ដូចដែលអ្នកអាចឃើញមុខងារនៅក្រោមដែនកំណត់គឺនៅជិតដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងប៉ុន្តែដែនកំណត់នៃមុខងារខ្លួនវាគឺពិតជាមិនស្មើនឹងមួយ។ នៅក្នុងការចាត់តាំងក្នុងដែនកំណត់បែបនេះ អ្នកគួរតែដាក់ចេញនៅក្នុងភាគបែងនៃអថេរដែលមានមេគុណដូចគ្នាដែលមាននៅក្នុងអថេរនៅក្រោមស៊ីនុស។ ក្នុងករណីនេះចែកនិងគុណនឹង 7 ![]()
សម្រាប់អ្នកខ្លះ ការលម្អិតបែបនេះនឹងហាក់បីដូចជាគ្មានប្រយោជន៍ ប៉ុន្តែសម្រាប់សិស្សភាគច្រើនដែលពិបាកក្នុងការផ្តល់ដែនកំណត់ វានឹងជួយឱ្យយល់កាន់តែច្បាស់អំពីច្បាប់ និងរៀនទ្រឹស្តី។
ដូចគ្នានេះផងដែរប្រសិនបើមានទម្រង់បញ្ច្រាសនៃមុខងារ - នេះក៏ជាដែនកំណត់ដ៏អស្ចារ្យដំបូងគេផងដែរ។ ហើយទាំងអស់ដោយសារតែដែនកំណត់ដ៏អស្ចារ្យគឺស្មើនឹងមួយ។
ច្បាប់ដូចគ្នានេះអនុវត្តចំពោះផលវិបាកនៃ 1 ដែនកំណត់គួរឱ្យកត់សម្គាល់។ ដូច្នេះប្រសិនបើអ្នកត្រូវបានគេសួរថា "តើអ្វីជាដែនកំណត់ដ៏អស្ចារ្យដំបូង?" អ្នកត្រូវតែឆ្លើយដោយមិនស្ទាក់ស្ទើរថាវាជាឯកតា។
ឧទាហរណ៍ 2. ស្វែងរកដែនកំណត់នៃអនុគមន៍ sin(6x)/tan(11x)
ដំណោះស្រាយ៖ ដើម្បីយល់ពីលទ្ធផលចុងក្រោយ យើងសរសេរមុខងារក្នុងទម្រង់ 
ដើម្បីអនុវត្តច្បាប់នៃដែនកំណត់គួរឱ្យកត់សម្គាល់គុណនិងចែកដោយកត្តា
បន្ទាប់យើងសរសេរដែនកំណត់នៃផលិតផលនៃមុខងារនៅក្នុងលក្ខខណ្ឌនៃផលិតផលនៃដែនកំណត់ 
ដោយគ្មានរូបមន្តស្មុគស្មាញ យើងបានរកឃើញដែនកំណត់នៃអនុគមន៍ត្រីកោណមាត្រមួយចំនួន។ ដើម្បីរៀនរូបមន្តសាមញ្ញ សូមព្យាយាមមកជាមួយនិងស្វែងរកដែនកំណត់នៅលើ 2 និង 4 រូបមន្តនៃកូរ៉ូឡារីទី 1 នៃដែនកំណត់ដ៏អស្ចារ្យ។ យើងនឹងពិចារណាការងារស្មុគស្មាញបន្ថែមទៀត។
ឧទាហរណ៍ 3. គណនាដែនកំណត់ (1-cos(x))/x^2
ដំណោះស្រាយ៖ នៅពេលពិនិត្យដោយការជំនួស យើងទទួលបានភាពមិនច្បាស់លាស់ 0/0 ។ មនុស្សជាច្រើនមិនដឹងពីរបៀបកាត់បន្ថយឧទាហរណ៍បែបនេះទៅ 1 ដែនកំណត់ដ៏អស្ចារ្យ។ នៅទីនេះអ្នកគួរប្រើរូបមន្តត្រីកោណមាត្រ ![]()
ក្នុងករណីនេះ ដែនកំណត់នឹងត្រូវបានបំប្លែងទៅជាទម្រង់ច្បាស់លាស់ 
យើងបានទទួលជោគជ័យក្នុងការកាត់បន្ថយមុខងារទៅជាការ៉េនៃដែនកំណត់គួរឱ្យកត់សម្គាល់។
ឧទាហរណ៍ 4. ស្វែងរកដែនកំណត់
ដំណោះស្រាយ៖ នៅពេលជំនួស យើងទទួលបានឯកវចនៈដែលធ្លាប់ស្គាល់ 0/0 ។ ទោះយ៉ាងណាក៏ដោយ អថេរចូលទៅជិត Pi មិនមែនសូន្យទេ។ ដូច្នេះ ដើម្បីអនុវត្តដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង យើងនឹងធ្វើការផ្លាស់ប្តូរបែបនេះនៅក្នុងអថេរ x ដូច្នេះអថេរថ្មីទៅសូន្យ។ ដើម្បីធ្វើដូច្នេះ យើងកំណត់ភាគបែងជាអថេរថ្មី Pi-x=y 
ដូច្នេះដោយប្រើរូបមន្តត្រីកោណមាត្រដែលត្រូវបានផ្តល់ឱ្យក្នុងកិច្ចការមុនឧទាហរណ៍ត្រូវបានកាត់បន្ថយមកត្រឹម 1 ដែនកំណត់គួរឱ្យកត់សម្គាល់។
ឧទាហរណ៍ 5 គណនាដែនកំណត់ ![]() ដំណោះស្រាយ៖ ដំបូងឡើយ វាមិនច្បាស់អំពីរបៀបធ្វើឱ្យកម្រិតកំណត់ងាយស្រួលនោះទេ។ ប៉ុន្តែប្រសិនបើមានឧទាហរណ៍ នោះត្រូវតែមានចម្លើយ។ ការពិតដែលថាអថេរទៅឯកតាផ្តល់ឱ្យ នៅពេលជំនួសឯកវចនៈនៃទម្រង់សូន្យគុណនឹងភាពគ្មានទីបញ្ចប់ ដូច្នេះតង់សង់ត្រូវតែជំនួសដោយរូបមន្ត
ដំណោះស្រាយ៖ ដំបូងឡើយ វាមិនច្បាស់អំពីរបៀបធ្វើឱ្យកម្រិតកំណត់ងាយស្រួលនោះទេ។ ប៉ុន្តែប្រសិនបើមានឧទាហរណ៍ នោះត្រូវតែមានចម្លើយ។ ការពិតដែលថាអថេរទៅឯកតាផ្តល់ឱ្យ នៅពេលជំនួសឯកវចនៈនៃទម្រង់សូន្យគុណនឹងភាពគ្មានទីបញ្ចប់ ដូច្នេះតង់សង់ត្រូវតែជំនួសដោយរូបមន្ត ![]()
បន្ទាប់ពីនោះយើងទទួលបានភាពមិនច្បាស់លាស់ដែលចង់បាន 0/0 ។ បន្ទាប់មក យើងធ្វើការផ្លាស់ប្តូរអថេរក្នុងដែនកំណត់ ហើយប្រើរយៈពេលនៃកូតង់សង់ 
ការជំនួសចុងក្រោយអនុញ្ញាតឱ្យយើងប្រើកូរ៉ូឡារី 1 នៃដែនកំណត់គួរឱ្យកត់សម្គាល់។
ដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរគឺស្មើនឹងនិទស្សន្ត
 នេះជារឿងបុរាណដែលក្នុងបញ្ហាពិតប្រាកដ វាមិនងាយស្រួលក្នុងការឈានដល់កម្រិតកំណត់នោះទេ។
នេះជារឿងបុរាណដែលក្នុងបញ្ហាពិតប្រាកដ វាមិនងាយស្រួលក្នុងការឈានដល់កម្រិតកំណត់នោះទេ។
សម្រាប់ការគណនាអ្នកនឹងត្រូវការ ដែនកំណត់គឺជាផលវិបាកនៃដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ៖
1.  2.
2.  3.
3. ![]() 4.
4.
សូមអរគុណដល់ដែនកំណត់ដ៏គួរឱ្យកត់សម្គាល់ទីពីរ និងផលវិបាករបស់វា មនុស្សម្នាក់អាចស្វែងយល់ពីភាពមិនច្បាស់លាស់ដូចជា សូន្យបែងចែកដោយសូន្យ មួយទៅថាមពលនៃភាពគ្មានទីបញ្ចប់ និងភាពគ្មានទីបញ្ចប់ដែលបែងចែកដោយភាពគ្មានទីបញ្ចប់ និងសូម្បីតែដល់កម្រិតដូចគ្នា។ 
ចូរចាប់ផ្តើមជាមួយនឹងឧទាហរណ៍សាមញ្ញមួយចំនួន។
ឧទាហរណ៍ ៦ ស្វែងរកដែនកំណត់នៃមុខងារ
ដំណោះស្រាយ៖ អនុវត្តដោយផ្ទាល់នូវដែនកំណត់ដ៏អស្ចារ្យចំនួន 2 នឹងមិនដំណើរការទេ។ ដំបូងអ្នកត្រូវបង្វែរសូចនាករដើម្បីឱ្យវាមានទម្រង់បញ្ច្រាសទៅពាក្យក្នុងតង្កៀប 
នេះគឺជាបច្ចេកទេសនៃការកាត់បន្ថយដល់ 2 ដែនកំណត់គួរឱ្យកត់សម្គាល់ហើយតាមការពិតការចេញនៃរូបមន្ត 2 នៃផលវិបាកនៃដែនកំណត់។
ឧទាហរណ៍ ៧ ស្វែងរកដែនកំណត់នៃមុខងារ
ដំណោះស្រាយ: យើងមានភារកិច្ចសម្រាប់រូបមន្ត 3 នៃកូរ៉ូឡារីទី 2 នៃដែនកំណត់គួរឱ្យកត់សម្គាល់។ ការជំនួសសូន្យផ្តល់នូវឯកវចនៈនៃទម្រង់ 0/0 ។ ដើម្បីដំឡើងដែនកំណត់នៅក្រោមច្បាប់ យើងបង្វែរភាគបែងដើម្បីឱ្យអថេរមានមេគុណដូចគ្នានឹងលោការីត ![]()
វាក៏ងាយស្រួលយល់ និងអនុវត្តនៅពេលប្រឡង។ ការលំបាករបស់សិស្សក្នុងការគណនាដែនកំណត់ចាប់ផ្តើមជាមួយនឹងកិច្ចការខាងក្រោម។
ឧទាហរណ៍ ៨ គណនាដែនកំណត់មុខងារ[(x+7)/(x-3)]^(x-2)  ដំណោះស្រាយ៖ យើងមានឯកវចនៈនៃប្រភេទទី ១ ទៅនឹងថាមពលនៃភាពគ្មានទីបញ្ចប់។ ប្រសិនបើអ្នកមិនជឿខ្ញុំ អ្នកអាចជំនួសភាពគ្មានទីបញ្ចប់ជំនួសឱ្យ "x" គ្រប់ទីកន្លែង ហើយមើលដោយខ្លួនឯង។ ដើម្បីលើកក្រោមក្បួន យើងបែងចែកភាគយកដោយភាគបែងក្នុងតង្កៀប សម្រាប់នេះដំបូងយើងអនុវត្តឧបាយកល
ដំណោះស្រាយ៖ យើងមានឯកវចនៈនៃប្រភេទទី ១ ទៅនឹងថាមពលនៃភាពគ្មានទីបញ្ចប់។ ប្រសិនបើអ្នកមិនជឿខ្ញុំ អ្នកអាចជំនួសភាពគ្មានទីបញ្ចប់ជំនួសឱ្យ "x" គ្រប់ទីកន្លែង ហើយមើលដោយខ្លួនឯង។ ដើម្បីលើកក្រោមក្បួន យើងបែងចែកភាគយកដោយភាគបែងក្នុងតង្កៀប សម្រាប់នេះដំបូងយើងអនុវត្តឧបាយកល ![]()
ជំនួសកន្សោមទៅក្នុងដែនកំណត់ ហើយបង្វែរវាទៅដែនកំណត់ដ៏អស្ចារ្យ 2 
ដែនកំណត់គឺជានិទស្សន្តនៃអំណាចនៃ 10 ។ ថេរដែលជាពាក្យដែលមានអថេរទាំងក្នុងតង្កៀប និងសញ្ញាប័ត្រមិនរួមចំណែក "អាកាសធាតុ" ណាមួយទេ - នេះគួរតែត្រូវបានចងចាំ។ ហើយប្រសិនបើគ្រូសួរអ្នក - "ហេតុអ្វីបានជាអ្នកមិនបើកសូចនាករ?" (សម្រាប់ឧទាហរណ៍នេះក្នុង x-3 ) បន្ទាប់មកនិយាយថា "នៅពេលដែលអថេរមានទំនោរទៅរកភាពគ្មានទីបញ្ចប់ បន្ទាប់មកបន្ថែម 100 ទៅវា ឬដក 1000 ហើយដែនកំណត់នឹងនៅដដែល!"។
មានវិធីទីពីរដើម្បីគណនាដែនកំណត់នៃប្រភេទនេះ។ យើងនឹងនិយាយអំពីវានៅក្នុងកិច្ចការបន្ទាប់។
ឧទាហរណ៍ ៩ ស្វែងរកដែនកំណត់  ដំណោះស្រាយ៖ ឥឡូវនេះ យើងដកអថេរនៅក្នុងភាគយក និងភាគបែង ហើយបង្វែរមុខងារមួយទៅជាមុខងារមួយទៀត។ ដើម្បីទទួលបានតម្លៃចុងក្រោយ យើងប្រើរូបមន្តនៃកូរ៉ូឡារី 2 នៃដែនកំណត់គួរឱ្យកត់សម្គាល់
ដំណោះស្រាយ៖ ឥឡូវនេះ យើងដកអថេរនៅក្នុងភាគយក និងភាគបែង ហើយបង្វែរមុខងារមួយទៅជាមុខងារមួយទៀត។ ដើម្បីទទួលបានតម្លៃចុងក្រោយ យើងប្រើរូបមន្តនៃកូរ៉ូឡារី 2 នៃដែនកំណត់គួរឱ្យកត់សម្គាល់ 
ឧទាហរណ៍ 10 ស្វែងរកដែនកំណត់នៃមុខងារ ដំណោះស្រាយ៖ មិនមែនគ្រប់គ្នាអាចរកឃើញដែនកំណត់ដែលបានផ្តល់ឱ្យនោះទេ។ ដើម្បីបង្កើនដែនកំណត់ដល់ 2 សូមស្រមៃថាអំពើបាប (3x) គឺជាអថេរមួយ ហើយអ្នកត្រូវបង្វែរនិទស្សន្ត
ដំណោះស្រាយ៖ មិនមែនគ្រប់គ្នាអាចរកឃើញដែនកំណត់ដែលបានផ្តល់ឱ្យនោះទេ។ ដើម្បីបង្កើនដែនកំណត់ដល់ 2 សូមស្រមៃថាអំពើបាប (3x) គឺជាអថេរមួយ ហើយអ្នកត្រូវបង្វែរនិទស្សន្ត 
បន្ទាប់យើងសរសេរសូចនាករជាសញ្ញាប័ត្រក្នុងមួយដឺក្រេ 
អាគុយម៉ង់កម្រិតមធ្យមត្រូវបានពិពណ៌នានៅក្នុងវង់ក្រចក។ ជាលទ្ធផលនៃការប្រើប្រាស់ដែនកំណត់ដ៏អស្ចារ្យទីមួយ និងទីពីរ យើងទទួលបាននិទស្សន្តគូប។
ឧទាហរណ៍ 11 ។ គណនាដែនកំណត់មុខងារ sin(2*x)/log(3*x+1)
ដំណោះស្រាយ៖ យើងមានភាពមិនច្បាស់លាស់នៃទម្រង់ 0/0។ លើសពីនេះទៀតយើងឃើញថាមុខងារគួរតែត្រូវបានបម្លែងទៅជាការប្រើប្រាស់ដែនកំណត់ដ៏អស្ចារ្យទាំងពីរ។ ចូរយើងអនុវត្តការបំប្លែងគណិតវិទ្យាពីមុន ![]()
លើសពីនេះទៀតដោយគ្មានការលំបាកដែនកំណត់យកតម្លៃ 
នេះជារបៀបដែលអ្នកនឹងមានអារម្មណ៍ស្រួលក្នុងការធ្វើតេស្ត ការធ្វើតេស្ត ម៉ូឌុល ប្រសិនបើអ្នករៀនពីរបៀបលាបពណ៌យ៉ាងឆាប់រហ័ស និងកាត់បន្ថយវាដល់ដែនកំណត់ដ៏អស្ចារ្យទីមួយ ឬទីពីរ។ ប្រសិនបើវាពិបាកសម្រាប់អ្នកក្នុងការទន្ទេញវិធីខាងលើនៃការស្វែងរកដែនកំណត់នោះ អ្នកអាចបញ្ជាការងារត្រួតពិនិត្យលើដែនកំណត់ពីយើងជានិច្ច។
ដើម្បីធ្វើដូច្នេះ បំពេញទម្រង់បែបបទ បញ្ជាក់ទិន្នន័យ និងភ្ជាប់ឯកសារជាមួយឧទាហរណ៍។ យើងបានជួយសិស្សជាច្រើន - យើងអាចជួយអ្នកផងដែរ!
មានដែនកំណត់ដ៏អស្ចារ្យជាច្រើន ប៉ុន្តែអ្វីដែលល្បីបំផុតគឺដែនកំណត់ដ៏អស្ចារ្យទីមួយ និងទីពីរ។ អ្វីដែលគួរឱ្យកត់សម្គាល់អំពីដែនកំណត់ទាំងនេះគឺថាពួកវាត្រូវបានប្រើប្រាស់យ៉ាងទូលំទូលាយ និងអាចប្រើដើម្បីស្វែងរកដែនកំណត់ផ្សេងទៀតដែលជួបប្រទះនៅក្នុងបញ្ហាជាច្រើន។ នេះជាអ្វីដែលយើងនឹងធ្វើនៅក្នុងផ្នែកជាក់ស្តែងនៃមេរៀននេះ។ ដើម្បីដោះស្រាយបញ្ហាដោយកាត់បន្ថយដល់ដែនកំណត់គួរឱ្យកត់សម្គាល់ទីមួយ ឬទីពីរ វាមិនចាំបាច់ក្នុងការបង្ហាញភាពមិនច្បាស់លាស់ដែលមាននៅក្នុងពួកគេទេ ព្រោះតម្លៃនៃដែនកំណត់ទាំងនេះត្រូវបានគណនាដោយអ្នកគណិតវិទូដ៏អស្ចារ្យជាយូរមកហើយ។
ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងហៅថាដែនកំណត់នៃសមាមាត្រនៃស៊ីនុសនៃធ្នូតូចគ្មានកំណត់ទៅនឹងធ្នូដូចគ្នា ដែលបង្ហាញជារង្វាស់រ៉ាដ្យង់៖
ចូរបន្តទៅការដោះស្រាយបញ្ហានៅលើដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។ ចំណាំ៖ ប្រសិនបើអនុគមន៍ត្រីកោណមាត្រស្ថិតនៅក្រោមសញ្ញាកំណត់ នេះស្ទើរតែជាសញ្ញាប្រាកដដែលថាកន្សោមនេះអាចត្រូវបានកាត់បន្ថយដល់ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។
ឧទាហរណ៍ ១ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ ជំនួសវិញ។ xសូន្យនាំទៅរកភាពមិនច្បាស់លាស់៖
![]() .
.
ភាគបែងគឺជាស៊ីនុស ដូច្នេះកន្សោមអាចត្រូវបានកាត់បន្ថយដល់កម្រិតគួរឱ្យកត់សម្គាល់ដំបូង។ តោះចាប់ផ្តើមការផ្លាស់ប្តូរ៖
![]() .
.
នៅក្នុងភាគបែង - ស៊ីនុសនៃ x បីហើយនៅក្នុងភាគយកមាន x តែមួយគត់ដែលមានន័យថាអ្នកត្រូវទទួលបានបី x នៅក្នុងភាគយក។ ដើម្បីអ្វី? ធ្វើបទបង្ហាញ ៣ x = កនិងទទួលបានការបញ្ចេញមតិ។
ហើយយើងមកដល់ការបំរែបំរួលនៃកម្រិតដ៏គួរឲ្យកត់សម្គាល់ដំបូងគេ៖
ព្រោះវាមិនមានបញ្ហាអ្វីដែលអក្សរ (អថេរ) នៅក្នុងរូបមន្តនេះគឺជំនួសឱ្យ X ។
យើងគុណនឹង x ដោយបី ហើយចែកភ្លាមៗ៖
 .
.
ដោយអនុលោមតាមដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងដែលបានកត់សម្គាល់ យើងជំនួសកន្សោមប្រភាគ៖
ឥឡូវនេះយើងអាចដោះស្រាយដែនកំណត់នេះ៖
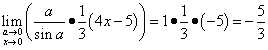 .
.
ឧទាហរណ៍ ២ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ ការជំនួសដោយផ្ទាល់ម្តងទៀតនាំទៅរកភាពមិនច្បាស់លាស់ "សូន្យបែងចែកដោយសូន្យ"៖
![]() .
.
ដើម្បីទទួលបានដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង វាចាំបាច់ដែល x នៅក្រោមសញ្ញាស៊ីនុសនៅក្នុងភាគយក ហើយគ្រាន់តែ x ក្នុងភាគបែងត្រូវមានមេគុណដូចគ្នា។ សូមឲ្យមេគុណនេះស្មើនឹង 2។ ដើម្បីធ្វើដូច្នេះ សូមស្រមៃមើលមេគុណបច្ចុប្បន្ននៅ x ដូចខាងក្រោម ដោយអនុវត្តសកម្មភាពជាមួយប្រភាគ យើងទទួលបាន៖
 .
.
ឧទាហរណ៍ ៣ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ នៅពេលជំនួស យើងទទួលបានភាពមិនច្បាស់លាស់ម្តងទៀត "សូន្យចែកនឹងសូន្យ"៖
 .
.
អ្នកប្រហែលជាយល់រួចហើយថាពីកន្សោមដើមអ្នកអាចទទួលបានដែនកំណត់ដ៏អស្ចារ្យដំបូងគុណនឹងដែនកំណត់ដ៏អស្ចារ្យដំបូង។ ដើម្បីធ្វើដូចនេះយើងបំបែកការេនៃ x ក្នុងភាគយក និងស៊ីនុសក្នុងភាគបែងទៅជាកត្តាដូចគ្នា ហើយដើម្បីទទួលបានមេគុណដូចគ្នាសម្រាប់ x និងស៊ីនុស យើងបែងចែក x ក្នុងភាគយកដោយ 3 និង គុណនឹង 3 ភ្លាមៗ យើងទទួលបាន៖
 .
.
ឧទាហរណ៍ 4ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ ជាថ្មីម្តងទៀតយើងទទួលបានភាពមិនច្បាស់លាស់ "សូន្យបែងចែកដោយសូន្យ"៖
![]() .
.
យើងអាចទទួលបានសមាមាត្រនៃដែនកំណត់គួរឱ្យកត់សម្គាល់ពីរដំបូង។ យើងបែងចែកទាំងភាគយក និងភាគបែងដោយ x ។ បន្ទាប់មក ដើម្បីឱ្យមេគុណនៅស៊ីនុស និង x ស្របគ្នា យើងគុណនឹង x ខាងលើដោយ 2 ហើយចែកភ្លាមៗដោយ 2 ហើយគុណនឹង x ទាបដោយ 3 ហើយចែកនឹង 3 ភ្លាមៗ។

ឧទាហរណ៍ ៥ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ ហើយម្តងទៀតភាពមិនច្បាស់លាស់នៃ "សូន្យបែងចែកដោយសូន្យ":
យើងចងចាំពីត្រីកោណមាត្រថាតង់សង់គឺជាសមាមាត្រនៃស៊ីនុសទៅកូស៊ីនុស ហើយកូស៊ីនុសនៃសូន្យគឺស្មើនឹងមួយ។ យើងធ្វើការផ្លាស់ប្តូរ និងទទួលបាន៖
 .
.
ឧទាហរណ៍ ៦ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ អនុគមន៍ត្រីកោណមាត្រនៅក្រោមសញ្ញាកំណត់ម្តងទៀតបង្ហាញពីគំនិតនៃការអនុវត្តដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។ យើងតំណាងឱ្យវាជាសមាមាត្រនៃស៊ីនុសទៅកូស៊ីនុស។
អត្ថបទនេះ៖ "ដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ" ត្រូវបានឧទ្ទិសដល់ការបង្ហាញនៅក្នុងភាពមិនច្បាស់លាស់នៃប្រភេទសត្វ៖
$ \bigg[\frac(\infty)(\infty)\bigg]^\infty $ និង $^\infty $ ។
ដូចគ្នានេះផងដែរ ភាពមិនច្បាស់លាស់បែបនេះអាចត្រូវបានបង្ហាញដោយប្រើលោការីតនៃអនុគមន៍អិចស្ប៉ូណង់ស្យែល-ថាមពល ប៉ុន្តែនេះគឺជាវិធីសាស្រ្តដំណោះស្រាយមួយផ្សេងទៀត ដែលនឹងត្រូវបានគ្របដណ្តប់នៅក្នុងអត្ថបទមួយផ្សេងទៀត។
រូបមន្តនិងផលវិបាក
រូបមន្តដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរត្រូវបានសរសេរដូចខាងក្រោម: $$ \lim_(x \to \infty) \bigg (1+\frac(1)(x)\bigg)^x = e, \text( where ) e \approx 2.718 $ $
ពីរូបមន្តធ្វើតាម ផលវិបាកដែលងាយស្រួលសម្រាប់ដោះស្រាយឧទាហរណ៍ជាមួយដែនកំណត់៖ $$ \lim_(x \to \infty) \bigg (1 + \frac(k)(x) \bigg)^x = e^k, \text( where ) k \in \mathbb(R) $$ $$$ \lim_(x \to \infty) \bigg (1 + \frac(1)(f(x)) \bigg)^(f(x)) = e$ $$$ \lim_(x \to 0) \bigg (1 + x \bigg)^\frac(1)(x) = e $$
វាគួរតែត្រូវបានកត់សម្គាល់ថាដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរមិនតែងតែត្រូវបានអនុវត្តចំពោះអនុគមន៍អិចស្ប៉ូណង់ស្យែល - ថាមពលនោះទេប៉ុន្តែមានតែនៅក្នុងករណីដែលមូលដ្ឋានមានទំនោរទៅរកការរួបរួមប៉ុណ្ណោះ។ ដើម្បីធ្វើដូចនេះដំបូងត្រូវគណនាដែនកំណត់នៃមូលដ្ឋាននៅក្នុងចិត្តហើយបន្ទាប់មកធ្វើការសន្និដ្ឋាន។ ទាំងអស់នេះនឹងត្រូវបានពិភាក្សានៅក្នុងដំណោះស្រាយឧទាហរណ៍។
ឧទាហរណ៍នៃដំណោះស្រាយ
ពិចារណាឧទាហរណ៍នៃដំណោះស្រាយដោយប្រើរូបមន្តផ្ទាល់និងផលវិបាករបស់វា។ យើងក៏នឹងវិភាគករណីដែលរូបមន្តមិនត្រូវការ។ វាគ្រប់គ្រាន់ហើយក្នុងការសរសេរតែចម្លើយដែលត្រៀមរួចជាស្រេច។
| ឧទាហរណ៍ ១ |
| ស្វែងរកដែនកំណត់ $ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) $ |
| ដំណោះស្រាយ |
|
ការជំនួសភាពគ្មានទីបញ្ចប់ទៅក្នុងដែនកំណត់ ហើយសម្លឹងមើលភាពមិនច្បាស់លាស់៖ $$ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) = \bigg( \frac (\infty)(\infty)\bigg)^\infty $$ ស្វែងរកដែនកំណត់នៃមូលដ្ឋាន៖ $$ \lim_(x\to\infty) \frac(x+4)(x+3)= \lim_(x\to\infty) \frac(x(1+\frac( 4)(x)))(x(1+\frac(3)(x)))) = 1$$ យើងទទួលបានមូលដ្ឋានស្មើនឹងមួយ ដែលមានន័យថាអ្នកអាចអនុវត្តដែនកំណត់ដ៏អស្ចារ្យទីពីររួចហើយ។ ដើម្បីធ្វើដូចនេះ យើងនឹងធ្វើឱ្យសមនឹងមូលដ្ឋាននៃអនុគមន៍ទៅនឹងរូបមន្តដោយដកនិងបន្ថែមមួយ៖ $$ \lim_(x\to\infty) \bigg(1 + \frac(x+4)(x+3) - 1 \bigg)^(x+3) = \lim_(x\to\infty) \ bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = $$ យើងពិនិត្យមើលលទ្ធផលទីពីរ ហើយសរសេរចម្លើយ៖ $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$ ប្រសិនបើអ្នកមិនអាចដោះស្រាយបញ្ហារបស់អ្នកបានទេ សូមផ្ញើវាមកពួកយើង។ យើងនឹងផ្តល់ដំណោះស្រាយលម្អិត។ អ្នកនឹងអាចស្គាល់ខ្លួនឯងជាមួយនឹងវឌ្ឍនភាពនៃការគណនា និងប្រមូលព័ត៌មាន។ នេះនឹងជួយឱ្យអ្នកទទួលបានក្រេឌីតពីគ្រូក្នុងលក្ខណៈទាន់ពេលវេលា! |
| ចម្លើយ |
| $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$ |
| ឧទាហរណ៍ 4 |
| ដោះស្រាយដែនកំណត់ $ \lim_(x\to \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) $ |
| ដំណោះស្រាយ |
|
យើងរកឃើញដែនកំណត់នៃមូលដ្ឋាន ហើយឃើញថា $ \lim_(x\to\infty) \frac(3x^2+4)(3x^2-2) = 1$ ដូច្នេះយើងអាចអនុវត្តដែនកំណត់ដ៏អស្ចារ្យទីពីរ។ តាមស្ដង់ដារ យោងតាមផែនការ យើងបូក និងដកមួយចេញពីមូលដ្ឋាននៃសញ្ញាបត្រ៖ $$ \lim_(x\to \infty) \bigg (1+\frac(3x^2+4)(3x^2-2)-1\bigg) ^(3x) = \lim_(x\to \infty ) \bigg (1+\frac(6)(3x^2-2) \bigg) ^(3x) = $$ យើងកែសម្រួលប្រភាគក្រោមរូបមន្តនៃចំណាំទី 2 ។ ដែនកំណត់៖ $$ = \lim_(x\to \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(3x) = $$ ឥឡូវនេះលៃតម្រូវកម្រិត។ និទស្សន្តត្រូវតែមានប្រភាគស្មើនឹងភាគបែងនៃមូលដ្ឋាន $ \frac(3x^2-2)(6) $ ។ ដើម្បីធ្វើដូចនេះគុណនិងបែងចែកដឺក្រេដោយវាហើយបន្តដោះស្រាយ: $$ = \lim_(x\to \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(\frac(3x^2-2)) (6) \cdot \frac(6)(3x^2-2)\cdot 3x) = \lim_(x\to \infty) e^(\frac(18x)(3x^2-2)) = $$ ដែនកំណត់ដែលស្ថិតនៅក្នុងថាមពលនៅ $e $ គឺ៖ $ \lim_(x\to \infty) \frac(18x)(3x^2-2) = 0$ ។ ដូច្នេះហើយ បន្តដំណោះស្រាយ យើងមាន៖ |
| ចម្លើយ |
| $$ \lim_(x\to \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) = 1$$ |
អនុញ្ញាតឱ្យយើងវិភាគករណីនៅពេលដែលបញ្ហាគឺស្រដៀងគ្នាទៅនឹងដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរប៉ុន្តែត្រូវបានដោះស្រាយដោយគ្មានវា។
នៅក្នុងអត្ថបទ៖ "ដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ៖ ឧទាហរណ៍នៃដំណោះស្រាយ" រូបមន្តត្រូវបានវិភាគ ផលវិបាករបស់វា និងប្រភេទបញ្ហាញឹកញាប់លើប្រធានបទនេះត្រូវបានផ្តល់ឱ្យ។
