Cari nilai eigen dan vektor eigen bagi contoh matriks. Persamaan ciri matriks

SISTEM PERSAMAAN LINEAR HOMOGENEUS

Sistem persamaan linear homogen ialah sistem bentuk

Adalah jelas bahawa dalam kes ini , kerana semua elemen salah satu lajur dalam penentu ini adalah sama dengan sifar.

Oleh kerana yang tidak diketahui ditemui oleh formula , maka dalam kes apabila Δ ≠ 0, sistem mempunyai penyelesaian sifar yang unik x = y = z= 0. Walau bagaimanapun, dalam banyak masalah persoalan sama ada sistem homogen mempunyai penyelesaian selain sifar adalah menarik.

Teorem. Untuk sistem persamaan homogen linear mempunyai penyelesaian bukan sifar, adalah perlu dan mencukupi bahawa Δ ≠ 0.

Jadi, jika penentu ialah Δ ≠ 0, maka sistem mempunyai penyelesaian yang unik. Jika Δ ≠ 0, maka sistem persamaan homogen linear mempunyai bilangan penyelesaian yang tidak terhingga.

Contoh.

Eigenvectors dan Matriks Eigenvalues

Biarkan matriks segi empat sama diberikan , X ialah beberapa lajur matriks yang ketinggiannya bertepatan dengan susunan matriks A. .

Dalam banyak masalah, seseorang perlu mempertimbangkan persamaan untuk X

di mana λ ialah beberapa nombor. Jelas bahawa untuk mana-mana λ persamaan ini mempunyai penyelesaian sifar.

Nombor λ yang persamaan ini mempunyai penyelesaian bukan sifar dipanggil nilai eigen matriks A, tetapi X kerana λ sedemikian dipanggil vektor sendiri matriks A.

Mari kita cari vektor eigen bagi matriks A. Sejauh mana E∙X=X, maka persamaan matriks boleh ditulis semula sebagai atau . Dalam bentuk diperluas, persamaan ini boleh ditulis semula sebagai sistem persamaan linear. sungguh .

Dan oleh itu

Jadi, kami mendapat sistem persamaan linear homogen untuk menentukan koordinat x 1, x2, x 3 vektor X. Untuk sistem mempunyai penyelesaian bukan sifar, adalah perlu dan mencukupi bahawa penentu sistem adalah sama dengan sifar, i.e.

Ini ialah persamaan darjah ke-3 berkenaan dengan λ. Ia dipanggil persamaan ciri matriks A dan berfungsi untuk menentukan nilai eigen λ.

Setiap nilai eigen λ sepadan dengan vektor eigen X, yang koordinatnya ditentukan daripada sistem pada nilai λ yang sepadan.

Contoh.

ALGEBRA VEKTOR. KONSEP VEKTOR

Apabila mengkaji pelbagai cabang fizik, terdapat kuantiti yang ditentukan sepenuhnya dengan menetapkan nilai berangkanya, contohnya, panjang, luas, jisim, suhu, dll. Nilai sedemikian dipanggil skalar. Walau bagaimanapun, sebagai tambahan kepada mereka, terdapat juga kuantiti, untuk penentuan yang, sebagai tambahan kepada nilai berangka, ia juga perlu untuk mengetahui arah mereka di angkasa, sebagai contoh, daya yang bertindak pada badan, kelajuan dan pecutan. badan apabila ia bergerak di angkasa, kekuatan medan magnet pada titik tertentu dalam ruang dan lain-lain. Kuantiti sedemikian dipanggil kuantiti vektor.

Mari kita perkenalkan definisi yang ketat.

Segmen arah Mari kita panggil segmen, berbanding dengan hujung yang diketahui mana antara mereka yang pertama dan yang kedua.

vektor segmen terarah dipanggil, mempunyai panjang tertentu, i.e. Ini adalah segmen dengan panjang tertentu, di mana salah satu titik yang mengehadkannya diambil sebagai permulaan, dan yang kedua - sebagai penghujung. Jika A ialah permulaan vektor, B adalah penghujungnya, maka vektor dilambangkan dengan simbol, di samping itu, vektor sering dilambangkan dengan satu huruf . Dalam rajah, vektor ditunjukkan oleh segmen, dan arahnya dengan anak panah.

modul atau panjang vektor dipanggil panjang segmen terarah yang mentakrifkannya. Ditandakan dengan || atau ||.

Vektor sifar yang dipanggil, yang permulaan dan penghujungnya bertepatan, juga akan dirujuk sebagai vektor. Ia ditanda. Vektor sifar tidak mempunyai arah yang pasti dan modulusnya adalah sama dengan sifar ||=0.

Vektor dan dipanggil kolinear jika ia terletak pada garisan yang sama atau pada garisan selari. Dalam kes ini, jika vektor dan diarahkan sama, kami akan menulis , secara bertentangan.

Vektor yang terletak pada garis lurus selari dengan satah yang sama dipanggil coplanar.

Dua vektor dan dipanggil sama rata jika ia adalah kolinear, mempunyai arah yang sama, dan sama panjang. Dalam kes ini, tulis .

Ia berikutan daripada takrifan kesamaan vektor bahawa vektor boleh digerakkan selari dengan dirinya sendiri dengan meletakkan asalnya pada mana-mana titik dalam ruang.

Sebagai contoh.

OPERASI LINEAR PADA VEKTOR

Mendarab vektor dengan nombor.
Hasil darab vektor dengan nombor λ ialah vektor baharu seperti berikut:

Hasil darab vektor dan nombor λ dilambangkan dengan .

Sebagai contoh, ialah vektor yang menunjuk ke arah yang sama dengan vektor dan mempunyai panjang separuh daripada vektor .

Operasi yang dimasukkan mempunyai yang berikut harta benda:
Penambahan vektor.
Biarkan dan menjadi dua vektor sewenang-wenangnya. Ambil titik sewenang-wenangnya O dan membina vektor. Selepas itu, dari sudut A ketepikan vektor . Vektor yang menghubungkan permulaan vektor pertama dengan penghujung vektor kedua dipanggil jumlah daripada vektor ini dan dilambangkan .

Takrifan yang dirumuskan bagi penambahan vektor dipanggil peraturan segi empat selari, kerana jumlah vektor yang sama boleh diperoleh seperti berikut. Ketepikan daripada perkara itu O vektor dan . Bina segi empat selari pada vektor ini OABC. Oleh kerana vektor , maka vektor , yang merupakan pepenjuru segi empat selari yang dilukis daripada bucu O, jelas akan menjadi jumlah vektor .

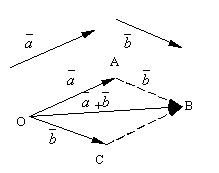
Ia adalah mudah untuk menyemak perkara berikut sifat penambahan vektor.
Perbezaan vektor.
Kolinear vektor kepada vektor tertentu , sama panjang dan berarah bertentangan, dipanggil bertentangan vektor untuk vektor dan dilambangkan dengan . Vektor bertentangan boleh dianggap sebagai hasil pendaraban vektor dengan nombor λ = –1: .

Bagaimana untuk memasukkan formula matematik di tapak?

Jika anda perlu menambah satu atau dua formula matematik pada halaman web, maka cara paling mudah untuk melakukan ini adalah seperti yang diterangkan dalam artikel: formula matematik mudah dimasukkan ke dalam tapak dalam bentuk gambar yang Wolfram Alpha jana secara automatik. Selain kesederhanaan, kaedah universal ini akan membantu meningkatkan keterlihatan tapak dalam enjin carian. Ia telah berfungsi untuk masa yang lama (dan saya fikir ia akan berfungsi selama-lamanya), tetapi ia sudah ketinggalan zaman.

Jika, sebaliknya, anda sentiasa menggunakan formula matematik di tapak anda, maka saya syorkan anda menggunakan MathJax, perpustakaan JavaScript khas yang memaparkan tatatanda matematik dalam pelayar web menggunakan markup MathML, LaTeX atau ASCIIMathML.

Terdapat dua cara untuk mula menggunakan MathJax: (1) menggunakan kod ringkas, anda boleh menyambungkan skrip MathJax ke tapak anda dengan cepat, yang akan dimuatkan secara automatik dari pelayan jauh pada masa yang betul (senarai pelayan); (2) muat naik skrip MathJax dari pelayan jauh ke pelayan anda dan sambungkannya ke semua halaman tapak anda. Kaedah kedua adalah lebih rumit dan memakan masa dan akan membolehkan anda mempercepatkan pemuatan halaman tapak anda, dan jika pelayan MathJax induk menjadi tidak tersedia buat sementara waktu atas sebab tertentu, ini tidak akan menjejaskan tapak anda sendiri dalam apa jua cara. Walaupun kelebihan ini, saya memilih kaedah pertama, kerana ia lebih mudah, lebih cepat dan tidak memerlukan kemahiran teknikal. Ikuti contoh saya, dan dalam masa 5 minit anda akan dapat menggunakan semua ciri MathJax di tapak web anda.

Anda boleh menyambungkan skrip perpustakaan MathJax dari pelayan jauh menggunakan dua pilihan kod yang diambil dari tapak web MathJax utama atau dari halaman dokumentasi:

Salah satu daripada pilihan kod ini perlu disalin dan ditampal ke dalam kod halaman web anda, sebaik-baiknya antara teg Dan atau betul-betul selepas tag . Mengikut pilihan pertama, MathJax memuat lebih cepat dan melambatkan halaman kurang. Tetapi pilihan kedua secara automatik menjejaki dan memuatkan versi terkini MathJax. Jika anda memasukkan kod pertama, maka ia perlu dikemas kini secara berkala. Jika anda menampal kod kedua, maka halaman akan dimuatkan dengan lebih perlahan, tetapi anda tidak perlu sentiasa memantau kemas kini MathJax.

Cara paling mudah untuk menyambungkan MathJax ialah dalam Blogger atau WordPress: dalam panel kawalan tapak, tambahkan widget yang direka untuk memasukkan kod JavaScript pihak ketiga, salin versi pertama atau kedua kod beban yang dibentangkan di atas ke dalamnya dan letakkan widget lebih dekat ke permulaan templat (by the way, ini sama sekali tidak perlu , kerana skrip MathJax dimuatkan secara tak segerak). Itu sahaja. Sekarang pelajari sintaks markup MathML, LaTeX dan ASCIIMathML dan anda sudah bersedia untuk membenamkan formula matematik ke dalam halaman web anda.

Mana-mana fraktal dibina mengikut peraturan tertentu, yang digunakan secara konsisten dalam bilangan kali yang tidak terhad. Setiap masa itu dipanggil lelaran.

Algoritma lelaran untuk membina span Menger agak mudah: kubus asal dengan sisi 1 dibahagikan dengan satah selari dengan mukanya kepada 27 kubus yang sama. Satu kiub pusat dan 6 kiub bersebelahan dengannya di sepanjang muka dikeluarkan daripadanya. Ternyata satu set yang terdiri daripada 20 baki kiub yang lebih kecil. Melakukan perkara yang sama dengan setiap kiub ini, kami mendapat satu set yang terdiri daripada 400 kiub yang lebih kecil. Meneruskan proses ini selama-lamanya, kami mendapat span Menger.

Vektor eigen bagi matriks segi empat sama ialah, apabila didarab dengan matriks tertentu, menghasilkan vektor kolinear. Dengan kata mudah, apabila matriks didarab dengan vektor eigen, yang terakhir tetap sama, tetapi didarab dengan beberapa nombor.

Definisi

Vektor eigen ialah vektor bukan sifar V, yang, apabila didarab dengan matriks persegi M, menjadi dirinya sendiri, ditambah dengan beberapa nombor λ. Dalam tatatanda algebra, ini kelihatan seperti:

M × V = λ × V,

di mana λ ialah nilai eigen bagi matriks M.

Mari kita pertimbangkan contoh berangka. Untuk kemudahan menulis, nombor dalam matriks akan dipisahkan dengan koma bertitik. Katakan kita mempunyai matriks:

M = 0; 4;
6; 10.

Mari kita darabkannya dengan vektor lajur:

V = -2;

Apabila mendarab matriks dengan vektor lajur, kami juga mendapat vektor lajur. Dalam bahasa matematik yang ketat, formula untuk mendarab matriks 2 × 2 dengan vektor lajur akan kelihatan seperti ini:

M × V = M11 × V11 + M12 × V21;
M21 x V11 + M22 x V21.

M11 bermaksud elemen matriks M, berdiri di baris pertama dan lajur pertama, dan M22 ialah elemen yang terletak di baris kedua dan lajur kedua. Untuk matriks kami, unsur-unsur ini ialah M11 = 0, M12 = 4, M21 = 6, M22 10. Untuk vektor lajur, nilai-nilai ini ialah V11 = –2, V21 = 1. Menurut formula ini, kami mendapat yang berikut hasil darab matriks segi empat sama dengan vektor:

M × V = 0 × (-2) + (4) × (1) = 4;
6 × (-2) + 10 × (1) = -2.

Untuk kemudahan, kami menulis vektor lajur ke dalam satu baris. Jadi, kita telah mendarabkan matriks segi empat sama dengan vektor (-2; 1), menghasilkan vektor (4; -2). Jelas sekali, ini adalah vektor yang sama didarab dengan λ = -2. Lambda dalam kes ini menandakan nilai eigen bagi matriks.

Vektor eigen bagi matriks ialah vektor kolinear, iaitu objek yang tidak mengubah kedudukannya dalam ruang apabila ia didarab dengan matriks. Konsep kolineariti dalam algebra vektor adalah serupa dengan istilah keselarian dalam geometri. Dalam tafsiran geometri, vektor kolinear ialah segmen terarah selari dengan panjang yang berbeza. Sejak zaman Euclid, kita tahu bahawa satu baris mempunyai bilangan garis tak terhingga yang selari dengannya, jadi adalah logik untuk mengandaikan bahawa setiap matriks mempunyai bilangan vektor eigen yang tidak terhingga.

Daripada contoh sebelumnya, dapat dilihat bahawa kedua-dua (-8; 4), dan (16; -8), dan (32, -16) boleh menjadi vektor eigen. Semua ini adalah vektor kolinear sepadan dengan nilai eigen λ = -2. Apabila mendarab matriks asal dengan vektor ini, kita masih akan mendapat vektor sebagai hasilnya, yang berbeza daripada asal sebanyak 2 kali. Itulah sebabnya, apabila menyelesaikan masalah untuk mencari vektor eigen, ia diperlukan untuk mencari hanya objek vektor bebas linear. Selalunya, untuk matriks n × n, terdapat nombor n-th bagi vektor eigen. Kalkulator kami direka bentuk untuk analisis matriks segi empat sama tertib kedua, jadi hampir selalu dua vektor eigen akan ditemui sebagai hasilnya, kecuali apabila ia bertepatan.

Dalam contoh di atas, kami mengetahui terlebih dahulu vektor eigen bagi matriks asal dan menentukan nombor lambda secara visual. Walau bagaimanapun, dalam amalan, segala-galanya berlaku sebaliknya: pada mulanya terdapat nilai eigen dan hanya kemudian vektor eigen.

Algoritma penyelesaian

Mari kita lihat semula matriks asal M dan cuba cari kedua-dua vektor eigennya. Jadi matriks kelihatan seperti:

M = 0; 4;
6; 10.

Sebagai permulaan, kita perlu menentukan nilai eigen λ, yang mana kita perlu mengira penentu matriks berikut:

(0 − λ); 4;
6; (10 − λ).

Matriks ini diperoleh dengan menolak λ yang tidak diketahui daripada unsur-unsur pada pepenjuru utama. Penentu ditentukan oleh formula standard:

detA = M11 × M21 − M12 × M22
detA = (0 − λ) × (10 − λ) − 24

Oleh kerana vektor kami tidak boleh sifar, kami mengambil persamaan yang terhasil sebagai bersandar secara linear dan menyamakan detA penentu kami kepada sifar.

(0 − λ) × (10 − λ) − 24 = 0

Mari buka kurungan dan dapatkan persamaan ciri matriks:

λ 2 − 10λ − 24 = 0

Ini adalah persamaan kuadratik piawai yang perlu diselesaikan dari segi diskriminasi.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Punca diskriminasi ialah sqrt(D) = 14, jadi λ1 = -2, λ2 = 12. Sekarang untuk setiap nilai lambda, kita perlu mencari vektor eigen. Mari kita nyatakan pekali sistem untuk λ = -2.

M − λ × E = 2; 4;
6; 12.

Dalam formula ini, E ialah matriks identiti. Berdasarkan matriks yang diperoleh, kami menyusun sistem persamaan linear:

2x + 4y = 6x + 12y

di mana x dan y ialah unsur vektor eigen.

Mari kumpulkan semua X di sebelah kiri dan semua Y di sebelah kanan. Jelas sekali - 4x = 8y. Bahagikan ungkapan dengan - 4 dan dapatkan x = -2y. Sekarang kita boleh menentukan vektor eigen pertama matriks dengan mengambil sebarang nilai yang tidak diketahui (ingat tentang ketakterhinggaan vektor eigen bersandar secara linear). Mari kita ambil y = 1, kemudian x = -2. Oleh itu, vektor eigen pertama kelihatan seperti V1 = (–2; 1). Kembali ke permulaan artikel. Objek vektor inilah yang kita darabkan dengan matriks untuk menunjukkan konsep vektor eigen.

Sekarang mari kita cari vektor eigen untuk λ = 12.

M - λ × E = -12; 4
6; -2.

Mari kita susun sistem persamaan linear yang sama;

-12x + 4y = 6x − 2y
-18x = -6y
3x=y.

Sekarang mari kita ambil x = 1, maka y = 3. Oleh itu, vektor eigen kedua kelihatan seperti V2 = (1; 3). Apabila mendarab matriks asal dengan vektor ini, hasilnya akan sentiasa menjadi vektor yang sama didarab dengan 12. Ini melengkapkan algoritma penyelesaian. Sekarang anda tahu bagaimana untuk menentukan vektor eigen bagi matriks secara manual.

penentu;
surih, iaitu jumlah unsur pada pepenjuru utama;
pangkat, iaitu bilangan maksimum baris/lajur bebas linear.

Program ini beroperasi mengikut algoritma di atas, meminimumkan proses penyelesaian. Adalah penting untuk menunjukkan bahawa dalam program lambda dilambangkan dengan huruf "c". Mari kita lihat contoh berangka.

Contoh program

Mari cuba tentukan vektor eigen untuk matriks berikut:

M=5; 13;
4; 14.

Mari masukkan nilai ini ke dalam sel kalkulator dan dapatkan jawapan dalam bentuk berikut:

Kedudukan matriks: 2;
Penentu matriks: 18;
Surih matriks: 19;
Pengiraan vektor eigen: c 2 − 19.00c + 18.00 (persamaan ciri);
Pengiraan vektor eigen: 18 (nilai lambda pertama);
Pengiraan vektor eigen: 1 (nilai lambda kedua);
Sistem persamaan vektor 1: -13x1 + 13y1 = 4x1 − 4y1;
Sistem persamaan vektor 2: 4x1 + 13y1 = 4x1 + 13y1;
Eigenvector 1: (1; 1);
Eigenvector 2: (-3.25; 1).

Oleh itu, kami telah memperoleh dua vektor eigen bebas linear.

Kesimpulan

Algebra linear dan geometri analitik adalah mata pelajaran standard untuk mana-mana pelajar baru dalam kejuruteraan. Sebilangan besar vektor dan matriks adalah menakutkan, dan mudah untuk membuat kesilapan dalam pengiraan yang menyusahkan itu. Program kami akan membolehkan pelajar menyemak pengiraan mereka atau menyelesaikan masalah mencari vektor eigen secara automatik. Terdapat kalkulator algebra linear lain dalam katalog kami, gunakannya dalam kajian atau kerja anda.

Dengan matriks A, jika terdapat nombor l sehingga AX = lX.

Dalam kes ini, nombor l dipanggil nilai eigen operator (matriks A) sepadan dengan vektor X.

Dalam erti kata lain, vektor eigen ialah vektor yang, di bawah tindakan pengendali linear, berubah menjadi vektor kolinear, i.e. hanya darab dengan beberapa nombor. Sebaliknya, vektor yang tidak betul adalah lebih sukar untuk diubah.

Kami menulis definisi vektor eigen sebagai sistem persamaan:

Mari kita alihkan semua istilah ke sebelah kiri:

Sistem terakhir boleh ditulis dalam bentuk matriks seperti berikut:

(A - lE)X \u003d O

Sistem yang terhasil sentiasa mempunyai penyelesaian sifar X = O. Sistem sedemikian di mana semua sebutan bebas adalah sama dengan sifar dipanggil homogen. Jika matriks sistem sedemikian adalah segi empat sama, dan penentunya tidak sama dengan sifar, maka mengikut formula Cramer, kita akan sentiasa mendapat penyelesaian unik - sifar. Ia boleh dibuktikan bahawa sistem mempunyai penyelesaian bukan sifar jika dan hanya jika penentu matriks ini sama dengan sifar, i.e.

|A - lE| = = 0

Persamaan dengan l yang tidak diketahui ini dipanggil persamaan ciri (polinomial ciri) matriks A (operator linear).

Ia boleh dibuktikan bahawa polinomial ciri pengendali linear tidak bergantung pada pilihan asas.

Sebagai contoh, mari kita cari nilai eigen dan vektor eigen bagi operator linear yang diberikan oleh matriks A = .

Untuk melakukan ini, kami menyusun persamaan ciri |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; nilai eigen l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

Untuk mencari vektor eigen, kita menyelesaikan dua sistem persamaan

(A + 5E) X = O

(A - 7E) X = O

Untuk yang pertama, matriks yang diperluaskan akan mengambil bentuk

dari mana x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, i.e. X (1) \u003d (- (2/3) s; s).

Untuk yang kedua daripada mereka, matriks yang diperluaskan akan mengambil bentuk

dari mana x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, i.e. X (2) \u003d ((2/3) s 1; s 1).

Oleh itu, vektor eigen pengendali linear ini ialah semua vektor bentuk (-(2/3)c; c) dengan nilai eigen (-5) dan semua vektor bentuk ((2/3)c 1 ; c 1) dengan nilai eigen 7 .

Ia boleh dibuktikan bahawa matriks pengendali A dalam asas yang terdiri daripada vektor eigennya adalah pepenjuru dan mempunyai bentuk:

di mana l i ialah nilai eigen bagi matriks ini.

Sebaliknya juga benar: jika matriks A dalam beberapa asas adalah pepenjuru, maka semua vektor asas ini akan menjadi vektor eigen bagi matriks ini.

Ia juga boleh dibuktikan bahawa jika pengendali linear mempunyai n nilai eigen berbeza berpasangan, maka vektor eigen yang sepadan adalah bebas linear, dan matriks operator ini dalam asas yang sepadan mempunyai bentuk pepenjuru.

Mari kita jelaskan ini dengan contoh sebelumnya. Mari kita ambil nilai bukan sifar sembarangan c dan c 1 , tetapi sedemikian rupa sehingga vektor X (1) dan X (2) adalah bebas linear, i.e. akan membentuk asas. Sebagai contoh, biarkan c \u003d c 1 \u003d 3, kemudian X (1) \u003d (-2; 3), X (2) \u003d (2; 3).

Mari kita sahkan kebebasan linear bagi vektor ini:

12 ≠ 0. Dalam asas baru ini, matriks A akan mengambil bentuk A * = .

Untuk mengesahkan ini, kami menggunakan formula A * = C -1 AC. Jom cari C -1 dulu.

C -1 = ;

Bentuk kuadratik

bentuk kuadratik f (x 1, x 2, xn) daripada n pembolehubah dipanggil jumlah, setiap sebutan adalah sama ada kuasa dua salah satu pembolehubah, atau hasil darab dua pembolehubah berbeza, diambil dengan pekali tertentu: f (x 1 , x 2, xn) = (a ij = a ji).

Matriks A, yang terdiri daripada pekali ini, dipanggil matriks bentuk kuadratik. Ia sentiasa simetri matriks (iaitu, matriks simetri tentang pepenjuru utama, a ij = a ji).

Dalam tatatanda matriks, bentuk kuadratik mempunyai bentuk f(X) = X T AX, di mana

Sesungguhnya

Sebagai contoh, mari kita tulis bentuk kuadratik dalam bentuk matriks.

Untuk melakukan ini, kita mencari matriks bentuk kuadratik. Unsur pepenjurunya adalah sama dengan pekali pada segi empat sama pembolehubah, dan unsur yang selebihnya adalah sama dengan separuh daripada pekali sepadan bentuk kuadratik. sebab tu

Biarkan lajur-matriks bagi pembolehubah X diperoleh dengan penjelmaan linear tak merosot bagi lajur-matriks Y, i.e. X = CY, dengan C ialah matriks tidak merosot tertib n. Kemudian bentuk kuadratik f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Oleh itu, di bawah penjelmaan linear tidak merosot C, matriks bentuk kuadratik mengambil bentuk: A * = C T AC.

Sebagai contoh, mari kita cari bentuk kuadratik f(y 1, y 2) yang diperoleh daripada bentuk kuadratik f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 dengan penjelmaan linear.

Bentuk kuadratik dipanggil berkanun(Ia mempunyai pandangan kanonik) jika semua pekalinya a ij = 0 untuk i ≠ j, i.e.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Matriksnya adalah pepenjuru.

Teorem(buktinya tidak diberikan di sini). Mana-mana bentuk kuadratik boleh dikurangkan kepada bentuk kanonik menggunakan penjelmaan linear tidak merosot.

Sebagai contoh, mari kita kurangkan kepada bentuk kanonik bentuk kuadratik
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Untuk melakukan ini, mula-mula pilih petak penuh untuk pembolehubah x 1:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2) ) 2 - 5x 2 2 - x 2 x 3.

Sekarang kita pilih petak penuh untuk pembolehubah x 2:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Kemudian penjelmaan linear tidak merosot y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 dan y 3 \u003d x 3 membawa bentuk kuadratik ini kepada bentuk kanonik f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Ambil perhatian bahawa bentuk kanonik bagi bentuk kuadratik ditakrifkan secara samar-samar (bentuk kuadratik yang sama boleh dikurangkan kepada bentuk kanonik dengan cara yang berbeza). Walau bagaimanapun, bentuk kanonik yang diperoleh dengan pelbagai kaedah mempunyai beberapa sifat umum. Khususnya, bilangan sebutan dengan pekali positif (negatif) bentuk kuadratik tidak bergantung pada cara bentuk itu dikurangkan kepada bentuk ini (contohnya, dalam contoh yang dipertimbangkan akan sentiasa ada dua pekali negatif dan satu positif). Sifat ini dipanggil hukum inersia bentuk kuadratik.

Mari kita sahkan ini dengan mengurangkan bentuk kuadratik yang sama kepada bentuk kanonik dengan cara yang berbeza. Mari kita mulakan transformasi dengan pembolehubah x 2:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, dengan y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6 ) x 3 dan y 3 = x 1 . Di sini, pekali negatif -3 pada y 1 dan dua pekali positif 3 dan 2 pada y 2 dan y 3 (dan menggunakan kaedah lain, kami mendapat pekali negatif (-5) pada y 2 dan dua pekali positif: 2 pada y 1 dan 1/20 untuk y 3).

Ia juga harus diperhatikan bahawa pangkat matriks bentuk kuadratik, dipanggil pangkat bentuk kuadratik, adalah sama dengan bilangan pekali bukan sifar bagi bentuk kanonik dan tidak berubah di bawah penjelmaan linear.

Bentuk kuadratik f(X) dipanggil secara positif (negatif) pasti, jika untuk semua nilai pembolehubah yang tidak serentak sama dengan sifar, ia adalah positif, i.e. f(X) > 0 (negatif, i.e.
f(X)< 0).

Sebagai contoh, bentuk kuadratik f 1 (X) \u003d x 1 2 + x 2 2 ialah pasti positif, kerana ialah hasil tambah kuasa dua, dan bentuk kuadratik f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 ialah negatif pasti, kerana mewakili ia boleh diwakili sebagai f 2 (X) \u003d - (x 1 - x 2) 2.

Dalam kebanyakan situasi praktikal, agak sukar untuk menetapkan kepastian tanda bagi bentuk kuadratik, jadi salah satu teorem berikut digunakan untuk ini (kami merumuskannya tanpa bukti).

Teorem. Bentuk kuadratik adalah positif (negatif) pasti jika dan hanya jika semua nilai eigen matriksnya adalah positif (negatif).

Teorem(Kriteria Sylvester). Bentuk kuadratik adalah pasti positif jika dan hanya jika semua minor utama bagi matriks bentuk ini adalah positif.

Major (sudut) kecil Susunan ke-k bagi matriks A bagi susunan ke-n dipanggil penentu matriks, terdiri daripada baris dan lajur k pertama bagi matriks A ().

Ambil perhatian bahawa untuk bentuk kuadratik pasti negatif, tanda-tanda minor utama silih berganti, dan minor urutan pertama mestilah negatif.

Sebagai contoh, kita meneliti bentuk kuadratik f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 untuk kepastian tanda.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. Oleh itu, bentuk kuadratik adalah pasti positif.

Kaedah 2. Minor utama bagi susunan pertama matriks AD 1 = a 11 = 2 > 0. Minor utama bagi susunan kedua D 2 = = 6 - 4 = 2 > 0. Oleh itu, mengikut kriteria Sylvester, bentuk kuadratik ialah pasti positif.

Kami memeriksa bentuk kuadratik lain untuk kepastian tanda, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Kaedah 1. Mari bina matriks bentuk kuadratik А = . Persamaan ciri akan mempunyai bentuk = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Oleh itu, bentuk kuadratik adalah pasti negatif.

Kaedah 2. Minor utama susunan pertama matriks A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Oleh itu, mengikut kriteria Sylvester, bentuk kuadratik adalah pasti negatif (tanda-tanda minor utama bergilir-gilir, bermula dari tolak).

Dan sebagai contoh lain, kita mengkaji bentuk kuadratik f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 untuk kepastian tanda.

Kaedah 1. Mari bina matriks bentuk kuadratik А = . Persamaan ciri akan mempunyai bentuk = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Satu daripada nombor ini adalah negatif dan satu lagi adalah positif. Tanda-tanda nilai eigen adalah berbeza. Oleh itu, bentuk kuadratik tidak boleh sama ada pasti negatif atau positif, i.e. bentuk kuadratik ini bukan tanda pasti (ia boleh mengambil nilai mana-mana tanda).

Kaedah 2. Minor utama susunan pertama matriks A D 1 = a 11 = 2 > 0. Minor utama susunan kedua D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).