Buat semua kemungkinan gabungan nombor dalam talian. Kombinatorik: peraturan dan formula asas

Mari kita pertimbangkan masalah mengira bilangan sampel daripada set tertentu dalam bentuk umum. Biar ada beberapa set N, yang terdiri daripada n elemen. Mana-mana subset yang terdiri daripada m elemen boleh dipertimbangkan tanpa mengambil kira susunannya, atau mengambil kiranya, i.e. apabila menukar pesanan, pindah ke yang lain m– persampelan.

Mari kita rumuskan definisi berikut:

Penempatan tanpa ulangan

Penempatan tanpa pengulangann unsur olehm Nmengandungimpelbagai elemen.

Daripada definisi itu, kedua-dua susunan berbeza antara satu sama lain, baik dalam unsur-unsurnya dan dalam susunannya, walaupun unsur-unsur itu sama.

Teorem 3. Bilangan peletakan tanpa pengulangan adalah sama dengan produk m faktor, yang terbesar adalah bilangannya n . Menulis:

Permutasi tanpa pengulangan

Permutasi daripadan elemen dipanggil susunan berbeza bagi setN.

Daripada takrifan ini, kedua-dua pilih atur hanya berbeza dalam susunan unsur dan ia boleh dianggap sebagai kes peletakan khas.

Teorem 4. Bilangan pilih atur berbeza tanpa pengulangan dikira dengan formula

Gabungan tanpa ulangan

Gabungan tanpa pengulangann unsur olehm sebarang subset tak tertib bagi suatu set dipanggilNmengandungim pelbagai elemen.

Daripada definisi itu, kedua-dua kombinasi itu hanya berbeza dalam unsur-unsur;

Teorem 5. Bilangan gabungan tanpa ulangan dikira menggunakan salah satu daripada formula berikut:

Contoh 1. Terdapat 5 kerusi di dalam bilik. Dalam berapa banyak cara anda boleh meletakkannya pada mereka?

a) 7 orang; b) 5 orang; c) 3 orang?

Penyelesaian: a) Pertama sekali, anda perlu memilih 5 orang daripada 7 orang untuk duduk di atas kerusi. Ia boleh dilakukan
cara. Dengan setiap pilihan lima tertentu, anda boleh menghasilkan
penyusunan semula. Mengikut teorem pendaraban, bilangan kaedah pendaratan yang diperlukan adalah sama.

Ulasan: Masalahnya boleh diselesaikan hanya menggunakan teorem produk, alasan seperti berikut: untuk tempat duduk di kerusi 1 terdapat 7 pilihan, di kerusi ke-2 terdapat 6 pilihan, pada ke-3 -5, pada ke-4 -4 dan pada 5- ke-3. Maka bilangan cara untuk menempatkan 7 orang di atas 5 kerusi ialah . Penyelesaian oleh kedua-dua kaedah adalah konsisten, kerana

b) Penyelesaiannya jelas -

V) - bilangan pemilihan kerusi yang diduduki.

- bilangan tempat duduk untuk tiga orang di atas tiga kerusi terpilih.

Jumlah pilihan raya ialah .

Tidak sukar untuk menyemak formula
;

;

Bilangan semua subset bagi suatu set yang terdiri daripada n elemen.

Ulang peletakan

Dengan meletakkan dengan pengulangan daripadan unsur olehm setiap subset tertib bagi suatu set dipanggilN, yang terdiri daripadam elemen supaya mana-mana elemen boleh dimasukkan dalam subset ini dari 1 hinggamkali, atau tidak hadir sama sekali.

Bilangan peletakan dengan pengulangan dilambangkan dengan dan dikira menggunakan formula, yang merupakan akibat daripada teorem pendaraban:

Contoh 2. Biarkan N = (a, b, c) menjadi set tiga huruf. Marilah kita memanggil mana-mana set huruf yang termasuk dalam set ini perkataan. Mari kita cari bilangan perkataan panjang 2 yang boleh dibuat daripada huruf ini:
.

Ulasan: Jelas sekali, peletakan dengan pengulangan juga boleh dipertimbangkan apabila
.

Contoh 3. Anda perlu menggunakan huruf (a, b) untuk mencipta semua perkataan yang mungkin panjangnya 3. Dalam berapa banyak cara ini boleh dilakukan?

Jawab:

Dalam artikel ini kita akan bercakap tentang satu cabang khas matematik yang dipanggil kombinatorik. Formula, peraturan, contoh penyelesaian masalah - anda boleh menemui semua ini di sini dengan membaca artikel hingga akhir.

Jadi apakah bahagian ini? Kombinatorik memperkatakan isu mengira sebarang objek. Tetapi dalam kes ini, objek bukan plum, pear atau epal, tetapi sesuatu yang lain. Kombinatorik membantu kita mencari kebarangkalian sesuatu peristiwa. Sebagai contoh, apabila bermain kad - apakah kebarangkalian bahawa pihak lawan mempunyai kad truf? Atau contoh ini: apakah kebarangkalian anda akan mendapat sebiji putih daripada beg dua puluh guli? Untuk masalah sebegini kita perlu tahu sekurang-kurangnya asas cabang matematik ini.

Konfigurasi gabungan

Memandangkan isu konsep asas dan formula kombinatorik, kami tidak boleh tidak memberi perhatian kepada konfigurasi gabungan. Mereka digunakan bukan sahaja untuk merumus, tetapi juga untuk menyelesaikan pelbagai contoh.

penginapan;
penyusunan semula;
gabungan;
komposisi nombor;
membelah nombor.

Kami akan bercakap tentang tiga yang pertama dengan lebih terperinci kemudian, tetapi kami akan memberi perhatian kepada komposisi dan pembahagian dalam bahagian ini. Apabila mereka bercakap tentang komposisi nombor tertentu (contohnya, a), mereka bermaksud mewakili nombor a sebagai jumlah tertib nombor positif tertentu. Dan partition ialah jumlah tidak tertib.

Bahagian

Sebelum kita beralih terus ke formula kombinatorik dan pertimbangan masalah, adalah wajar memberi perhatian kepada fakta bahawa kombinatorik, seperti cabang matematik lain, mempunyai subseksyen sendiri. Ini termasuk:

enumeratif;
struktur;
melampau;
teori Ramsey;
kebarangkalian;
topologi;
tak terhingga.

Dalam kes pertama, kita bercakap tentang kombinatorik pengiraan; masalah mempertimbangkan penghitungan atau pengiraan konfigurasi berbeza yang dibentuk oleh unsur set. Sebagai peraturan, beberapa sekatan dikenakan pada set ini (kebezaan, tidak dapat dibezakan, kemungkinan pengulangan, dan sebagainya). Dan bilangan konfigurasi ini dikira menggunakan peraturan penambahan atau pendaraban, yang akan kita bincangkan kemudian. Kombinatorik struktur merangkumi teori graf dan matroid. Contoh masalah kombinatorik ekstrem ialah apakah dimensi terbesar graf yang memenuhi sifat berikut... Dalam perenggan keempat, kami menyebut teori Ramsey, yang mengkaji kehadiran struktur biasa dalam konfigurasi rawak. Kombinatorik kebarangkalian mampu menjawab soalan - apakah kebarangkalian set tertentu mempunyai sifat tertentu. Seperti yang anda fikirkan, gabungan topologi menggunakan kaedah dalam topologi. Dan akhirnya, titik ketujuh - kombinatorik tak terhingga mengkaji penggunaan kaedah kombinatorik kepada set tak terhingga.

Peraturan tambahan

Di antara formula kombinatorik anda boleh menemui formula yang agak mudah, yang telah lama kita kenali. Contohnya ialah peraturan jumlah. Katakan kita diberi dua tindakan (C dan E), jika ia saling eksklusif, tindakan C boleh dilakukan dalam beberapa cara (contohnya, a), dan tindakan E boleh dilakukan dalam b-cara, maka mana-mana daripadanya ( C atau E) boleh dilakukan dengan cara a + b .

Secara teori, ini agak sukar untuk difahami; kami akan cuba menyampaikan keseluruhan perkara menggunakan contoh mudah. Mari kita ambil purata bilangan pelajar dalam satu kelas - katakan dua puluh lima. Antaranya ialah lima belas perempuan dan sepuluh lelaki. Seorang yang bertugas ditugaskan untuk setiap kelas setiap hari. Berapa banyak cara yang ada untuk melantik pemantau kelas hari ini? Penyelesaian kepada masalah ini agak mudah; kami akan menggunakan peraturan penambahan. Teks masalah tidak mengatakan bahawa hanya lelaki atau perempuan sahaja boleh bertugas. Oleh itu, boleh jadi mana-mana daripada lima belas perempuan atau mana-mana daripada sepuluh lelaki. Menggunakan peraturan jumlah, kita mendapat contoh yang agak mudah bahawa pelajar sekolah rendah boleh mengendalikan dengan mudah: 15 + 10. Selepas mengira, kita mendapat jawapan: dua puluh lima. Iaitu, hanya terdapat dua puluh lima cara untuk menetapkan kelas bertugas untuk hari ini.

Peraturan pendaraban

Formula asas kombinatorik juga termasuk peraturan pendaraban. Mari kita mulakan dengan teori. Katakan kita perlu melakukan beberapa tindakan (a): tindakan pertama dilakukan dalam 1 cara, yang kedua - dalam 2 cara, yang ketiga - dalam 3 cara, dan seterusnya sehingga tindakan a terakhir, dilakukan dalam 3 cara. Kemudian semua tindakan ini (yang kita ada jumlahnya) boleh dilakukan dalam N cara. Bagaimana untuk mengira N yang tidak diketahui? Formula akan membantu kita dengan ini: N = c1 * c2 * c3 *…* ca.

Sekali lagi, tiada yang jelas dalam teori, jadi mari kita teruskan untuk mempertimbangkan contoh mudah untuk menggunakan peraturan pendaraban. Mari kita ambil kelas yang sama dengan dua puluh lima orang, di mana terdapat lima belas perempuan dan sepuluh lelaki. Cuma kali ini kita perlu memilih dua orang yang bertugas. Mereka boleh menjadi lelaki atau perempuan, atau lelaki dan perempuan. Mari kita beralih kepada penyelesaian asas masalah. Kami memilih orang pertama yang bertugas, seperti yang kami putuskan dalam perenggan terakhir, kami mendapat dua puluh lima pilihan yang mungkin. Orang kedua yang bertugas boleh menjadi mana-mana orang yang tinggal. Kami mempunyai dua puluh lima pelajar, kami memilih seorang, yang bermaksud orang kedua yang bertugas boleh menjadi mana-mana daripada dua puluh empat orang yang tinggal. Akhirnya, kami menggunakan peraturan pendaraban dan mendapati dua pegawai yang bertugas boleh dipilih dalam enam ratus cara. Kami memperoleh nombor ini dengan mendarab dua puluh lima dan dua puluh empat.

Penyusunan semula

Sekarang kita akan melihat satu lagi formula kombinatorik. Dalam bahagian artikel ini kita akan bercakap tentang pilih atur. Kami mencadangkan untuk segera mempertimbangkan masalah menggunakan contoh. Mari kita ambil bola biliard, kita mempunyai nombor ke-n. Kita perlu mengira berapa banyak pilihan yang ada untuk menyusunnya secara berturut-turut, iaitu, untuk membuat set tersusun.

Mari kita mulakan, jika kita tidak mempunyai bola, maka kita juga mempunyai pilihan sifar untuk penempatan. Dan jika kita mempunyai satu bola, maka susunannya juga sama (secara matematik ini boleh ditulis seperti berikut: P1 = 1). Kedua-dua bola boleh diletakkan dalam dua cara yang berbeza: 1,2 dan 2,1. Oleh itu, P2 = 2. Tiga bola boleh disusun dalam enam cara (P3 = 6): 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,2,1; 3,1,2. Bagaimana jika tidak ada tiga bola seperti itu, tetapi sepuluh atau lima belas? Ia akan mengambil masa yang sangat lama untuk menyenaraikan semua pilihan yang mungkin, kemudian kombinatorik datang untuk membantu kami. Formula pilih atur akan membantu kita mencari jawapan kepada soalan yang menarik minat kita. Pn = n *P (n-1). Jika kita cuba untuk memudahkan formula, kita mendapat: Pn = n* (n - 1) *…* 2 * 1. Dan ini adalah hasil darab nombor asli pertama. Nombor ini dipanggil faktorial, dan dilambangkan sebagai n!

Mari kita pertimbangkan masalahnya. Setiap pagi kaunselor membariskan skuadnya (dua puluh orang). Terdapat tiga kawan baik dalam skuad - Kostya, Sasha dan Lesha. Apakah kebarangkalian bahawa mereka akan berdiri bersebelahan? Untuk mencari jawapan kepada soalan, anda perlu membahagikan kebarangkalian hasil yang "baik" dengan jumlah hasil. Jumlah bilangan pilih atur ialah 20! = 2.5 quintillion. Bagaimana untuk mengira bilangan hasil "baik"? Mari kita anggap bahawa Kostya, Sasha dan Lesha adalah seorang superman. Kemudian kami hanya mempunyai lapan belas mata pelajaran. Bilangan pilih atur dalam kes ini ialah 18 = 6.5 kuadrilion. Dengan semua ini, Kostya, Sasha dan Lesha boleh sewenang-wenangnya bergerak sesama mereka dalam tiga mereka yang tidak boleh dibahagikan, dan itu 3 lagi! = 6 pilihan. Ini bermakna kami mempunyai 18 pengaturan "baik" secara keseluruhan! * 3! Apa yang perlu kita lakukan ialah mencari kebarangkalian yang diingini: (18! * 3!) / 20! Yang bersamaan dengan lebih kurang 0.016. Jika ditukar kepada peratusan, ternyata hanya 1.6%.

Penginapan

Sekarang kita akan melihat satu lagi formula kombinatorik yang sangat penting dan perlu. Peletakan ialah keluaran kami yang seterusnya, yang kami menjemput anda untuk pertimbangkan dalam bahagian artikel ini. Kami akan mengalami komplikasi. Katakan kita ingin mempertimbangkan pilih atur yang mungkin, bukan daripada keseluruhan set (n), tetapi daripada yang lebih kecil (m). Iaitu, kami sedang mempertimbangkan pilih atur n item oleh m.

Formula asas kombinatorik bukan sahaja harus dihafal, tetapi difahami. Walaupun ia menjadi lebih rumit, kerana kita tidak mempunyai satu parameter, tetapi dua. Katakan bahawa m = 1, kemudian A = 1, m = 2, kemudian A = n * (n - 1). Jika kita memudahkan lagi formula dan beralih kepada notasi menggunakan faktorial, kita akan mendapat formula laconic sepenuhnya: A = n! / (n - m)!

Gabungan

Kami telah menyemak hampir semua formula kombinatorik asas dengan contoh. Sekarang mari kita beralih ke peringkat akhir mempertimbangkan kursus asas kombinatorik - mengenali kombinasi. Sekarang kita akan memilih m item daripada n yang kita ada, dan kita akan memilih segala-galanya dalam semua cara yang mungkin. Bagaimanakah ini berbeza daripada penempatan? Kami tidak akan mengambil kira pesanan. Set tidak tertib ini akan menjadi gabungan.

Marilah kita segera memperkenalkan tatatanda: C. Kami mengambil penempatan bola m daripada n. Kami berhenti memberi perhatian kepada pesanan dan berakhir dengan kombinasi berulang. Untuk mendapatkan bilangan gabungan kita perlu membahagikan bilangan peletakan dengan m! (m faktorial). Iaitu, C = A / m! Oleh itu, terdapat hanya beberapa cara untuk memilih daripada n bola, iaitu lebih kurang sama dengan bilangan cara untuk memilih hampir kesemuanya. Terdapat ungkapan logik untuk ini: memilih sedikit adalah sama dengan membuang hampir segala-galanya. Ia juga penting untuk menyebut pada ketika ini bahawa bilangan maksimum kombinasi boleh dicapai apabila cuba memilih separuh daripada item.

Bagaimana untuk memilih formula untuk menyelesaikan masalah?

Kami meneliti secara terperinci formula asas kombinatorik: penempatan, pilih atur dan gabungan. Sekarang tugas kami adalah untuk memudahkan pemilihan formula yang diperlukan untuk menyelesaikan masalah kombinatorik. Anda boleh menggunakan skema yang agak mudah berikut:

Tanya diri anda: adakah susunan elemen diletakkan diambil kira dalam teks masalah?
Jika jawapannya tidak, maka gunakan formula gabungan (C = n! / (m! * (n - m)!)).
Jika jawapannya tidak, maka soalan lain perlu dijawab: adakah semua elemen termasuk dalam gabungan?
Jika jawapannya ya, maka gunakan formula pilih atur (P = n!).
Jika jawapannya tidak, maka gunakan formula peletakan (A = n! / (n - m)!).

Contoh

Kami melihat unsur kombinatorik, formula dan beberapa isu lain. Sekarang mari kita teruskan untuk mempertimbangkan masalah sebenar. Bayangkan anda mempunyai kiwi, oren dan pisang di hadapan anda.

Soalan satu: dalam berapa banyak cara ia boleh disusun semula? Untuk melakukan ini, kami akan menggunakan formula pilih atur: P = 3! = 6 cara.

Soalan dua: dalam berapa banyak cara anda boleh memilih satu buah? Ini jelas, kita hanya mempunyai tiga pilihan - pilih kiwi, oren atau pisang, tetapi mari kita gunakan formula gabungan: C = 3! / (2! * 1!) = 3.

Soalan tiga: dalam berapa banyak cara anda boleh memilih dua buah? Apakah pilihan yang kita ada? kiwi dan oren; kiwi dan pisang; oren dan pisang. Iaitu, terdapat tiga pilihan, tetapi ini mudah untuk diperiksa menggunakan formula gabungan: C = 3! / (1! * 2!) = 3

Soalan empat: dalam berapa banyak cara anda boleh memilih tiga buah? Seperti yang anda lihat, hanya ada satu cara untuk memilih tiga buah: ambil kiwi, oren dan pisang. C = 3! / (0! * 3!) = 1.

Soalan lima: dalam berapa banyak cara anda boleh memilih sekurang-kurangnya satu buah? Syarat ini bermakna kita boleh mengambil satu, dua atau ketiga-tiga buah. Oleh itu, kita tambah C1 + C2 + C3 = 3 + 3 + 1 = 7. Iaitu, kita mempunyai tujuh cara untuk mengambil sekurang-kurangnya satu buah dari meja.

Perlu diingatkan bahawa kombinatorik adalah cabang bebas matematik yang lebih tinggi (dan bukan sebahagian daripada terver) dan buku teks yang berat telah ditulis mengenai disiplin ini, yang kandungannya, kadang-kadang, tidak lebih mudah daripada algebra abstrak. Walau bagaimanapun, sebahagian kecil pengetahuan teori akan mencukupi untuk kita, dan dalam artikel ini saya akan cuba menganalisis dalam bentuk yang boleh diakses asas-asas topik dengan masalah gabungan biasa. Dan ramai di antara anda akan membantu saya ;-)

Apa yang kita akan lakukan? Dalam erti kata yang sempit, kombinatorik ialah pengiraan pelbagai kombinasi yang boleh dibuat daripada set tertentu diskret objek. Objek difahami sebagai sebarang objek terpencil atau makhluk hidup - manusia, haiwan, cendawan, tumbuhan, serangga, dll. Pada masa yang sama, kombinatorik sama sekali tidak peduli bahawa set itu terdiri daripada pinggan bubur semolina, besi pematerian dan katak paya. Pada asasnya penting bahawa objek ini boleh disenaraikan - terdapat tiga daripadanya (kebijaksanaan) dan yang penting tiada satu pun daripada mereka yang serupa.

Kami telah menangani banyak perkara, sekarang mengenai kombinasi. Jenis gabungan yang paling biasa ialah pilih atur objek, pemilihannya daripada set (gabungan) dan pengedaran (peletakan). Mari lihat bagaimana ini berlaku sekarang:

Pilih atur, gabungan dan peletakan tanpa pengulangan

Jangan takut dengan istilah yang tidak jelas, terutamanya kerana sesetengahnya tidak begitu bagus. Mari kita mulakan dengan ekor tajuk - apa yang " tiada ulangan"? Ini bermakna dalam bahagian ini kita akan mempertimbangkan set yang terdiri daripada pelbagai objek. Sebagai contoh, ... tidak, saya tidak akan menawarkan bubur dengan besi pematerian dan katak, lebih baik ada yang lebih sedap =) Bayangkan sebiji epal, pear dan pisang telah menjelma di atas meja di hadapan anda ( jika anda mempunyai mereka, keadaan boleh disimulasikan dalam realiti). Kami meletakkan buah-buahan dari kiri ke kanan dalam susunan berikut:

epal / pir / pisang

Soalan satu: Dalam berapa banyak cara ia boleh disusun semula?

Satu kombinasi telah ditulis di atas dan tidak ada masalah dengan yang lain:

epal / pisang / pir
pir / epal / pisang
pir / pisang / epal
pisang / epal / pir
pisang / pir / epal

Jumlah: 6 kombinasi atau 6 pilih atur.

Okay, tidak sukar untuk menyenaraikan semua kemungkinan kes, tetapi bagaimana jika terdapat lebih banyak objek? Dengan hanya empat buah yang berbeza, bilangan gabungan akan meningkat dengan ketara!

Sila buka bahan rujukan (Ia mudah untuk mencetak manual) dan dalam titik No. 2, cari formula untuk bilangan pilih atur.

Tiada kerumitan - 3 objek boleh disusun semula dengan cara yang berbeza.

Soalan dua: Dalam berapa banyak cara anda boleh memilih a) satu buah, b) dua buah, c) tiga buah, d) sekurang-kurangnya satu buah?

Kenapa pilih? Jadi kami menaikkan selera dalam perenggan sebelumnya - untuk makan! =)

a) Satu buah boleh dipilih, jelas, dalam tiga cara - ambil sama ada epal, pir, atau pisang. Pengiraan formal dijalankan mengikut formula untuk bilangan gabungan:

Entri dalam kes ini harus difahami seperti berikut: "dalam berapa banyak cara anda boleh memilih 1 buah daripada tiga?"

b) Mari kita senaraikan semua kemungkinan gabungan dua buah:

epal dan pir;
epal dan pisang;
pir dan pisang.

Bilangan kombinasi boleh disemak dengan mudah menggunakan formula yang sama:

Entri itu difahami dengan cara yang sama: "dalam berapa banyak cara anda boleh memilih 2 buah daripada tiga?"

c) Dan akhirnya, hanya ada satu cara untuk memilih tiga buah:

Ngomong-ngomong, formula untuk bilangan kombinasi kekal bermakna untuk sampel kosong:
Dengan cara ini, anda tidak boleh memilih satu buah - sebenarnya, tidak mengambil apa-apa dan itu sahaja.

d) Berapa banyak cara yang boleh anda ambil sekurang-kurangnya satu buah? Syarat "sekurang-kurangnya satu" menunjukkan bahawa kita berpuas hati dengan 1 buah (mana-mana) atau mana-mana 2 buah atau kesemua 3 buah:
menggunakan kaedah ini anda boleh memilih sekurang-kurangnya satu buah.

Pembaca yang telah mempelajari dengan teliti pelajaran pengenalan tentang teori kebarangkalian, kami sudah meneka sesuatu. Tetapi lebih lanjut mengenai maksud tanda tambah nanti.

Untuk menjawab soalan seterusnya saya memerlukan dua sukarelawan... ...Nah, kerana tiada siapa yang mahu, maka saya akan memanggil anda ke lembaga =)

Soalan tiga: Dalam beberapa cara anda boleh mengedarkan satu buah setiap satu kepada Dasha dan Natasha?

Untuk mengedarkan dua buah, anda perlu memilihnya terlebih dahulu. Menurut perenggan "menjadi" soalan sebelumnya, ini boleh dilakukan dengan cara, saya akan menulis semula:

epal dan pir;
epal dan pisang;
pir dan pisang.

Tetapi kini akan terdapat dua kali lebih banyak kombinasi. Pertimbangkan, sebagai contoh, sepasang buah pertama:
Anda boleh merawat Dasha dengan epal, dan Natasha dengan pir;
atau sebaliknya - Dasha akan mendapat pir, dan Natasha akan mendapat epal.

Dan pilih atur sedemikian mungkin untuk setiap pasangan buah.

Pertimbangkan kumpulan pelajar yang sama yang pergi ke tarian itu. Dalam berapa banyak cara seorang lelaki dan perempuan boleh digandingkan?

Dengan cara anda boleh memilih 1 lelaki muda;
cara anda boleh memilih 1 perempuan.

Oleh itu, seorang pemuda Dan Anda boleh memilih seorang gadis: cara.

Apabila 1 objek dipilih daripada setiap set, prinsip berikut untuk mengira kombinasi adalah sah: “ setiap objek daripada satu set boleh membentuk pasangan dengan setiap objek set lain."

Iaitu, Oleg boleh menjemput mana-mana daripada 13 gadis untuk menari, Evgeny juga boleh menjemput mana-mana daripada tiga belas, dan orang muda yang lain mempunyai pilihan yang sama. Jumlah: pasangan yang mungkin.

Perlu diingatkan bahawa dalam contoh ini, "sejarah" pembentukan pasangan itu tidak penting; namun, jika kita mengambil kira inisiatif itu, bilangan gabungan mesti digandakan, kerana setiap daripada 13 gadis itu juga boleh menjemput mana-mana lelaki untuk menari. Semuanya bergantung pada syarat tugas tertentu!

Prinsip yang sama adalah sah untuk kombinasi yang lebih kompleks, sebagai contoh: dalam berapa banyak cara anda boleh memilih dua lelaki muda? Dan dua gadis untuk mengambil bahagian dalam skit KVN?

Kesatuan DAN jelas menunjukkan bahawa kombinasi perlu didarabkan:

Kumpulan artis yang mungkin.

Dalam kata lain, setiap satu sepasang lelaki (45 pasangan unik) boleh membuat persembahan dengan mana-mana sepasang perempuan (78 pasangan unik). Dan jika kita mempertimbangkan pengagihan peranan antara peserta, akan ada lebih banyak kombinasi. ... Saya benar-benar mahu, tetapi saya akan tetap menahan diri daripada meneruskan supaya tidak menanamkan dalam diri anda kebencian terhadap kehidupan pelajar =).

Peraturan untuk mendarab gabungan juga terpakai kepada bilangan pengganda yang lebih besar:

Masalah 8

Berapakah bilangan nombor tiga digit yang boleh dibahagi dengan 5?

Penyelesaian: untuk kejelasan, mari kita nyatakan nombor ini dengan tiga asterisk: ***

DALAM ratusan tempat Anda boleh menulis mana-mana nombor (1, 2, 3, 4, 5, 6, 7, 8 atau 9). Sifar tidak sesuai, kerana dalam kes ini bilangannya tidak lagi menjadi tiga digit.

Tetapi dalam tempat berpuluh-puluh(“di tengah”) anda boleh memilih mana-mana daripada 10 digit: .

Mengikut syarat, nombor mesti boleh dibahagi dengan 5. Nombor boleh dibahagi dengan 5 jika ia berakhir dengan 5 atau 0. Oleh itu, kita berpuas hati dengan 2 digit dalam digit terkecil.

Secara keseluruhan, ada: nombor tiga digit yang boleh dibahagi dengan 5.

Dalam kes ini, kerja itu ditafsirkan seperti berikut: “9 cara anda boleh memilih nombor dalam ratusan tempat Dan 10 cara untuk memilih nombor dalam tempat berpuluh-puluh Dan 2 cara masuk digit unit»

Atau lebih mudah lagi: “ setiap satu daripada 9 digit kepada ratusan tempat menggabungkan dengan masing-masing daripada 10 digit tempat berpuluh-puluh dan dengan masing-masing daripada dua digit kepada digit unit».

Jawab: 180

Dan sekarang…

Ya, saya hampir terlupa tentang ulasan yang dijanjikan mengenai masalah No. 5, di mana Bor, Dima dan Volodya boleh diberikan satu kad setiap satu dengan cara yang berbeza. Pendaraban di sini mempunyai makna yang sama: cara untuk mengeluarkan 3 kad dari dek DAN dalam setiap sampel menyusun semula mereka dengan cara.

Dan kini masalah untuk diselesaikan sendiri... sekarang saya akan tampil dengan sesuatu yang lebih menarik... biarlah mengenai versi blackjack Rusia yang sama:

Masalah 9

Berapa banyak kombinasi kemenangan 2 kad yang ada semasa bermain "mata"?

Bagi mereka yang tidak tahu: kombinasi yang menang ialah 10 + ACE (11 mata) = 21 mata dan, mari kita pertimbangkan gabungan kemenangan dua ace.

(urutan kad dalam mana-mana pasangan tidak penting)

Penyelesaian ringkas dan jawapan pada akhir pelajaran.

By the way, jangan anggap contoh primitif. Blackjack adalah hampir satu-satunya permainan yang mempunyai algoritma berasaskan matematik yang membolehkan anda mengalahkan kasino. Mereka yang berminat boleh mencari banyak maklumat tentang strategi dan taktik optimum dengan mudah. Benar, tuan-tuan seperti itu agak cepat berakhir dalam senarai hitam semua pertubuhan =)

Sudah tiba masanya untuk menyatukan bahan yang diliputi dengan beberapa tugas yang kukuh:

Masalah 10

Vasya mempunyai 4 ekor kucing di rumah.

a) berapakah cara kucing boleh duduk di sudut-sudut bilik?
b) dalam berapa banyak cara anda boleh membiarkan kucing berjalan-jalan?
c) dalam berapa banyak cara Vasya boleh mengambil dua kucing (satu di sebelah kirinya, satu lagi di sebelah kanannya)?

Mari buat keputusan: pertama sekali, anda perlu sekali lagi memberi perhatian kepada fakta bahawa masalah itu ditangani berbeza objek (walaupun kucing adalah kembar seiras). Ini adalah syarat yang sangat penting!

a) Mendiamkan kucing. Tertakluk kepada pelaksanaan ini semua kucing sekali gus
+ lokasi mereka adalah penting, jadi terdapat pilih atur di sini:
menggunakan kaedah ini anda boleh meletakkan kucing di sudut bilik.

Saya ulangi bahawa apabila mengubah suai, hanya bilangan objek yang berbeza dan kedudukan relatifnya yang penting. Bergantung pada moodnya, Vasya boleh meletakkan haiwan dalam separuh bulatan di atas sofa, berturut-turut di ambang tingkap, dll. – dalam semua kes akan terdapat 24 pilih atur Untuk kemudahan, mereka yang berminat boleh membayangkan bahawa kucing adalah pelbagai warna (contohnya, putih, hitam, merah dan berkutik) dan senaraikan semua kombinasi yang mungkin.

b) Dalam beberapa cara anda boleh membiarkan kucing berjalan-jalan?

Diandaikan bahawa kucing pergi berjalan-jalan hanya melalui pintu, dan soalan itu membayangkan sikap acuh tak acuh mengenai bilangan haiwan - 1, 2, 3 atau semua 4 kucing boleh berjalan-jalan.

Kami mengira semua kombinasi yang mungkin:

Dengan cara ini anda boleh membiarkan seekor kucing (mana-mana daripada empat) pergi berjalan-jalan;
cara anda boleh membiarkan dua kucing berjalan-jalan (senarai sendiri pilihan);
dengan cara anda boleh membiarkan tiga kucing berjalan-jalan (salah satu daripada empat kucing itu duduk di rumah);
Dengan cara ini anda boleh melepaskan semua kucing.

Anda mungkin meneka bahawa nilai yang terhasil harus disimpulkan:
cara anda boleh membiarkan kucing berjalan-jalan.

Untuk peminat, saya menawarkan versi masalah yang rumit - apabila mana-mana kucing dalam mana-mana sampel boleh keluar secara rawak, melalui pintu dan melalui tingkap di tingkat 10. Akan ada peningkatan ketara dalam kombinasi!

c) Dalam berapa banyak cara Vasya boleh mengambil dua ekor kucing?

Situasi ini melibatkan bukan sahaja memilih 2 haiwan, tetapi juga meletakkannya di setiap tangan:
Dengan cara ini anda boleh mengambil 2 ekor kucing.

Penyelesaian kedua: anda boleh memilih dua kucing menggunakan kaedah Dan cara-cara menanam setiap pasangan di tangan:

Jawab: a) 24, b) 15, c) 12

Nah, untuk membersihkan hati nurani anda, sesuatu yang lebih khusus tentang penggandaan gabungan... Biarkan Vasya mempunyai 5 ekor kucing tambahan =) Dalam berapa banyak cara anda boleh membiarkan 2 ekor kucing berjalan-jalan? Dan 1 kucing?

Iaitu, dengan setiap satu sepasang kucing boleh dilepaskan setiap kucing.

Satu lagi butang akordion untuk penyelesaian bebas:

Masalah 11

3 penumpang menaiki lif bangunan 12 tingkat. Semua orang, tanpa mengira yang lain, boleh keluar di mana-mana (bermula dari tingkat 2) dengan kebarangkalian yang sama. Dalam berapa banyak cara:

1) penumpang boleh turun di tingkat yang sama (perintah keluar tidak penting);
2) dua orang boleh turun di satu tingkat, dan yang ketiga di tingkat yang lain;
3) orang boleh keluar di tingkat yang berbeza;
4) bolehkah penumpang keluar dari lif?

Dan di sini mereka sering bertanya lagi, saya jelaskan: jika 2 atau 3 orang keluar di tingkat yang sama, maka perintah keluar tidak penting. FIKIRKAN, gunakan formula dan peraturan untuk menambah/mendarab gabungan. Sekiranya terdapat kesukaran, adalah berguna bagi penumpang untuk memberikan nama dan membuat spekulasi dalam kombinasi yang mereka boleh keluar dari lif. Tidak perlu gusar jika ada yang tidak berjaya, sebagai contoh, titik No. 2 agak berbahaya.

Penyelesaian penuh dengan ulasan terperinci pada akhir pelajaran.

Perenggan akhir dikhaskan untuk kombinasi yang juga berlaku agak kerap - menurut penilaian subjektif saya, dalam kira-kira 20-30% masalah gabungan:

Pilih atur, gabungan dan peletakan dengan ulangan

Jenis gabungan yang disenaraikan digariskan dalam perenggan No. 5 bahan rujukan Formula asas kombinatorik, walau bagaimanapun, sesetengah daripadanya mungkin tidak begitu jelas pada bacaan pertama. Dalam kes ini, pertama sekali dinasihatkan untuk membiasakan diri dengan contoh praktikal, dan hanya kemudian memahami rumusan umum. Pergi:

Pilih atur dengan ulangan

Dalam pilih atur dengan ulangan, seperti dalam pilih atur "biasa", semua objek yang banyak sekali gus, tetapi ada satu perkara: dalam set ini satu atau lebih elemen (objek) diulang. Memenuhi piawaian seterusnya:

Masalah 12

Berapa banyak kombinasi huruf yang berbeza boleh diperolehi dengan menyusun semula kad dengan huruf berikut: K, O, L, O, K, O, L, b, Ch, I, K?

Penyelesaian: sekiranya semua huruf berbeza, maka formula remeh perlu digunakan, tetapi jelas sekali bahawa untuk set kad yang dicadangkan beberapa manipulasi akan berfungsi "secara terbiar", contohnya, jika anda menukar mana-mana dua kad dengan huruf “K” " dalam sebarang perkataan, anda mendapat perkataan yang sama. Selain itu, secara fizikal kad boleh sangat berbeza: satu boleh bulat dengan huruf "K" dicetak di atasnya, satu lagi boleh segi empat sama dengan huruf "K" dilukis di atasnya. Tetapi mengikut maksud tugas, walaupun kad sedemikian dianggap sama, kerana syaratnya bertanya tentang gabungan huruf.

Segala-galanya sangat mudah - hanya 11 kad, termasuk surat:

K - diulang 3 kali;
O - diulang 3 kali;
L - diulang 2 kali;
b – diulang 1 kali;
H - diulang 1 kali;
Dan - diulang 1 kali.

Semak: 3 + 3 + 2 + 1 + 1 + 1 = 11, iaitu perkara yang perlu disemak.

Mengikut formula bilangan pilih atur dengan ulangan:
kombinasi huruf yang berbeza boleh diperolehi. Lebih daripada setengah juta!

Untuk mengira nilai faktorial yang besar dengan cepat, adalah mudah untuk menggunakan fungsi Excel standard: masukkan ke dalam mana-mana sel =FAKTA(11) dan tekan Masuk.

Dalam amalan, agak boleh diterima untuk tidak menulis formula am dan, sebagai tambahan, untuk meninggalkan faktorial unit:

Tetapi ulasan awal tentang surat berulang diperlukan!

Jawab: 554400

Satu lagi contoh biasa pilih atur dengan pengulangan berlaku dalam masalah peletakan buah catur, yang boleh didapati di gudang penyelesaian siap sedia dalam pdf yang sepadan. Dan untuk penyelesaian bebas, saya menghasilkan tugas yang kurang formula:

Masalah 13

Alexey pergi bersukan, dan 4 hari seminggu - olahraga, 2 hari - senaman kekuatan dan 1 hari berehat. Dalam berapa banyak cara dia boleh membuat jadual mingguan untuk dirinya sendiri?

Formula tidak berfungsi di sini kerana ia mengambil kira pertukaran kebetulan (contohnya, menukar latihan kekuatan hari Rabu dengan latihan kekuatan hari Khamis). Dan sekali lagi - sebenarnya, 2 sesi latihan kekuatan yang sama boleh sangat berbeza antara satu sama lain, tetapi dalam konteks tugas (dari sudut pandangan jadual) mereka dianggap elemen yang sama.

Penyelesaian dua baris dan jawab pada akhir pelajaran.

Gabungan dengan pengulangan

Ciri ciri gabungan jenis ini ialah sampel diambil daripada beberapa kumpulan, setiap satunya terdiri daripada objek yang serupa.

Semua orang telah bekerja keras hari ini, jadi sudah tiba masanya untuk menyegarkan diri anda:

Masalah 14

Kantin pelajar menjual sosej dalam doh, kek keju dan donat. Dalam berapa banyak cara anda boleh membeli lima pai?

Penyelesaian: segera beri perhatian kepada kriteria tipikal untuk kombinasi dengan pengulangan - mengikut syarat, ia bukan satu set objek seperti yang ditawarkan untuk pilihan, tetapi jenis lain objek; diandaikan terdapat sekurang-kurangnya lima hot dog, 5 kek keju dan 5 donat dijual. Pai dalam setiap kumpulan, sudah tentu, berbeza - kerana donat yang sama sekali hanya boleh disimulasikan pada komputer =) Walau bagaimanapun, ciri fizikal pai tidak penting untuk tujuan masalah, dan hot dog / kek keju / donat dalam kumpulan mereka dianggap sama.

Apa yang mungkin ada dalam sampel? Pertama sekali, perlu diingatkan bahawa pasti akan ada pai yang sama dalam sampel (kerana kami memilih 5 keping, dan terdapat 3 jenis untuk dipilih). Terdapat pilihan di sini untuk setiap citarasa: 5 hot dog, 5 kek keju, 5 donat, 3 hot dog + 2 kek keju, 1 hot dog + 2 kek keju + 2 donat, dsb.

Seperti kombinasi "biasa", susunan pemilihan dan peletakan pai dalam pemilihan tidak penting - anda hanya memilih 5 keping dan itu sahaja.

Kami menggunakan formula bilangan kombinasi dengan ulangan:
Anda boleh membeli 5 pai menggunakan kaedah ini.

Selamat menjamu selera!

Jawab: 21

Apakah kesimpulan yang boleh dibuat daripada banyak masalah gabungan?

Kadang-kadang perkara yang paling sukar ialah memahami keadaan.

Contoh yang sama untuk penyelesaian bebas:

Masalah 15

Dompet itu mengandungi sejumlah besar syiling 1-, 2-, 5- dan 10-ruble. Dalam berapa banyak cara tiga syiling boleh dikeluarkan dari dompet?

Untuk tujuan kawalan diri, jawab beberapa soalan mudah:

1) Bolehkah semua syiling dalam sampel berbeza?
2) Namakan gabungan syiling yang "paling murah" dan "mahal".

Penyelesaian dan jawapan pada akhir pelajaran.

Dari pengalaman peribadi saya, saya boleh mengatakan bahawa kombinasi dengan ulangan adalah tetamu paling jarang dalam amalan, yang tidak boleh dikatakan tentang jenis gabungan berikut:

Penempatan dengan ulangan

Daripada set yang terdiri daripada elemen, elemen dipilih, dan susunan elemen dalam setiap pemilihan adalah penting. Dan semuanya akan baik-baik saja, tetapi jenaka yang agak tidak dijangka ialah kita boleh memilih mana-mana objek set asal seberapa banyak yang kita mahu. Secara kiasan, “orang ramai tidak akan berkurangan”.

Bilakah ini berlaku? Contoh biasa ialah kunci gabungan dengan beberapa cakera, tetapi disebabkan perkembangan teknologi, adalah lebih relevan untuk mempertimbangkan keturunan digitalnya:

Masalah 16

Berapakah bilangan kod PIN empat digit?

Penyelesaian: sebenarnya, untuk menyelesaikan masalah, pengetahuan tentang peraturan kombinatorik sudah cukup: dengan cara anda boleh memilih digit pertama kod PIN Dan cara - digit kedua kod PIN Dan dalam banyak cara - ketiga Dan nombor yang sama - keempat. Oleh itu, mengikut peraturan mendarab gabungan, kod pin empat digit boleh digubah dalam: cara.

Dan kini menggunakan formula. Mengikut syarat, kami ditawarkan satu set nombor, dari mana nombor dipilih dan disusun dalam susunan tertentu, manakala nombor dalam sampel mungkin diulang (iaitu mana-mana digit set asal boleh digunakan sewenang-wenangnya beberapa kali). Mengikut formula untuk bilangan peletakan dengan ulangan:

Jawab: 10000

Apa yang terlintas di fikiran di sini... ...jika ATM "memakan" kad itu selepas percubaan ketiga yang tidak berjaya untuk memasukkan kod PIN, maka peluang untuk mengambilnya secara rawak adalah sangat tipis.

Dan siapa yang mengatakan bahawa kombinatorik tidak mempunyai makna praktikal? Tugas kognitif untuk semua pembaca tapak:

Masalah 17

Mengikut piawaian negeri, plat lesen kereta terdiri daripada 3 nombor dan 3 huruf. Dalam kes ini, nombor dengan tiga sifar tidak boleh diterima dan huruf dipilih daripada set A, B, E, K, M, N, O, P, S, T, U, X (hanya huruf Cyrillic yang digunakan yang ejaannya bertepatan dengan huruf Latin).

Berapakah bilangan plat lesen yang berbeza boleh dibuat untuk sesuatu wilayah?

Tidak banyak daripada mereka, dengan cara itu. Di kawasan besar tidak ada kuantiti sedemikian, dan oleh itu bagi mereka terdapat beberapa kod untuk inskripsi RUS.

Penyelesaian dan jawapan ada pada akhir pelajaran. Jangan lupa gunakan peraturan kombinatorik ;-) ...Saya ingin menunjukkan apa yang eksklusif, tetapi ternyata tidak eksklusif =) Saya melihat Wikipedia - ada pengiraan di sana, walaupun tanpa ulasan. Walaupun untuk tujuan pendidikan, mungkin hanya sedikit orang yang menyelesaikannya.

Pelajaran menarik kami telah berakhir, dan akhirnya saya ingin mengatakan bahawa anda tidak membuang masa anda - atas sebab formula kombinatorik mencari satu lagi aplikasi praktikal yang penting: ia ditemui dalam pelbagai masalah dalam teori kebarangkalian,
dan dalam masalah yang melibatkan penentuan klasik kebarangkalian– selalunya =)

Terima kasih semua atas penyertaan aktif anda dan jumpa lagi!

Penyelesaian dan Jawapan:

Tugasan 2: Penyelesaian: cari nombor semua pilih atur yang mungkin bagi 4 kad:

Apabila kad dengan sifar diletakkan di tempat pertama, nombor itu menjadi tiga digit, jadi gabungan ini harus dikecualikan. Biarkan sifar berada di tempat pertama, kemudian baki 3 digit dalam digit bawah boleh disusun semula dengan cara yang berbeza.

Catatan : sebab Memandangkan hanya terdapat beberapa kad, mudah untuk menyenaraikan semua pilihan di sini:
0579
0597
0759
0795
0957
0975

Oleh itu, dari set yang dicadangkan kita boleh membuat:
24 – 6 = 18 nombor empat digit
Jawab : 18

Tugasan 4: Penyelesaian: dengan cara anda boleh memilih 3 kad daripada 36.
Jawab : 7140

Tugasan 6: Penyelesaian: cara.
Satu lagi penyelesaian : cara anda boleh memilih dua orang daripada kumpulan dan dan
2) Set "paling murah" mengandungi 3 syiling ruble, dan yang paling "mahal" - 3 syiling sepuluh ruble.

Masalah 17: Penyelesaian: menggunakan kaedah ini, anda boleh mencipta gabungan digital plat lesen kereta, dan salah satu daripadanya (000) harus dikecualikan: .
menggunakan kaedah ini, anda boleh membuat gabungan huruf nombor plat lesen.
Mengikut peraturan gabungan pendaraban, jumlah boleh dibuat:
plat lesen
(setiap satu gabungan digital digabungkan dengan masing-masing gabungan huruf).
Jawab : 1726272

Mari kita mengira dalam MS EXCEL bilangan gabungan n elemen dengan k. Menggunakan formula, kami akan memaparkan pada helaian semua varian gabungan (terjemahan bahasa Inggeris bagi istilah: Gabungan tanpa pengulangan).

Gabungan n unsur berbeza unsur k ialah gabungan yang berbeza dalam sekurang-kurangnya satu unsur. Sebagai contoh, di bawah adalah SEMUA gabungan 3 elemen yang diambil daripada set yang terdiri daripada 5 elemen (1; 2; 3; 4; 5):

(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)

Catatan: Ini ialah artikel tentang mengira bilangan gabungan menggunakan MS EXCEL. Kami mengesyorkan membaca asas teori dalam buku teks khusus. Mempelajari gabungan daripada artikel ini adalah idea yang tidak baik.

Perbezaan antara Gabungan dan Peletakan

Memaparkan semua gabungan Gabungan

Dalam fail contoh, formula dicipta untuk memaparkan semua Gabungan bagi n dan k yang diberikan.

Dengan menyatakan bilangan elemen set (n) dan bilangan elemen yang kita pilih daripadanya (k), menggunakan formula kita boleh memaparkan semua Gabungan.

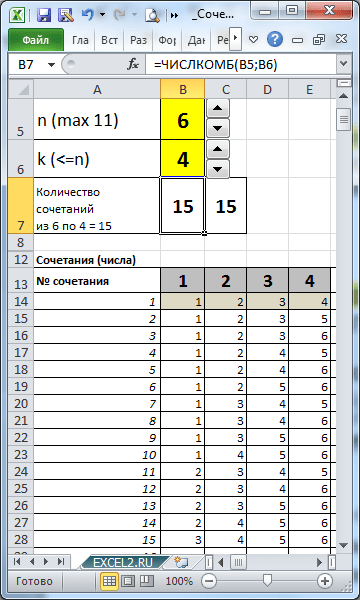
Tugasan

Pengangkut kereta boleh mengangkut 4 buah kereta. Ia adalah perlu untuk mengangkut 7 kereta yang berbeza (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Dalam berapa banyak cara berbeza pengangkut kereta pertama boleh diisi? Tempat khusus kereta dalam pengangkut kereta tidak penting.

Kita perlu menentukan nombor Gabungan 7 kereta di 4 tempat pengangkut kereta. Itu. n=7, dan k=4. Ternyata terdapat 35 pilihan tersebut =NUMBERCOMB(7,4).