Zoek de eigenwaarden van de operator. Eigenwaarden (getallen) en eigenvectoren Voorbeelden van oplossingen

Diagonale matrices hebben de eenvoudigste structuur. De vraag rijst of het mogelijk is een basis te vinden waarin de matrix van de lineaire operator een diagonale vorm zou hebben. Een dergelijke basis bestaat.
Laten we een lineaire ruimte R n krijgen en een lineaire operator A die daarin werkt; in dit geval neemt operator A R n in zichzelf, dat wil zeggen A:R n → R n .

Definitie. Een vector die niet nul is, wordt een eigenvector van operator A genoemd als operator A zich vertaalt in een collineaire vector. Het getal λ wordt de eigenwaarde of eigenwaarde van de operator A genoemd, overeenkomend met de eigenvector.
Laten we enkele eigenschappen van eigenwaarden en eigenvectoren noteren.
1. Elke lineaire combinatie van eigenvectoren operator A die overeenkomt met dezelfde eigenwaarde λ is een eigenvector met dezelfde eigenwaarde.
2. Eigenvectoren operator A met paarsgewijs verschillende eigenwaarden λ 1 , λ 2 , …, λ m zijn lineair onafhankelijk.
3. Als de eigenwaarden λ 1 =λ 2 = λ m = λ, dan komt de eigenwaarde λ overeen met niet meer dan m lineair onafhankelijke eigenvectoren.

Dus als er n lineair onafhankelijke eigenvectoren zijn , overeenkomend met verschillende eigenwaarden λ 1, λ 2, ..., λ n, dan zijn ze lineair onafhankelijk, daarom kunnen ze worden genomen als de basis van de ruimte R n. Laten we de vorm van de matrix van de lineaire operator A vinden op basis van zijn eigenvectoren, waarvoor we met de operator A zullen werken op basis van de basisvectoren: Dan .
De matrix van de lineaire operator A heeft dus op basis van zijn eigenvectoren een diagonale vorm en de eigenwaarden van de operator A liggen langs de diagonaal.
Is er een andere basis waarin de matrix een diagonale vorm heeft? Het antwoord op deze vraag wordt gegeven door de volgende stelling.

Stelling. De matrix van een lineaire operator A in de basis (i = 1..n) heeft een diagonale vorm dan en slechts dan als alle vectoren van de basis eigenvectoren zijn van de operator A.

Regel voor het vinden van eigenwaarden en eigenvectoren

. (*)

(1)
Waar - lineaire operatormatrix.

Systeem (1) heeft een oplossing die niet nul is als de determinant D gelijk is aan nul

Voorbeeld 12. De lineaire operator A werkt in R 3 volgens de wet, waarbij x 1, x 2, .., x n de coördinaten zijn van de vector in de basis , , . Zoek de eigenwaarden en eigenvectoren van deze operator.
Oplossing. We bouwen de matrix van deze operator:
.
We creëren een systeem voor het bepalen van de coördinaten van eigenvectoren:

We stellen een karakteristieke vergelijking samen en lossen deze op:

.
λ 1,2 = -1, λ 3 = 3.
Als we λ = -1 in het systeem vervangen, krijgen we:
of
Omdat , dan zijn er twee afhankelijke variabelen en één vrije variabele.
Laat x 1 dan een vrije onbekende zijn We lossen dit systeem op welke manier dan ook op en vinden de algemene oplossing van dit systeem: Het fundamentele systeem van oplossingen bestaat uit één oplossing, aangezien n - r = 3 - 2 = 1.
De set eigenvectoren die overeenkomt met de eigenwaarde λ = -1 heeft de vorm: , waarbij x 1 een ander getal dan nul is. Laten we één vector uit deze set kiezen, bijvoorbeeld door x 1 = 1 te plaatsen: .
Op dezelfde manier redeneren we dat de eigenvector overeenkomt met de eigenwaarde λ = 3: .
In de ruimte R 3 bestaat de basis uit drie lineair onafhankelijke vectoren, maar we ontvingen slechts twee lineair onafhankelijke eigenvectoren, waaruit de basis in R 3 niet kan worden samengesteld. Bijgevolg kunnen we de matrix A van een lineaire operator niet reduceren tot een diagonale vorm.

Voorbeeld 13. Gegeven een matrix .
1. Bewijs dat de vector is een eigenvector van matrix A. Zoek de eigenwaarde die overeenkomt met deze eigenvector.
2. Zoek een basis waarin matrix A een diagonale vorm heeft.
Oplossing.
1. Als , dan is een eigenvector

.
Vector (1, 8, -1) is een eigenvector. Eigenwaarde λ = -1.
De matrix heeft een diagonale vorm in een basis bestaande uit eigenvectoren. Eén ervan is beroemd. Laten we de rest zoeken.
We zoeken naar eigenvectoren uit het systeem:

Karakteristieke vergelijking: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Laten we de eigenvector vinden die overeenkomt met de eigenwaarde λ = -3:

De rang van de matrix van dit systeem is twee en gelijk aan het aantal onbekenden, dus dit systeem heeft alleen een nuloplossing x 1 = x 3 = 0. x 2 kan hier alles anders zijn dan nul, bijvoorbeeld x 2 = 1. De vector (0 ,1,0) is dus een eigenvector die overeenkomt met λ = -3. Laten we het controleren:
.
Als λ = 1, dan verkrijgen we het systeem
De rang van de matrix is ​​twee. We schrappen de laatste vergelijking.
Laat x 3 een vrije onbekende zijn. Dan x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Ervan uitgaande dat x 3 = 1, hebben we (-3,-9,1) - een eigenvector die overeenkomt met de eigenwaarde λ = 1. Controleer:

.
Omdat de eigenwaarden reëel en verschillend zijn, zijn de ermee corresponderende vectoren lineair onafhankelijk, zodat ze als basis in R 3 kunnen worden genomen. In de basis dus , , matrix A heeft de vorm:
.
Niet elke matrix van een lineaire operator A:R n → R n kan worden gereduceerd tot een diagonale vorm, aangezien er voor sommige lineaire operatoren minder dan n lineaire onafhankelijke eigenvectoren kunnen zijn. Als de matrix echter symmetrisch is, komt de wortel van de karakteristieke vergelijking van veelheid m overeen met precies m lineair onafhankelijke vectoren.

Definitie. Een symmetrische matrix is ​​een vierkante matrix waarin de elementen die symmetrisch zijn rond de hoofddiagonaal gelijk zijn, dat wil zeggen waarin .
Opmerkingen. 1. Alle eigenwaarden van een symmetrische matrix zijn reëel.
2. De eigenvectoren van een symmetrische matrix die overeenkomen met paarsgewijs verschillende eigenwaarden zijn orthogonaal.
Als een van de vele toepassingen van het bestudeerde apparaat beschouwen we het probleem van het bepalen van het type tweede-orde curve.

Eigenwaarden (getallen) en eigenvectoren.
Voorbeelden van oplossingen

Blijf jezelf

Uit beide vergelijkingen volgt dat .

Laten we het dan stellen: .

Als gevolg: – tweede eigenvector.

Laten we de belangrijke punten van het besluit herhalen:

– het resulterende systeem heeft zeker een algemene oplossing (de vergelijkingen zijn lineair afhankelijk);

– we selecteren de “y” zo dat deze een geheel getal is en de eerste “x”-coördinaat een geheel getal, positief en zo klein mogelijk is.

– we controleren of de specifieke oplossing aan elke vergelijking van het systeem voldoet.

Antwoord .

Er waren voldoende tussenliggende ‘controlepunten’, dus het controleren van de gelijkheid is in principe niet nodig.

In verschillende informatiebronnen worden de coördinaten van eigenvectoren vaak niet in kolommen, maar in rijen geschreven, bijvoorbeeld: (en eerlijk gezegd ben ik er zelf aan gewend om ze in regels op te schrijven). Deze optie is acceptabel, maar in het licht van het onderwerp lineaire transformaties technisch handiger in gebruik kolom vectoren.

Misschien leek de oplossing je erg lang, maar dat komt alleen omdat ik het eerste voorbeeld gedetailleerd heb becommentarieerd.

Voorbeeld 2

Matrices

Laten we zelf trainen! Een benaderend voorbeeld van een eindtaak aan het einde van de les.

Soms moet u een extra taak uitvoeren, namelijk:

schrijf de canonieke matrixontbinding

Wat het is?

Als de eigenvectoren van de matrix vormen basis, dan kan het worden weergegeven als:

Waar is een matrix samengesteld uit coördinaten van eigenvectoren, – diagonaal matrix met bijbehorende eigenwaarden.

Deze matrixontleding wordt genoemd canoniek of diagonaal.

Laten we eens kijken naar de matrix van het eerste voorbeeld. Zijn eigenvectoren lineair onafhankelijk(niet-collineair) en vormen een basis. Laten we een matrix van hun coördinaten maken:

Op hoofddiagonaal matrices in de juiste volgorde de eigenwaarden bevinden zich en de overige elementen zijn gelijk aan nul:
– Ik benadruk nogmaals het belang van orde: “twee” komt overeen met de 1e vector en bevindt zich daarom in de 1e kolom, “drie” – met de 2e vector.

Gebruik het gebruikelijke algoritme voor het vinden omgekeerde matrix of Gauss-Jordan-methode we vinden . Nee, dat is geen typfout! - vóór jou is een zeldzame gebeurtenis, zoals een zonsverduistering, waarbij het omgekeerde samenviel met de oorspronkelijke matrix.

Rest ons nog de canonieke ontbinding van de matrix op te schrijven:

Het systeem kan worden opgelost met behulp van elementaire transformaties, en in de volgende voorbeelden zullen we onze toevlucht nemen tot deze methode. Maar hier werkt de “school”-methode veel sneller. Uit de derde vergelijking drukken we het volgende uit: – substitueren in de tweede vergelijking:

Omdat de eerste coördinaat nul is, verkrijgen we een systeem, uit elke vergelijking waarvan volgt dat .

En opnieuw let op de verplichte aanwezigheid van een lineaire relatie. Als er maar een triviale oplossing wordt verkregen , dan is ofwel de eigenwaarde onjuist gevonden, ofwel is het systeem met een fout gecompileerd/opgelost.

Compacte coördinaten geven de waarde

Eigenvector:

En nogmaals controleren we of de oplossing is gevonden voldoet aan elke vergelijking van het systeem. In de volgende paragrafen en in de daaropvolgende taken raad ik aan om deze wens als een verplichte regel te beschouwen.

2) Voor de eigenwaarde verkrijgen we, volgens hetzelfde principe, het volgende systeem:

Uit de tweede vergelijking van het systeem drukken we het volgende uit: – substitueren in de derde vergelijking:

Omdat de “zeta”-coördinaat gelijk is aan nul, verkrijgen we uit elke vergelijking een systeem waaruit een lineaire afhankelijkheid volgt.

Laten

Controleren of dit de oplossing is voldoet aan elke vergelijking van het systeem.

De eigenvector is dus: .

3) En tenslotte komt het systeem overeen met de eigenwaarde:

De tweede vergelijking ziet er het eenvoudigst uit, dus laten we deze uitdrukken en vervangen door de eerste en derde vergelijking:

Alles is in orde - er is een lineaire relatie ontstaan, die we vervangen door de uitdrukking:

Als resultaat werden “x” en “y” uitgedrukt via “z”: . In de praktijk is het niet nodig om precies zulke relaties te bereiken; in sommige gevallen is het handiger om zowel through or als through uit te drukken. Of zelfs 'trainen' - bijvoorbeeld 'X' tot 'I' en 'I' tot 'Z'

Laten we het dan stellen:

Wij controleren of de oplossing gevonden is voldoet aan elke vergelijking van het systeem en schrijft de derde eigenvector

Antwoord: eigenvectoren:

Geometrisch definiëren deze vectoren drie verschillende ruimtelijke richtingen ("Heen en weer"), volgens welke lineaire transformatie transformeert niet-nul vectoren (eigenvectoren) in collineaire vectoren.

Als de voorwaarde het vinden van de canonieke ontbinding vereist, dan is dit hier mogelijk, omdat verschillende eigenwaarden komen overeen met verschillende lineair onafhankelijke eigenvectoren. Een matrix maken van hun coördinaten, een diagonale matrix van relevant eigenwaarden en vinden omgekeerde matrix .

Als u, onder voorwaarde, moet schrijven lineaire transformatiematrix in de basis van eigenvectoren, dan geven we het antwoord in het formulier . Er is een verschil, en het verschil is aanzienlijk! Omdat deze matrix de “de” matrix is.

Een probleem met eenvoudigere berekeningen die u zelf kunt oplossen:

Voorbeeld 5

Vind eigenvectoren van een lineaire transformatie gegeven door een matrix

Probeer bij het vinden van uw eigen getallen niet helemaal naar een polynoom van de derde graad te gaan. Bovendien kunnen uw systeemoplossingen verschillen van mijn oplossingen – hier bestaat geen zekerheid; en de vectoren die u vindt, kunnen verschillen van de voorbeeldvectoren, afhankelijk van de evenredigheid van hun respectievelijke coördinaten. Bijvoorbeeld, en. Het is esthetisch aantrekkelijker om het antwoord in de vorm te presenteren, maar het is prima als je stopt bij de tweede optie. Er zijn echter aan alles redelijke grenzen; de versie ziet er niet meer zo goed uit.

Een benaderend eindvoorbeeld van de opdracht aan het einde van de les.

Hoe los je het probleem op bij meerdere eigenwaarden?

Het algemene algoritme blijft hetzelfde, maar heeft zijn eigen kenmerken, en het is raadzaam om sommige delen van de oplossing in een striktere academische stijl te houden:

Voorbeeld 6

Vind eigenwaarden en eigenvectoren

Oplossing

Laten we natuurlijk de fantastische eerste kolom met een hoofdletter schrijven:

En, na het ontbinden van de kwadratische trinominaal:

Als resultaat worden eigenwaarden verkregen, waarvan er twee veelvouden zijn.

Laten we de eigenvectoren vinden:

1) Laten we een eenzame soldaat behandelen volgens een “vereenvoudigd” schema:

Uit de laatste twee vergelijkingen is de gelijkheid duidelijk zichtbaar, die uiteraard moet worden vervangen door de eerste vergelijking van het systeem:

Een betere combinatie vind je niet:
Eigenvector:

2-3) Nu verwijderen we een paar schildwachten. In dit geval kan het blijken twee of één eigenvector. Ongeacht de veelheid van de wortels vervangen we de waarde door de determinant wat ons het volgende brengt homogeen systeem van lineaire vergelijkingen:

Eigenvectoren zijn precies vectoren
fundamenteel systeem van oplossingen

Eigenlijk hebben we de hele les niets anders gedaan dan de vectoren van het fundamentele systeem vinden. Alleen was deze term voorlopig niet bijzonder vereist. Trouwens, die slimme studenten die het onderwerp in camouflagepakken hebben gemist homogene vergelijkingen, zal het nu moeten roken.

De enige actie was het verwijderen van de extra lijnen. Het resultaat is een matrix van één bij drie met een formele ‘stap’ in het midden.
– basisvariabele, – vrije variabelen. Er zijn dus twee vrije variabelen er zijn ook twee vectoren van het fundamentele systeem.

Laten we de basisvariabele uitdrukken in termen van vrije variabelen: . Dankzij de nulvermenigvuldiger voor de "X" kan hij absoluut alle waarden aannemen (wat duidelijk zichtbaar is in het systeem van vergelijkingen).

In de context van dit probleem is het handiger om de algemene oplossing niet in een rij, maar in een kolom te schrijven:

Het paar komt overeen met een eigenvector:
Het paar komt overeen met een eigenvector:

Opmerking : geavanceerde lezers kunnen deze vectoren mondeling selecteren - eenvoudigweg door het systeem te analyseren , maar hier is enige kennis nodig: er zijn drie variabelen, systeemmatrix rang- één, wat betekent fundamenteel beslissingssysteem bestaat uit 3 – 1 = 2 vectoren. De gevonden vectoren zijn echter ook zonder deze kennis duidelijk zichtbaar, puur op intuïtief niveau. In dit geval wordt de derde vector nog “mooier” geschreven: . Ik waarschuw u echter dat in een ander voorbeeld een eenvoudige selectie misschien niet mogelijk is, en daarom is de clausule bedoeld voor ervaren mensen. Waarom nemen we bovendien niet bijvoorbeeld de derde vector? De coördinaten ervan voldoen immers ook aan elke vergelijking van het systeem en aan de vectoren lineair onafhankelijk. Deze optie is in principe geschikt, maar "scheef", aangezien de "andere" vector een lineaire combinatie is van vectoren van het fundamentele systeem.

Antwoord: eigenwaarden: , eigenvectoren:

Een soortgelijk voorbeeld voor een onafhankelijke oplossing:

Voorbeeld 7

Vind eigenwaarden en eigenvectoren

Een voorbeeld van het uiteindelijke ontwerp bij benadering aan het einde van de les.

Opgemerkt moet worden dat in zowel het 6e als het 7e voorbeeld een drietal lineair onafhankelijke eigenvectoren wordt verkregen, en daarom is de oorspronkelijke matrix representatief in de canonieke ontbinding. Maar dergelijke frambozen komen niet in alle gevallen voor:

Voorbeeld 8

Oplossing: Laten we de karakteristieke vergelijking maken en oplossen:

Laten we de determinant in de eerste kolom uitbreiden:

We voeren verdere vereenvoudigingen uit volgens de beschouwde methode, waarbij we de derdegraadspolynoom vermijden:

– eigenwaarden.

Laten we de eigenvectoren vinden:

1) Er zijn geen problemen met de wortel:

Wees niet verrast: naast de kit zijn er ook variabelen in gebruik - er is hier geen verschil.

Vanuit de derde vergelijking drukken we het uit en vervangen we het door de eerste en tweede vergelijking:

Uit beide vergelijkingen volgt:

Laat dan:

2-3) Voor meerdere waarden krijgen we het systeem .

Laten we de matrix van het systeem opschrijven en deze, met behulp van elementaire transformaties, in een stapsgewijze vorm brengen:

www.site maakt het mogelijk om te vinden. De site voert de berekening uit. Binnen een paar seconden geeft de server de juiste oplossing. De karakteristieke vergelijking voor de matrix zal een algebraïsche uitdrukking zijn die wordt gevonden met behulp van de regel voor het berekenen van de determinant matrices matrices, terwijl er langs de hoofddiagonaal verschillen zullen zijn in de waarden van de diagonale elementen en de variabele. Bij het berekenen karakteristieke vergelijking voor de matrix online, elk element matrices zal worden vermenigvuldigd met overeenkomstige andere elementen matrices. Zoek in modus online alleen mogelijk voor vierkant matrices. Operatie zoeken karakteristieke vergelijking voor de matrix online reduceert tot het berekenen van de algebraïsche som van het product van elementen matrices als resultaat van het vinden van de determinant matrices, uitsluitend ter bepaling karakteristieke vergelijking voor de matrix online. Deze operatie neemt in de theorie een bijzondere plaats in matrices, kunt u eigenwaarden en vectoren vinden met behulp van wortels. De taak van het vinden karakteristieke vergelijking voor de matrix online bestaat uit vermenigvuldigende elementen matrices gevolgd door het optellen van deze producten volgens een bepaalde regel. www.site vondsten karakteristieke vergelijking voor de matrix gegeven dimensie in modus online. Berekening karakteristieke vergelijking voor de matrix online gezien zijn dimensie is dit het vinden van een polynoom met numerieke of symbolische coëfficiënten, gevonden volgens de regel voor het berekenen van de determinant matrices- als de som van de producten van de overeenkomstige elementen matrices, uitsluitend ter bepaling karakteristieke vergelijking voor de matrix online. Een polynoom vinden met betrekking tot een variabele voor een kwadratisch matrices, als definitie karakteristieke vergelijking voor de matrix, gebruikelijk in theorie matrices. De betekenis van de wortels van een polynoom karakteristieke vergelijking voor de matrix online gebruikt om eigenvectoren en eigenwaarden voor te bepalen matrices. Bovendien, als de determinant matrices zal dan gelijk zijn aan nul karakteristieke vergelijking van de matrix zal nog steeds bestaan, in tegenstelling tot het omgekeerde matrices. Om te berekenen karakteristieke vergelijking voor de matrix of zoek er meerdere tegelijk matrices karakteristieke vergelijkingen, moet u veel tijd en moeite besteden, terwijl onze server het binnen enkele seconden zal vinden karakteristieke vergelijking voor matrix online. In dit geval het antwoord op het vinden karakteristieke vergelijking voor de matrix online zal correct en met voldoende nauwkeurigheid zijn, zelfs als de cijfers bij het vinden zijn karakteristieke vergelijking voor de matrix online zal irrationeel zijn. Op de site www.site Tekeninvoer is toegestaan ​​in elementen matrices, dat is karakteristieke vergelijking voor matrix online kan bij de berekening in algemene symbolische vorm worden weergegeven karakteristieke vergelijking van de matrix online. Het is handig om het verkregen antwoord te controleren bij het oplossen van het probleem van het vinden karakteristieke vergelijking voor de matrix online gebruik van de site www.site. Bij het uitvoeren van de bewerking voor het berekenen van een polynoom - karakteristieke vergelijking van de matrix, moet u voorzichtig en uiterst gefocust zijn bij het oplossen van dit probleem. Onze site zal u op zijn beurt helpen uw beslissing over het onderwerp te controleren karakteristieke vergelijking van een matrix online. Als je geen tijd hebt voor lange controles van opgeloste problemen, dan www.site zal zeker een handig hulpmiddel zijn om te controleren bij het vinden en berekenen karakteristieke vergelijking voor de matrix online.

Een eigenvector van een vierkante matrix is ​​er een die, vermenigvuldigd met een gegeven matrix, resulteert in een collineaire vector. In eenvoudige woorden: wanneer een matrix wordt vermenigvuldigd met een eigenvector, blijft deze hetzelfde, maar vermenigvuldigd met een bepaald getal.

Definitie

Een eigenvector is een vector V die niet nul is en die, wanneer deze wordt vermenigvuldigd met een vierkante matrix M, zelf wordt verhoogd met een getal λ. In algebraïsche notatie ziet het er als volgt uit:

M × V = λ × V,

waarbij λ de eigenwaarde van de matrix M is.

Laten we een numeriek voorbeeld bekijken. Om de registratie te vergemakkelijken, worden de getallen in de matrix gescheiden door een puntkomma. Laten we een matrix maken:

• M = 0; 4;
• 6; 10.

Laten we het vermenigvuldigen met een kolomvector:

• V = -2;

Wanneer we een matrix vermenigvuldigen met een kolomvector, krijgen we ook een kolomvector. In strikte wiskundige taal zal de formule voor het vermenigvuldigen van een 2 × 2-matrix met een kolomvector er als volgt uitzien:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 betekent het element van matrix M dat zich in de eerste rij en eerste kolom bevindt, en M22 betekent het element dat zich in de tweede rij en tweede kolom bevindt. Voor onze matrix zijn deze elementen gelijk aan M11 = 0, M12 = 4, M21 = 6, M22 10. Voor een kolomvector zijn deze waarden gelijk aan V11 = –2, V21 = 1. Volgens deze formule, we krijgen het volgende resultaat van het product van een vierkante matrix door een vector:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Laten we voor het gemak de kolomvector in een rij schrijven. We hebben dus de vierkante matrix vermenigvuldigd met de vector (-2; 1), wat resulteerde in de vector (4; -2). Het is duidelijk dat dit dezelfde vector is, vermenigvuldigd met λ = -2. Lambda geeft in dit geval de eigenwaarde van de matrix aan.

Een eigenvector van een matrix is ​​een collineaire vector, dat wil zeggen een object dat zijn positie in de ruimte niet verandert wanneer het wordt vermenigvuldigd met een matrix. Het concept van collineariteit in vectoralgebra is vergelijkbaar met de term van parallellisme in de meetkunde. In een geometrische interpretatie zijn collineaire vectoren parallel gerichte segmenten met verschillende lengtes. Sinds de tijd van Euclides weten we dat één lijn een oneindig aantal lijnen evenwijdig heeft, dus het is logisch om aan te nemen dat elke matrix een oneindig aantal eigenvectoren heeft.

Uit het vorige voorbeeld is het duidelijk dat eigenvectoren (-8; 4), en (16; -8) en (32, -16) kunnen zijn. Dit zijn allemaal collineaire vectoren die overeenkomen met de eigenwaarde λ = -2. Wanneer we de oorspronkelijke matrix met deze vectoren vermenigvuldigen, krijgen we nog steeds een vector die 2 keer verschilt van het origineel. Dat is de reden waarom het bij het oplossen van problemen bij het vinden van een eigenvector noodzakelijk is om alleen lineair onafhankelijke vectorobjecten te vinden. Meestal zijn er voor een n × n matrix een n aantal eigenvectoren. Onze rekenmachine is ontworpen voor de analyse van vierkante matrices van de tweede orde, dus het resultaat zal bijna altijd twee eigenvectoren opleveren, behalve in gevallen waarin ze samenvallen.

In het bovenstaande voorbeeld kenden we de eigenvector van de oorspronkelijke matrix van tevoren en bepaalden we duidelijk het lambdagetal. In de praktijk gebeurt alles echter andersom: eerst worden de eigenwaarden gevonden en pas daarna de eigenvectoren.

Oplossingsalgoritme

Laten we opnieuw naar de oorspronkelijke matrix M kijken en proberen beide eigenvectoren te vinden. De matrix ziet er dus als volgt uit:

• M = 0; 4;
• 6; 10.

Eerst moeten we de eigenwaarde λ bepalen, waarvoor we de determinant van de volgende matrix moeten berekenen:

• (0 − λ); 4;
• 6; (10 − λ).

Deze matrix wordt verkregen door de onbekende λ af te trekken van de elementen op de hoofddiagonaal. De determinant wordt bepaald met behulp van de standaardformule:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Omdat onze vector niet nul moet zijn, accepteren we de resulterende vergelijking als lineair afhankelijk en stellen we onze determinant detA gelijk aan nul.

(0 − λ) × (10 − λ) − 24 = 0

Laten we de haakjes openen en de karakteristieke vergelijking van de matrix verkrijgen:

λ 2 − 10λ − 24 = 0

Dit is een standaard kwadratische vergelijking die moet worden opgelost met behulp van een discriminant.

D = b2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

De wortel van de discriminant is sqrt(D) = 14, dus λ1 = -2, λ2 = 12. Nu moeten we voor elke lambda-waarde de eigenvector vinden. Laten we de systeemcoëfficiënten uitdrukken voor λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

In deze formule is E de identiteitsmatrix. Op basis van de resulterende matrix creëren we een systeem van lineaire vergelijkingen:

2x + 4j = 6x + 12j,

waarbij x en y de eigenvectorelementen zijn.

Laten we alle X's aan de linkerkant en alle Y's aan de rechterkant verzamelen. Uiteraard - 4x = 8y. Deel de uitdrukking door -4 en krijg x = –2y. Nu kunnen we de eerste eigenvector van de matrix bepalen, waarbij we alle waarden van de onbekenden nemen (denk aan de oneindigheid van lineair afhankelijke eigenvectoren). Laten we nemen y = 1, dan x = –2. Daarom ziet de eerste eigenvector eruit als V1 = (–2; 1). Keer terug naar het begin van het artikel. Met dit vectorobject hebben we de matrix vermenigvuldigd om het concept van een eigenvector te demonstreren.

Laten we nu de eigenvector voor λ = 12 vinden.

• M - λ × E = -12; 4
• 6; -2.

Laten we hetzelfde systeem van lineaire vergelijkingen maken;

• -12x + 4j = 6x − 2j
• -18x = -6j
• 3x = j.

Nu nemen we x = 1, dus y = 3. De tweede eigenvector ziet er dus uit als V2 = (1; 3). Wanneer de oorspronkelijke matrix met een gegeven vector wordt vermenigvuldigd, zal het resultaat altijd dezelfde vector zijn, vermenigvuldigd met 12. Dit is waar het oplossingsalgoritme eindigt. Nu weet je hoe je de eigenvector van een matrix handmatig kunt bepalen.

• bepalend;
• traceer, dat wil zeggen de som van de elementen op de hoofddiagonaal;
• rang, dat wil zeggen het maximale aantal lineair onafhankelijke rijen/kolommen.

Het programma werkt volgens het bovenstaande algoritme, waardoor het oplossingsproces zoveel mogelijk wordt verkort. Het is belangrijk erop te wijzen dat lambda in het programma wordt aangeduid met de letter “c”. Laten we een numeriek voorbeeld bekijken.

Voorbeeld van hoe het programma werkt

Laten we proberen de eigenvectoren voor de volgende matrix te bepalen:

• M = 5; 13;
• 4; 14.

Laten we deze waarden in de cellen van de rekenmachine invoeren en het antwoord in de volgende vorm krijgen:

• Matrixrang: 2;
• Matrixdeterminant: 18;
• Matrixtracering: 19;
• Berekening van de eigenvector: c 2 − 19.00c + 18.00 (karakteristieke vergelijking);
• Eigenvectorberekening: 18 (eerste lambdawaarde);
• Eigenvectorberekening: 1 (tweede lambdawaarde);
• Stelsel vergelijkingen voor vector 1: -13x1 + 13y1 = 4x1 − 4y1;
• Stelsel vergelijkingen voor vector 2: 4x1 + 13y1 = 4x1 + 13y1;
• Eigenvector 1: (1; 1);
• Eigenvector 2: (-3,25; 1).

We hebben dus twee lineair onafhankelijke eigenvectoren verkregen.

Conclusie

Lineaire algebra en analytische meetkunde zijn standaardvakken voor elke eerstejaars-ingenieur. Het grote aantal vectoren en matrices is angstaanjagend, en het is gemakkelijk om fouten te maken in zulke omslachtige berekeningen. Met ons programma kunnen studenten hun berekeningen controleren of automatisch het probleem van het vinden van een eigenvector oplossen. Er zijn nog andere lineaire algebra-rekenmachines in onze catalogus; gebruik ze bij uw studie of werk.

"Het eerste deel bevat de bepalingen die minimaal noodzakelijk zijn voor het begrijpen van chemometrie, en het tweede deel bevat de feiten die u moet weten voor een dieper begrip van de methoden van multivariate analyse. De presentatie wordt geïllustreerd met voorbeelden uit het Excel-werkboek Matrix.xls, dat bij dit document hoort.

Koppelingen naar voorbeelden worden als Excel-objecten in de tekst geplaatst. Deze voorbeelden zijn van abstracte aard; ze houden op geen enkele wijze verband met de problemen van de analytische chemie. Voorbeelden uit de praktijk van het gebruik van matrixalgebra in de chemometrie worden besproken in andere teksten die een verscheidenheid aan chemometrische toepassingen bestrijken.

De meeste metingen in de analytische chemie zijn niet direct, maar indirect. Dit betekent dat in het experiment in plaats van de waarde van de gewenste analyt C (concentratie) een andere waarde wordt verkregen X(signaal), gerelateerd maar niet gelijk aan C, d.w.z. X(C) ≠ C. In de regel het type afhankelijkheid X(C) is onbekend, maar gelukkig zijn de meeste metingen in de analytische chemie proportioneel. Dit betekent dat bij toenemende concentratie van C in A keer zal signaal X met dezelfde hoeveelheid toenemen, d.w.z. X(A C) = een x(C). Bovendien zijn de signalen ook additief, zodat het signaal van een monster waarin twee stoffen met de concentraties C1 en C2 aanwezig zijn gelijk zal zijn aan de som van de signalen van elke component, d.w.z. X(C1 + C2) = X(C1)+ X(C2). Proportionaliteit en additiviteit geven samen lineariteit. Er kunnen veel voorbeelden worden gegeven om het principe van lineariteit te illustreren, maar het is voldoende om de twee meest opvallende voorbeelden te noemen: chromatografie en spectroscopie. Het tweede kenmerk dat inherent is aan een experiment in de analytische chemie is meerkanaals. Moderne analytische apparatuur meet tegelijkertijd signalen voor veel kanalen. De intensiteit van de lichttransmissie wordt bijvoorbeeld voor meerdere golflengten tegelijk gemeten, d.w.z. bereik. Daarom hebben we in het experiment te maken met veel signalen X 1 , X 2 ,...., X n, karakteriserend de reeks concentraties C 1 , C 2 , ..., C m van stoffen die aanwezig zijn in het onderzochte systeem.

Rijst. 1 Spectra

Een analytisch experiment wordt dus gekenmerkt door lineariteit en multidimensionaliteit. Daarom is het handig om experimentele gegevens als vectoren en matrices te beschouwen en deze te manipuleren met behulp van de apparatuur van matrixalgebra. De vruchtbaarheid van deze aanpak wordt geïllustreerd door het getoonde voorbeeld, dat drie spectra presenteert die zijn genomen bij 200 golflengten van 4000 tot 4796 cm −1. Eerst ( X 1) en tweede ( X 2) de spectra zijn verkregen voor standaardmonsters waarin de concentraties van twee stoffen A en B bekend zijn: in het eerste monster [A] = 0,5, [B] = 0,1, en in het tweede monster [A] = 0,2, [ B] = 0,6. Wat kan er gezegd worden over een nieuw, onbekend monster, waarvan het spectrum is aangegeven X 3 ?

Laten we drie experimentele spectra bekijken X 1 , X 2 en X 3 als drie vectoren met dimensie 200. Met behulp van lineaire algebra kan men dat gemakkelijk aantonen X 3 = 0.1 X 1 +0.3 X 2, dus het derde monster bevat uiteraard alleen stoffen A en B in concentraties [A] = 0,5×0,1 + 0,2×0,3 = 0,11 en [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Basisinformatie

1.1 Matrices

Matrix bijvoorbeeld een rechthoekige getallentabel genoemd

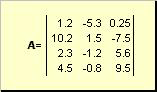
Rijst. 2 Matrix

Matrices worden aangegeven met vetgedrukte hoofdletters ( A), en hun elementen - door overeenkomstige kleine letters met indices, d.w.z. A ij. De eerste index nummert de rijen en de tweede de kolommen. In de chemometrie is het gebruikelijk om de maximale waarde van een index aan te duiden met dezelfde letter als de index zelf, maar dan in hoofdletters. Daarom de matrix A kan ook worden geschreven als ( A ij , i = 1,..., I; J = 1,..., J). Voor de voorbeeldmatrix I = 4, J= 3 en A 23 = −7.5.

Paar cijfers I En J wordt de dimensie van de matrix genoemd en wordt aangegeven als I× J. Een voorbeeld van een matrix in de chemometrie is een reeks spectra die zijn verkregen I monsters voor J golflengten.

1.2. De eenvoudigste bewerkingen met matrices

Matrixen kunnen dat zijn vermenigvuldigen met getallen. In dit geval wordt elk element vermenigvuldigd met dit getal. Bijvoorbeeld -

Rijst. 3 Een matrix vermenigvuldigen met een getal

Twee matrices met dezelfde dimensie kunnen element voor element zijn vouw En aftrekken. Bijvoorbeeld,

Rijst. 4 Matrixoptelling

Als resultaat van vermenigvuldiging met een getal en optelling wordt een matrix van dezelfde dimensie verkregen.

Een nulmatrix is ​​een matrix bestaande uit nullen. Het is aangewezen O. Dat is duidelijk A+O = A, A−A = O en 0 A = O.

De matrix kan zijn transponeren. Tijdens deze operatie wordt de matrix omgedraaid, d.w.z. rijen en kolommen worden verwisseld. Transpositie wordt aangegeven door een priemgetal, A" of indexeren A T. Dus als A = {A ij , i = 1,..., I; J = 1,...,J), Dat A t = ( A ji , J = 1,...,J; ik = 1,..., I). Bijvoorbeeld

Rijst. 5 Matrixtranspositie

Het is duidelijk dat ( A t) t = A, (A+B)T =EEN t+ B T.

1.3. Matrix vermenigvuldiging

Matrixen kunnen dat zijn vermenigvuldigen, maar alleen als ze de juiste afmetingen hebben. Waarom dit zo is, zal duidelijk worden uit de definitie. Matrixproduct A, afmeting I× K en matrices B, afmeting K× J, wordt een matrix genoemd C, afmeting I× J, waarvan de elementen getallen zijn

Dus voor het product AB het is noodzakelijk dat het aantal kolommen in de linkermatrix A was gelijk aan het aantal rijen in de rechtermatrix B. Een voorbeeld van een matrixproduct -

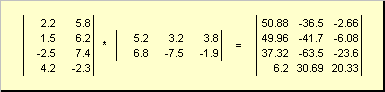
Fig.6 Product van matrices

De regel voor matrixvermenigvuldiging kan als volgt worden geformuleerd. Een matrixelement vinden C, staande op de kruising i-de lijn en J e kolom ( C ij) moet element voor element worden vermenigvuldigd i-de rij van de eerste matrix A op J e kolom van de tweede matrix B en tel alle resultaten bij elkaar op. Dus in het getoonde voorbeeld wordt een element uit de derde rij en de tweede kolom verkregen als de som van de elementaire producten van de derde rij A en tweede kolom B

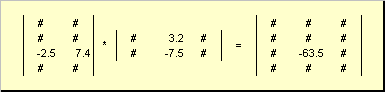
Fig.7 Element van het product van matrices

Het product van matrices hangt af van de volgorde, d.w.z. AB ≠ B.A., althans om dimensionele redenen. Ze zeggen dat het niet-commutatief is. Het product van matrices is echter associatief. Het betekent dat abc = (AB)C = A(BC). Bovendien is het ook distributief, d.w.z. A(B+C) = AB+A.C.. Dat is duidelijk AO = O.

1.4. Vierkante matrices

Als het aantal matrixkolommen gelijk is aan het aantal rijen ( I = J=N), dan wordt zo’n matrix vierkant genoemd. In deze sectie zullen we alleen dergelijke matrices beschouwen. Onder deze matrices kunnen matrices met bijzondere eigenschappen worden onderscheiden.

Enkel matrix (aangeduid I, en soms E) is een matrix waarin alle elementen gelijk zijn aan nul, met uitzondering van diagonale elementen, die gelijk zijn aan 1, d.w.z.

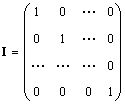
Blijkbaar AI = IA. = A.

De matrix wordt genoemd diagonaal, als al zijn elementen behalve diagonale ( A ii) zijn gelijk aan nul. Bijvoorbeeld

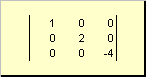
Rijst. 8 Diagonale matrix

Matrix A de top genoemd driehoekig, als alle elementen die onder de diagonaal liggen gelijk zijn aan nul, d.w.z. A ij= 0, op i>J. Bijvoorbeeld

Rijst. 9 Bovenste driehoekige matrix

De onderste driehoekige matrix wordt op dezelfde manier gedefinieerd.

Matrix A genaamd symmetrisch, Als A t = A. Met andere woorden A ij = A ji. Bijvoorbeeld

Rijst. 10 Symmetrische matrix

Matrix A genaamd orthogonaal, Als

A T A = AA t = I.

De matrix wordt genoemd normaal Als

1.5. Spoor en bepalend

Volgende vierkante matrix A(aangegeven met Tr( A) of Sp( A)) is de som van de diagonale elementen,

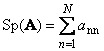
Bijvoorbeeld,

Rijst. 11 Matrixtracering

Dat is duidelijk

Sp(α A) = αSp( A) En

Sp( A+B) = Sp( A)+Sp( B).

Dat kan worden aangetoond

Sp( A) = Sp( A t), Sp( I) = N,

en ook dat

Sp( AB) = Sp( B.A.).

Een ander belangrijk kenmerk van een vierkante matrix is ​​zijn bepalend(aangeduid det( A)). Het bepalen van de determinant in het algemene geval is behoorlijk moeilijk, dus we zullen beginnen met de eenvoudigste optie: de matrix A afmeting (2×2). Dan

Voor een (3×3) matrix zal de determinant gelijk zijn aan

In het geval van de matrix ( N× N) wordt de determinant berekend als de som 1·2·3· ... · N= N! termen, die allemaal gelijk zijn

Indexen k 1 , k 2 ,..., k N worden gedefinieerd als alle mogelijke geordende permutaties R getallen in de set (1, 2, ..., N). Het berekenen van de determinant van een matrix is ​​een complexe procedure, die in de praktijk wordt uitgevoerd met behulp van speciale programma's. Bijvoorbeeld,

Rijst. 12 Matrixdeterminant

Laten we alleen de voor de hand liggende eigenschappen opmerken:

det( I) = 1, det( A) = det( A T),

det( AB) = det( A)det( B).

1.6. Vectoren

Als de matrix uit slechts één kolom bestaat ( J= 1), dan wordt zo’n object aangeroepen vector. Meer precies, een kolomvector. Bijvoorbeeld

Men kan bijvoorbeeld ook denken aan matrices die uit één rij bestaan

Dit object is ook een vector, maar rij vector. Bij het analyseren van gegevens is het belangrijk om te begrijpen met welke vectoren we te maken hebben: kolommen of rijen. Het spectrum dat voor één monster wordt genomen, kan dus worden beschouwd als een rijvector. Vervolgens moet de reeks spectrale intensiteiten bij een bepaalde golflengte voor alle monsters worden behandeld als een kolomvector.

De dimensie van een vector is het aantal elementen ervan.

Het is duidelijk dat elke kolomvector door transpositie in een rijvector kan worden veranderd, d.w.z.

In gevallen waarin de vorm van de vector niet specifiek is gespecificeerd, maar eenvoudigweg wordt gezegd dat het een vector is, bedoelen ze een kolomvector. Ook wij zullen ons aan deze regel houden. Een vector wordt aangegeven met een kleine, rechtopstaande, vetgedrukte letter. Een nulvector is een vector waarvan alle elementen nul zijn. Het is aangewezen 0 .

1.7. De eenvoudigste bewerkingen met vectoren

Vectoren kunnen op dezelfde manier als matrices met getallen worden opgeteld en vermenigvuldigd. Bijvoorbeeld,

Rijst. 13 Bewerkingen met vectoren

Twee vectoren X En j worden genoemd colineair, als er een getal α bestaat zodanig dat

1.8. Producten van vectoren

Twee vectoren van dezelfde dimensie N kan worden vermenigvuldigd. Stel dat er twee vectoren zijn X = (X 1 , X 2 ,...,X N)t en j = (j 1 , j 2 ,...,j N) t. Geleid door de rij-voor-kolom-vermenigvuldigingsregel kunnen we hieruit twee producten samenstellen: X T j En xy T. Eerste werk

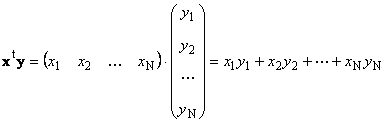
genaamd scalair of intern. Het resultaat is een getal. Het wordt ook aangegeven met ( X,j)= X T j. Bijvoorbeeld,

Rijst. 14 Inwendig (scalair) product

Tweede stuk

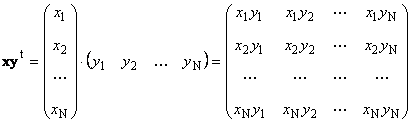
genaamd extern. Het resultaat is een matrix van dimensie ( N× N). Bijvoorbeeld,

Rijst. 15 Extern werk

Vectoren waarvan het scalaire product nul is, worden genoemd orthogonaal.

1.9. Vectornorm

Het scalaire product van een vector met zichzelf wordt een scalair vierkant genoemd. Deze waarde

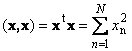
definieert een vierkant lengte vector X. Om de lengte aan te geven (ook wel de norm vector) wordt de notatie gebruikt

Bijvoorbeeld,

Rijst. 16 Vectornorm

Eenheidslengtevector (|| X|| = 1) wordt genormaliseerd genoemd. Niet-nul vector ( X ≠ 0 ) kan worden genormaliseerd door het te delen door de lengte, d.w.z. X = ||X|| (X/||X||) = ||X|| e. Hier e = X/||X|| - genormaliseerde vector.

Vectoren worden orthonormaal genoemd als ze allemaal genormaliseerd en paarsgewijze orthogonaal zijn.

1.10. Hoek tussen vectoren

Het scalaire product bepaalt en hoekφ tussen twee vectoren X En j

Als de vectoren orthogonaal zijn, dan is cosφ = 0 en φ = π/2, en als ze colineair zijn, dan is cosφ = 1 en φ = 0.

1.11. Vectorweergave van een matrix

Elke matrix A maat I× J kan worden weergegeven als een verzameling vectoren

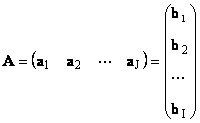
Hier elke vector A J is J e kolom en de rijvector B i is i e rij van de matrix A

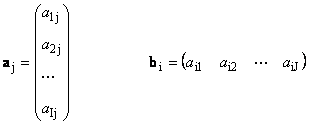
1.12. Lineair afhankelijke vectoren

Vectoren met dezelfde dimensie ( N) kan worden opgeteld en vermenigvuldigd met een getal, net als matrices. Het resultaat is een vector met dezelfde dimensie. Stel dat er meerdere vectoren zijn met dezelfde dimensie X 1 , X 2 ,...,X K en hetzelfde aantal getallen α α 1 , α 2 ,...,α K. Vector

j= α 1 X 1 + α2 X 2 +...+ α K X K

genaamd lineaire combinatie vectoren X k .

Als er zulke niet-nul getallen α zijn k ≠ 0, k = 1,..., K, Wat j = 0 , dan zo'n reeks vectoren X k genaamd lineair afhankelijk. Anders wordt gezegd dat de vectoren lineair onafhankelijk zijn. Bijvoorbeeld vectoren X 1 = (2, 2)t en X 2 = (−1, −1) t zijn lineair afhankelijk, omdat X 1 +2X 2 = 0

1.13. Matrix-rang

Overweeg een set K vectoren X 1 , X 2 ,...,X K dimensies N. De rang van dit vectorsysteem is het maximale aantal lineair onafhankelijke vectoren. Bijvoorbeeld in het setje

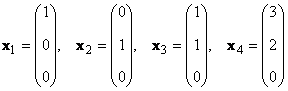
er zijn bijvoorbeeld slechts twee lineair onafhankelijke vectoren X 1 en X 2, dus de rangorde is 2.

Het is duidelijk dat als er meer vectoren in een verzameling zitten dan hun dimensie ( K>N), dan zijn ze noodzakelijkerwijs lineair afhankelijk.

Matrix-rang(aangegeven door rang( A)) is de rangorde van het vectorsysteem waaruit het bestaat. Hoewel elke matrix op twee manieren kan worden weergegeven (kolom- of rijvectoren), heeft dit geen invloed op de rangordewaarde, omdat

1.14. omgekeerde matrix

Vierkante matrix A wordt niet-gedegenereerd genoemd als het een uniek karakter heeft achteruit Matrix A-1, bepaald door de voorwaarden

AA −1 = A −1 A = I.

De inverse matrix bestaat niet voor alle matrices. Een noodzakelijke en voldoende voorwaarde voor niet-degeneratie is

det( A) ≠ 0 of rang( A) = N.

Matrixinversie is een complexe procedure waarvoor speciale programma's bestaan. Bijvoorbeeld,

Rijst. 17 Matrix-inversie

Laten we de formules presenteren voor het eenvoudigste geval: een 2×2-matrix

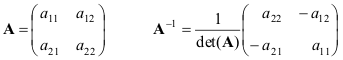
Als matrices A En B zijn dus niet-gedegenereerd

(AB) −1 = B −1 A −1 .

1.15. Pseudo-inverse matrix

Als matrix A singulier is en de inverse matrix niet bestaat, dan kunt u in sommige gevallen gebruik maken van pseudo-invers matrix, die als een dergelijke matrix is ​​gedefinieerd A+ dat

AA + A = A.

De pseudo-inverse matrix is ​​niet de enige en de vorm ervan hangt af van de constructiemethode. Voor een rechthoekige matrix kunt u bijvoorbeeld de Moore-Penrose-methode gebruiken.

Als het aantal kolommen kleiner is dan het aantal rijen, dan

A + =(A T A) −1 A T

Bijvoorbeeld,

Rijst. 17a Pseudo-inversie van een matrix

Als het aantal kolommen groter is dan het aantal rijen, dan

A + =A T ( AA T) −1

1.16. Een vector vermenigvuldigen met een matrix

Vector X kan worden vermenigvuldigd met een matrix A geschikte maat. In dit geval wordt de kolomvector rechts vermenigvuldigd Bijl en de vectorrij bevindt zich aan de linkerkant X T A. Als de vectordimensie J en de matrixdimensie I× J dan zal het resultaat een dimensievector zijn I. Bijvoorbeeld,

Rijst. 18 Een vector vermenigvuldigen met een matrix

Als matrix A- vierkant ( I× I), en vervolgens de vector j = Bijl heeft dezelfde afmeting als X. Dat is duidelijk

A(α 1 X 1 + α2 X 2) = α 1 Bijl 1 + α2 Bijl 2 .

Daarom kunnen matrices worden beschouwd als lineaire transformaties van vectoren. In het bijzonder Ix = X, Os = 0 .

2. Aanvullende informatie

2.1. Systemen van lineaire vergelijkingen

Laten A- matrixgrootte I× J, A B- dimensievector J. Overweeg de vergelijking

Bijl = B

ten opzichte van de vector X, dimensies I. In wezen is het een systeem van I lineaire vergelijkingen met J onbekend X 1 ,...,X J. Er bestaat een oplossing dan en slechts dan als

rang( A) = rang( B) = R,

Waar B is een uitgebreide matrix van dimensies I×( J+1), bestaande uit een matrix A, aangevuld met een kolom B, B = (A B). Anders zijn de vergelijkingen inconsistent.

Als R = I = J, dan is de oplossing uniek

X = A −1 B.

Als R < I, dan zijn er veel verschillende oplossingen die kunnen worden uitgedrukt door middel van een lineaire combinatie J−R vectoren. Systeem van homogene vergelijkingen Bijl = 0 met vierkante matrix A (N× N) heeft een niet-triviale oplossing ( X ≠ 0 ) dan en slechts dan als det( A) = 0. Als R= rang( A)<N, dan zijn er N−R lineair onafhankelijke oplossingen.

2.2. Bilineaire en kwadratische vormen

Als A is een vierkante matrix, en X En j- vector van de overeenkomstige dimensie, vervolgens het scalaire product van de vorm X T Ja genaamd bilineair vorm gedefinieerd door matrix A. Bij X = j uitdrukking X T Bijl genaamd kwadratisch formulier.

2.3. Positief definitieve matrices

Vierkante matrix A genaamd positief gedefineerd, indien voor elke vector die niet nul is X ≠ 0 ,

X T Bijl > 0.

Op dezelfde manier gedefinieerd negatief (X T Bijl < 0), niet-negatief (X T Bijl≥ 0) en negatief (X T Bijl≤ 0) bepaalde matrices.

2.4. Cholesky-ontbinding

Als de symmetrische matrix A positief definiet is, dan is er een unieke driehoekige matrix U met positieve elementen, waarvoor

A = U T U.

Bijvoorbeeld,

Rijst. 19 Cholesky-ontbinding

2.5. Polaire ontbinding

Laten A is een niet-singuliere vierkante dimensiematrix N× N. Dan is er sprake van een unicum polair prestatie

A = SR

Waar S is een niet-negatieve symmetrische matrix, en R is een orthogonale matrix. Matrices S En R kan expliciet worden gedefinieerd:

S 2 = AA t of S = (AA t) ½ en R = S −1 A = (AA t) −½ A.

Bijvoorbeeld,

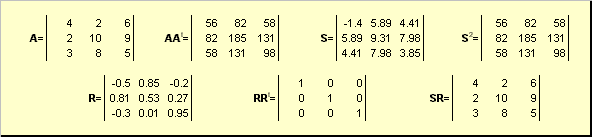
Rijst. 20 Polaire ontbinding

Als matrix A gedegenereerd is, dan is de ontbinding niet uniek - namelijk: S nog steeds alleen, maar R misschien veel. Polaire ontbinding vertegenwoordigt de matrix A als een combinatie van compressie/extensie S en draai R.

2.6. Eigenvectoren en eigenwaarden

Laten A is een vierkante matrix. Vector v genaamd eigenvector matrices A, Als

Gem = λ v,

waar het getal λ wordt genoemd eigenwaarde matrices A. Dus de transformatie die de matrix uitvoert A boven de vector v, komt neer op eenvoudig uitrekken of samendrukken met een coëfficiënt λ. De eigenvector wordt bepaald tot vermenigvuldiging met een constante α ≠ 0, d.w.z. Als v een eigenvector is, dan is α v- ook een eigenvector.

2.7. Eigenwaarden

Bij de matrix A, afmeting ( N× N) kan niet meer zijn dan N eigenwaarden. Ze voldoen karakteristieke vergelijking

det( A − λ I) = 0,

dat is een algebraïsche vergelijking N-de bestelling. In het bijzonder heeft de karakteristieke vergelijking voor een 2×2-matrix de vorm

Bijvoorbeeld,

Rijst. 21 Eigenwaarden

Set eigenwaarden λ 1 ,..., λ N matrices A genaamd spectrum A.

Het spectrum heeft verschillende eigenschappen. In het bijzonder

det( A) = λ 1 ×...×λ N,Sp( A) = λ 1 +...+λ N.

De eigenwaarden van een willekeurige matrix kunnen complexe getallen zijn, maar als de matrix symmetrisch is ( A t = A), dan zijn de eigenwaarden reëel.

2.8. Eigenvectoren

Bij de matrix A, afmeting ( N× N) kan niet meer zijn dan N eigenvectoren, die elk overeenkomen met hun eigen eigenwaarde. Om de eigenvector te bepalen v N Je moet een systeem van homogene vergelijkingen oplossen

(A − λ N I)v N = 0 .

Het heeft een niet-triviale oplossing, aangezien det( Een −λ N I) = 0.

Bijvoorbeeld,

Rijst. 22 Eigenvectoren

De eigenvectoren van een symmetrische matrix zijn orthogonaal.