Podano układ liniowych równań algebraicznych. Jak znaleźć rozwiązania ogólne i szczególne układu równań liniowych

Równania liniowe dwóch zmiennych

Uczeń ma 200 rubli na zjedzenie obiadu w szkole. Ciasto kosztuje 25 rubli, a filiżanka kawy kosztuje 10 rubli. Ile ciast i filiżanek kawy można kupić za 200 rubli?

Oznaczmy liczbę ciastek przez X i liczbę wypitych filiżanek kawy y. Następnie koszt ciastek będzie oznaczony wyrażeniem 25 X, a koszt filiżanek kawy w 10 y .

25X- cena X ciastka
10y — cena y filiżanki kawy

Całkowita kwota powinna wynosić 200 rubli. Następnie otrzymujemy równanie z dwiema zmiennymi X I y

25X+ 10y= 200

Ile pierwiastków ma to równanie?

Wszystko zależy od apetytu ucznia. Jeśli kupi 6 ciast i 5 filiżanek kawy, pierwiastkami równania będą liczby 6 i 5.

Mówi się, że para wartości 6 i 5 jest pierwiastkiem równania 25 X+ 10y= 200 . Zapisywane jako (6; 5), gdzie pierwsza liczba jest wartością zmiennej X, a drugi - wartość zmiennej y .

Liczby 6 i 5 nie są jedynymi pierwiastkami odwracającymi równanie 25 X+ 10y= 200 do tożsamości. W razie potrzeby za te same 200 rubli student może kupić 4 ciasta i 10 filiżanek kawy:

W tym przypadku pierwiastki równania 25 X+ 10y= 200 to para wartości (4; 10).

Co więcej, uczeń może w ogóle nie kupować kawy, ale kupować ciasta za całe 200 rubli. Następnie pierwiastki równania 25 X+ 10y= 200 będzie wartością 8 i 0

Lub odwrotnie, nie kupuj ciast, ale kup kawę za całe 200 rubli. Następnie pierwiastki równania 25 X+ 10y= 200 wartości będą wynosić 0 i 20

Spróbujmy wypisać wszystkie możliwe pierwiastki równania 25 X+ 10y= 200 . Umówmy się, że wartości X I y należą do zbioru liczb całkowitych. I niech te wartości będą większe lub równe zero:

X∈Z, y∈ Z;
x ≥ 0, y ≥ 0

Będzie to wygodne dla samego ucznia. Wygodniej jest kupować całe ciasta niż na przykład kilka całych ciast i połowę ciasta. Wygodniej jest też pić kawę w całych filiżankach niż np. kilka całych filiżanek i pół filiżanki.

Zauważ, że to dziwne X w żadnych okolicznościach niemożliwe jest osiągnięcie równości y. Następnie wartości X kolejne liczby będą wynosić 0, 2, 4, 6, 8. I wiedza X można łatwo ustalić y

W ten sposób otrzymaliśmy następujące pary wartości (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Pary te są rozwiązaniami lub pierwiastkami równania 25 X+ 10y= 200. Zamieniają to równanie w tożsamość.

Równanie postaci topór + by = c zwany równanie liniowe z dwiema zmiennymi. Rozwiązaniem lub pierwiastkami tego równania jest para wartości ( X; y), co czyni ją tożsamością.

Należy również zauważyć, że jeśli równanie liniowe z dwiema zmiennymi jest zapisane w postaci topór + b y = do , potem mówią, że jest to zapisane kanoniczny(normalna) forma.

Niektóre równania liniowe dwóch zmiennych można sprowadzić do postaci kanonicznej.

Na przykład równanie 2(16X+ 3y- 4) = 2(12 + 8X − y) można przywołać na myśl topór + by = c. Otwórzmy nawiasy po obu stronach tego równania i otrzymajmy 32X + 6y − 8 = 24 + 16X − 2y . Terminy zawierające niewiadome grupujemy po lewej stronie równania, a wyrazy wolne od niewiadomych po prawej. Wtedy otrzymamy 32x− 16X+ 6y+ 2y = 24 + 8 . Przedstawiamy podobne wyrazy po obu stronach, otrzymujemy równanie 16 X+ 8y= 32. Równanie to sprowadza się do postaci topór + by = c i jest kanoniczny.

Równanie 25 omówione wcześniej X+ 10y= 200 jest także równaniem liniowym z dwiema zmiennymi w postaci kanonicznej. W tym równaniu parametry A , B I C są równe odpowiednio wartościom 25, 10 i 200.

Właściwie równanie topór + by = c ma niezliczoną ilość rozwiązań. Rozwiązanie równania 25X+ 10y= 200, szukaliśmy jego pierwiastków tylko na zbiorze liczb całkowitych. W rezultacie otrzymaliśmy kilka par wartości, które zamieniły to równanie w tożsamość. Ale na zbiorze liczb wymiernych równanie 25 X+ 10y= 200 będzie miało nieskończenie wiele rozwiązań.

Aby uzyskać nowe pary wartości, należy przyjąć dowolną wartość X, następnie ekspres y. Weźmy na przykład zmienną X wartość 7. Następnie otrzymujemy równanie z jedną zmienną 25×7 + 10y= 200 w którym można wyrazić y

Pozwalać X= 15. Następnie równanie 25X+ 10y= 200 staje się 25 × 15 + 10y= 200. Stąd to znajdujemy y = −17,5

Pozwalać X= −3 . Następnie równanie 25X+ 10y= 200 staje się 25 × (-3) + 10y= 200. Stąd to znajdujemy y = −27,5

Układ dwóch równań liniowych z dwiema zmiennymi

Dla równania topór + by = c możesz przyjmować dowolne wartości tyle razy, ile chcesz X i znajdź wartości dla y. Wzięte osobno, takie równanie będzie miało niezliczoną ilość rozwiązań.

Ale zdarza się również, że zmienne X I y połączone nie jednym, ale dwoma równaniami. W tym przypadku tworzą one tzw układ równań liniowych na dwie zmienne. Taki układ równań może mieć jedną parę wartości (czyli inaczej: „jedno rozwiązanie”).

Może się również zdarzyć, że system nie będzie miał żadnych rozwiązań. Układ równań liniowych może mieć niezliczoną ilość rozwiązań w rzadkich i wyjątkowych przypadkach.

Dwa równania liniowe tworzą układ, gdy wartości X I y wprowadź do każdego z tych równań.

Wróćmy do pierwszego równania 25 X+ 10y= 200 . Jedną z par wartości tego równania była para (6; 5). To przypadek, gdy za 200 rubli można było kupić 6 ciast i 5 filiżanek kawy.

Sformułujmy problem tak, aby para (6; 5) stała się jedynym rozwiązaniem równania 25 X+ 10y= 200 . Aby to zrobić, utwórzmy kolejne równanie, które łączyłoby to samo X ciasta i y filiżanki kawy.

Podajmy treść problemu w następujący sposób:

„Student kupił kilka ciast i kilka filiżanek kawy za 200 rubli. Ciasto kosztuje 25 rubli, a filiżanka kawy kosztuje 10 rubli. Ile ciastek i filiżanek kawy kupił uczeń, jeśli wiadomo, że liczba ciastek jest o jedną jednostkę większa od liczby filiżanek kawy?

Mamy już pierwsze równanie. To jest równanie 25 X+ 10y= 200 . Utwórzmy teraz równanie warunku „liczba ciast jest o jedną jednostkę większa niż liczba filiżanek kawy” .

Liczba ciastek jest X, a liczba filiżanek kawy wynosi y. Możesz zapisać to zdanie, korzystając z równania x-y= 1. To równanie będzie oznaczać, że różnica między ciastami i kawą wynosi 1.

x = y+ 1 . To równanie oznacza, że ​​liczba ciast jest o jeden większa niż liczba filiżanek kawy. Dlatego, aby uzyskać równość, do liczby filiżanek kawy dodaje się jedną. Można to łatwo zrozumieć, jeśli zastosujemy model skal, który rozważaliśmy podczas badania najprostszych problemów:

Mamy dwa równania: 25 X+ 10y= 200 i x = y+ 1. Ponieważ wartości X I y, czyli 6 i 5 są zawarte w każdym z tych równań, wówczas razem tworzą system. Zapiszmy ten system. Jeżeli równania tworzą układ, wówczas są one otoczone znakiem układu. Symbolem systemowym jest nawias klamrowy:

Rozwiążmy ten system. Pozwoli nam to zobaczyć, jak dochodzimy do wartości 6 i 5. Istnieje wiele metod rozwiązywania takich układów. Przyjrzyjmy się najpopularniejszym z nich.

Metoda substytucyjna

Nazwa tej metody mówi sama za siebie. Jego istotą jest podstawienie jednego równania na drugie, po uprzednim wyrażeniu jednej ze zmiennych.

W naszym systemie nic nie trzeba wyrażać. W drugim równaniu X = y+ 1 zmienna X już wyrażone. Ta zmienna jest równa wyrażeniu y+ 1 . Następnie możesz zastąpić to wyrażenie pierwszym równaniem zamiast zmiennej X

Po podstawieniu wyrażenia y Zamiast tego + 1 do pierwszego równania X, otrzymujemy równanie 25(y+ 1) + 10y= 200 . Jest to równanie liniowe z jedną zmienną. Równanie to jest dość łatwe do rozwiązania:

Znaleźliśmy wartość zmiennej y. Podstawmy teraz tę wartość do jednego z równań i znajdźmy wartość X. W tym celu wygodnie jest użyć drugiego równania X = y+ 1 . Podstawmy do niego wartość y

Oznacza to, że para (6; 5) jest rozwiązaniem układu równań, zgodnie z naszym zamierzeniem. Sprawdzamy i upewniamy się, że para (6; 5) spełnia układ:

Przykład 2

Podstawmy pierwsze równanie X= 2 + y do drugiego równania 3 x− 2y= 9. W pierwszym równaniu zmienna X równe wyrażeniu 2 + y. Zamiast tego podstawmy to wyrażenie do drugiego równania X

Teraz znajdźmy wartość X. Aby to zrobić, podstawimy wartość y do pierwszego równania X= 2 + y

Oznacza to, że rozwiązaniem układu jest wartość pary (5; 3)

Przykład 3. Rozwiąż następujący układ równań metodą podstawieniową:

Tutaj, w przeciwieństwie do poprzednich przykładów, jedna ze zmiennych nie jest wyrażona wprost.

Aby zastąpić jedno równanie drugim, najpierw potrzebujesz .

Wskazane jest wyrażenie zmiennej, która ma współczynnik jeden. Zmienna ma współczynnik jeden X, co jest zawarte w pierwszym równaniu X+ 2y= 11. Wyraźmy tę zmienną.

Po wyrażeniu zmiennym X, nasz system przyjmie następującą postać:

Teraz podstawmy pierwsze równanie do drugiego i znajdźmy wartość y

Zastąpmy y X

Oznacza to, że rozwiązaniem układu jest para wartości (3; 4)

Oczywiście można także wyrazić zmienną y. To nie zmieni korzeni. Ale jeśli wyrazisz y, Rezultatem nie jest bardzo proste równanie, którego rozwiązanie zajmie więcej czasu. Będzie to wyglądać tak:

Widzimy, że w tym przykładzie wyrażamy X o wiele wygodniejsze niż wyrażanie y .

Przykład 4. Rozwiąż następujący układ równań metodą podstawieniową:

Wyraźmy to w pierwszym równaniu X. Wtedy system przyjmie postać:

y

Zastąpmy y do pierwszego równania i znajdź X. Możesz użyć oryginalnego równania 7 X+ 9y= 8, lub użyj równania, w którym wyrażona jest zmienna X. Użyjemy tego równania, ponieważ jest wygodne:

Oznacza to, że rozwiązaniem układu jest para wartości (5; −3)

Metoda dodawania

Metoda dodawania polega na dodawaniu równań zawartych w układzie wyraz po wyrazie. Dodanie to skutkuje nowym równaniem z jedną zmienną. Rozwiązanie takiego równania jest dość proste.

Rozwiążmy następujący układ równań:

Dodajmy lewą stronę pierwszego równania do lewej strony drugiego równania. I prawa strona pierwszego równania z prawą stroną drugiego równania. Otrzymujemy następującą równość:

Przyjrzyjmy się podobnym terminom:

W rezultacie otrzymaliśmy najprostsze równanie 3 X= 27, którego pierwiastek wynosi 9. Znajomość wartości X możesz znaleźć wartość y. Zastąpmy tę wartość X do drugiego równania x-y= 3 . Otrzymujemy 9 − y= 3 . Stąd y= 6 .

Oznacza to, że rozwiązaniem układu jest para wartości (9; 6)

Przykład 2

Dodajmy lewą stronę pierwszego równania do lewej strony drugiego równania. I prawa strona pierwszego równania z prawą stroną drugiego równania. W powstałej równości przedstawiamy podobne terminy:

W rezultacie otrzymaliśmy najprostsze równanie 5 X= 20, którego pierwiastek wynosi 4. Znajomość wartości X możesz znaleźć wartość y. Zastąpmy tę wartość X do pierwszego równania 2 x+y= 11. Zdobądźmy 8+ y= 11. Stąd y= 3 .

Oznacza to, że rozwiązaniem układu jest para wartości (4;3)

Proces dodawania nie jest szczegółowo opisany. Trzeba to zrobić mentalnie. Podczas dodawania oba równania należy sprowadzić do postaci kanonicznej. Swoją drogą ac + by = c .

Z rozważanych przykładów jasno wynika, że ​​głównym celem dodawania równań jest pozbycie się jednej ze zmiennych. Jednak nie zawsze możliwe jest natychmiastowe rozwiązanie układu równań metodą dodawania. Najczęściej układ najpierw doprowadza się do postaci, w której można dodawać równania zawarte w tym układzie.

Na przykład system można rozwiązać natychmiast dodając. Po dodaniu obu równań terminy y I -y znikną, ponieważ ich suma wynosi zero. W rezultacie powstaje najprostsze równanie 11 X= 22, którego pierwiastek wynosi 2. Będzie można wtedy określić y równa 5.

I układ równań Metody dodawania nie można rozwiązać natychmiast, ponieważ nie doprowadzi to do zniknięcia jednej ze zmiennych. Dodanie da równanie 8 X+ y= 28, co ma nieskończoną liczbę rozwiązań.

Jeśli obie strony równania pomnożymy lub podzielimy przez tę samą liczbę, różną od zera, otrzymamy równanie równoważne podanemu. Zasada ta obowiązuje również w przypadku układu równań liniowych z dwiema zmiennymi. Jedno z równań (lub oba równania) można pomnożyć przez dowolną liczbę. Rezultatem będzie równoważny system, którego korzenie będą pokrywać się z poprzednim.

Wróćmy do pierwszego systemu, który opisywał, ile ciast i filiżanek kawy kupił uczeń. Rozwiązaniem tego układu była para wartości (6; 5).

Pomnóżmy oba równania zawarte w tym układzie przez pewne liczby. Powiedzmy, że mnożymy pierwsze równanie przez 2, a drugie przez 3

W rezultacie otrzymaliśmy system
Rozwiązaniem tego układu jest nadal para wartości (6; 5)

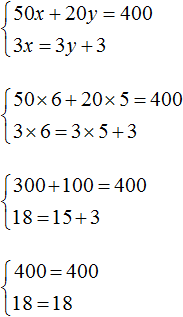
Oznacza to, że równania zawarte w układzie można sprowadzić do postaci odpowiedniej do zastosowania metody dodawania.

Wróćmy do systemu , którego nie mogliśmy rozwiązać metodą dodawania.

Pomnóż pierwsze równanie przez 6, a drugie przez -2

Otrzymujemy wtedy następujący układ:

Dodajmy równania zawarte w tym układzie. Dodawanie komponentów 12 X i -12 X spowoduje wynik 0, dodanie 18 y i 4 y dam 22 y, a dodanie 108 i -20 daje 88. Następnie otrzymujemy równanie 22 y= 88, stąd y = 4 .

Jeżeli na początku ciężko Ci w głowie dodać równania, to możesz zapisać jak lewa strona pierwszego równania sumuje się z lewą stroną drugiego równania, a prawa strona pierwszego równania z prawą stroną równania drugie równanie:

Wiedząc, że wartość zmiennej y równa się 4, możesz znaleźć wartość X. Zastąpmy y do jednego z równań, na przykład do pierwszego równania 2 X+ 3y= 18. Następnie otrzymujemy równanie z jedną zmienną 2 X+ 12 = 18. Przesuńmy 12 w prawą stronę, zmieniając znak, otrzymamy 2 X= 6, stąd X = 3 .

Przykład 4. Rozwiąż następujący układ równań metodą dodawania:

Pomnóżmy drugie równanie przez -1. Następnie system przyjmie następującą postać:

Dodajmy oba równania. Dodawanie komponentów X I −x spowoduje wynik 0, dodanie 5 y i 3 y dam 8 y, a dodanie 7 i 1 daje 8. Wynikiem jest równanie 8 y= 8, którego pierwiastek wynosi 1. Wiedząc, że wartość y równa się 1, możesz znaleźć wartość X .

Zastąpmy y do pierwszego równania, otrzymujemy X+ 5 = 7, stąd X= 2

Przykład 5. Rozwiąż następujący układ równań metodą dodawania:

Pożądane jest, aby terminy zawierające te same zmienne znajdowały się jeden pod drugim. Dlatego w drugim równaniu wyrazy 5 y i -2 X Zamieńmy się miejscami. W rezultacie system przyjmie postać:

Pomnóżmy drugie równanie przez 3. Wtedy układ przyjmie postać:

Dodajmy teraz oba równania. W wyniku dodawania otrzymujemy równanie 8 y= 16, którego pierwiastek wynosi 2.

Zastąpmy y w pierwszym równaniu otrzymujemy 6 X- 14 = 40. Przesuńmy wyraz -14 na prawą stronę, zmieniając znak i otrzymajmy 6 X= 54 . Stąd X= 9.

Przykład 6. Rozwiąż następujący układ równań metodą dodawania:

Pozbądźmy się ułamków. Pomnóż pierwsze równanie przez 36, a drugie przez 12

W powstałym układzie pierwsze równanie można pomnożyć przez -5, a drugie przez 8

Dodajmy równania w powstałym układzie. Następnie otrzymujemy najprostsze równanie -13 y= −156 . Stąd y= 12. Zastąpmy y do pierwszego równania i znajdź X

Przykład 7. Rozwiąż następujący układ równań metodą dodawania:

Sprowadźmy oba równania do postaci normalnej. Tutaj wygodnie jest zastosować zasadę proporcji w obu równaniach. Jeżeli w pierwszym równaniu prawa strona jest przedstawiona jako , a prawa strona drugiego równania jako , to układ będzie miał postać:

Mamy proporcję. Pomnóżmy jego skrajne i średnie wyrazy. Wtedy system przyjmie postać:

Pomnóżmy pierwsze równanie przez −3 i otwórzmy nawiasy w drugim:

Dodajmy teraz oba równania. W wyniku dodania tych równań otrzymujemy równość z zerem po obu stronach:

Okazuje się, że system ma niezliczoną ilość rozwiązań.

Ale nie możemy po prostu brać dowolnych wartości z nieba X I y. Możemy podać jedną z wartości, a druga zostanie określona w zależności od wartości, którą podamy. Na przykład niech X= 2 . Podstawmy tę wartość do systemu:

W wyniku rozwiązania jednego z równań wartość dla y, co spełni oba równania:

Powstała para wartości (2; −2) spełni wymagania układu:

Znajdźmy inną parę wartości. Pozwalać X= 4. Podstawmy tę wartość do systemu:

Na oko można stwierdzić, że wartość y równa się zeru. Następnie otrzymujemy parę wartości (4; 0) spełniającą nasz system:

Przykład 8. Rozwiąż następujący układ równań metodą dodawania:

Pomnóż pierwsze równanie przez 6, a drugie przez 12

Przepiszmy to, co zostało:

Pomnóżmy pierwsze równanie przez -1. Wtedy system przyjmie postać:

Dodajmy teraz oba równania. W wyniku dodawania powstaje równanie 6 B= 48, którego pierwiastek wynosi 8. Zastąp B do pierwszego równania i znajdź A

Układ równań liniowych z trzema zmiennymi

Równanie liniowe z trzema zmiennymi zawiera trzy zmienne ze współczynnikami, a także wyraz wolny. W formie kanonicznej można to zapisać następująco:

topór + by + cz = re

Równanie to ma niezliczoną ilość rozwiązań. Nadając dwóm zmiennym różne wartości, można znaleźć trzecią wartość. Rozwiązaniem w tym przypadku jest trójka wartości ( X; y; z), co zamienia równanie w tożsamość.

Jeśli zmienne x, y, z są ze sobą powiązane trzema równaniami, wówczas powstaje układ trzech równań liniowych z trzema zmiennymi. Do rozwiązania takiego układu można zastosować te same metody, które obowiązują w przypadku równań liniowych z dwiema zmiennymi: metodę podstawienia i metodę dodawania.

Przykład 1. Rozwiąż następujący układ równań metodą podstawieniową:

Wyraźmy to w trzecim równaniu X. Wtedy system przyjmie postać:

Teraz dokonajmy podstawienia. Zmienny X jest równe wyrażeniu 3 − 2y − 2z . Podstawmy to wyrażenie do pierwszego i drugiego równania:

Otwórzmy nawiasy w obu równaniach i przedstawmy podobne wyrażenia:

Dotarliśmy do układu równań liniowych z dwiema zmiennymi. W takim przypadku wygodnie jest zastosować metodę dodawania. W efekcie zmienna y zniknie i będziemy mogli znaleźć wartość zmiennej z

Teraz znajdźmy wartość y. Aby to zrobić, wygodnie jest użyć równania − y+ z= 4. Zastąp do niego wartość z

Teraz znajdźmy wartość X. Aby to zrobić, wygodnie jest użyć równania X= 3 − 2y − 2z . Podstawmy w nim wartości y I z

Zatem trójka wartości (3; −2; 2) jest rozwiązaniem naszego układu. Sprawdzając upewniamy się, że wartości te spełniają system:

Przykład 2. Rozwiąż układ metodą dodawania

Dodajmy pierwsze równanie do drugiego, pomnożone przez -2.

Jeśli drugie równanie zostanie pomnożone przez -2, przyjmie postać −6X+ 6y- 4z = −4 . Dodajmy to teraz do pierwszego równania:

Widzimy, że w wyniku elementarnych przekształceń została wyznaczona wartość zmiennej X. Jest równy jeden.

Wróćmy do głównego systemu. Dodajmy drugie równanie do trzeciego, pomnożone przez -1. Jeśli trzecie równanie zostanie pomnożone przez -1, przyjmie postać −4X + 5y − 2z = −1 . Dodajmy to teraz do drugiego równania:

Mamy równanie x− 2y= −1 . Podstawmy do niego wartość X które znaleźliśmy wcześniej. Następnie możemy określić wartość y

Teraz znamy znaczenia X I y. Dzięki temu możesz określić wartość z. Skorzystajmy z jednego z równań zawartych w układzie:

Zatem potrójna wartość (1; 1; 1) jest rozwiązaniem naszego układu. Sprawdzając upewniamy się, że wartości te spełniają system:

Zagadnienia tworzenia układów równań liniowych

Zadanie układania układów równań rozwiązuje się poprzez wprowadzenie kilku zmiennych. Następnie zestawiane są równania w oparciu o warunki problemu. Z opracowanych równań tworzą układ i rozwiązują go. Po rozwiązaniu układu należy sprawdzić, czy jego rozwiązanie spełnia warunki zadania.

Problem 1. Samochód Wołga wyjechał z miasta do kołchozu. Wróciła inną drogą, o 5 km krótszą od pierwszej. W sumie samochód przejechał w obie strony 35 km. Ile kilometrów ma długość każdej drogi?

Rozwiązanie

Pozwalać X- długość pierwszej drogi, y- długość drugiej. Jeśli samochód przejechał w obie strony 35 km, pierwsze równanie można zapisać jako X+ y= 35. Równanie to opisuje sumę długości obu dróg.

Mówi się, że samochód wracał drogą o 5 km krótszą od pierwszej. Następnie drugie równanie można zapisać jako X− y= 5. Z tego równania wynika, że ​​różnica długości dróg wynosi 5 km.

Lub drugie równanie można zapisać jako X= y+ 5. Będziemy korzystać z tego równania.

Ponieważ zmienne X I y w obu równaniach oznaczamy tę samą liczbę, to możemy z nich ułożyć układ:

Rozwiążmy ten układ, korzystając z niektórych z wcześniej zbadanych metod. W takim przypadku wygodnie jest zastosować metodę podstawienia, ponieważ w drugim równaniu zmienna X już wyrażone.

Zastąp drugie równanie pierwszym i znajdź y

Zastąpmy znalezioną wartość y w drugim równaniu X= y+ 5 i znajdziemy X

Za pomocą zmiennej wyznaczono długość pierwszej drogi X. Teraz odkryliśmy jego znaczenie. Zmienny X wynosi 20. Oznacza to, że długość pierwszej drogi wynosi 20 km.

A długość drugiej drogi oznaczono y. Wartość tej zmiennej wynosi 15. Oznacza to, że długość drugiej drogi wynosi 15 km.

Sprawdźmy. Najpierw upewnijmy się, że system został rozwiązany poprawnie:

Sprawdźmy teraz, czy rozwiązanie (20; 15) spełnia warunki zadania.

Mówiono, że samochód przejechał w sumie 35 km w obie strony. Dodajemy długości obu dróg i upewniamy się, że rozwiązanie (20; 15) spełnia warunek: 20 km + 15 km = 35 km

Następujący warunek: samochód wrócił inną drogą, krótszą o 5 km od pierwszej . Widzimy, że rozwiązanie (20; 15) również spełnia ten warunek, gdyż 15 km jest krótsze od 20 km o 5 km: 20 km - 15 km = 5 km

Podczas tworzenia układu ważne jest, aby zmienne reprezentowały te same liczby we wszystkich równaniach wchodzących w skład tego układu.

Zatem nasz układ zawiera dwa równania. Równania te z kolei zawierają zmienne X I y, które w obu równaniach reprezentują te same liczby, a mianowicie długości dróg wynoszące 20 km i 15 km.

Problem 2. Na platformę załadowano podkłady dębowe i sosnowe, łącznie 300 podkładów. Wiadomo, że wszystkie podkłady dębowe ważyły ​​o 1 tonę mniej niż wszystkie podkłady sosnowe. Oblicz, ile podkładów dębowych i sosnowych było osobno, jeśli każdy podkład dębowy ważył 46 kg, a każdy podkład sosnowy 28 kg.

Rozwiązanie

Pozwalać X dąb i y Na platformę załadowano podkłady sosnowe. Jeśli w sumie było 300 podkładów, pierwsze równanie można zapisać jako x+y = 300 .

Wszystkie podkłady dębowe ważyły ​​46 X kg, a sosnowe 28 y kg. Ponieważ podkłady dębowe ważyły ​​​​o 1 tonę mniej niż podkłady sosnowe, drugie równanie można zapisać jako 28y- 46X= 1000 . Z równania tego wynika, że ​​różnica mas pomiędzy podkładami dębowymi i sosnowymi wynosi 1000 kg.

Tony przeliczono na kilogramy, ponieważ masę podkładów dębowych i sosnowych mierzono w kilogramach.

W rezultacie otrzymujemy dwa równania tworzące układ

Rozwiążmy ten system. Wyraźmy to w pierwszym równaniu X. Wtedy system przyjmie postać:

Zastąp pierwsze równanie drugim i znajdź y

Zastąpmy y w równanie X= 300 − y i dowiedz się, co to jest X

Oznacza to, że na platformę załadowano 100 podkładów dębowych i 200 sosnowych.

Sprawdźmy, czy rozwiązanie (100; 200) spełnia warunki zadania. Najpierw upewnijmy się, że system został rozwiązany poprawnie:

Mówiono, że łącznie było 300 podkładów. Sumujemy liczbę podkładów dębowych i sosnowych i upewniamy się, że rozwiązanie (100; 200) spełnia warunek: 100 + 200 = 300.

Następujący warunek: wszystkie podkłady dębowe ważyły ​​o 1 tonę mniej niż wszystkie podkłady sosnowe . Widzimy, że rozwiązanie (100; 200) również spełnia ten warunek, ponieważ 46 × 100 kg podkładów dębowych jest lżejsze niż 28 × 200 kg podkładów sosnowych: 5600 kg - 4600 kg = 1000 kg.

Problem 3. Wzięliśmy trzy kawałki stopu miedzi i niklu w proporcjach wagowych 2: 1, 3: 1 i 5: 1. Stopiono z nich kawałek o masie 12 kg, w którym stosunek zawartości miedzi do niklu wynosił 4:1. Znajdź masę każdego pierwotnego kawałka, jeśli masa pierwszego jest dwukrotnie większa od masy drugiego.

Metoda Gaussa ma wiele wad: nie można stwierdzić, czy system jest spójny, czy nie, dopóki nie zostaną przeprowadzone wszystkie niezbędne przekształcenia w metodzie Gaussa; Metoda Gaussa nie jest odpowiednia dla układów ze współczynnikami literowymi.

Rozważmy inne metody rozwiązywania układów równań liniowych. Metody te wykorzystują koncepcję rangi macierzy i sprowadzają rozwiązanie dowolnego układu spójnego do rozwiązania układu, do którego ma zastosowanie reguła Cramera.

Przykład 1. Znajdź rozwiązanie ogólne poniższego układu równań liniowych, wykorzystując podstawowy układ rozwiązań zredukowanego układu jednorodnego i szczególne rozwiązanie układu niejednorodnego.

1. Tworzenie macierzy A i rozbudowana matryca systemu (1)

2. Poznaj system (1) dla wspólnoty. Aby to zrobić, znajdujemy szeregi macierzy A i https://pandia.ru/text/78/176/images/image006_90.gif"width="17" height="26 src=">). Jeśli się okaże, że to system (1) niekompatybilny. Jeśli to dostaniemy , to ten układ jest spójny i rozwiążemy go. (Badanie zgodności opiera się na twierdzeniu Kroneckera-Capelliego).

A. Znaleźliśmy rA.

Znaleźć rA, rozważymy sekwencyjnie niezerowe molle pierwszego, drugiego itd. rzędów macierzy A i otaczających ich nieletnich.

M1=1≠0 (bierzemy 1 z lewego górnego rogu macierzy A).

Graniczymy M1 drugi wiersz i druga kolumna tej macierzy. . Kontynuujemy granicę M1 druga linia i trzecia kolumna..gif" szerokość="37" wysokość="20 src=">. Teraz graniczymy z niezerowym mollem M2′ drugie zamówienie.

Mamy: (ponieważ pierwsze dwie kolumny są takie same)

(ponieważ druga i trzecia linia są proporcjonalne).

Widzimy to rA=2, a jest podstawą małej macierzy A.

B. Znaleźliśmy.

Dość podstawowe drobne M2′ matryce A obramuj kolumną wolnych terminów i wszystkimi wierszami (mamy tylko ostatni wiersz).

. Wynika, że M3′′ pozostaje podstawowym mollem macierzy https://pandia.ru/text/78/176/images/image019_33.gif" szerokość="168 wysokość=75" wysokość="75"> (2)

Ponieważ M2′- podstawa mała macierzy A systemy (2) , to ten system jest równoważny systemowi (3) , składający się z dwóch pierwszych równań układu (2) (Do M2′ znajduje się w dwóch pierwszych wierszach macierzy A).

(3)

Od podstawowego drobnego https://pandia.ru/text/78/176/images/image021_29.gif" szerokość="153" wysokość="51"> (4)

W tym układzie istnieją dwie wolne niewiadome ( x2 I x4 ). Dlatego FSR systemy (4) składa się z dwóch rozwiązań. Aby je znaleźć, przypisujemy wolne niewiadome w (4) najpierw wartości x2=1 , x4=0 , i wtedy - x2=0 , x4=1 .

Na x2=1 , x4=0 otrzymujemy:

.

Ten system już to zrobił Jedyną rzeczą rozwiązanie (można je znaleźć korzystając z reguły Cramera lub dowolnej innej metody). Odejmując pierwsze od drugiego równania, otrzymujemy:

Jej rozwiązaniem będzie x1= -1 , x3=0 . Biorąc pod uwagę wartości x2 I x4 , które dodaliśmy, otrzymujemy pierwsze rozwiązanie fundamentalne układu (2) : .

Teraz wierzymy (4) x2=0 , x4=1 . Otrzymujemy:

.

Rozwiązujemy ten układ korzystając z twierdzenia Cramera:

.

Otrzymujemy drugie rozwiązanie podstawowe układu (2) : .

Rozwiązania β1 , β2 i makijaż FSR systemy (2) . Wtedy będzie jego ogólne rozwiązanie

γ= C1 β1+С2β2=С1(-1, 1, 0, 0)+С2(5, 0, 4, 1)=(-С1+5С2, С1, 4С2, С2)

Tutaj C1 , C2 – dowolne stałe.

4. Znajdźmy takiego prywatny rozwiązanie system heterogeniczny(1) . Jak w ust 3 zamiast systemu (1) Rozważmy równoważny system (5) , składający się z dwóch pierwszych równań układu (1) .

(5)

Przesuwamy wolne niewiadome na prawą stronę x2 I x4.

(6)

Dajmy wolne niewiadome x2 I x4 dowolne wartości, np. x2=2 , x4=1 i włóż je (6) . Weźmy system

Układ ten ma unikalne rozwiązanie (ponieważ jego wyznacznik M2′0). Rozwiązując to (wykorzystując twierdzenie Cramera lub metodę Gaussa) otrzymujemy x1=3 , x3=3 . Biorąc pod uwagę wartości wolnych niewiadomych x2 I x4 , otrzymujemy szczególne rozwiązanie układu niejednorodnego(1)α1=(3,2,3,1).

5. Teraz pozostaje tylko to zapisać rozwiązanie ogólne α układu niejednorodnego(1) : jest równa sumie rozwiązanie prywatne ten system i ogólne rozwiązanie jego zredukowanego układu jednorodnego (2) :

α=α1+γ=(3, 2, 3, 1)+(-С1+5С2, С1, 4С2, С2).

To znaczy: (7)

6. Badanie. Aby sprawdzić, czy poprawnie rozwiązałeś system (1) , potrzebujemy ogólnego rozwiązania (7) zastąpić w (1) . Jeśli każde równanie zamienia się w tożsamość ( C1 I C2 muszą zostać zniszczone), wówczas rozwiązanie zostanie znalezione prawidłowo.

Zastąpimy (7) na przykład tylko ostatnie równanie układu (1) (X1 + X2 + X3 ‑9 X4 =‑1) .

Otrzymujemy: (3–С1+5С2)+(2+С1)+(3+4С2)–9(1+С2)=–1

(С1–С1)+(5С2+4С2–9С2)+(3+2+3–9)=–1

Gdzie –1=–1. Mamy tożsamość. Robimy to ze wszystkimi innymi równaniami układu (1) .

Komentarz. Sprawdzanie jest zazwyczaj dość kłopotliwe. Można zalecić następującą „częściową kontrolę”: w ogólnym rozwiązaniu układu (1) przypisz pewne wartości dowolnym stałym i podstaw wynikowe rozwiązanie częściowe tylko do odrzuconych równań (tj. do równań z (1) , które nie zostały uwzględnione (5) ). Jeśli uda się ustalić tożsamość bardziej prawdopodobne, rozwiązanie systemowe (1) znalezione poprawnie (jednak takie sprawdzenie nie daje całkowitej gwarancji poprawności!). Na przykład, jeśli w (7) umieścić C2=- 1 , C1=1, wtedy otrzymujemy: x1=-3, x2=3, x3=-1, x4=0. Podstawiając do ostatniego równania układu (1) mamy: - 3+3 - 1 - 9∙0= - 1 , tj. –1=–1. Mamy tożsamość.

Przykład 2. Znajdź rozwiązanie ogólne układu równań liniowych (1) , wyrażając podstawowe niewiadome w postaci wolnych.

Rozwiązanie. Jak w Przykład 1, układaj macierze A i https://pandia.ru/text/78/176/images/image010_57.gif"width="156" height="50"> tych macierzy. Teraz zostawiamy tylko te równania układu (1) , których współczynniki zawarte są w tym mollu podstawowym (czyli mamy dwa pierwsze równania) i rozważamy składający się z nich układ, równoważny układowi (1).

Przeniesiemy wolne niewiadome na prawą stronę tych równań.

system (9) Rozwiązujemy metodą Gaussa, uznając prawe strony za wyrazy swobodne.

https://pandia.ru/text/78/176/images/image035_21.gif" szerokość="202 wysokość=106" wysokość="106">

Opcja 2.

https://pandia.ru/text/78/176/images/image039_16.gif" szerokość="192" wysokość="106 src=">

Opcja 4.

https://pandia.ru/text/78/176/images/image042_14.gif" szerokość="172" wysokość="80">

Opcja 5.

https://pandia.ru/text/78/176/images/image044_12.gif" szerokość="179 wysokość=106" wysokość="106">

Opcja 6.

https://pandia.ru/text/78/176/images/image046_11.gif" szerokość="195" wysokość="106">

Jak wynika z Twierdzenie Cramera, przy rozwiązywaniu układu równań liniowych mogą wystąpić trzy przypadki:

Przypadek pierwszy: układ równań liniowych ma unikalne rozwiązanie

(system jest spójny i określony)

Przypadek drugi: układ równań liniowych ma nieskończoną liczbę rozwiązań

(system jest spójny i niepewny)

** ,

te. współczynniki niewiadomych i wyrazy wolne są proporcjonalne.

Przypadek trzeci: układ równań liniowych nie ma rozwiązań

(system jest niespójny)

A więc system M równania liniowe z N zwane zmiennymi nie wspólne, jeśli nie ma jednego rozwiązania, i wspólny, jeśli ma co najmniej jedno rozwiązanie. Nazywa się równoczesny układ równań, który ma tylko jedno rozwiązanie niektórzy i więcej niż jeden – niepewny.

Przykłady rozwiązywania układów równań liniowych metodą Cramera

Niech będzie dany system

.

Na podstawie twierdzenia Cramera

………….
,

Gdzie
-

wyznacznik systemu. Pozostałe wyznaczniki uzyskujemy zastępując kolumnę współczynnikami odpowiedniej zmiennej (nieznanej) o terminach dowolnych:

Przykład 2.

.

Zatem system jest określony. Aby znaleźć rozwiązanie, obliczamy wyznaczniki

Korzystając ze wzorów Cramera znajdujemy:

Zatem (1; 0; -1) jest jedynym rozwiązaniem tego układu.

Aby sprawdzić rozwiązania układów równań 3 X 3 i 4 X 4, możesz skorzystać z kalkulatora online, korzystając z metody rozwiązywania Cramera.

Jeśli w układzie równań liniowych nie ma zmiennych w jednym lub większej liczbie równań, to w wyznaczniku odpowiednie elementy są równe zeru! To jest następny przykład.

Przykład 3. Rozwiąż układ równań liniowych metodą Cramera:

.

Rozwiązanie. Znajdujemy wyznacznik układu:

Przyjrzyj się uważnie układowi równań i wyznacznikowi układu i powtórz odpowiedź na pytanie, w jakich przypadkach jeden lub więcej elementów wyznacznika jest równe zero. Zatem wyznacznik nie jest równy zero, zatem układ jest określony. Aby znaleźć rozwiązanie, obliczamy wyznaczniki niewiadomych

Korzystając ze wzorów Cramera znajdujemy:

Zatem rozwiązaniem układu jest (2; -1; 1).

6. Ogólny układ liniowych równań algebraicznych. Metoda Gaussa.

Jak pamiętamy, reguła Cramera i metoda macierzowa nie nadają się w przypadkach, gdy układ ma nieskończenie wiele rozwiązań lub jest niespójny. Metoda Gaussa – najpotężniejsze i wszechstronne narzędzie do znajdowania rozwiązań dowolnego układu równań liniowych, Który w każdym przypadku doprowadzi nas do odpowiedzi! Sam algorytm metody działa tak samo we wszystkich trzech przypadkach. Jeśli metoda Cramera i metoda macierzowa wymagają znajomości wyznaczników, to do zastosowania metody Gaussa wystarczy znajomość działań arytmetycznych, co czyni ją przystępną nawet dla uczniów szkół podstawowych.

Na początek usystematyzujmy trochę wiedzy o układach równań liniowych. Układ równań liniowych może:

1) Mieć unikalne rozwiązanie.
2) Mają nieskończenie wiele rozwiązań.
3) Nie mają rozwiązań (być nie wspólne).

Metoda Gaussa jest najpotężniejszym i najbardziej uniwersalnym narzędziem do znalezienia rozwiązania każdy układy równań liniowych. Jak pamiętamy, Reguła Cramera i metoda macierzowa są nieodpowiednie w przypadkach, gdy układ ma nieskończenie wiele rozwiązań lub jest niespójny. Oraz metoda sekwencyjnej eliminacji niewiadomych W każdym razie doprowadzi nas do odpowiedzi! W tej lekcji ponownie rozważymy metodę Gaussa dla przypadku nr 1 (jedyne rozwiązanie układu), artykuł poświęcony jest sytuacjom z punktów nr 2-3. Zwracam uwagę, że algorytm samej metody działa tak samo we wszystkich trzech przypadkach.

Wróćmy do najprostszego systemu z lekcji Jak rozwiązać układ równań liniowych?
i rozwiązać go metodą Gaussa.

Pierwszym krokiem jest zapisanie rozbudowana matryca systemu:
. Myślę, że każdy może zobaczyć, według jakiej zasady zapisywane są współczynniki. Pionowa linia wewnątrz matrycy nie ma żadnego znaczenia matematycznego – jest po prostu przekreśleniem dla ułatwienia projektowania.

Odniesienie:Polecam pamiętać warunki algebra liniowa. Matryca systemu jest macierzą złożoną wyłącznie ze współczynników niewiadomych, w tym przykładzie macierzą układu: . Rozszerzona matryca systemu– jest to ta sama macierz układu plus kolumna wolnych terminów, w tym przypadku: . Dla uproszczenia każdą z macierzy można po prostu nazwać macierzą.

Po napisaniu rozszerzonej macierzy systemu należy wykonać z nią pewne działania, które są również nazywane elementarne przemiany.

Istnieją następujące przekształcenia elementarne:

1) Smyczki matryce można przearanżować w niektórych miejscach. Na przykład w rozważanej macierzy możesz bezboleśnie zmienić układ pierwszego i drugiego wiersza:

2) Jeżeli w macierzy są (lub pojawiły się) proporcjonalne (w szczególnym przypadku - identyczne) wiersze, to należy usuwać z macierzy wszystkie te wiersze z wyjątkiem jednego. Rozważmy na przykład macierz . W tej macierzy ostatnie trzy wiersze są proporcjonalne, dlatego wystarczy pozostawić tylko jeden z nich: .

3) Jeżeli podczas przekształceń w macierzy pojawia się wiersz zerowy, to też powinien tak być usuwać. Nie będę oczywiście rysować, linia zerowa to linia, w której wszystkie zera.

4) Wiersz macierzy może być mnożyć (dzielić) na dowolny numer niezerowy. Rozważmy na przykład macierz . W tym przypadku wskazane jest podzielenie pierwszej linii przez –3 i pomnożenie drugiej linii przez 2: . Akcja ta jest bardzo przydatna, gdyż ułatwia dalsze przekształcenia macierzy.

5) Ta transformacja sprawia najwięcej trudności, ale tak naprawdę nie ma też nic skomplikowanego. Do rzędu macierzy można dodaj kolejny ciąg pomnożony przez liczbę, różny od zera. Spójrzmy na naszą macierz na praktycznym przykładzie: . Najpierw opiszę bardzo szczegółowo transformację. Pomnóż pierwszą linię przez –2: , I do drugiej linii dodajemy pierwszą linię pomnożoną przez –2: . Teraz pierwszą linię można podzielić „wstecz” przez –2: . Jak widać, linia, która jest DODANA LI – nie uległo zmianie. Zawsze zmienia się linia DO KTÓREGO JEST DODAWANA Ut.

W praktyce oczywiście nie piszą tego tak szczegółowo, ale piszą krótko:

Jeszcze raz: do drugiej linii dodano pierwszą linię pomnożoną przez –2. Wiersz jest zwykle mnożony ustnie lub w wersji roboczej, a proces obliczeń w myślach przebiega mniej więcej tak:

„Przepisuję macierz i przepisuję pierwszą linijkę: »

"Pierwsza kolumna. Na dole muszę uzyskać zero. Dlatego mnożę tę na górze przez –2: , a pierwszą dodaję do drugiej linii: 2 + (–2) = 0. Wynik zapisuję w drugiej linii: »

„Teraz druga kolumna. Na górze mnożę -1 przez -2: . Pierwszy dodaję do drugiej linii: 1 + 2 = 3. Wynik zapisuję w drugiej linii: »

„I trzecia kolumna. Na górze mnożę -5 przez -2: . Pierwszy dodaję do drugiego wiersza: –7 + 10 = 3. Wynik zapisuję w drugim wierszu: »

Proszę dokładnie zrozumieć ten przykład i zrozumieć algorytm obliczeń sekwencyjnych, jeśli to rozumiesz, to metoda Gaussa jest praktycznie w twojej kieszeni. Ale oczywiście nadal będziemy pracować nad tą transformacją.

Przekształcenia elementarne nie zmieniają rozwiązania układu równań

! UWAGA: uważane za manipulacje nie można użyć, jeśli zaproponowano ci zadanie, w którym macierze są podawane „same w sobie”. Na przykład w przypadku „klasycznego” operacje na macierzach W żadnym wypadku nie należy przestawiać czegokolwiek wewnątrz macierzy!

Wróćmy do naszego systemu. Jest praktycznie rozebrany na kawałki.

Zapiszmy rozszerzoną macierz układu i korzystając z przekształceń elementarnych sprowadźmy ją do postaci widok schodkowy:

(1) Pierwsza linia została dodana do drugiej linii, pomnożona przez –2. I jeszcze raz: dlaczego mnożymy pierwszą linię przez –2? Aby uzyskać zero na dole, co oznacza pozbycie się jednej zmiennej w drugiej linii.

(2) Podziel drugą linię przez 3.

Cel przekształceń elementarnych – sprowadź macierz do postaci krokowej: . Projektując zadanie, po prostu zaznaczają „schody” prostym ołówkiem, a także zakreślają liczby znajdujące się na „stopniach”. Sam termin „widok schodkowy” nie jest całkowicie teoretyczny; w literaturze naukowej i edukacyjnej jest często nazywany widok trapezowy Lub widok trójkątny.

W wyniku elementarnych przekształceń otrzymaliśmy równowartość oryginalny układ równań:

Teraz system należy „rozwinąć” w przeciwnym kierunku - proces ten nazywa się od dołu do góry odwrotność metody Gaussa.

W dolnym równaniu mamy już gotowy wynik: .

Rozważmy pierwsze równanie układu i podstawmy do niego znaną już wartość „y”:

Rozważmy najczęstszą sytuację, gdy metoda Gaussa wymaga rozwiązania układu trzech równań liniowych z trzema niewiadomymi.

Przykład 1

Rozwiąż układ równań metodą Gaussa:

Napiszmy rozszerzoną macierz układu:

Teraz od razu narysuję wynik, do którego dojdziemy podczas rozwiązania:

I powtarzam, naszym celem jest doprowadzenie macierzy do postaci krokowej za pomocą elementarnych przekształceń. Gdzie zacząć?

Najpierw spójrz na liczbę w lewym górnym rogu:

Powinien prawie zawsze tu być jednostka. Ogólnie rzecz biorąc, wystarczy –1 (a czasami inne liczby), ale jakoś tradycyjnie tak się złożyło, że zwykle umieszczano je w tym miejscu. Jak zorganizować jednostkę? Patrzymy na pierwszą kolumnę - mamy gotową jednostkę! Transformacja pierwsza: zamień pierwszą i trzecią linię:

Teraz pierwsza linia pozostanie niezmieniona aż do końca rozwiązania. Teraz dobrze.

Jednostka w lewym górnym rogu jest zorganizowana. Teraz musisz uzyskać zera w tych miejscach:

Zera otrzymujemy stosując „trudną” transformację. Najpierw zajmujemy się drugą linią (2, –1, 3, 13). Co należy zrobić, aby na pierwszym miejscu pojawiło się zero? Potrzebować do drugiej linii dodaj pierwszą linię pomnożoną przez –2. W myślach lub w szkicu pomnóż pierwszą linię przez –2: (–2, –4, 2, –18). I konsekwentnie przeprowadzamy (znowu w myślach lub na szkicu) dodawanie, do drugiej linii dodajemy pierwszą linię, już pomnożoną przez –2:

Wynik zapisujemy w drugiej linii:

W ten sam sposób postępujemy z trzecią linią (3, 2, –5, –1). Aby uzyskać zero na pierwszej pozycji, potrzebujesz do trzeciej linii dodaj pierwszą linię pomnożoną przez –3. W myślach lub w szkicu pomnóż pierwszą linię przez –3: (–3, –6, 3, –27). I do trzeciej linii dodajemy pierwszą linię pomnożoną przez –3:

Wynik zapisujemy w trzeciej linii:

W praktyce czynności te najczęściej wykonywane są ustnie i spisywane w jednym kroku:

Nie trzeba liczyć wszystkiego na raz i w tym samym czasie. Kolejność obliczeń i „wpisywania” wyników spójny i zwykle jest tak: najpierw przepisujemy pierwszą linijkę i powoli się zaciągamy - KONSEKWENCJONALNIE i UWAŻNIE:


Omówiłem już proces myślowy samych obliczeń powyżej.

W tym przykładzie jest to łatwe do zrobienia; dzielimy drugą linię przez –5 (ponieważ wszystkie liczby w niej są podzielne przez 5 bez reszty). Jednocześnie dzielimy trzecią linię przez –2, bo im mniejsze liczby, tym prostsze rozwiązanie:

Na ostatnim etapie elementarnych przekształceń musisz tutaj uzyskać kolejne zero:

Dla tego do trzeciej linii dodajemy drugą linię pomnożoną przez –2:


Spróbuj sam wymyślić tę akcję - pomnóż w myślach drugą linię przez –2 i wykonaj dodawanie.

Ostatnią wykonaną akcją jest fryzura wyniku, podziel trzecią linię przez 3.

W wyniku elementarnych przekształceń otrzymano równoważny układ równań liniowych:

Fajny.

Teraz wchodzi w grę odwrotność metody Gaussa. Równania „rozwijają się” od dołu do góry.

W trzecim równaniu mamy już gotowy wynik:

Spójrzmy na drugie równanie: . Znaczenie słowa „zet” jest już znane, a zatem:

I na koniec pierwsze równanie: . „Igrek” i „zet” są znane, to tylko kwestia drobiazgów:

Odpowiedź:

Jak już kilkakrotnie zaznaczano, dla każdego układu równań możliwe i konieczne jest sprawdzenie znalezionego rozwiązania, na szczęście jest to łatwe i szybkie.

Przykład 2

To jest przykład samodzielnego rozwiązania, próbka finalnego projektu i odpowiedź na koniec lekcji.

Warto zauważyć, że Twój postęp decyzji może nie pokrywać się z moim procesem decyzyjnym, i jest to cecha metody Gaussa. Ale odpowiedzi muszą być takie same!

Przykład 3

Rozwiązać układ równań liniowych metodą Gaussa

Zapiszmy rozszerzoną macierz układu i za pomocą elementarnych przekształceń sprowadźmy ją do postaci krokowej:

Patrzymy na lewy górny „krok”. Powinniśmy go tam mieć. Problem polega na tym, że w pierwszej kolumnie w ogóle nie ma jednostek, więc zmiana kolejności wierszy niczego nie rozwiąże. W takich przypadkach jednostka musi być zorganizowana przy użyciu transformacji elementarnej. Zwykle można to zrobić na kilka sposobów. Ja to zrobiłem:
(1) Do pierwszej linii dodajemy drugą linię pomnożoną przez –1. Oznacza to, że mentalnie pomnożyliśmy drugą linię przez –1 i dodaliśmy pierwszą i drugą linię, podczas gdy druga linia się nie zmieniła.

Teraz w lewym górnym rogu znajduje się „minus jeden”, co nam całkiem odpowiada. Każdy, kto chce otrzymać +1, może wykonać dodatkowy ruch: pomnożyć pierwszą linię przez –1 (zmienić jej znak).

(2) Do drugiej linii dodano pierwszą linię pomnożoną przez 5. Pierwszą linię pomnożoną przez 3 dodano do trzeciej linii.

(3) Pierwsza linia została pomnożona przez –1, w zasadzie dotyczy to piękna. Zmieniono także znak trzeciej linii i przesunięto go na drugie miejsce, dzięki czemu na drugim „kroku” mieliśmy już wymaganą jednostkę.

(4) Druga linia została dodana do trzeciej linii, pomnożona przez 2.

(5) Trzecia linia została podzielona przez 3.

Zły znak wskazujący na błąd w obliczeniach (rzadziej literówkę) to „zły” wynik końcowy. To znaczy, jeśli mamy coś takiego jak poniżej i odpowiednio , to z dużym prawdopodobieństwem można powiedzieć, że przy przekształceniach elementarnych popełniono błąd.

My obciążamy odwrotnie, przy projektowaniu przykładów często nie przepisuje się samego układu, ale równania „bierze się bezpośrednio z danej macierzy”. Przypominam, że odwrotny skok działa od dołu do góry. Tak, oto prezent:

Odpowiedź: .

Przykład 4

Rozwiązać układ równań liniowych metodą Gaussa

To jest przykład do samodzielnego rozwiązania, jest nieco bardziej skomplikowany. Nie ma problemu, jeśli ktoś się pomyli. Pełne rozwiązanie i przykładowy projekt na końcu lekcji. Twoje rozwiązanie może różnić się od mojego.

W ostatniej części przyjrzymy się niektórym cechom algorytmu Gaussa.
Pierwszą cechą jest to, że czasami w równaniach układu brakuje niektórych zmiennych, na przykład:

Jak poprawnie napisać rozszerzoną macierz systemu? Mówiłem już o tym punkcie na zajęciach. Reguła Cramera. Metoda matrycowa. W rozszerzonej macierzy systemu w miejsce brakujących zmiennych wstawiamy zera:

Nawiasem mówiąc, jest to dość łatwy przykład, ponieważ pierwsza kolumna ma już jedno zero, a do wykonania jest mniej elementarnych transformacji.

Druga cecha jest taka. We wszystkich rozważanych przykładach umieściliśmy „kroki” albo –1, albo +1. Czy mogą być tam inne numery? W niektórych przypadkach mogą. Rozważ system: .

Tutaj, w lewym górnym „kroku”, mamy dwójkę. Ale zauważamy, że wszystkie liczby w pierwszej kolumnie są podzielne przez 2 bez reszty - a druga to dwa i sześć. A te dwa w lewym górnym rogu będą nam odpowiadać! W pierwszym kroku należy wykonać następujące przekształcenia: dodać do drugiej linii pierwszą linię pomnożoną przez –1; do trzeciej linii dodaj pierwszą linię pomnożoną przez –3. W ten sposób uzyskamy wymagane zera w pierwszej kolumnie.

Lub inny konwencjonalny przykład: . Tutaj trójka w drugim „kroku” również nam odpowiada, ponieważ 12 (miejsce, w którym musimy uzyskać zero) jest podzielne przez 3 bez reszty. Należy przeprowadzić następującą transformację: dodać drugą linię do trzeciej linii, pomnożoną przez –4, w wyniku czego otrzymamy potrzebne nam zero.

Metoda Gaussa jest uniwersalna, ale ma jedną osobliwość. Rozwiązywania układów innymi metodami (metoda Cramera, metoda macierzowa) można śmiało nauczyć się dosłownie za pierwszym razem – mają one bardzo rygorystyczny algorytm. Ale żeby mieć pewność co do metody Gaussa, trzeba ją opanować i rozwiązać przynajmniej 5-10 układów. Dlatego na początku może pojawić się zamieszanie i błędy w obliczeniach i nie ma w tym nic niezwykłego ani tragicznego.

Za oknem deszczowa jesienna pogoda.... Dlatego dla każdego, kto ma ochotę na bardziej złożony przykład do samodzielnego rozwiązania:

Przykład 5

Rozwiąż układ czterech równań liniowych z czterema niewiadomymi, stosując metodę Gaussa.

Takie zadanie nie jest w praktyce tak rzadkie. Myślę, że nawet czajniczek, który dokładnie przestudiował tę stronę, zrozumie algorytm intuicyjnego rozwiązania takiego systemu. Zasadniczo wszystko jest takie samo - jest tylko więcej akcji.

Na lekcji omówione zostaną przypadki, gdy układ nie ma rozwiązań (niespójny) lub ma nieskończenie wiele rozwiązań Niekompatybilne systemy i systemy ze wspólnym rozwiązaniem. Tam możesz naprawić rozważany algorytm metody Gaussa.

Życzę Ci sukcesu!

Rozwiązania i odpowiedzi:

Przykład 2: Rozwiązanie: Zapiszmy rozszerzoną macierz układu i za pomocą przekształceń elementarnych sprowadźmy ją do postaci krokowej.


Wykonane przekształcenia elementarne:
(1) Pierwsza linia została dodana do drugiej linii, pomnożona przez –2. Pierwsza linia została dodana do trzeciej linii, pomnożona przez –1. Uwaga! Tutaj możesz pokusić się o odjęcie pierwszej linii od trzeciej linii; zdecydowanie nie radzę tego odejmować – ryzyko błędu znacznie wzrasta. Po prostu złóż!
(2) Zmieniono znak drugiej linii (pomnożony przez –1). Druga i trzecia linia zostały zamienione miejscami. notatka, że na „stopniach” zadowalamy się nie tylko jednym, ale także –1, co jest jeszcze wygodniejsze.
(3) Druga linia została dodana do trzeciej linii, pomnożona przez 5.
(4) Zmieniono znak drugiej linii (pomnożony przez –1). Trzecia linia została podzielona przez 14.

Odwracać:

Odpowiedź: .

Przykład 4: Rozwiązanie: Zapiszmy rozszerzoną macierz układu i za pomocą elementarnych przekształceń sprowadźmy ją do postaci krokowej:

Wykonane konwersje:
(1) Do pierwszego wiersza dodano drugi wiersz. W ten sposób żądana jednostka jest zorganizowana w lewym górnym „kroku”.
(2) Do drugiej linii dodano pierwszą linię pomnożoną przez 7. Do trzeciej linii dodano pierwszą linię pomnożoną przez 6.

Z drugim „krokiem” wszystko się pogarsza, „kandydatami” do tego są liczby 17 i 23, a my potrzebujemy albo jednego, albo –1. Transformacje (3) i (4) będą miały na celu uzyskanie pożądanej jednostki

(3) Druga linia została dodana do trzeciej linii, pomnożona przez –1.
(4) Do drugiej linii dodano trzecią linię pomnożoną przez –3.
Otrzymano wymagany przedmiot w drugim kroku. .
(5) Druga linia została dodana do trzeciej linii i pomnożona przez 6.

W ramach zajęć Metoda Gaussa I Niekompatybilne systemy/systemy ze wspólnym rozwiązaniem rozważaliśmy niejednorodne układy równań liniowych, Gdzie Wolny Członek(który zwykle znajduje się po prawej stronie) przynajmniej jeden z równań była różna od zera.
A teraz, po dobrej rozgrzewce z ranga matrycy, będziemy nadal udoskonalać technikę elementarne przemiany NA jednorodny układ równań liniowych.
Sądząc po pierwszych akapitach, materiał może wydawać się nudny i przeciętny, jednak wrażenie to jest zwodnicze. Oprócz dalszego rozwoju technik pojawi się mnóstwo nowych informacji, dlatego prosimy nie zaniedbywać przykładów w tym artykule.

Układy równań są szeroko stosowane w sektorze gospodarczym do matematycznego modelowania różnych procesów. Na przykład przy rozwiązywaniu problemów związanych z zarządzaniem i planowaniem produkcji, tras logistycznych (problem transportu) lub rozmieszczenia sprzętu.

Układy równań wykorzystuje się nie tylko w matematyce, ale także w fizyce, chemii i biologii przy rozwiązywaniu problemów wyznaczania wielkości populacji.

Układ równań liniowych to dwa lub więcej równań z kilkoma zmiennymi, dla których konieczne jest znalezienie wspólnego rozwiązania. Taki ciąg liczb, dla którego wszystkie równania stają się prawdziwymi równościami lub dowodzą, że ciąg nie istnieje.

Równanie liniowe

Równania w postaci ax+by=c nazywane są liniowymi. Oznaczenia x, y to niewiadome, których wartość należy znaleźć, b, a to współczynniki zmiennych, c to wolny składnik równania.
Rozwiązanie równania poprzez jego wykreślenie będzie wyglądać jak linia prosta, której wszystkie punkty są rozwiązaniami wielomianu.

Rodzaje układów równań liniowych

Za najprostsze przykłady uważa się układy równań liniowych z dwiema zmiennymi X i Y.

F1(x, y) = 0 i F2(x, y) = 0, gdzie F1,2 to funkcje, a (x, y) to zmienne funkcyjne.

Rozwiązać układ równań - oznacza to znalezienie wartości (x, y), przy których układ zamienia się w prawdziwą równość lub ustalenie, że odpowiednie wartości x i y nie istnieją.

Para wartości (x, y), zapisana jako współrzędne punktu, nazywana jest rozwiązaniem układu równań liniowych.

Jeśli systemy mają jedno wspólne rozwiązanie lub nie ma żadnego rozwiązania, nazywa się je równoważnymi.

Jednorodne układy równań liniowych to układy, których prawa strona jest równa zeru. Jeżeli prawa część po znaku równości ma wartość lub jest wyrażona funkcją, to taki układ jest heterogeniczny.

Liczba zmiennych może być znacznie większa niż dwie, wtedy powinniśmy mówić o przykładzie układu równań liniowych z trzema lub więcej zmiennymi.

W obliczu systemów uczniowie zakładają, że liczba równań musi koniecznie pokrywać się z liczbą niewiadomych, ale tak nie jest. Liczba równań w układzie nie zależy od zmiennych, może być ich tyle, ile potrzeba.

Proste i złożone metody rozwiązywania układów równań

Nie ma ogólnej metody analitycznej rozwiązywania takich układów, wszystkie metody opierają się na rozwiązaniach numerycznych. Szkolny kurs matematyki szczegółowo opisuje takie metody jak permutacja, dodawanie algebraiczne, podstawienie, a także metody graficzne i macierzowe, rozwiązanie metodą Gaussa.

Głównym zadaniem nauczania metod rozwiązywania problemów jest nauczenie prawidłowej analizy systemu i znalezienia optymalnego algorytmu rozwiązania dla każdego przykładu. Najważniejsze nie jest zapamiętywanie systemu zasad i działań dla każdej metody, ale zrozumienie zasad stosowania określonej metody

Rozwiązywanie przykładów układów równań liniowych w programie nauczania ogólnego w klasie VII jest dość proste i szczegółowo wyjaśnione. W każdym podręczniku do matematyki tej sekcji poświęca się wystarczająco dużo uwagi. Rozwiązywanie przykładów układów równań liniowych metodą Gaussa i Cramera jest szerzej studiowane na pierwszych latach studiów wyższych.

Rozwiązywanie układów metodą podstawieniową

Działania metody podstawieniowej mają na celu wyrażenie wartości jednej zmiennej za pomocą drugiej. Wyrażenie podstawiamy do pozostałego równania, a następnie sprowadzamy do postaci z jedną zmienną. Czynność powtarza się w zależności od ilości niewiadomych w systemie

Podajmy rozwiązanie przykładowego układu równań liniowych klasy 7 metodą podstawieniową:

Jak widać na przykładzie zmienną x wyrażono poprzez F(X) = 7 + Y. Powstałe wyrażenie, podstawione w miejsce X do 2. równania układu, pozwoliło otrzymać w 2. równaniu jedną zmienną Y . Rozwiązanie tego przykładu jest łatwe i pozwala uzyskać wartość Y. Ostatnim krokiem jest sprawdzenie uzyskanych wartości.

Nie zawsze możliwe jest rozwiązanie przykładowego układu równań liniowych przez podstawienie. Równania mogą być złożone i wyrażenie zmiennej w kategoriach drugiej niewiadomej będzie zbyt kłopotliwe do dalszych obliczeń. Jeżeli w systemie są więcej niż 3 niewiadome, rozwiązywanie przez podstawienie również jest niewłaściwe.

Rozwiązanie przykładowego układu równań liniowych niejednorodnych:

Rozwiązanie wykorzystujące dodawanie algebraiczne

Szukając rozwiązań układów metodą dodawania, równania dodaje się termin po wyrazie i mnoży przez różne liczby. Ostatecznym celem operacji matematycznych jest równanie z jedną zmienną.

Stosowanie tej metody wymaga praktyki i obserwacji. Rozwiązywanie układu równań liniowych metodą dodawania, gdy występują 3 lub więcej zmiennych, nie jest łatwe. Dodawanie algebraiczne jest wygodne w użyciu, gdy równania zawierają ułamki zwykłe i dziesiętne.

Algorytm rozwiązania:

1. Pomnóż obie strony równania przez określoną liczbę. W wyniku operacji arytmetycznej jeden ze współczynników zmiennej powinien przyjąć wartość 1.
2. Dodaj wynikowe wyrażenie termin po terminie i znajdź jedną z niewiadomych.
3. Podstaw uzyskaną wartość do drugiego równania układu, aby znaleźć pozostałą zmienną.

Metoda rozwiązania poprzez wprowadzenie nowej zmiennej

Nową zmienną można wprowadzić, jeżeli układ wymaga znalezienia rozwiązania nie więcej niż dwóch równań, liczba niewiadomych również nie powinna przekraczać dwóch.

Metodę tę stosuje się w celu uproszczenia jednego z równań poprzez wprowadzenie nowej zmiennej. Nowe równanie rozwiązuje się dla wprowadzonej niewiadomej, a otrzymaną wartość wykorzystuje się do wyznaczenia pierwotnej zmiennej.

Przykład pokazuje, że wprowadzając nową zmienną t, możliwe było sprowadzenie pierwszego równania układu do standardowego trójmianu kwadratowego. Wielomian można rozwiązać, znajdując dyskryminator.

Wartość dyskryminatora należy znaleźć ze znanego wzoru: D = b2 - 4*a*c, gdzie D jest pożądanym wyróżnikiem, b, a, c są współczynnikami wielomianu. W podanym przykładzie a=1, b=16, c=39, zatem D=100. Jeśli dyskryminator jest większy od zera, to są dwa rozwiązania: t = -b±√D / 2*a, jeśli dyskryminator jest mniejszy od zera, to jest jedno rozwiązanie: x = -b / 2*a.

Rozwiązanie dla powstałych układów można znaleźć metodą addycji.

Wizualna metoda rozwiązywania układów

Nadaje się do 3 układów równań. Metoda polega na konstruowaniu wykresów każdego równania wchodzącego w skład układu na osi współrzędnych. Współrzędne punktów przecięcia krzywych będą rozwiązaniem ogólnym układu.

Metoda graficzna ma wiele niuansów. Przyjrzyjmy się kilku przykładom rozwiązywania układów równań liniowych w sposób wizualny.

Jak widać na przykładzie, dla każdej prostej skonstruowano dwa punkty, arbitralnie wybrano wartości zmiennej x: 0 i 3. Na podstawie wartości x znaleziono wartości dla y: 3 i 0. Na wykresie zaznaczono punkty o współrzędnych (0, 3) i (3, 0) i połączono je linią.

Kroki należy powtórzyć dla drugiego równania. Punkt przecięcia prostych jest rozwiązaniem układu.

Poniższy przykład wymaga znalezienia graficznego rozwiązania układu równań liniowych: 0,5x-y+2=0 i 0,5x-y-1=0.

Jak widać na przykładzie układ nie ma rozwiązania, ponieważ wykresy są równoległe i nie przecinają się na całej długości.

Układy z przykładów 2 i 3 są podobne, ale po zbudowaniu staje się oczywiste, że ich rozwiązania są różne. Należy pamiętać, że nie zawsze można stwierdzić, czy układ ma rozwiązanie, czy nie, zawsze konieczne jest skonstruowanie wykresu.

Macierz i jej odmiany

Macierze służą do zwięzłego pisania układu równań liniowych. Macierz to specjalny rodzaj tabeli wypełnionej liczbami. n*m ma n - wierszy i m - kolumn.

Macierz jest kwadratowa, gdy liczba kolumn i wierszy jest równa. Macierz-wektor jest macierzą jednokolumnową z nieskończenie możliwą liczbą wierszy. Macierz z jedynkami wzdłuż jednej z przekątnych i innymi elementami zerowymi nazywa się tożsamością.

Macierz odwrotna to macierz, przez którą po pomnożeniu pierwotna zamienia się w macierz jednostkową; taka macierz istnieje tylko dla pierwotnej kwadratowej.

Zasady przekształcania układu równań w macierz

W odniesieniu do układów równań współczynniki i wyrazy wolne równań zapisuje się jako liczby macierzowe; jedno równanie to jeden wiersz macierzy.

Mówi się, że wiersz macierzy jest niezerowy, jeśli przynajmniej jeden element wiersza jest różny od zera. Dlatego jeśli w którymkolwiek z równań liczba zmiennych jest różna, wówczas w miejsce brakującej niewiadomej należy wpisać zero.

Kolumny macierzy muszą ściśle odpowiadać zmiennym. Oznacza to, że współczynniki zmiennej x można zapisać tylko w jednej kolumnie, np. w pierwszej, współczynnik nieznanej y - tylko w drugiej.

Podczas mnożenia macierzy wszystkie elementy macierzy są kolejno mnożone przez liczbę.

Opcje znajdowania macierzy odwrotnej

Wzór na znalezienie macierzy odwrotnej jest dość prosty: K -1 = 1 / |K|, gdzie K -1 jest macierzą odwrotną, a |K| jest wyznacznikiem macierzy. |K| nie może być równe zero, wówczas układ ma rozwiązanie.

Wyznacznik można łatwo obliczyć dla macierzy dwa na dwa, wystarczy pomnożyć elementy przekątne przez siebie. Dla opcji „trzy na trzy” istnieje wzór |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + za 3 b 2 do 1 . Możesz skorzystać ze wzoru lub pamiętać, że musisz wziąć po jednym elemencie z każdego wiersza i każdej kolumny, aby w pracy nie powtarzały się numery kolumn i rzędów elementów.

Rozwiązywanie przykładów układów równań liniowych metodą macierzową

Macierzowa metoda znajdowania rozwiązania pozwala na ograniczenie uciążliwych wpisów przy rozwiązywaniu układów z dużą liczbą zmiennych i równań.

W przykładzie a nm to współczynniki równań, macierz to wektor. x n to zmienne, a b n to terminy wolne.

Rozwiązywanie układów metodą Gaussa

W matematyce wyższej metodę Gaussa bada się łącznie z metodą Cramera, a proces znajdowania rozwiązań układów nazywa się metodą rozwiązań Gaussa-Cramera. Metody te służą do znajdowania zmiennych układów o dużej liczbie równań liniowych.

Metoda Gaussa jest bardzo podobna do rozwiązań metodą podstawienia i dodawania algebraicznego, ale jest bardziej systematyczna. Na zajęciach szkolnych stosuje się rozwiązanie metodą Gaussa dla układów 3 i 4 równań. Celem metody jest sprowadzenie układu do postaci odwróconego trapezu. Za pomocą przekształceń algebraicznych i podstawień wartość jednej zmiennej znajduje się w jednym z równań układu. Drugie równanie jest wyrażeniem z 2 niewiadomymi, natomiast 3 i 4 z 3 i 4 zmiennymi.

Po doprowadzeniu układu do opisanej postaci dalsze rozwiązanie sprowadza się do sekwencyjnego podstawienia znanych zmiennych do równań układu.

W podręcznikach szkolnych dla klasy 7 przykład rozwiązania metodą Gaussa opisano w następujący sposób:

Jak widać na przykładzie, w kroku (3) otrzymano dwa równania: 3x 3 -2x 4 =11 i 3x 3 +2x 4 =7. Rozwiązanie któregokolwiek z równań pozwoli ci znaleźć jedną ze zmiennych x n.

Twierdzenie 5, o którym mowa w tekście, stwierdza, że ​​jeśli jedno z równań układu zostanie zastąpione równaniem równoważnym, wówczas powstały układ będzie również równoważny pierwotnemu.

Metoda Gaussa jest trudna do zrozumienia dla gimnazjalistów, ale jest jednym z najciekawszych sposobów rozwijania pomysłowości dzieci zapisanych do zaawansowanych programów nauczania na lekcjach matematyki i fizyki.

Aby ułatwić rejestrację, obliczenia zwykle wykonuje się w następujący sposób:

Współczynniki równań i wyrazy wolne zapisuje się w postaci macierzy, gdzie każdemu wierszowi macierzy odpowiada jedno z równań układu. oddziela lewą stronę równania od prawej. Cyfry rzymskie wskazują numery równań w układzie.

Najpierw zapisz macierz, z którą będziesz pracować, a następnie wszystkie czynności wykonane z jednym z wierszy. Otrzymaną macierz zapisuje się po znaku „strzałki” i kontynuuje niezbędne działania algebraiczne aż do uzyskania wyniku.

Wynikiem powinna być macierz, w której jedna z przekątnych jest równa 1, a wszystkie pozostałe współczynniki są równe zeru, to znaczy macierz jest zredukowana do postaci jednostkowej. Nie możemy zapomnieć o wykonaniu obliczeń z liczbami po obu stronach równania.

Ta metoda zapisywania jest mniej uciążliwa i pozwala nie rozpraszać się wypisywaniem wielu niewiadomych.

Swobodne korzystanie z dowolnej metody rozwiązania będzie wymagało ostrożności i pewnego doświadczenia. Nie wszystkie metody mają charakter stosowany. Niektóre metody znajdowania rozwiązań są bardziej preferowane w określonym obszarze działalności człowieka, inne służą celom edukacyjnym.

Układ m równań liniowych z n niewiadomymi zwany systemem formy

Gdzie ij I b ja (I=1,…,M; B=1,…,N) to kilka znanych liczb, i x 1 ,…,x n- nieznany. W wyznaczaniu współczynników ij pierwszy indeks I oznacza numer równania, a drugi J– liczba niewiadomych, przy której stoi ten współczynnik.

Współczynniki niewiadomych zapiszemy w postaci macierzy , który nazwiemy macierz układu.

Liczby po prawej stronie równań to b 1 ,…,b m są nazywane wolni członkowie.

Całość N liczby c 1 ,…,c n zwany decyzja danego układu, jeżeli każde równanie układu staje się równością po podstawieniu do niego liczb c 1 ,…,c n zamiast odpowiednich niewiadomych x 1 ,…,x n.

Naszym zadaniem będzie znalezienie rozwiązań dla systemu. W takim przypadku mogą zaistnieć trzy sytuacje:

Układ równań liniowych, który ma co najmniej jedno rozwiązanie nazywa się wspólny. W przeciwnym razie, tj. jeśli system nie ma rozwiązań, nazywa się go nie wspólne.

Zastanówmy się, jak znaleźć rozwiązania dla systemu.

METODA MATRYCOWA ROZWIĄZANIA UKŁADÓW RÓWNAŃ LINIOWYCH

Macierze umożliwiają krótkie zapisanie układu równań liniowych. Niech będzie dany układ 3 równań z trzema niewiadomymi:

Rozważmy macierz systemu i macierze kolumny nieznanych i wolnych terminów

Znajdźmy pracę

te. w wyniku iloczynu otrzymujemy lewe strony równań tego układu. Następnie korzystając z definicji równości macierzy układ ten można zapisać w postaci

lub krócej A∙X=B.

Oto macierze A I B są znane, oraz macierz X nieznany. Trzeba go znaleźć, bo... jego elementy są rozwiązaniem tego systemu. To równanie nazywa się równanie macierzowe.

Niech wyznacznik macierzy będzie różny od zera | A| ≠ 0. Następnie równanie macierzowe rozwiązuje się w następujący sposób. Pomnóż obie strony równania po lewej stronie przez macierz A-1, odwrotność macierzy A: . Ponieważ A -1 A = E I mi∙X = X, wówczas otrzymujemy rozwiązanie równania macierzowego w postaci X = A -1 B .

Należy zauważyć, że ponieważ macierz odwrotną można znaleźć tylko dla macierzy kwadratowych, metoda macierzowa może rozwiązać tylko te układy, w których liczba równań pokrywa się z liczbą niewiadomych. Jednakże macierzowy zapis układu jest możliwy również w przypadku, gdy liczba równań nie jest równa liczbie niewiadomych, wówczas macierz A nie będzie kwadratowy i dlatego nie da się znaleźć rozwiązania układu w postaci X = A -1 B.

Przykłady. Rozwiązywać układy równań.

REGUŁA CRAMERA

Rozważmy układ 3 równań liniowych z trzema niewiadomymi:

Wyznacznik trzeciego rzędu odpowiadający macierzy układu, tj. złożony ze współczynników niewiadomych,

zwany wyznacznik systemu.

Skomponujmy jeszcze trzy wyznaczniki w następujący sposób: zamień kolejno 1, 2 i 3 kolumny w wyznaczniku D na kolumnę wolnych terminów

Następnie możemy udowodnić następujący wynik.

Twierdzenie (reguła Cramera). Jeżeli wyznacznik układu Δ ≠ 0, to rozpatrywany układ ma jedno i tylko jedno rozwiązanie, a

Dowód. Rozważmy więc układ trzech równań z trzema niewiadomymi. Pomnóżmy pierwsze równanie układu przez dopełnienie algebraiczne 11 element 11, 2 równanie – włączone 21 i 3. – dalej 31:

Dodajmy te równania:

Przyjrzyjmy się każdemu z nawiasów i prawej stronie tego równania. Według twierdzenia o rozwinięciu wyznacznika w elementach pierwszej kolumny

Podobnie można wykazać, że i .

Wreszcie łatwo to zauważyć

Otrzymujemy zatem równość: .

Stąd, .

Równości i wyprowadza się w podobny sposób, z czego wynika stwierdzenie twierdzenia.

Zauważamy zatem, że jeśli wyznacznik układu Δ ≠ 0, to układ ma rozwiązanie jednoznaczne i odwrotnie. Jeżeli wyznacznik układu jest równy zero, to układ albo ma nieskończoną liczbę rozwiązań, albo nie ma rozwiązań, tj. niekompatybilny.

Przykłady. Rozwiązać układ równań

METODA GAUssa

Omówione wcześniej metody można zastosować do rozwiązania tylko tych układów, w których liczba równań pokrywa się z liczbą niewiadomych, a wyznacznik układu musi być różny od zera. Metoda Gaussa jest bardziej uniwersalna i odpowiednia dla układów o dowolnej liczbie równań. Polega ona na konsekwentnym eliminowaniu niewiadomych z równań układu.

Rozważmy ponownie układ trzech równań z trzema niewiadomymi:

.

Pierwsze równanie pozostawimy bez zmian, a z drugiego i trzeciego wykluczymy terminy zawierające x 1. Aby to zrobić, podziel drugie równanie przez A 21 i pomnóż przez – A 11, a następnie dodaj go do pierwszego równania. Podobnie dzielimy trzecie równanie przez A 31 i pomnóż przez – A 11, a następnie dodaj go do pierwszego. W efekcie oryginalny system przyjmie postać:

Teraz z ostatniego równania eliminujemy termin zawierający x 2. Aby to zrobić, podziel trzecie równanie przez, pomnóż przez drugie i dodaj z drugim. Wtedy będziemy mieli układ równań:

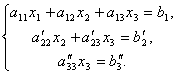
Stąd z ostatniego równania łatwo jest znaleźć x 3, to z drugiego równania x 2 i wreszcie, od 1-go - x 1.

W przypadku stosowania metody Gaussa równania można w razie potrzeby zamienić.

Często zamiast pisać nowy układ równań ograniczają się do napisania rozszerzonej macierzy układu:

a następnie doprowadź go do postaci trójkątnej lub ukośnej za pomocą elementarnych przekształceń.

DO elementarne przemiany macierze obejmują następujące przekształcenia:

1. przestawianie wierszy lub kolumn;
2. mnożenie ciągu przez liczbę inną niż zero;
3. dodanie innych linii do jednej linii.

Przykłady: Rozwiązywać układy równań metodą Gaussa.

Zatem układ ma nieskończoną liczbę rozwiązań.