Maksymalna wartość własna macierzy. Równanie charakterystyczne macierzy

Macierze diagonalne mają najprostszą strukturę. Powstaje pytanie, czy można znaleźć bazę, w której macierz operatora liniowego miałaby postać diagonalną. Taka podstawa istnieje.
Dana jest nam przestrzeń liniowa R n i działający w niej operator liniowy A; w tym przypadku operator A bierze w siebie R n, czyli A:R n → R n .

Definicja. Niezerowy wektor nazywany jest wektorem własnym operatora A, jeśli operator A przekłada się na wektor współliniowy. Liczba λ nazywana jest wartością własną lub wartością własną operatora A, odpowiadającą wektorowi własnemu.
Zwróćmy uwagę na niektóre właściwości wartości własnych i wektorów własnych.
1. Dowolna kombinacja liniowa wektorów własnych operator A odpowiadający tej samej wartości własnej λ jest wektorem własnym o tej samej wartości własnej.
2. Wektory własne operator A z parami różnymi wartościami własnymi λ 1 , λ 2 , …, λ m są liniowo niezależne.
3. Jeśli wartości własne λ 1 = λ 2 = λ m = λ, to wartość własna λ odpowiada nie więcej niż m liniowo niezależnym wektorom własnym.

Zatem, jeśli istnieje n liniowo niezależnych wektorów własnych , odpowiadające różnym wartościom własnym λ 1, λ 2, ..., λ n, wówczas są one liniowo niezależne, dlatego można je przyjąć jako podstawę przestrzeni R n. Znajdźmy postać macierzy operatora liniowego A na podstawie jego wektorów własnych, dla których będziemy działać z operatorem A na podstawie wektorów bazowych: Następnie .
Zatem macierz operatora liniowego A na podstawie jego wektorów własnych ma postać diagonalną, a wartości własne operatora A są wzdłuż przekątnej.
Czy istnieje inna baza, w której macierz ma postać diagonalną? Odpowiedź na to pytanie daje następujące twierdzenie.

Twierdzenie. Macierz operatora liniowego A w bazie (i = 1..n) ma postać diagonalną wtedy i tylko wtedy, gdy wszystkie wektory bazy są wektorami własnymi operatora A.

Zasada znajdowania wartości własnych i wektorów własnych

. (*)

(1)
Gdzie - macierz operatora liniowego.

Układ (1) ma rozwiązanie niezerowe, jeśli jego wyznacznik D jest równy zero

Przykład 12. Operator liniowy A działa w R 3 zgodnie z prawem, gdzie x 1, x 2, .., x n są współrzędnymi wektora w bazie , , . Znajdź wartości własne i wektory własne tego operatora.
Rozwiązanie. Budujemy macierz tego operatora:
.
Tworzymy układ wyznaczania współrzędnych wektorów własnych:

Tworzymy równanie charakterystyczne i rozwiązujemy je:

.
λ 1,2 = -1, λ 3 = 3.
Podstawiając λ = -1 do układu, mamy:
Lub
Ponieważ , to istnieją dwie zmienne zależne i jedna zmienna wolna.
Niech zatem x 1 będzie wolną niewiadomą Rozwiązujemy ten układ w dowolny sposób i znajdujemy rozwiązanie ogólne tego układu: Podstawowy układ rozwiązań składa się z jednego rozwiązania, ponieważ n - r = 3 - 2 = 1.
Zbiór wektorów własnych odpowiadających wartości własnej λ = -1 ma postać: , gdzie x 1 jest dowolną liczbą różną od zera. Wybierzmy jeden wektor z tego zbioru, na przykład stawiając x 1 = 1: .
Rozumując podobnie, znajdujemy wektor własny odpowiadający wartości własnej λ = 3: .
W przestrzeni R 3 baza składa się z trzech liniowo niezależnych wektorów, ale otrzymaliśmy tylko dwa liniowo niezależne wektory własne, z których nie można złożyć bazy w R 3. W konsekwencji nie możemy sprowadzić macierzy A operatora liniowego do postaci diagonalnej.

Przykład 13. Biorąc pod uwagę macierz .
1. Udowodnić, że wektor jest wektorem własnym macierzy A. Znajdź wartość własną odpowiadającą temu wektorowi własnemu.
2. Znajdź bazę, w której macierz A ma postać diagonalną.
Rozwiązanie.
1. Jeśli , to jest wektorem własnym

.
Wektor (1, 8, -1) jest wektorem własnym. Wartość własna λ = -1.
Macierz ma postać diagonalną w bazie składającej się z wektorów własnych. Jeden z nich jest sławny. Znajdźmy resztę.
Szukamy wektorów własnych z układu:

Równanie charakterystyczne: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Znajdźmy wektor własny odpowiadający wartości własnej λ = -3:

Rząd macierzy tego układu wynosi dwa i jest równy liczbie niewiadomych, więc ten układ ma tylko rozwiązanie zerowe x 1 = x 3 = 0. x 2 tutaj może być dowolną wartością różną od zera, na przykład x 2 = 1. Zatem wektor (0,1,0) jest wektorem własnym odpowiadającym λ = -3. Sprawdźmy:
.
Jeżeli λ = 1, wówczas otrzymujemy układ
Ranga macierzy wynosi dwa. Przekreślamy ostatnie równanie.
Niech x 3 będzie wolną niewiadomą. Wtedy x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Zakładając x 3 = 1, mamy (-3,-9,1) - wektor własny odpowiadający wartości własnej λ = 1. Sprawdź:

.
Ponieważ wartości własne są rzeczywiste i odrębne, odpowiadające im wektory są liniowo niezależne, więc można je przyjąć za podstawę w R 3 . Zatem w podstawie , , macierz A ma postać:
.
Nie każdą macierz operatora liniowego A:R n → R n można sprowadzić do postaci diagonalnej, ponieważ dla niektórych operatorów liniowych może istnieć mniej niż n liniowych niezależnych wektorów własnych. Jeśli jednak macierz jest symetryczna, to pierwiastek charakterystycznego równania krotności m odpowiada dokładnie m liniowo niezależnym wektorom.

Definicja. Macierz symetryczna to macierz kwadratowa, w której elementy symetryczne względem głównej przekątnej są równe, czyli w której .
Notatki. 1. Wszystkie wartości własne macierzy symetrycznej są rzeczywiste.
2. Wektory własne macierzy symetrycznej odpowiadające param różnym wartościom własnym są ortogonalne.
Jako jedno z wielu zastosowań badanej aparatury rozważamy problem określenia typu krzywej drugiego rzędu.

Definicja 9.3. Wektor X zwany wektor własny matryce A, jeśli istnieje taka liczba λ, że zachodzi równość: A X= λ X, to znaczy wynik zastosowania do X transformacja liniowa określona przez macierz A, jest pomnożeniem tego wektora przez liczbę λ . Sam numer λ zwany wartość własna matryce A.

Podstawianie we wzorach (9.3) x` jot = λx jot, otrzymujemy układ równań do wyznaczania współrzędnych wektora własnego:

. (9.5)

Ten liniowy układ jednorodny będzie miał nietrywialne rozwiązanie tylko wtedy, gdy jego główną wyznacznikiem będzie 0 (reguła Cramera). Zapisując ten warunek w postaci:

otrzymujemy równanie do wyznaczania wartości własnych λ , zwany równanie charakterystyczne. W skrócie można to przedstawić następująco:

| A - λE | = 0, (9.6)

ponieważ jego lewa strona zawiera wyznacznik macierzy A-λE. Względny wielomian λ | A - λE| zwany charakterystyczny wielomian macierze A.

Własności charakterystycznego wielomianu:

1) Charakterystyczny wielomian transformacji liniowej nie zależy od wyboru podstawy. Dowód. (patrz (9.4)), ale stąd, . Zatem nie zależy to od wyboru podstawy. Oznacza to, że | A-λE| nie zmienia się po przejściu na nową podstawę.

2) Jeżeli macierz A transformacja liniowa jest symetryczny(te. i ij = a ji), wówczas wszystkie pierwiastki równania charakterystycznego (9.6) są liczbami rzeczywistymi.

Właściwości wartości własnych i wektorów własnych:

1) Jeśli wybierzesz bazę z wektorów własnych x 1, x 2, x 3 , odpowiadające wartościom własnym λ 1, λ 2, λ 3 matryce A, to na tej podstawie transformacja liniowa A ma macierz w postaci diagonalnej:

(9.7) Dowód tej własności wynika z definicji wektorów własnych.

2) Jeśli wartości własne transformacji A są różne, to odpowiadające im wektory własne są liniowo niezależne.

3) Jeśli charakterystyczny wielomian macierzy A ma trzy różne pierwiastki, to w pewnym sensie macierz A ma wygląd diagonalny.

Znajdźmy wartości własne i wektory własne macierzy. Stwórzmy równanie charakterystyczne: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ł - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Znajdźmy współrzędne wektorów własnych odpowiadających każdej znalezionej wartości λ. Z (9.5) wynika, że ​​jeśli X (1) ={x 1, x 2, x 3) – odpowiedni wektor własny λ 1 = -2, zatem

- system współpracujący, ale niepewny. Jego rozwiązanie można zapisać w postaci X (1) ={A,0,-A), gdzie a jest dowolną liczbą. W szczególności, jeśli tego wymagamy | X (1) |=1, X (1) =

Podstawianie do układu (9.5) λ 2 =3 otrzymujemy układ wyznaczania współrzędnych drugiego wektora własnego - X (2) ={1, 2, 3}:

, Gdzie X (2) ={b, -b,b) lub, pod warunkiem | X (2) |=1, X (2) =

Dla λ 3 = 6 znajdź wektor własny X (3) ={z 1 , z 2 , z 3}:

, X (3) ={C,2c, ok) lub w wersji znormalizowanej

x (3) = Można to zauważyć X (1) X (2) = ab-ab= 0, X (1) X (3) = ac-ac= 0, X (2) X (3) = pne- 2p.n.e. + p.n.e= 0. Zatem wektory własne tej macierzy są parami ortogonalne.

Wykład 10.

Formy kwadratowe i ich powiązanie z macierzami symetrycznymi. Właściwości wektorów własnych i wartości własnych macierzy symetrycznej. Sprowadzanie postaci kwadratowej do postaci kanonicznej.

Definicja 10.1.Kwadratowy kształt rzeczywiste zmienne x 1, x 2,…, x n nazywa się w tych zmiennych wielomianem drugiego stopnia, który nie zawiera wyrazu wolnego i wyrazów pierwszego stopnia.

Przykłady form kwadratowych:

(N = 2),

(N = 3). (10.1)

Przypomnijmy definicję macierzy symetrycznej podaną na ostatnim wykładzie:

Definicja 10.2. Nazywa się macierz kwadratową symetryczny, jeśli , to znaczy, jeśli elementy macierzy symetryczne względem głównej przekątnej są równe.

Właściwości wartości własnych i wektorów własnych macierzy symetrycznej:

1) Wszystkie wartości własne macierzy symetrycznej są rzeczywiste.

Dowód (dla N = 2).

Niech matryca A ma postać: . Utwórzmy równanie charakterystyczne:

(10.2) Znajdźmy dyskryminator:

Dlatego równanie ma tylko pierwiastki rzeczywiste.

2) Wektory własne macierzy symetrycznej są ortogonalne.

Dowód (dla N= 2).

Współrzędne wektorów własnych i muszą spełniać równania.

UKŁAD JEDNORODNYCH RÓWNAŃ LINIOWYCH

Układ jednorodnych równań liniowych jest układem postaci

To oczywiste, że w tym przypadku , ponieważ wszystkie elementy jednej z kolumn tych wyznaczników są równe zero.

Ponieważ niewiadome znajdują się zgodnie ze wzorami , to w przypadku, gdy Δ ≠ 0, układ ma jednoznaczne rozwiązanie zerowe X = y = z= 0. Jednak w przypadku wielu problemów interesującym pytaniem jest to, czy układ jednorodny ma rozwiązania inne niż zero.

Twierdzenie. Aby układ liniowych równań jednorodnych miał rozwiązanie niezerowe, konieczne i wystarczające jest, aby Δ ≠ 0.

Jeśli więc wyznacznik Δ ≠ 0, to układ ma rozwiązanie jednoznaczne. Jeśli Δ ≠ 0, to układ liniowych równań jednorodnych ma nieskończoną liczbę rozwiązań.

Przykłady.

Wektory własne i wartości własne macierzy

Niech będzie dana macierz kwadratowa , X– jakaś macierz-kolumna, której wysokość pokrywa się z rzędem macierzy A. .

W wielu problemach musimy wziąć pod uwagę równanie X

gdzie λ jest pewną liczbą. Oczywiste jest, że dla dowolnego λ równanie to ma rozwiązanie zerowe.

Nazywa się liczbę λ, dla której to równanie ma niezerowe rozwiązania wartość własna matryce A, A X dla takiego λ nazywa się wektor własny matryce A.

Znajdźmy wektor własny macierzy A. Ponieważ mi∙X = X, wówczas równanie macierzowe można przepisać jako Lub . W rozszerzonej formie równanie to można przepisać jako układ równań liniowych. Naprawdę .

I dlatego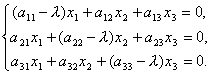

Otrzymaliśmy w ten sposób układ jednorodnych równań liniowych do wyznaczania współrzędnych x 1, x 2, x 3 wektor X. Aby układ miał rozwiązania niezerowe konieczne i wystarczające jest, aby wyznacznik układu był równy zeru, tj.

Jest to równanie trzeciego stopnia dla λ. To jest nazwane równanie charakterystyczne matryce A i służy do określenia wartości własnych λ.

Każda wartość własna λ odpowiada wektorowi własnemu X, którego współrzędne wyznaczane są z układu przy odpowiedniej wartości λ.

Przykłady.

ALGEBRA WEKTOROWA. KONCEPCJA WEKTORA

Studiując różne gałęzie fizyki, istnieją wielkości, które są całkowicie określone poprzez określenie ich wartości liczbowych, na przykład długości, powierzchni, masy, temperatury itp. Wielkości takie nazywane są skalarami. Jednak oprócz nich istnieją również wielkości, dla których, oprócz wartości liczbowej, konieczna jest znajomość ich kierunku w przestrzeni, np. siły działającej na ciało, prędkości i przyspieszenia ciała. ciało poruszające się w przestrzeni, natężenie pola magnetycznego w danym punkcie przestrzeni itp. Wielkości takie nazywane są wielkościami wektorowymi.

Wprowadźmy ścisłą definicję.

Odcinek reżyserowany Nazwijmy odcinek, po którego końcach wiadomo, który z nich jest pierwszy, a który drugi.

Wektor nazywany segmentem skierowanym mającym określoną długość, tj. Jest to odcinek o określonej długości, w którym jeden z ograniczających go punktów przyjmuje się za początek, a drugi za koniec. Jeśli A– początek wektora, B jest jego końcem, wówczas wektor oznacza się symbolem, ponadto wektor często oznacza się pojedynczą literą. Na rysunku wektor jest oznaczony segmentem, a jego kierunek strzałką.

Moduł Lub długość Wektor nazywa się długością skierowanego odcinka, który go definiuje. Oznaczone przez || lub ||.

Jako wektory uwzględnimy także tzw. wektor zerowy, którego początek i koniec pokrywają się. Jest wyznaczony. Wektor zerowy nie ma określonego kierunku, a jego moduł wynosi zero ||=0.

Nazywa się wektory współliniowy, jeżeli znajdują się na tej samej linii lub na liniach równoległych. Co więcej, jeśli wektory i są w tym samym kierunku, napiszemy , przeciwnie.

Nazywa się wektory położone na liniach prostych równoległych do tej samej płaszczyzny współpłaszczyznowy.

Nazywa się te dwa wektory równy, jeśli są współliniowe, mają ten sam kierunek i są równej długości. W tym wypadku piszą.

Z definicji równości wektorów wynika, że ​​wektor może być transportowany równolegle do siebie, umieszczając swój początek w dowolnym punkcie przestrzeni.

Na przykład.

DZIAŁANIA LINIOWE NA WEKTORACH

1. Mnożenie wektora przez liczbę.

   Iloczyn wektora i liczby λ jest nowym wektorem takim, że:

   Iloczyn wektora i liczby λ jest oznaczony przez .

   

   Na przykład, istnieje wektor skierowany w tym samym kierunku co wektor i mający długość o połowę krótszą od wektora.

   Wprowadzona operacja ma następującą postać nieruchomości:

2. Dodatek wektorowy.

   Niech i będą dwoma dowolnymi wektorami. Weźmy dowolny punkt O i skonstruuj wektor. Potem od rzeczy A odłóżmy wektor na bok. Nazywa się wektor łączący początek pierwszego wektora z końcem drugiego kwota tych wektorów i jest oznaczone .

   

   Sformułowana definicja dodawania wektorów nazywa się reguła równoległoboku, ponieważ tę samą sumę wektorów można otrzymać w następujący sposób. Odłóżmy od tematu O wektory i . Zbudujmy równoległobok na tych wektorach OABC. Skoro wektory, to wektor, który jest przekątną równoległoboku narysowanego od wierzchołka O, będzie oczywiście sumą wektorów.

   

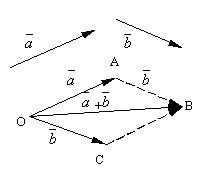
   Łatwo jest sprawdzić poniższe właściwości dodawania wektorów.

3. Różnica wektorowa.

   Nazywa się wektor współliniowy z danym wektorem, równy długości i przeciwnie skierowany naprzeciwko wektor dla wektora i jest oznaczony przez . Przeciwny wektor można uznać za wynik pomnożenia wektora przez liczbę λ = –1: .

Wektor własny macierzy kwadratowej to taki, który pomnożony przez daną macierz daje wektor współliniowy. Krótko mówiąc, gdy macierz jest mnożona przez wektor własny, ten ostatni pozostaje taki sam, ale pomnożony przez określoną liczbę.

Definicja

Wektor własny jest niezerowym wektorem V, który pomnożony przez macierz kwadratową M sam zostaje powiększony o pewną liczbę λ. W notacji algebraicznej wygląda to następująco:

M × V = λ × V,

gdzie λ jest wartością własną macierzy M.

Spójrzmy na przykład numeryczny. Dla ułatwienia zapisu liczby w macierzy będą oddzielone średnikiem. Miejmy macierz:

• M = 0; 4;
• 6; 10.

Pomnóżmy to przez wektor kolumnowy:

• V = -2;

Kiedy mnożymy macierz przez wektor kolumnowy, otrzymujemy również wektor kolumnowy. W ścisłym języku matematycznym wzór na pomnożenie macierzy 2 × 2 przez wektor kolumnowy będzie wyglądał następująco:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 oznacza element macierzy M znajdujący się w pierwszym rzędzie i pierwszej kolumnie, a M22 oznacza element znajdujący się w drugim rzędzie i drugiej kolumnie. Dla naszej macierzy elementy te są równe M11 = 0, M12 = 4, M21 = 6, M22 10. Dla wektora kolumnowego wartości te są równe V11 = –2, V21 = 1. Zgodnie z tym wzorem otrzymujemy następujący wynik iloczynu macierzy kwadratowej przez wektor:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Dla wygody napiszmy wektor kolumnowy w wierszu. Zatem pomnożyliśmy macierz kwadratową przez wektor (-2; 1), w wyniku czego otrzymaliśmy wektor (4; -2). Oczywiście jest to ten sam wektor pomnożony przez λ = -2. Lambda w tym przypadku oznacza wartość własną macierzy.

Wektor własny macierzy jest wektorem współliniowym, czyli obiektem, który nie zmienia swojego położenia w przestrzeni po pomnożeniu przez macierz. Pojęcie kolinearności w algebrze wektorowej jest podobne do pojęcia równoległości w geometrii. W interpretacji geometrycznej wektory współliniowe są równoległymi odcinkami o różnych długościach. Od czasów Euklidesa wiemy, że na jedną prostą przypada nieskończona liczba prostych równoległych do niej, zatem logiczne jest założenie, że każda macierz ma nieskończoną liczbę wektorów własnych.

Z poprzedniego przykładu jasno wynika, że ​​wektorami własnymi mogą być (-8; 4), (16; -8) i (32, -16). Są to wszystkie wektory współliniowe odpowiadające wartości własnej λ = -2. Mnożąc pierwotną macierz przez te wektory, nadal otrzymamy wektor różniący się od oryginału 2 razy. Dlatego przy rozwiązywaniu problemów znalezienia wektora własnego konieczne jest znalezienie tylko liniowo niezależnych obiektów wektorowych. Najczęściej dla macierzy n × n istnieje n wektorów własnych. Nasz kalkulator jest przeznaczony do analizy macierzy kwadratowych drugiego rzędu, więc prawie zawsze w wyniku zostaną znalezione dwa wektory własne, za wyjątkiem przypadków, gdy się pokrywają.

W powyższym przykładzie znaliśmy z góry wektor własny oryginalnej macierzy i jasno określiliśmy liczbę lambda. Jednak w praktyce wszystko dzieje się na odwrót: najpierw znajdują się wartości własne, a dopiero potem wektory własne.

Algorytm rozwiązania

Spójrzmy jeszcze raz na pierwotną macierz M i spróbujmy znaleźć oba jej wektory własne. Zatem macierz wygląda następująco:

• M = 0; 4;
• 6; 10.

Najpierw należy wyznaczyć wartość własną λ, co wymaga obliczenia wyznacznika macierzy:

• (0 - λ); 4;
• 6; (10 - λ).

Macierz tę uzyskuje się odejmując niewiadomą λ od elementów na głównej przekątnej. Wyznacznik wyznacza się za pomocą standardowego wzoru:

• detA = M11 × M21 – M12 × M22
• detA = (0 – λ) × (10 – λ) – 24

Ponieważ nasz wektor musi być różny od zera, przyjmujemy otrzymane równanie jako liniowo zależne i przyrównujemy naszą wyznacznik detA do zera.

(0 - λ) × (10 - λ) - 24 = 0

Otwórzmy nawiasy i uzyskajmy równanie charakterystyczne macierzy:

λ 2 - 10 λ - 24 = 0

Jest to standardowe równanie kwadratowe, które należy rozwiązać za pomocą dyskryminatora.

re = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

Pierwiastkiem dyskryminatora jest sqrt(D) = 14, zatem λ1 = -2, λ2 = 12. Teraz dla każdej wartości lambda musimy znaleźć wektor własny. Wyraźmy współczynniki systemowe dla λ = -2.

• M - λ × mi = 2; 4;
• 6; 12.

W tym wzorze E jest macierzą tożsamości. Na podstawie otrzymanej macierzy tworzymy układ równań liniowych:

2x + 4 lata = 6x + 12 lat,

gdzie x i y są elementami wektorów własnych.

Zbierzmy wszystkie X po lewej stronie i wszystkie Y po prawej. Oczywiście - 4x = 8 lat. Podziel wyrażenie przez - 4 i otrzymaj x = –2y. Teraz możemy wyznaczyć pierwszy wektor własny macierzy, przyjmując dowolne wartości niewiadomych (pamiętajmy o nieskończoności wektorów własnych liniowo zależnych). Weźmy y = 1, następnie x = –2. Dlatego pierwszy wektor własny wygląda jak V1 = (–2; 1). Wróć na początek artykułu. To właśnie ten obiekt wektorowy pomnożyliśmy macierz, aby zademonstrować koncepcję wektora własnego.

Znajdźmy teraz wektor własny dla λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Stwórzmy ten sam układ równań liniowych;

• -12x + 4 lata = 6x - 2 lata
• -18x = -6 lat
• 3x = y.

Teraz bierzemy x = 1, zatem y = 3. Zatem drugi wektor własny wygląda jak V2 = (1; 3). Mnożąc pierwotną macierz przez zadany wektor, otrzymamy zawsze ten sam wektor pomnożony przez 12. Na tym kończy się algorytm rozwiązania. Teraz wiesz, jak ręcznie wyznaczyć wektor własny macierzy.

• wyznacznik;
• ślad, czyli suma elementów na głównej przekątnej;
• ranga, czyli maksymalna liczba liniowo niezależnych wierszy/kolumn.

Program działa według powyższego algorytmu, maksymalnie skracając proces rozwiązywania. Warto zaznaczyć, że w programie lambda oznaczona jest literą „c”. Spójrzmy na przykład numeryczny.

Przykład działania programu

Spróbujmy wyznaczyć wektory własne dla następującej macierzy:

• M = 5; 13;
• 4; 14.

Wprowadźmy te wartości do komórek kalkulatora i uzyskajmy odpowiedź w następującej formie:

• Ranga matrycy: 2;
• Wyznacznik macierzy: 18;
• Ślad matrycy: 19;
• Obliczanie wektora własnego: c 2 − 19,00c + 18,00 (równanie charakterystyczne);
• Obliczenie wektora własnego: 18 (pierwsza wartość lambda);
• Obliczenie wektora własnego: 1 (druga wartość lambda);
• Układ równań dla wektora 1: -13x1 + 13y1 = 4x1 − 4y1;
• Układ równań dla wektora 2: 4x1 + 13y1 = 4x1 + 13y1;
• Wektor własny 1: (1; 1);
• Wektor własny 2: (-3,25; 1).

W ten sposób otrzymaliśmy dwa liniowo niezależne wektory własne.

Wniosek

Algebra liniowa i geometria analityczna to standardowe przedmioty na każdym kierunku inżynierii pierwszego roku. Duża liczba wektorów i macierzy jest przerażająca, a przy tak uciążliwych obliczeniach łatwo jest popełnić błąd. Nasz program pozwoli studentom sprawdzić swoje obliczenia lub automatycznie rozwiązać problem znalezienia wektora własnego. W naszym katalogu znajdziesz inne kalkulatory algebry liniowej, wykorzystaj je na studiach lub w pracy.

www.strona pozwala znaleźć. Witryna wykonuje obliczenia. W ciągu kilku sekund serwer poda prawidłowe rozwiązanie. Równanie charakterystyczne macierzy będzie wyrażeniem algebraicznym znalezionym przy użyciu reguły obliczania wyznacznika matryce matryce, natomiast wzdłuż głównej przekątnej wystąpią różnice w wartościach elementów diagonalnych i zmiennej. Podczas obliczania równanie charakterystyczne macierzy online, każdy element matryce zostanie pomnożona przez odpowiednie inne elementy matryce. Znajdź w trybie online możliwe tylko dla kwadratu matryce. Znalezienie operacji równanie charakterystyczne macierzy online sprowadza się do obliczenia sumy algebraicznej iloczynu pierwiastków matryce w wyniku znalezienia wyznacznika matryce, jedynie w celu ustalenia równanie charakterystyczne macierzy online. Operacja ta zajmuje w teorii szczególne miejsce matryce, pozwala znaleźć wartości własne i wektory za pomocą pierwiastków. Zadanie znalezienia równanie charakterystyczne macierzy online składa się z mnożenia elementów matryce następnie sumowanie tych produktów według określonej reguły. www.strona znajdzie równanie charakterystyczne macierzy dany wymiar w trybie online. Obliczenie równanie charakterystyczne macierzy online biorąc pod uwagę jego wymiar, jest to znalezienie wielomianu o współczynnikach liczbowych lub symbolicznych, znalezionych zgodnie z regułą obliczania wyznacznika matryce- jako suma iloczynów odpowiednich elementów matryce, jedynie w celu ustalenia równanie charakterystyczne macierzy online. Znajdowanie wielomianu ze względu na zmienną dla kwadratu matryce, jako definicja równanie charakterystyczne macierzy, powszechne w teorii matryce. Znaczenie pierwiastków wielomianu równanie charakterystyczne macierzy online służy do wyznaczania wektorów własnych i wartości własnych dla matryce. Co więcej, jeśli wyznacznik matryce będzie wtedy równa zeru równanie charakterystyczne macierzy będzie nadal istnieć, w przeciwieństwie do sytuacji odwrotnej matryce. Aby obliczyć równanie charakterystyczne macierzy lub znajdź kilka na raz równania charakterystyczne macierzy, musisz poświęcić dużo czasu i wysiłku, a nasz serwer znajdzie to w ciągu kilku sekund równanie charakterystyczne macierzy online. W tym przypadku odpowiedź na znalezienie równanie charakterystyczne macierzy online będzie poprawny i z wystarczającą dokładnością, nawet jeśli liczby zostaną znalezione równanie charakterystyczne macierzy online będzie irracjonalne. Na stronie www.strona W elementach dozwolone są wpisy znakowe matryce, to jest równanie charakterystyczne macierzy online można przedstawić w ogólnej formie symbolicznej podczas obliczeń równanie charakterystyczne macierzy online. Przy rozwiązywaniu problemu znalezienia warto sprawdzić otrzymaną odpowiedź równanie charakterystyczne macierzy online korzystanie z witryny www.strona. Podczas wykonywania operacji obliczania wielomianu - równanie charakterystyczne macierzy, przy rozwiązywaniu tego problemu należy zachować ostrożność i szczególną koncentrację. Z kolei nasza strona pomoże Ci sprawdzić decyzję w danym temacie równanie charakterystyczne macierzy online. Jeśli nie masz czasu na długie sprawdzanie rozwiązanych problemów, to www.strona z pewnością będzie wygodnym narzędziem do sprawdzania przy znajdowaniu i obliczaniu równanie charakterystyczne macierzy online.