The maximum eigenvalue of a matrix. Matrix characteristic equation

Diagonal-type matrices are most simply arranged. The question arises whether it is possible to find a basis in which the matrix of a linear operator would have a diagonal form. Such a basis exists.
Let a linear space R n and a linear operator A acting in it be given; in this case, the operator A takes R n into itself, that is, A:R n → R n .

Definition. A non-zero vector is called an eigenvector of the operator A if the operator A translates into a vector collinear to it, that is, . The number λ is called the eigenvalue or eigenvalue of the operator A corresponding to the eigenvector .
We note some properties of eigenvalues ​​and eigenvectors.
1. Any linear combination of eigenvectors of the operator A corresponding to the same eigenvalue λ is an eigenvector with the same eigenvalue.
2. Eigenvectors operator A with pairwise distinct eigenvalues ​​λ 1 , λ 2 , …, λ m are linearly independent.
3. If the eigenvalues ​​λ 1 =λ 2 = λ m = λ, then the eigenvalue λ corresponds to no more than m linearly independent eigenvectors.

So, if there are n linearly independent eigenvectors corresponding to different eigenvalues ​​λ 1 , λ 2 , …, λ n , then they are linearly independent, therefore, they can be taken as the basis of the space R n . Let us find the form of the matrix of the linear operator A in the basis of its eigenvectors, for which we act with the operator A on the basis vectors: then .
Thus, the matrix of the linear operator A in the basis of its eigenvectors has a diagonal form, and the eigenvalues ​​of the operator A are on the diagonal.
Is there another basis in which the matrix has a diagonal form? The answer to this question is given by the following theorem.

Theorem. The matrix of a linear operator A in the basis (i = 1..n) has a diagonal form if and only if all vectors of the basis are eigenvectors of the operator A.

Rule for finding eigenvalues ​​and eigenvectors

. (*)

(1)
where is the matrix of the linear operator.

System (1) has a nonzero solution if its determinant D is equal to zero

Example 12. The linear operator A acts in R 3 according to the law , where x 1 , x 2 , .., x n are the coordinates of the vector in the basis , , . Find the eigenvalues ​​and eigenvectors of this operator.
Decision. We build the matrix of this operator:
.
We compose a system for determining the coordinates of eigenvectors:

We compose the characteristic equation and solve it:

.
λ 1,2 = -1, λ 3 = 3.
Substituting λ = -1 into the system, we have:
or
As , then there are two dependent variables and one free variable.
Let x 1 be a free unknown, then We solve this system in any way and find the general solution of this system: The fundamental system of solutions consists of one solution, since n - r = 3 - 2 = 1.
The set of eigenvectors corresponding to the eigenvalue λ = -1 has the form: , where x 1 is any number other than zero. Let's choose one vector from this set, for example, by setting x 1 = 1: .
Arguing similarly, we find the eigenvector corresponding to the eigenvalue λ = 3: .
In the space R 3 the basis consists of three linearly independent vectors, but we have obtained only two linearly independent eigenvectors, from which the basis in R 3 cannot be formed. Consequently, the matrix A of a linear operator cannot be reduced to a diagonal form.

Example 13 Given a matrix .
1. Prove that the vector is an eigenvector of matrix A. Find the eigenvalue corresponding to this eigenvector.
2. Find a basis in which the matrix A has a diagonal form.
Decision.
1. If , then is an eigenvector

.
Vector (1, 8, -1) is an eigenvector. Eigenvalue λ = -1.
The matrix has a diagonal form in the basis consisting of eigenvectors. One of them is famous. Let's find the rest.
We are looking for eigenvectors from the system:

Characteristic equation: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Find the eigenvector corresponding to the eigenvalue λ = -3:

The rank of the matrix of this system is equal to two and is equal to the number of unknowns, therefore this system has only a zero solution x 1 = x 3 = 0. x 2 here can be anything other than zero, for example, x 2 = 1. Thus, the vector (0 ,1,0) is an eigenvector corresponding to λ = -3. Let's check:
.
If λ = 1, then we get the system
The rank of the matrix is ​​two. Cross out the last equation.
Let x 3 be the free unknown. Then x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Assuming x 3 = 1, we have (-3,-9,1) - an eigenvector corresponding to the eigenvalue λ = 1. Check:

.
Since the eigenvalues ​​are real and different, the vectors corresponding to them are linearly independent, so they can be taken as a basis in R 3 . Thus, in the basis , , matrix A has the form:
.
Not every matrix of a linear operator A:R n → R n can be reduced to a diagonal form, since for some linear operators there may be less than n linearly independent eigenvectors. However, if the matrix is ​​symmetric, then exactly m linearly independent vectors correspond to the root of the characteristic equation of multiplicity m.

Definition. A symmetric matrix is ​​a square matrix in which the elements that are symmetric with respect to the main diagonal are equal, that is, in which .
Remarks. 1. All eigenvalues ​​of a symmetric matrix are real.
2. Eigenvectors of a symmetric matrix corresponding to pairwise different eigenvalues ​​are orthogonal.
As one of the numerous applications of the studied apparatus, we consider the problem of determining the form of a second-order curve.

Definition 9.3. Vector X called own vector matrices BUT if there is such a number λ, that the equality holds: BUT X= λ X, that is, the result of applying to X linear transformation given by the matrix BUT, is the multiplication of this vector by the number λ . The number itself λ called own number matrices BUT.

Substituting into formulas (9.3) x` j = λx j , we obtain a system of equations for determining the coordinates of the eigenvector:

. (9.5)

This linear homogeneous system will have a non-trivial solution only if its main determinant is 0 (Cramer's rule). By writing this condition in the form:

we get an equation for determining the eigenvalues λ called characteristic equation. Briefly, it can be represented as follows:

| A-λE | = 0, (9.6)

since its left side is the determinant of the matrix A-λE. Polynomial with respect to λ | A-λE| called characteristic polynomial matrices a.

Properties of the characteristic polynomial:

1) The characteristic polynomial of a linear transformation does not depend on the choice of the basis. Proof. (see (9.4)), but hence, . Thus, does not depend on the choice of basis. Hence, and | A-λE| does not change upon transition to a new basis.

2) If the matrix BUT linear transformation is symmetrical(those. a ij = a ji), then all the roots of the characteristic equation (9.6) are real numbers.

Properties of eigenvalues ​​and eigenvectors:

1) If we choose a basis from eigenvectors x 1, x 2, x 3 corresponding to the eigenvalues λ 1 , λ 2 , λ 3 matrices BUT, then in this basis the linear transformation A has a diagonal matrix:

(9.7) The proof of this property follows from the definition of eigenvectors.

2) If the transformation eigenvalues BUT are different, then the eigenvectors corresponding to them are linearly independent.

3) If the characteristic polynomial of the matrix BUT has three different roots, then in some basis the matrix BUT has a diagonal shape.

Let's find the eigenvalues ​​and eigenvectors of the matrix Let's make the characteristic equation: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Find the coordinates of the eigenvectors corresponding to each found value λ. From (9.5) it follows that if X (1) ={x 1 , x 2 , x 3) is the eigenvector corresponding to λ 1 = -2, then

is a collaborative but indeterminate system. Its solution can be written as X (1) ={a,0,-a), where a is any number. In particular, if you require that | x (1) |=1, X (1) =

Substituting into the system (9.5) λ 2 =3, we get a system for determining the coordinates of the second eigenvector - x (2) ={y1,y2,y3}:

, where X (2) ={b,-b,b) or, provided | x (2) |=1, x (2) =

For λ 3 = 6 find the eigenvector x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) or in the normalized version

x (3) = It can be seen that X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = bc- 2bc + bc= 0. Thus, the eigenvectors of this matrix are pairwise orthogonal.

Lecture 10

Quadratic forms and their connection with symmetric matrices. Properties of eigenvectors and eigenvalues ​​of a symmetric matrix. Reduction of a quadratic form to a canonical form.

Definition 10.1.quadratic form real variables x 1, x 2,…, x n a polynomial of the second degree with respect to these variables is called, which does not contain a free term and terms of the first degree.

Examples of quadratic forms:

(n = 2),

(n = 3). (10.1)

Recall the definition of a symmetric matrix given in the last lecture:

Definition 10.2. The square matrix is ​​called symmetrical, if , that is, if the matrix elements symmetric with respect to the main diagonal are equal.

Properties of eigenvalues ​​and eigenvectors of a symmetric matrix:

1) All eigenvalues ​​of a symmetric matrix are real.

Proof (for n = 2).

Let the matrix BUT looks like: . Let's make the characteristic equation:

(10.2) Find the discriminant:

Therefore, the equation has only real roots.

2) The eigenvectors of a symmetric matrix are orthogonal.

Proof (for n= 2).

The coordinates of the eigenvectors and must satisfy the equations.

SYSTEM OF HOMOGENEOUS LINEAR EQUATIONS

A system of homogeneous linear equations is a system of the form

It is clear that in this case , because all elements of one of the columns in these determinants are equal to zero.

Since the unknowns are found by the formulas , then in the case when Δ ≠ 0, the system has a unique zero solution x = y = z= 0. However, in many problems the question of whether a homogeneous system has solutions other than zero is of interest.

Theorem. For a system of linear homogeneous equations to have a nonzero solution, it is necessary and sufficient that Δ ≠ 0.

So, if the determinant is Δ ≠ 0, then the system has a unique solution. If Δ ≠ 0, then the system of linear homogeneous equations has an infinite number of solutions.

Examples.

Eigenvectors and Matrix Eigenvalues

Let a square matrix be given , X is some matrix-column whose height coincides with the order of the matrix A. .

In many problems, one has to consider the equation for X

where λ is some number. It is clear that for any λ this equation has a zero solution .

The number λ for which this equation has nonzero solutions is called eigenvalue matrices A, a X for such λ is called own vector matrices A.

Let's find the eigenvector of the matrix A. Insofar as E∙X=X, then the matrix equation can be rewritten as or . In expanded form, this equation can be rewritten as a system of linear equations. Really .

And therefore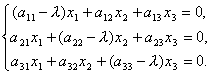

So, we got a system of homogeneous linear equations for determining the coordinates x 1, x2, x 3 vector X. For the system to have non-zero solutions, it is necessary and sufficient that the determinant of the system be equal to zero, i.e.

This is a 3rd degree equation with respect to λ. It's called characteristic equation matrices A and serves to determine the eigenvalues ​​λ.

Each eigenvalue λ corresponds to an eigenvector X, whose coordinates are determined from the system at the corresponding value of λ.

Examples.

VECTOR ALGEBRA. VECTOR CONCEPT

When studying various branches of physics, there are quantities that are completely determined by setting their numerical values, for example, length, area, mass, temperature, etc. Such values ​​are called scalar. However, in addition to them, there are also quantities, for the determination of which, in addition to the numerical value, it is also necessary to know their direction in space, for example, the force acting on the body, the speed and acceleration of the body when it moves in space, the magnetic field strength at a given point in space and etc. Such quantities are called vector quantities.

Let us introduce a rigorous definition.

Directional segment Let's call a segment, relative to the ends of which it is known which of them is the first and which is the second.

Vector a directed segment is called, having a certain length, i.e. This is a segment of a certain length, in which one of the points limiting it is taken as the beginning, and the second - as the end. If a A is the beginning of the vector, B is its end, then the vector is denoted by the symbol, in addition, the vector is often denoted by a single letter . In the figure, the vector is indicated by a segment, and its direction by an arrow.

module or long vector is called the length of the directed segment that defines it. Denoted by || or ||.

The so-called zero vector, whose beginning and end coincide, will also be referred to as vectors. It is marked. The zero vector has no definite direction and its modulus is equal to zero ||=0.

Vectors and are called collinear if they are located on the same line or on parallel lines. In this case, if the vectors and are equally directed, we will write , oppositely.

Vectors located on straight lines parallel to the same plane are called coplanar.

Two vectors and are called equal if they are collinear, have the same direction, and are equal in length. In this case, write .

It follows from the definition of equality of vectors that a vector can be moved parallel to itself by placing its origin at any point in space.

for example.

LINEAR OPERATIONS ON VECTORS

1. Multiplying a vector by a number.

   The product of a vector by a number λ is a new vector such that:

   The product of a vector and a number λ is denoted by .

   

   For example, is a vector pointing in the same direction as the vector and having a length half that of the vector .

   The entered operation has the following properties:

2. Addition of vectors.

   Let and be two arbitrary vectors. Take an arbitrary point O and construct a vector . After that, from the point A set aside the vector . The vector connecting the beginning of the first vector with the end of the second is called sum of these vectors and is denoted .

   

   The formulated definition of vector addition is called parallelogram rule, since the same sum of vectors can be obtained as follows. Set aside from the point O vectors and . Construct a parallelogram on these vectors OABC. Since the vectors , then the vector , which is the diagonal of the parallelogram drawn from the vertex O, will obviously be the sum of vectors .

   

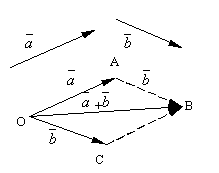
   It is easy to check the following vector addition properties.

3. Difference of vectors.

   A vector collinear to a given vector , equal in length and oppositely directed, is called opposite vector for a vector and is denoted by . The opposite vector can be considered as the result of vector multiplication by the number λ = –1: .

An eigenvector of a square matrix is ​​one that, when multiplied by a given matrix, results in a collinear vector. In simple words, when a matrix is ​​multiplied by an eigenvector, the latter remains the same, but multiplied by some number.

Definition

An eigenvector is a non-zero vector V, which, when multiplied by a square matrix M, becomes itself, increased by some number λ. In algebraic notation, this looks like:

M × V = λ × V,

where λ is an eigenvalue of the matrix M.

Let's consider a numerical example. For convenience of writing, the numbers in the matrix will be separated by a semicolon. Let's say we have a matrix:

• M = 0; 4;
• 6; 10.

Let's multiply it by a column vector:

• V = -2;

When multiplying a matrix by a column vector, we also get a column vector. In strict mathematical language, the formula for multiplying a 2 × 2 matrix by a column vector would look like this:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 means the element of the matrix M, standing in the first row and first column, and M22 is the element located in the second row and second column. For our matrix, these elements are M11 = 0, M12 = 4, M21 = 6, M22 10. For a column vector, these values ​​are V11 = –2, V21 = 1. According to this formula, we get the following result of the product of a square matrix by a vector:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

For convenience, we write the column vector into a row. So, we have multiplied the square matrix by the vector (-2; 1), resulting in the vector (4; -2). Obviously, this is the same vector multiplied by λ = -2. Lambda in this case denotes an eigenvalue of the matrix.

An eigenvector of a matrix is ​​a collinear vector, that is, an object that does not change its position in space when it is multiplied by a matrix. The concept of collinearity in vector algebra is similar to the term of parallelism in geometry. In geometric interpretation, collinear vectors are parallel directed segments of different lengths. Since the time of Euclid, we know that a single line has an infinite number of lines parallel to it, so it is logical to assume that each matrix has an infinite number of eigenvectors.

From the previous example, it can be seen that both (-8; 4), and (16; -8), and (32, -16) can be eigenvectors. All these are collinear vectors corresponding to the eigenvalue λ = -2. When multiplying the original matrix by these vectors, we will still get a vector as a result, which differs from the original by 2 times. That is why, when solving problems for finding an eigenvector, it is required to find only linearly independent vector objects. Most often, for an n × n matrix, there are n-th number of eigenvectors. Our calculator is designed for the analysis of second-order square matrices, so almost always two eigenvectors will be found as a result, except when they coincide.

In the example above, we knew in advance the eigenvector of the original matrix and visually determined the lambda number. However, in practice, everything happens the other way around: at the beginning there are eigenvalues ​​and only then eigenvectors.

Solution algorithm

Let's look at the original matrix M again and try to find both of its eigenvectors. So the matrix looks like:

• M = 0; 4;
• 6; 10.

To begin with, we need to determine the eigenvalue λ, for which we need to calculate the determinant of the following matrix:

• (0 − λ); 4;
• 6; (10 − λ).

This matrix is ​​obtained by subtracting the unknown λ from the elements on the main diagonal. The determinant is determined by the standard formula:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Since our vector must not be zero, we take the resulting equation as linearly dependent and equate our determinant detA to zero.

(0 − λ) × (10 − λ) − 24 = 0

Let's open the brackets and get the characteristic equation of the matrix:

λ 2 − 10λ − 24 = 0

This is a standard quadratic equation that needs to be solved in terms of the discriminant.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

The root of the discriminant is sqrt(D) = 14, so λ1 = -2, λ2 = 12. Now for each lambda value, we need to find an eigenvector. Let us express the coefficients of the system for λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

In this formula, E is the identity matrix. Based on the obtained matrix, we compose a system of linear equations:

2x + 4y = 6x + 12y

where x and y are elements of the eigenvector.

Let's collect all the X's on the left and all the Y's on the right. Obviously - 4x = 8y. Divide the expression by - 4 and get x = -2y. Now we can determine the first eigenvector of the matrix by taking any values ​​of the unknowns (remember about the infinity of linearly dependent eigenvectors). Let's take y = 1, then x = -2. Therefore, the first eigenvector looks like V1 = (–2; 1). Return to the beginning of the article. It was this vector object that we multiplied the matrix by to demonstrate the concept of an eigenvector.

Now let's find the eigenvector for λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Let us compose the same system of linear equations;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x=y.

Now let's take x = 1, hence y = 3. Thus, the second eigenvector looks like V2 = (1; 3). When multiplying the original matrix by this vector, the result will always be the same vector multiplied by 12. This completes the solution algorithm. Now you know how to manually define an eigenvector of a matrix.

• determinant;
• trace, that is, the sum of the elements on the main diagonal;
• rank, i.e. the maximum number of linearly independent rows/columns.

The program operates according to the above algorithm, minimizing the solution process. It is important to point out that in the program the lambda is denoted by the letter "c". Let's look at a numerical example.

Program example

Let's try to define eigenvectors for the following matrix:

• M=5; thirteen;
• 4; 14.

Let's enter these values ​​into the cells of the calculator and get the answer in the following form:

• Matrix rank: 2;
• Matrix determinant: 18;
• Matrix trace: 19;
• Eigenvector calculation: c 2 − 19.00c + 18.00 (characteristic equation);
• Eigenvector calculation: 18 (first lambda value);
• Eigenvector calculation: 1 (second lambda value);
• System of equations of vector 1: -13x1 + 13y1 = 4x1 − 4y1;
• Vector 2 equation system: 4x1 + 13y1 = 4x1 + 13y1;
• Eigenvector 1: (1; 1);
• Eigenvector 2: (-3.25; 1).

Thus, we have obtained two linearly independent eigenvectors.

Conclusion

Linear algebra and analytic geometry are standard subjects for any freshman in engineering. A large number of vectors and matrices is terrifying, and it is easy to make a mistake in such cumbersome calculations. Our program will allow students to check their calculations or automatically solve the problem of finding an eigenvector. There are other linear algebra calculators in our catalog, use them in your study or work.

www.site allows you to find . The site does the calculation. In a few seconds, the server will give the correct solution. The characteristic equation for the matrix will be an algebraic expression found by the rule for calculating the determinant matrices matrices, while on the main diagonal there will be differences in the values ​​of the diagonal elements and the variable. When calculating characteristic equation for matrix online, each element matrices will be multiplied with the corresponding other elements matrices. Find in mode online possible only for square matrices. Find operation characteristic equation for matrix online reduces to calculating the algebraic sum of the product of elements matrices as a result of finding the determinant matrices, only for the purpose of determining characteristic equation for matrix online. This operation occupies a special place in the theory matrices, allows you to find eigenvalues ​​and vectors using roots . Finding task characteristic equation for matrix online is to multiply elements matrices with the subsequent summation of these products according to a certain rule. www.site finds characteristic equation for matrix given dimension in the mode online. calculation characteristic equation for matrix online for a given dimension, this is finding a polynomial with numerical or symbolic coefficients found by the rule for calculating the determinant matrices- as the sum of the products of the corresponding elements matrices, only for the purpose of determining characteristic equation for matrix online. Finding a polynomial with respect to a variable for a square matrices, as definition characteristic equation for the matrix, common in theory matrices. The value of the roots of the polynomial characteristic equation for matrix online used to define eigenvectors and eigenvalues ​​for matrices. However, if the determinant matrices will be zero, then matrix characteristic equation will still exist, unlike the reverse matrices. In order to calculate characteristic equation for matrix or search for several at once matrices characteristic equations, you need to spend a lot of time and effort, while our server will find characteristic equation for online matrix. In this case, the answer by finding characteristic equation for matrix online will be correct and with sufficient accuracy, even if the numbers when finding characteristic equation for matrix online will be irrational. Online www.site character entries are allowed in elements matrices, i.e characteristic equation for online matrix can be represented in a general symbolic form when calculating characteristic equation matrix online. It is useful to check the answer obtained when solving the problem of finding characteristic equation for matrix online using the site www.site. When performing the operation of calculating a polynomial - characteristic equation of the matrix, it is necessary to be attentive and extremely concentrated in solving this problem. In turn, our site will help you check your decision on the topic characteristic equation matrix online. If you do not have time for long checks of solved problems, then www.site will certainly be a convenient tool for checking when finding and calculating characteristic equation for matrix online.