Најдете ги сопствените вредности на операторот. Сопствени вредности (броеви) и сопствени вектори Примери на решенија

Матриците од дијагонален тип се наједноставно подредени. Се поставува прашањето дали е можно да се најде основа во која матрицата на линеарен оператор би имала дијагонална форма. Таква основа постои.
Нека се дадени линеарен простор R n и линеарен оператор A што дејствува во него; во овој случај, операторот A го зема R n во себе, односно A:R n → R n .

Дефиниција. Ненулта вектор се нарекува сопствен вектор на операторот A ако операторот A се преточи во вектор колинеарен на него, односно. Бројот λ се нарекува сопствена вредност или сопствена вредност на операторот A што одговара на сопствениот вектор.
Забележуваме некои својства на сопствени вредности и сопствени вектори.
1. Секоја линеарна комбинација на сопствени вектори на операторот A што одговара на истата сопствена вредност λ е сопствен вектор со иста сопствена вредност.
2. Сопствени вектори операторот А со парови различни сопствени вредности λ 1 , λ 2 , ..., λ m се линеарно независни.
3. Ако сопствените вредности λ 1 =λ 2 = λ m = λ, тогаш сопствената вредност λ одговара на не повеќе од m линеарно независни сопствени вектори.

Значи, ако има n линеарно независни сопствени вектори што одговараат на различни сопствени вредности λ 1 , λ 2 , ..., λ n , тогаш тие се линеарно независни, затоа, може да се земат како основа на просторот R n . Да ја најдеме формата на матрицата на линеарниот оператор А врз основа на неговите сопствени вектори, за кои дејствуваме со операторот A врз основа на вектори: тогаш .
Така, матрицата на линеарниот оператор А во основата на неговите сопствени вектори има дијагонална форма, а сопствените вредности на операторот А се на дијагоналата.
Дали постои друга основа во која матрицата има дијагонална форма? Одговорот на ова прашање го дава следната теорема.

Теорема. Матрицата на линеарен оператор А во основата (i = 1..n) има дијагонална форма ако и само ако сите вектори на основата се сопствени вектори на операторот А.

Правило за наоѓање сопствени вредности и сопствени вектори

. (*)

(1)
каде е матрицата на линеарниот оператор.

Системот (1) има ненула решение ако неговата детерминанта D е еднаква на нула

Пример 12. Линеарниот оператор A дејствува во R 3 според законот , каде што x 1 , x 2 , .., x n се координатите на векторот во основата , , . Најдете ги сопствените вредности и сопствени вектори на овој оператор.
Решение. Ја градиме матрицата на овој оператор:
.
Составуваме систем за одредување на координатите на сопствени вектори:

Ја составуваме карактеристичната равенка и ја решаваме:

.
λ 1,2 = -1, λ 3 = 3.
Заменувајќи го λ = -1 во системот, имаме:
или
Бидејќи , тогаш има две зависни променливи и една слободна променлива.
Нека x 1 е слободна непозната, тогаш Овој систем го решаваме на кој било начин и го наоѓаме општото решение на овој систем: Основниот систем на решенија се состои од едно решение, бидејќи n - r = 3 - 2 = 1.
Множеството сопствени вектори што одговараат на сопствената вредност λ = -1 има форма: , каде што x 1 е кој било број различен од нула. Ајде да избереме еден вектор од ова множество, на пример, со поставување x 1 = 1: .
Аргументирајќи слично, го наоѓаме сопствениот вектор што одговара на сопствената вредност λ = 3: .
Во просторот R 3 основата се состои од три линеарно независни вектори, но добивме само два линеарно независни сопствени вектори, од кои не може да се формира основата во R 3. Следствено, матрицата А на линеарен оператор не може да се сведе на дијагонална форма.

Пример 13 Дадена е матрица .
1. Докажи дека векторот е сопствен вектор на матрицата A. Најдете ја сопствената вредност што одговара на овој сопствен вектор.
2. Најдете основа во која матрицата А има дијагонална форма.
Решение.
1. Ако , тогаш е сопствен вектор

.
Векторот (1, 8, -1) е сопствен вектор. Сопствена вредност λ = -1.
Матрицата има дијагонална форма во основата која се состои од сопствени вектори. Еден од нив е познат. Ајде да го најдеме остатокот.
Бараме сопствени вектори од системот:

Карактеристична равенка: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Најдете го сопствениот вектор што одговара на сопствената вредност λ = -3:

Рангот на матрицата на овој систем е еднаков на два и е еднаков на бројот на непознати, затоа овој систем има само нула решение x 1 = x 3 = 0. x 2 овде може да биде нешто друго освен нула, на пример, x 2 = 1. Така, векторот (0 ,1,0) е сопствен вектор што одговара на λ = -3. Ајде да провериме:
.
Ако λ = 1, тогаш го добиваме системот
Рангот на матрицата е два. Пречкртајте ја последната равенка.
Нека x 3 е слободната непозната. Потоа x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Претпоставувајќи x 3 = 1, имаме (-3,-9,1) - сопствен вектор што одговара на сопствената вредност λ = 1. Проверете:

.
Бидејќи сопствените вредности се реални и различни, векторите што одговараат на нив се линеарно независни, така што тие можат да се земат како основа во R3. Така, во основата , , матрицата А има форма:
.
Не секоја матрица на линеарен оператор A:R n → R n може да се сведе на дијагонална форма, бидејќи за некои линеарни оператори може да има помалку од n линеарно независни сопствени вектори. Меѓутоа, ако матрицата е симетрична, тогаш точно m линеарно независни вектори одговараат на коренот на карактеристичната равенка на мноштвото m.

Дефиниција. Симетрична матрица е квадратна матрица во која елементите кои се симетрични во однос на главната дијагонала се еднакви, односно во која .
Забелешки. 1. Сите сопствени вредности на симетрична матрица се реални.
2. Сопствени вектори на симетрична матрица што одговараат на пар различни сопствени вредности се ортогонални.
Како една од бројните примени на испитуваниот апарат, го разгледуваме проблемот на определување на формата на крива од втор ред.

Сопствени вредности (броеви) и сопствени вектори.
Примери за решенија

Биди свој

Од двете равенки произлегува дека .

Ајде да ставиме тогаш: .

Како резултат: е вториот сопствен вектор.

Да ги повториме важните точки:

– добиениот систем секако има општо решение (равенките се линеарно зависни);

- „Y“ се избира така што е цел број, а првата координата „x“ е цел број, позитивна и што е можно помала.

– проверуваме дали конкретното решение ја задоволува секоја равенка на системот.

Одговори .

Средните „контролни точки“ беа сосема доволни, така што проверката на еднаквостите, во принцип, е излишна.

Во различни извори на информации, координатите на сопствени вектори често се пишуваат не во колони, туку во редови, на пример: (и, да бидам искрен, и јас ги пишував во редови). Оваа опција е прифатлива, но во светлината на темата линеарни трансформациитехнички поудобно за употреба вектори на колони.

Можеби решението ви се чинеше многу долго, но тоа е само затоа што го коментирав првиот пример многу детално.

Пример 2

матрици

Тренираме сами! Приближен примерок од конечниот дизајн на задачата на крајот од лекцијата.

Понекогаш треба да извршите дополнителна задача, имено:

напишете го канонското разложување на матрицата

Што е тоа?

Ако се формираат матричните сопствени вектори основа, тогаш може да се претстави како:

Каде е матрица составена од координати на сопствени вектори, - дијагоналаматрица со соодветни сопствени вредности.

Ова распаѓање на матрицата се нарекува канонскиили дијагонала.

Размислете за матрицата од првиот пример. Нејзини сопствени вектори линеарно независни(неколинеарни) и формираат основа. Ајде да направиме матрица од нивните координати:

На главна дијагоналаматрици по редСе наоѓаат сопствените вредности, а останатите елементи се еднакви на нула:
- уште еднаш ја нагласувам важноста на редот: „два“ одговара на 1-виот вектор и затоа се наоѓа во 1-ва колона, „три“ - на 2-ри вектор.

Според вообичаениот алгоритам за пронаоѓање инверзна матрицаили Гаус-Јордан методнајдете . Не, тоа не е печатна грешка! - пред вас е редок настан, како затемнување на Сонцето, кога обратното се совпадна со оригиналната матрица.

Останува да се напише канонското распаѓање на матрицата:

Системот може да се реши со помош на елементарни трансформации и во следните примери ќе прибегнеме кон овој метод. Но, овде методот „училиште“ работи многу побрзо. Од 3-та равенка изразуваме: - замени во втората равенка:

Бидејќи првата координата е нула, добиваме систем, од секоја равенка на која следи дека .

И повторно обрнете внимание на задолжителното присуство на линеарна врска. Ако се добие само тривијално решение , тогаш или сопствената вредност е пронајдена погрешно, или системот е компајлиран/решен со грешка.

Компактните координати даваат вредност

Својствектор:

И уште еднаш проверуваме дали е пронајденото решение ја задоволува секоја равенка на системот. Во следните параграфи и во следните задачи, препорачувам оваа желба да се прифати како задолжително правило.

2) За сопствената вредност, следејќи го истиот принцип, го добиваме следниов систем:

Од 2-та равенка на системот изразуваме: - замена во третата равенка:

Бидејќи координатата „Z“ е еднаква на нула, добиваме систем, од секоја равенка од која следи линеарна зависност.

Нека

Проверуваме дали решението ја задоволува секоја равенка на системот.

Така, сопствениот вектор: .

3) И, конечно, системот одговара на неговата сопствена вредност:

Втората равенка изгледа наједноставна, затоа ја изразуваме од неа и ја заменуваме во 1-та и 3-та равенка:

Сè е во ред - беше откриена линеарна зависност, која ја заменуваме во изразот:

Како резултат на тоа, „X“ и „Y“ беа изразени преку „Z“: . Во пракса, не е неопходно да се постигнат само такви односи; во некои случаи е попогодно да се изразат и преку или и преку . Или дури и „воз“ - на пример, „X“ преку „Y“ и „Y“ преку „Z“

Ајде да ставиме тогаш:

Проверуваме дали е пронајденото решение ја задоволува секоја равенка на системот и напишете го третиот сопствен вектор

Одговори: сопствени вектори:

Геометриски, овие вектори дефинираат три различни просторни насоки („Таму и повторно назад“), според кој линеарна трансформацијаги трансформира ненулта вектори (сопствени вектори) во вектори колинеарни на нив.

Ако по услов беше потребно да се најде канонско проширување на , тогаш ова е можно овде, бидејќи различни сопствени вредности одговараат на различни линеарно независни сопствени вектори. Ние правиме матрица од нивните координати, дијагоналната матрица од релевантнисопствени вредности и најдете инверзна матрица .

Ако според условот е потребно да се напише матрица на линеарна трансформација во основа на сопствени вектори, потоа одговорот го даваме во форма . Има разлика, и значајна разлика!За оваа матрица е матрицата „де“.

Проблем со поедноставни пресметки за независно решение:

Пример 5

Најдете сопствени вектори на линеарна трансформација дадени со матрица

Кога наоѓате сопствени броеви, обидете се да не го доведете случајот до полином од 3 степен. Покрај тоа, вашите системски решенија може да се разликуваат од моите решенија - тука нема недвосмисленост; и векторите што ќе ги најдете може да се разликуваат од примероците на вектори до пропорционалност на нивните соодветни координати. На пример, и. Естетички е попријатно да се претстави одговорот во форма на , но во ред е ако застанете на втората опција. Сепак, постојат разумни граници за сè, верзијата веќе не изгледа многу добро.

Приближен конечен примерок од задачата на крајот од лекцијата.

Како да се реши проблемот во случај на повеќе сопствени вредности?

Општиот алгоритам останува ист, но има свои особености и препорачливо е некои делови од решението да се задржат во поригорозен академски стил:

Пример 6

Најдете сопствени вредности и сопствени вектори

Решение

Се разбира, да ја искористиме прекрасната прва колона:

И, по факторингирање на квадратниот трином:

Како резултат на тоа, се добиваат сопствени вредности, од кои две се повеќекратни.

Ајде да ги најдеме сопствените вектори:

1) Ќе се справиме со осамен војник според „поедноставена“ шема:

Од последните две равенки, јасно е видлива еднаквоста, која, очигледно, треба да се замени во првата равенка на системот:

Нема подобра комбинација:
Својствектор:

2-3) Сега отстрануваме неколку стражари. Во овој случај, тоа може да биде или два или еденсопствен вектор. Без разлика на мноштвото на корените, вредноста ја заменуваме во детерминантата , што ни го носи следново хомоген систем на линеарни равенки:

Сопствени вектори се токму векторите
фундаментален систем на одлучување

Всушност, во текот на целата лекција се занимававме само со наоѓање на векторите на основниот систем. Засега овој термин не беше особено потребен. Патем, оние умешни студенти кои во камуфлажа хомогени равенки, ќе биде принуден да го пуши сега.

Единственото дејство беше да се отстранат дополнителните линии. Резултатот е матрица „еден по три“ со формален „чекор“ во средината.
– основна променлива, – слободни променливи. Постојат две слободни променливи, така постојат и два вектори на основниот систем.

Да ја изразиме основната променлива во однос на слободните променливи: . Нултиот фактор пред „x“ му овозможува да преземе апсолутно какви било вредности (што е јасно видливо и од системот на равенки).

Во контекст на овој проблем, попогодно е да се напише општото решение не во ред, туку во колона:

Парот одговара на сопствен вектор:
Парот одговара на сопствен вектор:

Забелешка : софистицираните читатели можат да ги подигнат овие вектори усно - само со анализа на системот , но тука е потребно одредено знаење: има три променливи, ранг на системска матрица- единица значи фундаментален систем на одлучувањесе состои од 3 – 1 = 2 вектори. Сепак, пронајдените вектори се совршено видливи дури и без ова знаење, чисто на интуитивно ниво. Во овој случај, третиот вектор ќе биде напишан уште „поубаво“: . Сепак, ве предупредувам, во друг пример можеби нема едноставна селекција, поради што резервацијата е наменета за искусни луѓе. Освен тоа, зошто да не се земе како трет вектор, да речеме, ? На крајот на краиштата, неговите координати исто така ја задоволуваат секоја равенка на системот и векторите се линеарно независни. Оваа опција, во принцип, е погодна, но „крива“, бидејќи „другиот“ вектор е линеарна комбинација на вектори на основниот систем.

Одговори: сопствени вредности: , сопствени вектори:

Сличен пример за решение „направи сам“:

Пример 7

Најдете сопствени вредности и сопствени вектори

Приближен примерок за завршување на крајот од лекцијата.

Треба да се забележи дека и во 6-от и во 7-от пример, се добива тројка линеарно независни сопствени вектори, и затоа оригиналната матрица може да биде претставена во канонската експанзија. Но, таквите малини не се случуваат во сите случаи:

Пример 8

Решение: состави и реши ја карактеристичната равенка:

Ја прошируваме детерминантата со првата колона:

Ние вршиме дополнителни поедноставувања според разгледуваниот метод, избегнувајќи полином од 3 степен:

се сопствени вредности.

Ајде да ги најдеме сопствените вектори:

1) Нема потешкотии со коренот:

Немојте да се чудите, покрај комплетот, се користат и променливи - тука нема разлика.

Од 3-та равенка изразуваме - заменуваме во 1-та и 2-та равенка:

Од двете равенки следува:

Нека тогаш:

2-3) За повеќе вредности, го добиваме системот .

Дозволете ни да ја запишеме матрицата на системот и, користејќи елементарни трансформации, да ја доведеме во скалеста форма:

www.сајтви овозможува да најдете. Сајтот ја прави пресметката. За неколку секунди, серверот ќе го даде правилното решение. Карактеристичната равенка за матрицатаќе биде алгебарски израз пронајден со правилото за пресметување на детерминантата матрици матрици, додека на главната дијагонала ќе има разлики во вредностите на дијагоналните елементи и променливата. При пресметување карактеристична равенка за матрица онлајн, секој елемент матрициќе се помножи со соодветните други елементи матрици. Најдете во режим онлајнможно само за квадрат матрици. Најдете операција карактеристична равенка за матрица онлајнсе сведува на пресметување на алгебарскиот збир на производот на елементите матрицикако резултат на наоѓање на детерминантата матрици, само заради утврдување карактеристична равенка за матрица онлајн. Оваа операција зазема посебно место во теоријата матрици, ви овозможува да пронајдете сопствени вредности и вектори користејќи корени. Наоѓање задача карактеристична равенка за матрица онлајне да се множат елементи матрицисо последователно сумирање на овие производи според одредено правило. www.сајтнаоѓа карактеристична равенка за матрицададена димензија во режимот онлајн. пресметка карактеристична равенка за матрица онлајнза дадена димензија, ова е наоѓање полином со нумерички или симболички коефициенти пронајдени според правилото за пресметување на детерминантата матрици- како збир од производите на соодветните елементи матрици, само заради утврдување карактеристична равенка за матрица онлајн. Наоѓање полином во однос на променлива за квадрат матрици, како дефиниција карактеристична равенка за матрицата, вообичаено во теоријата матрици. Вредноста на корените на полиномот карактеристична равенка за матрица онлајнсе користи за дефинирање на сопствени вектори и сопствени вредности за матрици. Меѓутоа, ако детерминантата матрицитогаш ќе биде нула матрична карактеристика равенкасепак ќе постои, за разлика од обратното матрици. Со цел да се пресмета карактеристична равенка за матрицаили побарајте неколку одеднаш матрици карактеристични равенки, треба да потрошите многу време и напор, додека нашиот сервер ќе најде карактеристична равенка за онлајн матрица. Во овој случај, одговорот со наоѓање карактеристична равенка за матрица онлајнќе биде точен и со доволна точност, дури и ако бројките при наоѓање карактеристична равенка за матрица онлајнќе биде ирационален. На страницата www.сајтзаписите на знаци се дозволени во елементи матрици, тоа е карактеристична равенка за онлајн матрицаможе да се претстави во општа симболичка форма при пресметувањето матрица за карактеристични равенки онлајн. Корисно е да се провери добиениот одговор при решавање на проблемот со наоѓање карактеристична равенка за матрица онлајнкористење на страницата www.сајт. При извршување на операцијата пресметување на полином - карактеристична равенка на матрицата, потребно е да се биде внимателен и крајно концентриран во решавањето на овој проблем. За возврат, нашата страница ќе ви помогне да ја проверите вашата одлука на темата матрица за карактеристични равенки онлајн. Ако немате време за долги проверки на решените проблеми, тогаш www.сајтсигурно ќе биде погодна алатка за проверка при наоѓање и пресметување карактеристична равенка за матрица онлајн.

Својствектор на квадратна матрица е оној кој, кога се множи со дадена матрица, резултира со колинеарен вектор. Со едноставни зборови, кога матрицата се множи со сопствен вектор, вториот останува иста, но се множи со некој број.

Дефиниција

Сопствениот вектор е ненулта вектор V, кој, кога ќе се помножи со квадратна матрица M, станува сам по себе, зголемен за одреден број λ. Во алгебарска нотација, ова изгледа вака:

M × V = λ × V,

каде λ е сопствена вредност на матрицата M.

Да разгледаме нумерички пример. За погодност при пишувањето, броевите во матрицата ќе бидат одделени со точка-запирка. Да речеме дека имаме матрица:

• М = 0; четири;
• 6; 10.

Ајде да го помножиме со вектор на колона:

• V = -2;

Кога множиме матрица со вектор на колона, добиваме и вектор на колона. Во строг математички јазик, формулата за множење на матрица 2 × 2 со вектор на колона би изгледала вака:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 значи елемент од матрицата M, кој стои во првиот ред и првата колона, а M22 е елементот што се наоѓа во вториот ред и втората колона. За нашата матрица, овие елементи се M11 = 0, M12 = 4, M21 = 6, M22 10. За вектор на колона, овие вредности се V11 = –2, V21 = 1. Според оваа формула, го добиваме следново резултат на производот на квадратна матрица со вектор:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

За погодност, го запишуваме векторот на колоната во ред. Значи, ја помноживме квадратната матрица со векторот (-2; 1), што резултира со векторот (4; -2). Очигледно, ова е истиот вектор помножен со λ = -2. Ламбда во овој случај означува сопствена вредност на матрицата.

Сопствениот вектор на матрицата е колинеарен вектор, односно објект што не ја менува својата позиција во просторот кога се множи со матрица. Концептот на колинеарност во векторската алгебра е сличен на терминот паралелизам во геометријата. Во геометриската интерпретација, колинеарните вектори се паралелно насочени сегменти со различни должини. Од времето на Евклид, знаеме дека една права има бесконечен број на прави паралелни со неа, па логично е да се претпостави дека секоја матрица има бесконечен број сопствени вектори.

Од претходниот пример, може да се види дека и (-8; 4), и (16; -8), и (32, -16) можат да бидат сопствени вектори. Сите овие се колинеарни вектори што одговараат на сопствената вредност λ = -2. При множење на оригиналната матрица со овие вектори, сепак ќе добиеме вектор како резултат, кој се разликува од оригиналот за 2 пати. Затоа, при решавање на задачи за наоѓање сопствен вектор, потребно е да се најдат само линеарно независни векторски објекти. Најчесто, за n × n матрица, има n-ти број на сопствени вектори. Нашиот калкулатор е дизајниран за анализа на квадратни матрици од втор ред, така што речиси секогаш ќе се најдат два сопствени вектори како резултат, освен кога се совпаѓаат.

Во примерот погоре, однапред го знаевме сопствениот вектор на оригиналната матрица и визуелно го одредивме бројот на ламбда. Меѓутоа, во пракса, сè се случува обратно: на почетокот има сопствени вредности и дури потоа сопствени вектори.

Алгоритам за решение

Ајде повторно да ја погледнеме оригиналната матрица M и да се обидеме да ги најдеме двата нејзини сопствени вектори. Значи, матрицата изгледа вака:

• М = 0; четири;
• 6; 10.

За почеток, треба да ја одредиме сопствената вредност λ, за која треба да ја пресметаме детерминантата на следнава матрица:

• (0 − λ); четири;
• 6; (10 − λ).

Оваа матрица се добива со одземање на непознатата λ од елементите на главната дијагонала. Детерминантата се одредува со стандардната формула:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Бидејќи нашиот вектор не смее да биде нула, ја земаме добиената равенка како линеарно зависна и ја изедначуваме нашата детерминанта detA на нула.

(0 − λ) × (10 − λ) − 24 = 0

Ајде да ги отвориме заградите и да ја добиеме карактеристичната равенка на матрицата:

λ 2 − 10λ − 24 = 0

Ова е стандардна квадратна равенка која треба да се реши во однос на дискриминаторката.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Коренот на дискриминаторот е sqrt(D) = 14, значи λ1 = -2, λ2 = 12. Сега за секоја ламбда вредност, треба да најдеме сопствен вектор. Да ги изразиме коефициентите на системот за λ = -2.

• M − λ × E = 2; четири;
• 6; 12.

Во оваа формула, Е е матрицата на идентитетот. Врз основа на добиената матрица, составуваме систем од линеарни равенки:

2x + 4y = 6x + 12y

каде x и y се елементи на сопствениот вектор.

Ајде да ги собереме сите X лево и сите Y од десната страна. Очигледно - 4x = 8y. Поделете го изразот со - 4 и добијте x = -2y. Сега можеме да го одредиме првиот сопствен вектор на матрицата земајќи ги сите вредности на непознатите (запомнете за бесконечноста на линеарно зависните сопствени вектори). Да земеме y = 1, а потоа x = -2. Затоа, првиот сопствен вектор изгледа како V1 = (–2; 1). Врати се на почетокот на статијата. Токму со овој векторски објект ја помноживме матрицата за да го демонстрираме концептот на сопствен вектор.

Сега да го најдеме сопствениот вектор за λ = 12.

• M - λ × E = -12; четири
• 6; -2.

Да го составиме истиот систем на линеарни равенки;

• -12x + 4y = 6x − 2y
• -18x = -6г
• 3x=y.

Сега да земеме x = 1, па оттука y = 3. Така, вториот сопствен вектор изгледа како V2 = (1; 3). При множење на оригиналната матрица со овој вектор, резултатот секогаш ќе биде истиот вектор помножен со 12. Ова го комплетира алгоритмот за решение. Сега знаете како рачно да дефинирате сопствен вектор на матрицата.

• детерминанта;
• трага, односно збир на елементите на главната дијагонала;
• ранг, односно максимален број на линеарно независни редови/колони.

Програмата работи според горенаведениот алгоритам, минимизирајќи го процесот на решавање. Важно е да се истакне дека во програмата ламбда се означува со буквата „в“. Ајде да погледнеме нумерички пример.

Пример за програма

Ајде да се обидеме да дефинираме сопствени вектори за следната матрица:

• М=5; 13;
• 4; 14.

Ајде да ги внесеме овие вредности во ќелиите на калкулаторот и да го добиеме одговорот во следната форма:

• Ранг на матрица: 2;
• Детерминанта на матрицата: 18;
• Матрична трага: 19;
• Пресметка на сопствени вектори: c 2 − 19.00c + 18.00 (карактеристична равенка);
• Пресметка на сопствени вектори: 18 (прва ламбда вредност);
• Пресметка на сопствени вектори: 1 (втора ламбда вредност);
• Систем на равенки на векторот 1: -13x1 + 13y1 = 4x1 − 4y1;
• Систем на равенки на вектор 2: 4x1 + 13y1 = 4x1 + 13y1;
• Сопствен вектор 1: (1; 1);
• Својствектор 2: (-3,25; 1).

Така, добивме два линеарно независни сопствени вектори.

Заклучок

Линеарна алгебра и аналитичка геометрија се стандардни предмети за секој бруцош по инженерство. Голем број вектори и матрици е застрашувачки и лесно е да се направи грешка во таквите гломазни пресметки. Нашата програма ќе им овозможи на студентите да ги проверат своите пресметки или автоматски да го решат проблемот со наоѓање сопствен вектор. Во нашиот каталог има и други линеарни алгебарски калкулатори, користете ги во вашето учење или работа.

". Првиот дел ги прикажува одредбите кои се минимално неопходни за разбирање на хемометријата, а вториот дел ги содржи фактите што треба да ги знаете за подлабоко разбирање на методите на мултиваријатна анализа. Презентацијата е илустрирана со примери направени во работна книга на Excel Матрица.xlsшто го придружува овој документ.

Врските до примерите се ставаат во текстот како објекти на Excel. Овие примери се од апстрактна природа, тие во никој случај не се поврзани со проблемите на аналитичката хемија. Вистинските примери за употреба на матрична алгебра во хемометријата се дискутирани во други текстови посветени на различни хемометриски апликации.

Повеќето од мерењата извршени во аналитичката хемија не се директни, туку индиректно. Тоа значи дека во експериментот наместо вредноста на саканиот аналит C (концентрација) се добива друга вредност x(сигнал) поврзан со, но не еднаков на C, т.е. x(C) ≠ C. Како по правило, типот на зависност x(C) не е познато, но за среќа во аналитичката хемија повеќето мерења се пропорционални. Тоа значи дека како што е концентрацијата на С во апати, сигналот X ќе се зголеми за иста количина., т.е. x(аВ) = а x(В). Покрај тоа, сигналите се и адитивни, така што сигналот од примерок кој содржи две супстанции со концентрации C 1 и C 2 ќе биде еднаков на збирот на сигналите од секоја компонента, т.е. x(C1 + C2) = x(C1)+ x(C2). Пропорционалноста и адитивноста заедно даваат линеарност. Може да се дадат многу примери за да се илустрира принципот на линеарност, но доволно е да се споменат два од највпечатливите примери - хроматографија и спектроскопија. Втората карактеристика својствена за експериментот во аналитичката хемија е повеќеканален. Современата аналитичка опрема истовремено ги мери сигналите за многу канали. На пример, интензитетот на пренос на светлина се мери за неколку бранови должини одеднаш, т.е. спектар. Затоа, во експериментот имаме работа со различни сигнали x 1 , x 2 ,...., x n карактеризирање на множеството концентрации C 1 , C 2 , ..., C m на супстанции присутни во системот што се проучува.

Ориз. 1 Спектра

Значи, аналитичкиот експеримент се карактеризира со линеарност и мултидимензионалност. Затоа, погодно е експерименталните податоци да се земат предвид како вектори и матрици и да се манипулира со нив користејќи го апаратот на матрична алгебра. Плодноста на овој пристап е илустрирана со примерот прикажан во , кој покажува три спектри земени за 200 бранови должини од 4000 до 4796 cm–1. Првиот ( x 1) и второ ( x 2) спектрите се добиени за стандардни примероци во кои се познати концентрациите на две супстанции А и Б: во првиот примерок [A] = 0,5, [B] = 0,1, а во вториот примерок [A] = 0,2, [ B] = 0,6. Што може да се каже за нов, непознат примерок, чиј спектар е наведен x 3 ?

Размислете за три експериментални спектри x 1 , x 2 и x 3 како три вектори со димензија 200. Користејќи линеарна алгебра, лесно може да се покаже тоа x 3 = 0.1 x 1 +0.3 x 2 , така што третиот примерок очигледно содржи само супстанции А и Б во концентрации [A] = 0,5×0,1 + 0,2×0,3 = 0,11 и [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Основни информации

1.1 Матрици

Матрицанаречена правоаголна табела со броеви, на пример

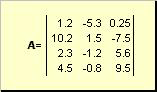
Ориз. 2 Матрица

Матриците се означуваат со големи задебелени букви ( А), а нивните елементи - со соодветните мали букви со индекси, т.е. а ij . Првиот индекс ги нумерира редовите, а вториот ги брои колоните. Во хемометријата, вообичаено е максималната вредност на индексот да се означи со истата буква како и самиот индекс, но со големи букви. Затоа, матрицата Аможе да се напише и како ( а ij , јас = 1,..., Јас; ј = 1,..., Ј). За пример матрицата Јас = 4, Ј= 3 и а 23 = −7.5.

Пар броеви Јаси Јсе нарекува димензија на матрицата и се означува како Јас× Ј. Пример за матрица во хемометријата е збир на спектри добиени за Јаспримероци на Јбранови должини.

1.2. Наједноставните операции со матрици

Матриците можат множете се со броеви. Во овој случај, секој елемент се множи со овој број. На пример -

Ориз. 3 Множење на матрица со број

Две матрици со иста димензија можат да бидат елементарно превиткувањеи одзема. На пример,

Ориз. 4 Собирање на матрица

Како резултат на множење со број и собирање, се добива матрица со иста димензија.

Нулта матрица е матрица која се состои од нули. Таа е назначена О. Очигледно е дека А+О = А, А−А = Ои 0 А = О.

Матрицата може транспонираат. За време на оваа операција, матрицата се превртува, т.е. редовите и колоните се заменуваат. Транспозицијата е означена со цртичка, А“ или индекс Ат . Така, ако А = {а ij , јас = 1,..., Јас; ј = 1,...,Ј), тогаш А t = ( а џи , ј = 1,...,Ј; јас = 1,..., Јас). На пример

Ориз. 5 Транспозиција на матрица

Очигледно е дека ( Ат) т = А, (А+Б) т = А t+ Бт .

1.3. Множење на матрицата

Матриците можат размножуваат, но само доколку имаат соодветни димензии. Зошто е тоа така ќе биде јасно од дефиницијата. Матричен производ А, димензија Јас× Ки матрици Б, димензија К× Ј, се нарекува матрица В, димензија Јас× Ј, чии елементи се броеви

Така за производот АБпотребно е бројот на колони во левата матрица Абеше еднаков на бројот на редови во десната матрица Б. Пример за матричен производ -

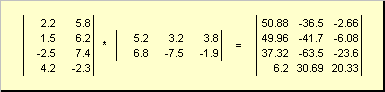
Сл.6 Производ на матрици

Правилото за множење на матрицата може да се формулира на следниов начин. Да се ​​најде елемент од матрицата Встоејќи на раскрсницата јас-та линија и ј-та колона ( в ij) мора да се множи елемент по елемент јас-ти ред од првата матрица Ана ј-та колона од втората матрица Би соберете ги сите резултати. Така, во прикажаниот пример, елементот од третиот ред и втората колона се добиваат како збир од производите според елементот од третиот ред Аи втора колона Б

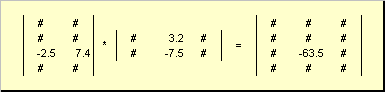
Сл.7 Елемент на производот на матрици

Производот на матриците зависи од редоследот, т.е. АБ ≠ БА, барем од димензионални причини. Се вели дека е некомутативен. Меѓутоа, производот на матриците е асоцијативен. Тоа значи дека ABC = (АБ)В = А(п.н.е). Згора на тоа, тој е и дистрибутивен, т.е. А(Б+В) = АБ+AC. Очигледно е дека АО = О.

1.4. Квадратни матрици

Ако бројот на колони на матрицата е еднаков на бројот на нејзините редови ( Јас = J=N), тогаш таквата матрица се нарекува квадрат. Во овој дел, ќе разгледаме само такви матрици. Меѓу овие матрици, може да се издвојат матрици со посебни својства.

Осаменматрица (означено Јаса понекогаш Е) е матрица во која сите елементи се еднакви на нула, освен дијагоналните, кои се еднакви на 1, т.е.

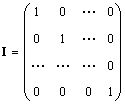
Очигледно ВИ = IA = А.

Матрицата се нарекува дијагонала, ако сите негови елементи, освен дијагоналните ( а ii) се еднакви на нула. На пример

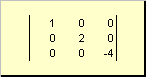
Ориз. 8 Дијагонална матрица

Матрица Анаречен врв триаголен, ако сите негови елементи што лежат под дијагоналата се еднакви на нула, т.е. а ij= 0, во јас>ј. На пример

Ориз. 9 Горна триаголна матрица

Долната триаголна матрица е дефинирана слично.

Матрица Аповикани симетрични, ако А t = А. Со други зборови а ij = а џи. На пример

Ориз. 10 Симетрична матрица

Матрица Аповикани ортогонални, ако

Ат А = АА t = Јас.

Матрицата се нарекува нормалноако

1.5. Трага и одредница

Следиквадратна матрица А(означува Тр( А) или Sp( А)) е збирот на неговите дијагонални елементи,

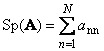
На пример,

Ориз. 11 Матрична трага

Очигледно е дека

Sp(α А) = α Sp( А) и

Sp( А+Б) = Sp( А)+ Sp( Б).

Може да се покаже дека

Sp( А) = Sp( А t), Sp ( Јас) = Н,

а исто така и тоа

Sp( АБ) = Sp( БА).

Друга важна карактеристика на квадратната матрица е нејзината детерминанта(означено со det( А)). Дефиницијата на детерминантата во општиот случај е прилично комплицирана, затоа ќе започнеме со наједноставната опција - матрицата Адимензија (2×2). Потоа

За матрица (3×3), детерминантата ќе биде еднаква на

Во случај на матрица ( Н× Н) детерминантата се пресметува како збир 1 2 3 ... Н= Н! термини, од кои секоја е еднаква на

Индекси к 1 , к 2 ,..., к Нсе дефинираат како сите можни подредени пермутации рброеви во множеството (1, 2, ... , Н). Пресметката на детерминантата на матрицата е сложена процедура, која во пракса се спроведува со помош на специјални програми. На пример,

Ориз. 12 Матрична детерминанта

Ги забележуваме само очигледните својства:

Дет( Јас) = 1, дет( А) = Дет( Ат),

Дет( АБ) = Дет( А)дет( Б).

1.6. Вектори

Ако матрицата има само една колона ( Ј= 1), тогаш се нарекува таков објект вектор. Поточно, вектор на колона. На пример

Може да се разгледаат и матрици кои се состојат од еден ред, на пример

Овој објект е исто така вектор, но вектор на ред. Кога се анализираат податоците, важно е да се разбере со кои вектори имаме работа - колони или редови. Значи, спектарот земен за еден примерок може да се смета како вектор на ред. Тогаш множеството на спектрални интензитети на одредена бранова должина за сите примероци треба да се третира како вектор на колона.

Димензијата на векторот е бројот на неговите елементи.

Јасно е дека секој вектор на колона може да се трансформира во вектор на ред со транспозиција, т.е.

Во оние случаи кога формата на вектор не е конкретно специфицирана, туку едноставно се кажува вектор, тогаш тие значат вектор на колона. Ние исто така ќе се придржуваме до ова правило. Векторот се означува со мала директна задебелена буква. Нулта вектор е вектор чии сите елементи се еднакви на нула. Се означува 0 .

1.7. Наједноставните операции со вектори

Векторите може да се додаваат и множат со броеви на ист начин како и матриците. На пример,

Ориз. 13 Операции со вектори

Два вектори xи yповикани колинеарна, ако има број α таков што

1.8. Производи на вектори

Два вектори со иста димензија Нможе да се множи. Нека има два вектори x = (x 1 , x 2 ,...,x N) т и y = (y 1 , y 2 ,...,y N) т. Водени од правилото за множење „ред по колона“, можеме да направиме два производа од нив: xт yи xyт . Првата работа

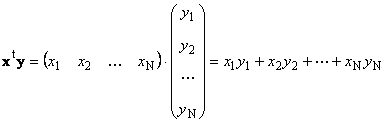
повикани скаларенили внатрешен. Нејзиниот резултат е бројка. Ја користи и ознаката ( x,y)= xт y. На пример,

Ориз. 14 Внатрешен (скаларен) производ

Втора работа

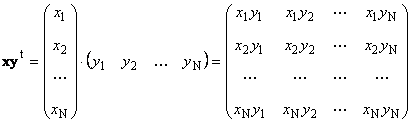
повикани надворешен. Неговиот резултат е матрица на димензии ( Н× Н). На пример,

Ориз. 15 Надворешен производ

Се нарекуваат вектори чиј скаларен производ е еднаков на нула ортогонални.

1.9. Векторска норма

Скаларниот производ на векторот со себе се нарекува скаларен квадрат. Оваа вредност

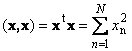
дефинира квадрат должинавектор x. За да се означи должината (исто така наречена норматавектор) се користи ознаката

На пример,

Ориз. 16 Векторска норма

Единица должина вектор (|| x|| = 1) се нарекува нормализиран. Вектор без нула ( x ≠ 0 ) може да се нормализира со делење со должината, т.е. x = ||x|| (x/||x||) = ||x|| д. Еве д = x/||x|| е нормализиран вектор.

Векторите се нарекуваат ортонормални ако сите се нормализирани и во пар ортогонални.

1.10. Агол помеѓу вектори

Скаларниот производ дефинира и аголφ помеѓу два вектори xи y

Ако векторите се ортогонални, тогаш cosφ = 0 и φ = π/2, а ако се колинеарни, тогаш cosφ = 1 и φ = 0.

1.11. Векторско претставување на матрица

Секоја матрица Аголемина Јас× Јможе да се претстави како множество вектори

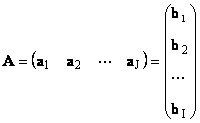
Тука секој вектор а је ј-вектор на колона и ред б јасе јас-ти ред од матрицата А

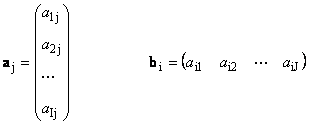
1.12. Линеарно зависни вектори

Вектори со иста димензија ( Н) може да се додаде и множи со број, исто како и матриците. Резултатот е вектор со иста димензија. Нека има неколку вектори со иста димензија x 1 , x 2 ,...,x K и ист број на броеви α α 1 , α 2 ,...,α К. Вектор

y= α 1 x 1 + α 2 x 2 +...+α К x К

повикани линеарна комбинацијавектори x к .

Ако има такви ненула броеви α к ≠ 0, к = 1,..., К, што y = 0 , тогаш такво множество вектори x кповикани линеарно зависни. Во спротивно, векторите се нарекуваат линеарно независни. На пример, вектори x 1 = (2, 2) t и x 2 = (−1, −1) t се линеарно зависни, бидејќи x 1 +2x 2 = 0

1.13. Ранг на матрица

Размислете за збир на Квектори x 1 , x 2 ,...,x Кдимензии Н. Рангот на овој систем на вектори е максималниот број на линеарно независни вектори. На пример во сетот

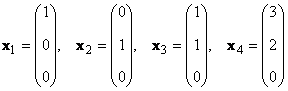
има само два линеарно независни вектори, на пример x 1 и x 2, така што неговиот ранг е 2.

Очигледно, ако има повеќе вектори во множеството од нивната димензија ( К>Н), тогаш тие се нужно линеарно зависни.

Ранг на матрица(означено со ранг) А)) е ранг на системот на вектори од кој се состои. Иако секоја матрица може да се претстави на два начина (вектори на колони или вектори на ред), тоа не влијае на вредноста на рангирањето, бидејќи

1.14. инверзна матрица

квадратна матрица Асе нарекува недегенериран ако има единствен обратноматрица А-1 , утврдени со условите

АА −1 = А −1 А = Јас.

Инверзната матрица не постои за сите матрици. Неопходен и доволен услов за недегенерација е

Дет( А) ≠ 0 или ранг ( А) = Н.

Инверзијата на матрицата е сложена процедура за која постојат посебни програми. На пример,

Ориз. 17 Инверзија на матрица

Даваме формули за наједноставниот случај - матрици 2 × 2

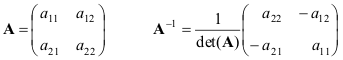
Доколку матриците Аи Бтогаш се недегенерирани

(АБ) −1 = Б −1 А −1 .

1.15. Псевдо-инверзна матрица

Доколку матрицата Ае дегенериран и инверзната матрица не постои, тогаш во некои случаи може да се користи псевдоинверзнаматрица, која е дефинирана како таква матрица А+ тоа

АА + А = А.

Псевдо-инверзната матрица не е единствената и нејзината форма зависи од методот на изградба. На пример, за правоаголна матрица, можете да го користите методот Мур-Пенроуз.

Ако бројот на колони е помал од бројот на редови, тогаш

А + =(Ат А) −1 Ат

На пример,

Ориз. 17а Инверзија на псевдо матрица

Ако бројот на колони е поголем од бројот на редови, тогаш

А + =Ат ( ААт) −1

1.16. Множење на вектор со матрица

Вектор xможе да се помножи со матрица Асоодветна димензија. Во овој случај, векторот на колоната се множи десно Секира, а векторската низа е лево xт А. Ако димензијата на векторот Ј, и димензијата на матрицата Јас× Јтогаш резултатот е вектор на димензија Јас. На пример,

Ориз. 18 Множење на векторско-матрица

Доколку матрицата А- квадрат ( Јас× Јас), потоа векторот y = Секираги има истите димензии како x. Очигледно е дека

А(α 1 x 1 + α 2 x 2) = α 1 Секира 1 + α 2 Секира 2 .

Затоа матриците може да се сметаат како линеарни трансформации на вектори. Особено x = x, Вол = 0 .

2. Дополнителни информации

2.1. Системи на линеарни равенки

Нека А- големина на матрицата Јас× Ј, А б- димензионален вектор Ј. Размислете за равенката

Секира = б

во однос на векторот x, димензии Јас. Во суштина, ова е систем на Јаслинеарни равенки со Јнепознат x 1 ,...,x Ј. Решението постои ако и само ако

ранг ( А) = ранг ( Б) = Р,

каде Бе матрицата со зголемени димензии Јас×( J+1) кој се состои од матрицата А, поместена со колона б, Б = (А б). Во спротивно, равенките се неконзистентни.

Ако Р = Јас = Ј, тогаш решението е единствено

x = А −1 б.

Ако Р < Јас, тогаш има многу различни решенија кои можат да се изразат во смисла на линеарна комбинација Ј−Рвектори. Систем на хомогени равенки Секира = 0 со квадратна матрица А (Н× Н) има нетривијално решение ( x ≠ 0 ) ако и само ако det( А) = 0. Ако Р= ранг ( А)<Н, потоа има Н−Рлинеарно независни решенија.

2.2. Билинеарни и квадратни форми

Ако Ае квадратна матрица и xи y- вектори од соодветната димензија, потоа скаларниот производ на формата xт Ајповикани биланеарнаобликот дефиниран со матрицата А. На x = yизразување xт Секираповикани квадратниформа.

2.3. Позитивни дефинитивни матрици

квадратна матрица Аповикани позитивно дефинитивно, ако за кој било ненулти вектор x ≠ 0 ,

xт Секира > 0.

На негативен (xт Секира < 0), не-негативни (xт Секира≥ 0) и непозитивни (xт Секира≤ 0) одредени матрици.

2.4. Холески распаѓање

Ако симетричната матрица Ае позитивно определена, тогаш постои единствена триаголна матрица Усо позитивни елементи, за кои

А = Ут У.

На пример,

Ориз. 19 Холески распаѓање

2.5. поларно распаѓање

Нека Ае недегенерирана квадратна матрица на димензија Н× Н. Потоа, постои единствена поларнаперформанси

А = СР,

каде Се ненегативна симетрична матрица и Ре ортогонална матрица. матрици Си Рможе да се дефинира експлицитно:

С 2 = ААт или С = (ААт) ½ и Р = С −1 А = (ААт) −½ А.

На пример,

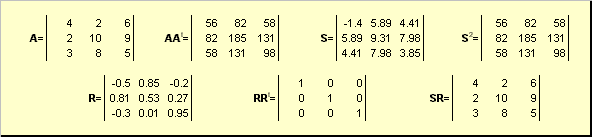
Ориз. 20 Поларно распаѓање

Доколку матрицата Ае дегенерирано, тогаш распаѓањето не е единствено - имено: Суште сама, но Рможе да ги има многу. Поларното распаѓање претставува матрица Акако комбинација на компресија/истегнување Си вртење Р.

2.6. Сопствени вектори и сопствени вредности

Нека Ае квадратна матрица. Вектор vповикани сопствен векторматрици А, ако

Ав = λ v,

каде што се нарекува бројот λ сопствена вредностматрици А. Така, трансформацијата што ја врши матрицата Анад вектор v, се сведува на едноставно истегнување или компресија со фактор λ. Сопствениот вектор се одредува до множење со константата α ≠ 0, т.е. ако vе сопствен вектор, а потоа α vе исто така сопствен вектор.

2.7. Сопствени вредности

На матрицата А, димензија ( Н× Н) не може да биде поголема од Нсопствени вредности. Задоволуваат карактеристична равенка

Дет( А − λ Јас) = 0,

што е алгебарска равенка Н-ти ред. Особено, за матрица 2×2, карактеристичната равенка ја има формата

На пример,

Ориз. 21 Сопствени вредности

Збир на сопствени вредности λ 1 ,..., λ Нматрици Аповикани спектар А.

Спектарот има различни својства. Особено

Дет( А) = λ 1×...×λ Н, Sp ( А) = λ 1 +...+λ Н.

Сопствените вредности на произволна матрица можат да бидат сложени броеви, но ако матрицата е симетрична ( А t = А), тогаш неговите сопствени вредности се реални.

2.8. Сопствени вектори

На матрицата А, димензија ( Н× Н) не може да биде поголема од Нсопствени вектори, од кои секоја одговара на сопствената вредност. Да се ​​определи сопствениот вектор v nтреба да решите систем на хомогени равенки

(А − λ n Јас)v n = 0 .

Има нетривијално решение бидејќи дет( А-λ n Јас) = 0.

На пример,

Ориз. 22 Сопствени вектори

Сопствените вектори на симетричната матрица се ортогонални.