Lag alle mulige kombinasjoner av tall online. Kombinatorikk: grunnleggende regler og formler

La oss vurdere problemet med å telle antall prøver fra et gitt sett i generell form. La det være et sett N, bestående av n elementer. Enhver undergruppe som består av m elementer kan vurderes uten å ta hensyn til rekkefølgen deres, eller ta hensyn til den, dvs. når du endrer rekkefølgen, flytt til en annen m– prøvetaking.

La oss formulere følgende definisjoner:

Plasseringer uten repetisjon

Plassering uten repetisjon avn elementer avm Ninneholdermulike elementer.

Av definisjonen følger det at de to arrangementene skiller seg fra hverandre, både i sine elementer og i sin rekkefølge, selv om elementene er like.

Teorem 3. Antall plasseringer uten repetisjon er lik produktet m faktorer, hvorav den største er antallet n . Skrive ned:

Permutasjoner uten repetisjon

Permutasjoner fran elementer kalles forskjellige rekkefølger av et settN.

Av denne definisjonen følger det at de to permutasjonene bare er forskjellige i rekkefølgen av elementene, og de kan betraktes som et spesielt tilfelle av plasseringer.

Teorem 4. Antall forskjellige permutasjoner uten repetisjon beregnes av formelen

Kombinasjoner uten repetisjoner

En kombinasjon uten repetisjon avn elementer avm enhver uordnet delmengde av et sett kallesNinneholderm ulike elementer.

Av definisjonen følger det at de to kombinasjonene bare er forskjellige i elementer; rekkefølgen er ikke viktig.

Teorem 5. Antall kombinasjoner uten repetisjoner beregnes ved å bruke en av følgende formler:

Eksempel 1. Det er 5 stoler i rommet. På hvor mange måter kan du plassere dem på dem?

a) 7 personer; b) 5 personer; c) 3 personer?

Løsning: a) Først av alt må du velge 5 personer av 7 for å sitte på stoler. Det kan gjøres
vei. Med hvert valg av en spesifikk fem, kan du produsere
omorganiseringer. I følge multiplikasjonsteoremet er det nødvendige antallet landingsmetoder likt.

Kommentar: Problemet kan løses ved å bruke bare produktteoremet, resonnement som følger: for sitteplasser på den første stolen er det 7 alternativer, på den andre stolen er det 6 alternativer, på den tredje -5, på den 4. -4 og på 5- th -3. Da er antall måter å sette 7 personer på 5 stoler på . Løsningene ved begge metodene er konsistente, siden

b) Løsningen er åpenbar -

V) - antall valg av okkuperte stoler.

- antall seter for tre personer på tre utvalgte stoler.

Det totale antallet valg er .

Det er ikke vanskelig å sjekke formlene
;

;

Antallet av alle delmengder av et sett som består av n elementer.

Gjenta plasseringer

Ved å plassere med repetisjon fran elementer avm hvert bestilte delsett av et sett kallesN, bestående avm elementer slik at et hvilket som helst element kan inkluderes i denne delmengden fra 1 tilmganger, eller være helt fraværende.

Antall plasseringer med repetisjon er angitt med og beregnes ved hjelp av formelen, som er en konsekvens av multiplikasjonssetningen:

Eksempel 2. La N = (a, b, c) være et sett med tre bokstaver. La oss kalle ethvert sett med bokstaver som er inkludert i dette settet for et ord. La oss finne antall ord med lengde 2 som kan lages fra disse bokstavene:
.

Kommentar: Selvsagt kan også plasseringer med repetisjon vurderes når
.

Eksempel 3. Du må bruke bokstavene (a, b) for å lage alle mulige ord med lengde 3. På hvor mange måter kan dette gjøres?

Svar:

I denne artikkelen vil vi snakke om en spesiell gren av matematikk kalt kombinatorikk. Formler, regler, eksempler på problemløsning – alt dette finner du her ved å lese artikkelen helt til slutt.

Så hva er denne delen? Kombinatorikk tar for seg spørsmålet om å telle objekter. Men i dette tilfellet er ikke gjenstandene plommer, pærer eller epler, men noe annet. Kombinatorikk hjelper oss å finne sannsynligheten for en hendelse. For eksempel når man spiller kort – hva er sannsynligheten for at motstanderen har et trumfkort? Eller dette eksemplet: hva er sannsynligheten for at du får en hvit fra en pose med tjue klinkekuler? Det er for denne typen problemer vi trenger å vite i det minste det grunnleggende om denne grenen av matematikk.

Kombinatoriske konfigurasjoner

Med tanke på spørsmålet om grunnleggende konsepter og formler for kombinatorikk, kan vi ikke unngå å ta hensyn til kombinatoriske konfigurasjoner. De brukes ikke bare til å formulere, men også til å løse ulike eksempler.Eksempler på slike modeller er:

• overnatting;
• omorganisering;
• kombinasjon;
• tallsammensetning;
• dele et tall.

Vi vil snakke om de tre første mer detaljert senere, men vi vil ta hensyn til komposisjon og partisjonering i denne delen. Når de snakker om sammensetningen av et bestemt tall (for eksempel a), mener de å representere tallet a som en ordnet sum av visse positive tall. Og en skillevegg er en uordnet sum.

Seksjoner

Før vi går direkte til formlene for kombinatorikk og vurdering av problemer, er det verdt å ta hensyn til det faktum at kombinatorikk, som andre grener av matematikken, har sine egne underseksjoner. Disse inkluderer:

• enumerativ;
• strukturell;
• ekstrem;
• Ramsey teori;
• sannsynlighet;
• topologisk;
• uendelig.

I det første tilfellet snakker vi om kalkulativ kombinatorikk; problemene vurderer opptelling eller telling av forskjellige konfigurasjoner som er dannet av elementer av sett. Som regel er det pålagt noen begrensninger for disse settene (særpreg, umulig å skille, mulighet for repetisjon og så videre). Og antallet av disse konfigurasjonene beregnes ved å bruke reglene for addisjon eller multiplikasjon, som vi vil snakke om litt senere. Strukturell kombinatorikk inkluderer teoriene om grafer og matroider. Et eksempel på et ekstremal kombinatorisk problem er hva som er den største dimensjonen til en graf som tilfredsstiller følgende egenskaper... I fjerde avsnitt nevnte vi Ramsey-teorien, som studerer tilstedeværelsen av regulære strukturer i tilfeldige konfigurasjoner. Probabilistisk kombinatorikk er i stand til å svare på spørsmålet - hva er sannsynligheten for at et gitt sett har en viss egenskap. Som du kanskje gjetter, bruker topologisk kombinatorikk metoder i topologi. Og til slutt, det syvende punktet - infinitær kombinatorikk studerer anvendelsen av kombinatoriske metoder på uendelige sett.

Tilleggsregel

Blant kombinatoriske formler kan du finne ganske enkle, som vi har vært kjent med ganske lenge. Et eksempel er sumregelen. Anta at vi får to handlinger (C og E), hvis de er gjensidig utelukkende, kan handling C utføres på flere måter (for eksempel a), og handling E kan utføres på b-veier, så kan hvilken som helst av dem ( C eller E) kan utføres på a + b måter.

I teorien er dette ganske vanskelig å forstå; vi vil prøve å formidle hele poenget ved å bruke et enkelt eksempel. La oss ta gjennomsnittlig antall elever i en klasse – la oss si at det er tjuefem. Blant dem er femten jenter og ti gutter. En person på vakt er tildelt hver klasse hver dag. Hvor mange måter er det å utnevne en klassemonitor i dag? Løsningen på problemet er ganske enkel; vi vil ty til tilleggsregelen. Oppgaveteksten sier ikke at bare gutter eller bare jenter kan være på vakt. Derfor kan det være hvilken som helst av de femten jentene eller hvilken som helst av de ti guttene. Ved å bruke sumregelen får vi et ganske enkelt eksempel som en barneskoleelev enkelt kan håndtere: 15 + 10. Etter telling får vi svaret: tjuefem. Det vil si at det bare er tjuefem måter å tildele en klasse på vakt for i dag.

Multiplikasjonsregel

De grunnleggende formlene for kombinatorikk inkluderer også multiplikasjonsregelen. La oss starte med teorien. La oss si at vi må utføre flere handlinger (a): den første handlingen utføres på 1 måter, den andre - på 2 måter, den tredje - på 3 måter, og så videre til den siste a-handlingen, utført på 3 måter. Da kan alle disse handlingene (som vi har totalt) utføres på N måter. Hvordan beregne ukjent N? Formelen vil hjelpe oss med dette: N = c1 * c2 * c3 *...* ca.

Igjen, ingenting er klart i teorien, så la oss gå videre til å vurdere et enkelt eksempel på bruk av multiplikasjonsregelen. La oss ta den samme klassen på tjuefem personer, der det er femten jenter og ti gutter. Bare denne gangen må vi velge to personer på vakt. De kan bare være gutter eller jenter, eller en gutt og en jente. La oss gå videre til den elementære løsningen av problemet. Vi velger den første personen på vakt, som vi bestemte i siste avsnitt, får vi tjuefem mulige alternativer. Den andre personen på vakt kan være hvilken som helst av de gjenværende personene. Vi hadde tjuefem studenter, vi valgte én, noe som betyr at den andre på vakt kan være hvilken som helst av de resterende tjuefire personene. Til slutt bruker vi multiplikasjonsregelen og finner at to tjenestemenn på vakt kan velges på seks hundre måter. Vi fikk dette tallet ved å multiplisere tjuefem og tjuefire.

Omorganisering

Nå skal vi se på en annen kombinatorisk formel. I denne delen av artikkelen vil vi snakke om permutasjoner. Vi foreslår å umiddelbart vurdere problemet ved å bruke et eksempel. La oss ta biljardballer, vi har n-te antall av dem. Vi må telle hvor mange alternativer det er for å ordne dem på rad, det vil si å lage et bestilt sett.

La oss begynne, hvis vi ikke har baller, så har vi også null alternativer for plassering. Og hvis vi har én kule, så er også arrangementet det samme (matematisk kan dette skrives slik: P1 = 1). De to ballene kan plasseres på to forskjellige måter: 1,2 og 2,1. Derfor er P2 = 2. Tre kuler kan ordnes på seks måter (P3 = 6): 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,2,1; 3,1,2. Hva om det ikke er tre slike baller, men ti eller femten? Det vil ta veldig lang tid å liste opp alle mulige alternativer, så kommer kombinatorikk til hjelp. Permutasjonsformelen vil hjelpe oss å finne svaret på spørsmålet som interesserer oss. Pn = n *P (n-1). Hvis vi prøver å forenkle formelen, får vi: Pn = n* (n - 1) *...* 2 * 1. Og dette er produktet av de første naturlige tallene. Dette tallet kalles faktorielt, og er betegnet som n!

La oss vurdere problemet. Hver morgen stiller rådgiveren opp i troppen sin (tjue personer). Det er tre bestevenner i troppen - Kostya, Sasha og Lesha. Hva er sannsynligheten for at de står ved siden av hverandre? For å finne svaret på spørsmålet må du dele sannsynligheten for et "godt" utfall på det totale antallet utfall. Totalt antall permutasjoner er 20! = 2,5 kvintillioner. Hvordan telle antall "gode" utfall? La oss anta at Kostya, Sasha og Lesha er en supermann. Da har vi bare atten fag. Antall permutasjoner i dette tilfellet er 18 = 6,5 kvadrillioner. Med alt dette kan Kostya, Sasha og Lesha vilkårlig bevege seg mellom seg i sine udelelige tre, og det er 3 til! = 6 alternativer. Det betyr at vi har 18 «gode» arrangementer totalt! *3! Alt vi trenger å gjøre er å finne ønsket sannsynlighet: (18! * 3!) / 20! Som tilsvarer omtrent 0,016. Omregnet til prosenter viser det seg å være bare 1,6 %.

Overnatting

Nå skal vi se på en annen veldig viktig og nødvendig kombinatorisk formel. Plassering er vår neste utgave, som vi inviterer deg til å vurdere i denne delen av artikkelen. Vi går for komplikasjoner. Anta at vi ønsker å vurdere mulige permutasjoner, ikke fra hele settet (n), men fra en mindre (m). Det vil si at vi vurderer permutasjoner av n elementer med m.

De grunnleggende formlene for kombinatorikk bør ikke bare huskes, men forstås. Selv om de blir mer kompliserte, siden vi ikke har én parameter, men to. Anta at m = 1, så A = 1, m = 2, så A = n * (n - 1). Hvis vi forenkler formelen ytterligere og går over til notasjon ved hjelp av faktorialer, får vi en helt lakonisk formel: A = n! / (n - m)!

Kombinasjon

Vi gjennomgikk nesten alle de grunnleggende kombinatoriske formlene med eksempler. La oss nå gå videre til sluttfasen av å vurdere det grunnleggende kombinatorikkkurset - bli kjent med kombinasjoner. Nå skal vi velge m varer fra den n vi har, og vi skal velge alt på alle mulige måter. Hvordan er da dette forskjellig fra plassering? Vi vil ikke ta hensyn til bestillingen. Dette uordnede settet vil være kombinasjonen.

La oss umiddelbart introdusere notasjonen: C. Vi tar plasseringen av m kuler ut av n. Vi slutter å ta hensyn til orden og ender opp med gjentatte kombinasjoner. For å få antall kombinasjoner må vi dele antall plasseringer på m! (m faktoriell). Det vil si C = A/m! Dermed er det bare noen få måter å velge mellom n baller på, som er omtrent lik antall måter å velge nesten alle på. Det er et logisk uttrykk for dette: å velge litt er det samme som å kaste ut nesten alt. Det er også viktig å nevne på dette tidspunktet at det maksimale antallet kombinasjoner kan oppnås når du prøver å velge halvparten av elementene.

Hvordan velge en formel for å løse et problem?

Vi undersøkte i detalj de grunnleggende formlene for kombinatorikk: plassering, permutasjon og kombinasjon. Nå er vår oppgave å lette valget av den nødvendige formelen for å løse et kombinatorisk problem. Du kan bruke følgende ganske enkle skjema:

1. Spør deg selv: er det tatt hensyn til rekkefølgen elementene er plassert i i oppgaveteksten?
2. Hvis svaret er nei, bruk kombinasjonsformelen (C = n! / (m! * (n - m)!)).
3. Hvis svaret er nei, må et annet spørsmål besvares: er alle elementene inkludert i kombinasjonen?
4. Hvis svaret er ja, bruk permutasjonsformelen (P = n!).
5. Hvis svaret er nei, bruk plasseringsformelen (A = n! / (n - m)!).

Eksempel

Vi så på elementer av kombinatorikk, formler og noen andre problemstillinger. La oss nå gå videre til å vurdere det virkelige problemet. Tenk deg at du har en kiwi, en appelsin og en banan foran deg.

Spørsmål én: på hvor mange måter kan de omorganiseres? For å gjøre dette bruker vi permutasjonsformelen: P = 3! = 6 måter.

Spørsmål to: på hvor mange måter kan du velge én frukt? Dette er åpenbart, vi har bare tre alternativer - velg kiwi, appelsin eller banan, men la oss bruke kombinasjonsformelen: C = 3! / (2! * 1!) = 3.

Spørsmål tre: på hvor mange måter kan du velge to frukter? Hvilke alternativer har vi til og med? Kiwi og appelsin; kiwi og banan; appelsin og banan. Det vil si at det er tre alternativer, men dette er enkelt å sjekke ved hjelp av kombinasjonsformelen: C = 3! / (1! * 2!) = 3

Spørsmål fire: På hvor mange måter kan du velge tre frukter? Som du kan se, er det bare én måte å velge tre frukter på: ta kiwi, appelsin og banan. C = 3! / (0! * 3!) = 1.

Spørsmål fem: på hvor mange måter kan du velge minst én frukt? Denne tilstanden betyr at vi kan ta en, to eller alle tre fruktene. Derfor legger vi til C1 + C2 + C3 = 3 + 3 + 1 = 7. Det vil si at vi har syv måter å ta minst én frukt fra bordet på.

Det skal bemerkes at kombinatorikk er en uavhengig gren av høyere matematikk (og ikke en del av terver), og det er skrevet tunge lærebøker om denne disiplinen, hvis innhold til tider ikke er enklere enn abstrakt algebra. En liten del av teoretisk kunnskap vil imidlertid være nok for oss, og i denne artikkelen vil jeg prøve å analysere i en tilgjengelig form det grunnleggende om emnet med typiske kombinatoriske problemer. Og mange av dere vil hjelpe meg ;-)

Hva skal vi gjøre? I en snever forstand er kombinatorikk beregningen av forskjellige kombinasjoner som kan lages fra et bestemt sett diskret gjenstander. Objekter forstås som alle isolerte gjenstander eller levende vesener - mennesker, dyr, sopp, planter, insekter, etc. Samtidig bryr kombinatorikk seg ikke i det hele tatt om at settet består av en tallerken grøtgryn, et loddejern og en sumpfrosk. Det er grunnleggende viktig at disse objektene kan telles opp - det er tre av dem (diskrethet) og det viktigste er at ingen av dem er identiske.

Vi har behandlet mye, nå om kombinasjoner. De vanligste typene kombinasjoner er permutasjoner av objekter, deres valg fra et sett (kombinasjon) og distribusjon (plassering). La oss se hvordan dette skjer akkurat nå:

Permutasjoner, kombinasjoner og plasseringer uten repetisjon

Ikke vær redd for obskure termer, spesielt siden noen av dem egentlig ikke er veldig gode. La oss starte med halen av tittelen - hva betyr " ingen repetisjoner"? Dette betyr at vi i denne delen vil vurdere sett som består av diverse gjenstander. For eksempel ... nei, jeg byr ikke på grøt med loddebolt og frosk, det er bedre å ha noe smakligere =) Tenk at et eple, en pære og en banan har materialisert seg på bordet foran deg ( hvis du har dem, kan situasjonen simuleres i virkeligheten). Vi legger ut fruktene fra venstre til høyre i følgende rekkefølge:

eple / pære / banan

Spørsmål en: På hvor mange måter kan de omorganiseres?

En kombinasjon er allerede skrevet ovenfor, og det er ingen problemer med resten:

eple / banan / pære
pære / eple / banan
pære / banan / eple
banan / eple / pære
banan / pære / eple

Total: 6 kombinasjoner eller 6 kombinasjonsmuligheter.

Ok, det var ikke vanskelig å liste opp alle mulige tilfeller, men hva om det er flere objekter? Med bare fire forskjellige frukter vil antallet kombinasjoner øke betraktelig!

Vennligst åpne referansematerialet (det er praktisk å skrive ut manualen) og i punkt nr. 2 finner du formelen for antall permutasjoner.

Ingen problemer - 3 objekter kan omorganiseres på forskjellige måter.

Spørsmål to: På hvor mange måter kan du velge a) én frukt, b) to frukter, c) tre frukter, d) minst én frukt?

Hvorfor velge? Så vi fikk opp appetitten i forrige punkt - for å spise! =)

a) Én frukt kan selvsagt velges på tre måter - ta enten et eple, en pære eller en banan. Den formelle beregningen gjennomføres iht formel for antall kombinasjoner:

Oppføringen i dette tilfellet skal forstås som følger: "på hvor mange måter kan du velge 1 frukt av tre?"

b) La oss liste opp alle mulige kombinasjoner av to frukter:

eple og pære;
eple og banan;
pære og banan.

Antall kombinasjoner kan enkelt kontrolleres med samme formel:

Oppføringen forstås på en lignende måte: "på hvor mange måter kan du velge 2 frukter av tre?"

c) Og til slutt, det er bare én måte å velge tre frukter på:

Forresten, formelen for antall kombinasjoner forblir meningsfull for en tom prøve:
På denne måten kan du ikke velge en eneste frukt - faktisk ta ingenting, og det er det.

d) På hvor mange måter kan du ta minst en frukt? Betingelsen "minst én" innebærer at vi er fornøyd med 1 frukt (hvilken som helst) eller 2 frukter eller alle 3 fruktene:
ved å bruke disse metodene kan du velge minst én frukt.

Lesere som nøye har studert den innledende leksjonen på sannsynlighetsteori, vi har allerede gjettet noe. Men mer om betydningen av plusstegnet senere.

For å svare på det neste spørsmålet trenger jeg to frivillige... ...Vel, siden ingen vil, så ringer jeg deg til styret =)

Spørsmål tre: På hvor mange måter kan du distribuere én frukt hver til Dasha og Natasha?

For å distribuere to frukter, må du først velge dem. I henhold til avsnittet "be" i det forrige spørsmålet, kan dette gjøres på måter, jeg vil skrive dem om:

eple og pære;
eple og banan;
pære og banan.

Men nå blir det dobbelt så mange kombinasjoner. Tenk for eksempel på det første paret frukt:
Du kan behandle Dasha med et eple, og Natasha med en pære;
eller omvendt - Dasha vil få pæren, og Natasha vil få eplet.

Og en slik permutasjon er mulig for hvert par frukt.

Tenk på den samme studentgruppen som gikk på dansen. På hvor mange måter kan en gutt og en jente kobles sammen?

På måter kan du velge 1 ung mann;
måter du kan velge 1 jente på.

Altså en ung mann Og Du kan velge én jente: måter.

Når 1 objekt er valgt fra hvert sett, er følgende prinsipp for å telle kombinasjoner gyldig: " hver et objekt fra ett sett kan danne et par med hver gjenstand for et annet sett."

Det vil si at Oleg kan invitere hvilken som helst av de 13 jentene til dans, Evgeny kan også invitere hvilken som helst av de tretten, og resten av ungdommene har et lignende valg. Totalt: mulige par.

Det skal bemerkes at i dette eksemplet spiller "historien" om dannelsen av paret ingen rolle; Men hvis vi tar initiativet i betraktning, må antall kombinasjoner dobles, siden hver av de 13 jentene også kan invitere hvilken som helst gutt til dans. Alt avhenger av betingelsene for en bestemt oppgave!

Et lignende prinsipp er gyldig for mer komplekse kombinasjoner, for eksempel: på hvor mange måter kan du velge to unge menn? Og to jenter til å delta i et KVN-spill?

Union OG antyder tydelig at kombinasjonene må multipliseres:

Mulige kunstnergrupper.

Med andre ord, Hver et guttepar (45 unike par) kan opptre med noen et par jenter (78 unike par). Og vurderer vi rollefordelingen mellom deltakerne, blir det enda flere kombinasjoner. ...jeg har veldig lyst, men jeg skal likevel avstå fra å fortsette for ikke å innpode deg en aversjon mot studentlivet =).

Regelen for å multiplisere kombinasjoner gjelder også for et større antall multiplikatorer:

Oppgave 8

Hvor mange tresifrede tall er det som er delbare med 5?

Løsning: for klarhetens skyld, la oss betegne dette nummeret med tre stjerner: ***

I hundrevis plass Du kan skrive hvilket som helst av tallene (1, 2, 3, 4, 5, 6, 7, 8 eller 9). Null er ikke egnet, siden tallet i dette tilfellet slutter å være tresifret.

Men i titalls plass("i midten") kan du velge hvilket som helst av 10 sifre: .

Ifølge betingelsen skal tallet være delelig med 5. Et tall er delbart med 5 hvis det ender på 5 eller 0. Dermed nøyer vi oss med 2 siffer i det minst signifikante sifferet.

Totalt er det: tresifrede tall som er delbare med 5.

I dette tilfellet er verket dechiffrert som følger: "9 måter du kan velge et tall på hundrevis plass Og 10 måter å velge et tall på titalls plass Og 2 veier inn enheter siffer»

Eller enda enklere: " Hver fra 9 sifre til hundrevis plass kombinerer med hver på 10 sifre titalls plass og med hver fra to sifre til enheter siffer».

Svar: 180

Og nå…

Ja, jeg glemte nesten den lovede kommentaren til problem nr. 5, der Bor, Dima og Volodya kan få utdelt ett kort hver på forskjellige måter. Multiplikasjon her har samme betydning: måter å fjerne 3 kort fra bunken OG i hver prøve omorganisere dem på måter.

Og nå et problem å løse på egen hånd... nå skal jeg finne på noe mer interessant... la det handle om den samme russiske versjonen av blackjack:

Oppgave 9

Hvor mange vinnende kombinasjoner av 2 kort er det når du spiller "poeng"?

For de som ikke vet: Vinnerkombinasjonen er 10 + ESS (11 poeng) = 21 poeng, og la oss vurdere den vinnende kombinasjonen av to ess.

(rekkefølgen på kortene i et par spiller ingen rolle)

En kort løsning og svar på slutten av timen.

Vurder forresten ikke eksemplet som primitivt. Blackjack er nesten det eneste spillet det finnes en matematisk basert algoritme for som lar deg slå kasinoet. De som er interessert kan enkelt finne et vell av informasjon om optimal strategi og taktikk. Riktignok havner slike mestere ganske raskt på svartelisten over alle bedrifter =)

Det er på tide å konsolidere materialet dekket med et par solide oppgaver:

Oppgave 10

Vasya har 4 katter hjemme.

a) på hvor mange måter kan katter sitte i hjørnene av rommet?
b) på hvor mange måter kan du la katter gå på tur?
c) på hvor mange måter kan Vasya plukke opp to katter (en på venstre side, den andre på høyre side)?

La oss bestemme: For det første bør du igjen ta hensyn til det faktum at problemet omhandler annerledes gjenstander (selv om kattene er eneggede tvillinger). Dette er en veldig viktig betingelse!

a) Stillhet av katter. Med forbehold om denne utførelsen alle kattene på en gang
+ deres plassering er viktig, så det er permutasjoner her:
ved hjelp av disse metodene kan du plassere katter i hjørnene av rommet.

Jeg gjentar at ved permutering er det bare antall forskjellige objekter og deres relative posisjoner som betyr noe. Avhengig av Vasyas humør, kan hun sette dyrene i en halvsirkel på sofaen, på rad i vinduskarmen, etc. – i alle tilfeller vil det være 24 permutasjoner.For enkelhets skyld kan interesserte forestille seg at katter er flerfargede (for eksempel hvit, svart, rød og tabby) og liste opp alle mulige kombinasjoner.

b) På hvor mange måter kan du la katter gå på tur?

Det antas at katter går turer bare gjennom døren, og spørsmålet innebærer likegyldighet angående antall dyr - 1, 2, 3 eller alle 4 kattene kan gå på tur.

Vi teller alle mulige kombinasjoner:

På en måte kan du la én katt (hvilken som helst av de fire) gå en tur;
måter du kan la to katter gå på tur (liste opp alternativene selv);
på måter du kan la tre katter gå på tur (en av de fire sitter hjemme);
På denne måten kan du slippe alle kattene.

Du har sannsynligvis gjettet at de resulterende verdiene burde oppsummeres:
måter du kan la katter gå på tur.

For entusiaster tilbyr jeg en komplisert versjon av problemet - når en hvilken som helst katt i en hvilken som helst prøve kan gå tilfeldig ut, både gjennom døren og gjennom vinduet i 10. etasje. Det vil være en merkbar økning i kombinasjoner!

c) På hvor mange måter kan Vasya plukke opp to katter?

Situasjonen innebærer ikke bare å velge 2 dyr, men også å plassere dem i hver hånd:
På disse måtene kan du plukke opp 2 katter.

Andre løsning: du kan velge to katter ved hjelp av metoder Og måter å plante på hver et par for hånden:

Svar: a) 24, b) 15, c) 12

Vel, for å rense samvittigheten, noe mer spesifikt om å multiplisere kombinasjoner... La Vasya få 5 ekstra katter =) På hvor mange måter kan du la 2 katter gå en tur? Og 1 katt?

Det vil si med Hver et par katter kan slippes løs hver katt.

Et annet knappetrekkspill for uavhengig løsning:

Oppgave 11

Tre passasjerer gikk om bord i heisen til en 12-etasjers bygning. Alle, uavhengig av de andre, kan gå ut i hvilken som helst (fra 2.) etasje med like stor sannsynlighet. På hvor mange måter:

1) passasjerer kan gå av i samme etasje (utgangsrekkefølge spiller ingen rolle);
2) to personer kan gå av i en etasje, og en tredje i den andre;
3) folk kan gå ut i forskjellige etasjer;
4) kan passasjerer gå ut av heisen?

Og her spør de ofte igjen, jeg presiserer: hvis 2 eller 3 personer går ut i samme etasje, spiller ikke rekkefølgen på utgangen noen rolle. TENK, bruk formler og regler for å legge til/multiplisere kombinasjoner. Ved vanskeligheter er det nyttig for passasjerene å oppgi navn og spekulere i hvilke kombinasjoner de kan gå ut av heisen. Det er ingen grunn til å bli opprørt hvis noe ikke fungerer, for eksempel er punkt nr. 2 ganske lumsk.

Full løsning med detaljerte kommentarer på slutten av leksjonen.

Det siste avsnittet er viet kombinasjoner som også forekommer ganske ofte - etter min subjektive vurdering, i omtrent 20-30 % av kombinatoriske problemer:

Permutasjoner, kombinasjoner og plasseringer med repetisjoner

De listede kombinasjonstypene er skissert i avsnitt nr. 5 i referansematerialet Grunnleggende formler for kombinatorikk, men noen av dem er kanskje ikke veldig klare ved første lesning. I dette tilfellet er det først tilrådelig å gjøre deg kjent med praktiske eksempler, og først da forstå den generelle formuleringen. Gå:

Permutasjoner med repetisjoner

I permutasjoner med repetisjoner, som i "vanlige" permutasjoner, alle de mange gjenstandene på en gang, men det er én ting: i dette settet gjentas ett eller flere elementer (objekter). Møt neste standard:

Oppgave 12

Hvor mange forskjellige bokstavkombinasjoner kan fås ved å omorganisere kort med følgende bokstaver: K, O, L, O, K, O, L, b, Ch, I, K?

Løsning: i tilfelle at alle bokstavene var forskjellige, bør en triviell formel brukes, men det er helt klart at for det foreslåtte settet med kort vil noen manipulasjoner fungere "tomt", for eksempel hvis du bytter to kort med bokstavene "K" " i et hvilket som helst ord, får du det samme ordet. Dessuten kan kortene fysisk være veldig forskjellige: det ene kan være rundt med bokstaven "K" trykt på det, det andre kan være firkantet med bokstaven "K" tegnet på. Men i henhold til betydningen av oppgaven, selv slike kort anses som de samme, siden betingelsen spør om bokstavkombinasjoner.

Alt er ekstremt enkelt - bare 11 kort, inkludert bokstaven:

K - gjentas 3 ganger;
O – gjentas 3 ganger;
L - gjentas 2 ganger;
b - gjentas 1 gang;
H – gjentas 1 gang;
Og - gjentas 1 gang.

Sjekk: 3 + 3 + 2 + 1 + 1 + 1 = 11, som er det som måtte sjekkes.

I henhold til formelen antall permutasjoner med repetisjoner:
forskjellige bokstavkombinasjoner kan fås. Mer enn en halv million!

For raskt å beregne en stor faktorverdi, er det praktisk å bruke standard Excel-funksjonen: skriv inn i hvilken som helst celle =FAKTA(11) og trykk Tast inn.

I praksis er det ganske akseptabelt å ikke skrive den generelle formelen og i tillegg utelate enhetsfaktorene:

Men det kreves foreløpige kommentarer om gjentatte brev!

Svar: 554400

Et annet typisk eksempel på permutasjoner med repetisjon forekommer i sjakkbrikkeplasseringsproblemet, som kan finnes på lageret ferdige løsninger i tilsvarende pdf. Og for en uavhengig løsning kom jeg på en mindre formel oppgave:

Oppgave 13

Alexey går inn for sport, og 4 dager i uken - friidrett, 2 dager - styrkeøvelser og 1 dag hvile. På hvor mange måter kan han lage en ukeplan for seg selv?

Formelen fungerer ikke her fordi den tar hensyn til tilfeldige bytter (for eksempel å bytte onsdagens styrkeøvelser med torsdagens styrkeøvelser). Og igjen - faktisk kan de samme 2 styrketreningsøktene være veldig forskjellige fra hverandre, men i sammenheng med oppgaven (fra planens synspunkt) anses de som de samme elementene.

To linjers løsning og svar på slutten av timen.

Kombinasjoner med repetisjoner

Et karakteristisk trekk ved denne typen kombinasjon er at prøven er trukket fra flere grupper, som hver består av identiske objekter.

Alle har jobbet hardt i dag, så det er på tide å friske opp deg selv:

Oppgave 14

Studentkantina selger pølser i deig, ostekaker og smultringer. På hvor mange måter kan du kjøpe fem paier?

Løsning: Vær umiddelbart oppmerksom på det typiske kriteriet for kombinasjoner med repetisjoner - i henhold til betingelsen er det ikke et sett med objekter som sådan som tilbys for valg, men forskjellige typer gjenstander; det antas at det er minst fem pølser, 5 ostekaker og 5 smultringer på salg. Paiene i hver gruppe er selvfølgelig forskjellige - fordi helt identiske smultringer bare kan simuleres på en datamaskin =) De fysiske egenskapene til paiene er imidlertid ikke signifikante for formålet med problemet, og pølsene / ostekakene / smultringer i gruppene deres anses som de samme.

Hva kan være i prøven? Først av alt bør det bemerkes at det definitivt vil være identiske paier i prøven (siden vi velger 5 stykker, og det er 3 typer å velge mellom). Det er alternativer her for enhver smak: 5 pølser, 5 ostekaker, 5 smultringer, 3 pølser + 2 ostekaker, 1 pølse + 2 ostekaker + 2 smultringer, etc.

Som med "vanlige" kombinasjoner, spiller rekkefølgen på utvalg og plassering av paier i utvalget ingen rolle - du valgte bare 5 stykker og det er det.

Vi bruker formelen antall kombinasjoner med repetisjoner:
Du kan kjøpe 5 paier ved å bruke denne metoden.

God appetitt!

Svar: 21

Hvilken konklusjon kan trekkes fra mange kombinatoriske problemer?

Noen ganger er det vanskeligste å forstå tilstanden.

Et lignende eksempel for en uavhengig løsning:

Oppgave 15

Lommeboken inneholder et ganske stort antall 1-, 2-, 5- og 10-rubelmynter. På hvor mange måter kan tre mynter fjernes fra en lommebok?

For selvkontrollformål, svar på et par enkle spørsmål:

1) Kan alle myntene i prøven være forskjellige?
2) Nevn den "billigste" og "dyreste" kombinasjonen av mynter.

Løsning og svar på slutten av timen.

Fra min personlige erfaring kan jeg si at kombinasjoner med repetisjoner er den sjeldneste gjesten i praksis, noe som ikke kan sies om følgende type kombinasjoner:

Plasseringer med repetisjoner

Fra et sett bestående av elementer velges elementer, og rekkefølgen på elementene i hvert utvalg er viktig. Og alt ville vært bra, men en ganske uventet vits er at vi kan velge et hvilket som helst objekt i originalsettet så mange ganger vi vil. Billedlig talt, "mengden vil ikke avta."

Når skjer dette? Et typisk eksempel er en kombinasjonslås med flere disker, men på grunn av teknologisk utvikling er det mer relevant å vurdere dens digitale etterkommer:

Oppgave 16

Hvor mange firesifrede PIN-koder er det?

Løsning: faktisk, for å løse problemet, er kunnskap om reglene for kombinatorikk nok: på måter kan du velge det første sifferet i PIN-koden Og måter - det andre sifferet i PIN-koden Og på like mange måter - tredje Og samme nummer - den fjerde. I henhold til regelen om å multiplisere kombinasjoner, kan en firesifret pin-kode være sammensatt på: måter.

Og nå bruker formelen. I henhold til betingelsen tilbys vi et sett med tall, hvorfra tallene velges og ordnes i en bestemt rekkefølge, mens tallene i prøven kan gjentas (dvs. ethvert siffer i originalsettet kan brukes et vilkårlig antall ganger). I henhold til formelen for antall plasseringer med repetisjoner:

Svar: 10000

Hva du tenker på her... ...hvis minibanken "spiser" kortet etter det tredje mislykkede forsøket på å taste inn PIN-koden, så er sjansen for å plukke den tilfeldig svært liten.

Og hvem sa at kombinatorikk ikke har noen praktisk betydning? En kognitiv oppgave for alle lesere av nettstedet:

Oppgave 17

I henhold til statens standard består et bilskilt av 3 tall og 3 bokstaver. I dette tilfellet er et tall med tre nuller uakseptabelt, og bokstaver er valgt fra settet A, B, E, K, M, N, O, P, S, T, U, X (bare de kyrilliske bokstavene brukes hvis stavemåte sammenfaller med latinske bokstaver).

Hvor mange forskjellige bilskilt kan opprettes for en region?

Ikke så mange av dem, forresten. I store regioner er det ikke nok slik mengde, og derfor er det flere koder for inskripsjonen RUS for dem.

Løsningen og svaret er på slutten av leksjonen. Ikke glem å bruke reglene for kombinatorikk ;-) ...Jeg ville vise frem det som var eksklusivt, men det viste seg ikke å være eksklusivt =) Jeg så på Wikipedia - det er beregninger der, men uten kommentarer. Selv om det sannsynligvis var for pedagogiske formål, var det få som løste det.

Vår spennende leksjon har nådd slutten, og til slutt vil jeg si at du ikke har kastet bort tiden din - av den grunn at kombinatoriske formler finner en annen viktig praktisk anvendelse: de finnes i forskjellige problemer i sannsynlighetsteori,
og i problemer som involverer klassisk sannsynlighetsbestemmelse– spesielt ofte =)

Takk alle sammen for deres aktive deltakelse og ses snart!

Løsninger og svar:

Oppgave 2: Løsning: finn antall mulige permutasjoner av 4 kort:

Når et kort med null plasseres på 1. plass, blir tallet tresifret, så disse kombinasjonene bør utelukkes. La null være på 1. plass, så kan de resterende 3 sifrene i de nedre sifrene omorganiseres på forskjellige måter.

Merk : fordi Siden det bare er noen få kort, er det enkelt å liste opp alle alternativene her:
0579
0597
0759
0795
0957
0975

Så fra det foreslåtte settet kan vi lage:
24 – 6 = 18 firesifrede tall
Svar : 18

Oppgave 4: Løsning: på måter kan du velge 3 kort av 36.
Svar : 7140

Oppgave 6: Løsning: måter.
En annen løsning : måter du kan velge to personer fra gruppen og og
2) Det "billigste" settet inneholder 3 rubelmynter, og det "dyreste" - 3 ti-rubelmynter.

Oppgave 17: Løsning: ved å bruke disse metodene kan du lage en digital kombinasjon av et bilnummer, mens en av dem (000) skal utelukkes: .
ved å bruke disse metodene kan du lage en bokstavkombinasjon av et nummerskilt.
I henhold til regelen om å multiplisere kombinasjoner, kan summen gjøres:
bilskilt
(Hver digital kombinasjon er kombinert med hver bokstavkombinasjon).
Svar : 1726272

La oss telle i MS EXCEL antall kombinasjoner av n elementer med k. Ved hjelp av formler vil vi vise på arket alle variantene av kombinasjoner (engelsk oversettelse av begrepet: Kombinasjoner uten repetisjon).

Kombinasjoner av n forskjellige elementer av k elementer er kombinasjoner som er forskjellige i minst ett element. Nedenfor er for eksempel ALLE 3-elementkombinasjoner hentet fra et sett bestående av 5 elementer (1; 2; 3; 4; 5):

(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)

Merk: Dette er en artikkel om å telle antall kombinasjoner med MS EXCEL. Vi anbefaler å lese det teoretiske grunnlaget i en spesialisert lærebok. Å lære kombinasjoner fra denne artikkelen er en dårlig idé.

Forskjellen mellom kombinasjoner og plasseringer

Viser alle kombinasjoner av kombinasjoner

I eksempelfilen lages formler for å vise alle kombinasjoner for gitte n og k.

Ved å spesifisere antall elementer i settet (n) og antall elementer som vi velger fra det (k), ved å bruke formler kan vi vise alle kombinasjoner.

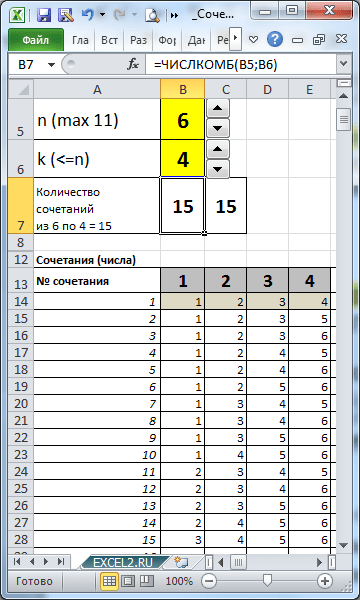
Oppgave

En biltransporter kan frakte 4 biler. Det er nødvendig å transportere 7 forskjellige biler (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). På hvor mange forskjellige måter kan den første biltransportøren fylles? Den spesifikke plasseringen av bilen i biltransporteren er ikke viktig.

Vi må bestemme antallet Kombinasjoner 7 biler på 4 plasser av en biltransporter. De. n=7 og k=4. Det viser seg at det er 35 slike alternativer =NUMCOMB(7,4).