How to solve ordinary fractions. How to solve examples with fractions
This article is a general look at operating with fractions. Here we will formulate and justify the rules for addition, subtraction, multiplication, division and exponentiation of fractions of the general form A/B, where A and B are some numbers, numerical expressions or expressions with variables. As usual, we will provide the material with explanatory examples with detailed descriptions of solutions.
Page navigation.
Rules for performing operations with general numerical fractions
Let's agree that by general numerical fractions we mean fractions in which the numerator and/or denominator can be represented not only by natural numbers, but also by other numbers or numerical expressions. For clarity, here are a few examples of such fractions: ,  .
.
We know the rules by which they are carried out. Using the same rules, you can perform operations with general fractions:
Rationale for the rules
To justify the validity of the rules for performing operations with numerical fractions of a general form, you can start from the following points:
- The slash is essentially a division sign,
- division by some nonzero number can be considered as multiplication by the inverse of the divisor (this immediately explains the rule for dividing fractions),
- properties of operations with real numbers,
- and its general understanding,
They allow you to carry out the following transformations that justify the rules of addition, subtraction of fractions with like and unlike denominators, as well as the rule of multiplication of fractions: 
Examples
Let us give examples of performing operations with general fractions according to the rules learned in the previous paragraph. Let's say right away that usually after performing operations with fractions, the resulting fraction requires simplification, and the process of simplifying a fraction is often more complicated than performing previous actions. We will not dwell in detail on simplifying fractions (the corresponding transformations are discussed in the article transforming fractions), so as not to be distracted from the topic that interests us.
Let's start with examples of adding and subtracting fractions with like denominators. First, let's add the fractions and . Obviously the denominators are equal. According to the corresponding rule, we write down a fraction whose numerator is equal to the sum of the numerators of the original fractions, and leave the denominator the same, we have. The addition is done, all that remains is to simplify the resulting fraction: ![]() . So,
. So, ![]() .
.
The solution could have been handled differently: first make the transition to ordinary fractions, and then carry out the addition. With this approach we have ![]() .
.
Now let's subtract from the fraction  fraction
fraction  . The denominators of the fractions are equal, therefore, we follow the rule for subtracting fractions with the same denominators:
. The denominators of the fractions are equal, therefore, we follow the rule for subtracting fractions with the same denominators: 
Let's move on to examples of adding and subtracting fractions with different denominators. The main difficulty here is bringing fractions to a common denominator. For general fractions, this is a rather extensive topic; we will examine it in detail in a separate article. bringing fractions to a common denominator. For now, we will limit ourselves to a couple of general recommendations, since at the moment we are more interested in the technique of performing operations with fractions.
In general, the process is similar to reducing ordinary fractions to a common denominator. That is, the denominators are presented in the form of products, then all the factors from the denominator of the first fraction are taken and the missing factors from the denominator of the second fraction are added to them.
When the denominators of fractions being added or subtracted do not have common factors, then it is logical to take their product as the common denominator. Let's give an example.
Let's say we need to perform addition of fractions and 1/2. Here, as a common denominator, it is logical to take the product of the denominators of the original fractions, that is, . In this case, the additional factor for the first fraction will be 2. After multiplying the numerator and denominator by it, the fraction will take the form . And for the second fraction, the additional factor is the expression. With its help, the fraction 1/2 is reduced to the form . All that remains is to add the resulting fractions with the same denominators. Here's a summary of the entire solution: 
In the case of general fractions, we are no longer talking about the lowest common denominator, to which ordinary fractions are usually reduced. Although in this matter it is still advisable to strive for some minimalism. By this we want to say that you should not immediately take the product of the denominators of the original fractions as a common denominator. For example, it is not at all necessary to take the common denominator of fractions and the product  . Here we can take .
. Here we can take .
Let's move on to examples of multiplying general fractions. Let's multiply fractions and . The rule for performing this action instructs us to write down a fraction, the numerator of which is the product of the numerators of the original fractions, and the denominator is the product of the denominators. We have  . Here, as in many other cases when multiplying fractions, you can reduce the fraction:
. Here, as in many other cases when multiplying fractions, you can reduce the fraction:  .
.
The rule for dividing fractions allows you to move from division to multiplication by the reciprocal fraction. Here you need to remember that in order to get the inverse of a given fraction, you need to swap the numerator and denominator of the given fraction. Here is an example of the transition from division of general numerical fractions to multiplication:  . All that remains is to perform the multiplication and simplify the resulting fraction (if necessary, see the transformation of irrational expressions):
. All that remains is to perform the multiplication and simplify the resulting fraction (if necessary, see the transformation of irrational expressions): 
Concluding the information in this paragraph, recall that any number or numerical expression can be represented as a fraction with a denominator 1, therefore, addition, subtraction, multiplication and division of numbers and fractions can be considered as performing the corresponding operation with fractions, one of which has one in the denominator . For example, replacing in the expression  root of three by a fraction, we move from multiplying a fraction by a number to multiplying two fractions:
root of three by a fraction, we move from multiplying a fraction by a number to multiplying two fractions:  .
.
Doing things with fractions that contain variables
The rules from the first part of this article also apply to performing operations with fractions that contain variables. Let's justify the first of them - the rule for adding and subtracting fractions with identical denominators, the rest are proven in absolutely the same way.
Let us prove that for any expressions A, C and D (D is not identically equal to zero) the equality holds ![]() on its range of permissible values of variables.
on its range of permissible values of variables.
Let's take a certain set of variables from the ODZ. Let the expressions A, C and D take the values a 0, c 0 and d 0 for these values of the variables. Then substituting the values of variables from the selected set into the expression turns it into a sum (difference) of numerical fractions with like denominators of the form , which, according to the rule of addition (subtraction) of numerical fractions with like denominators, is equal to . But substituting the values of variables from the selected set into the expression turns it into the same fraction. This means that for the selected set of variable values from the ODZ, the values of the expressions and are equal. It is clear that the values of the indicated expressions will be equal for any other set of values of variables from the ODZ, which means that the expressions and are identically equal, that is, the equality being proved is true ![]() .
.
Examples of adding and subtracting fractions with variables
When the denominators of the fractions being added or subtracted are the same, then everything is quite simple - the numerators are added or subtracted, but the denominator remains the same. It is clear that the fraction obtained after this is simplified if necessary and possible.
Note that sometimes the denominators of fractions differ only at first glance, but in fact they are identically equal expressions, for example,  and , or and . And sometimes it is enough to simplify the original fractions so that their identical denominators “appear.”
and , or and . And sometimes it is enough to simplify the original fractions so that their identical denominators “appear.”
Example.
 , b)
, b)  , V)
, V)  .
.
Solution.
a) We need to subtract fractions with like denominators. According to the corresponding rule, we leave the denominator the same and subtract the numerators, we have  . The action has been completed. But you can also open the parentheses in the numerator and present similar terms:
. The action has been completed. But you can also open the parentheses in the numerator and present similar terms:  .
.
b) Obviously, the denominators of the fractions being added are the same. Therefore, we add up the numerators and leave the denominator the same: . Addition completed. But it is easy to see that the resulting fraction can be reduced. Indeed, the numerator of the resulting fraction can be collapsed using the formula square of the sum as (lgx+2) 2 (see formulas for abbreviated multiplication), thus the following transformations take place:  .
.
c) Fractions in sum  have different denominators. But, having transformed one of the fractions, you can move on to adding fractions with the same denominators. We will show two solutions.
have different denominators. But, having transformed one of the fractions, you can move on to adding fractions with the same denominators. We will show two solutions.
First way. The denominator of the first fraction can be factorized using the difference of squares formula, and then reduce this fraction:  . Thus, . It still doesn’t hurt to free yourself from irrationality in the denominator of the fraction:
. Thus, . It still doesn’t hurt to free yourself from irrationality in the denominator of the fraction:  .
.
Second way. Multiplying the numerator and denominator of the second fraction by (this expression does not go to zero for any value of the variable x from the ODZ for the original expression) allows you to achieve two goals at once: free yourself from irrationality and move on to adding fractions with the same denominators. We have 
Answer:
A)  , b)
, b)  , V)
, V)  .
.
The last example brought us to the question of reducing fractions to a common denominator. There we almost accidentally arrived at the same denominators by simplifying one of the added fractions. But in most cases, when adding and subtracting fractions with different denominators, you have to purposefully bring the fractions to a common denominator. To do this, usually the denominators of fractions are presented in the form of products, all the factors from the denominator of the first fraction are taken and the missing factors from the denominator of the second fraction are added to them.
Example.
Perform operations with fractions: a)  , b) , c)
, b) , c)  .
.
Solution.
a) There is no need to do anything with the denominators of the fractions. As a common denominator we take the product ![]() . In this case, the additional factor for the first fraction is the expression, and for the second fraction - the number 3. These additional factors bring the fractions to a common denominator, which later allows us to perform the action we need, we have
. In this case, the additional factor for the first fraction is the expression, and for the second fraction - the number 3. These additional factors bring the fractions to a common denominator, which later allows us to perform the action we need, we have 
b) In this example, the denominators are already represented as products and do not require any additional transformations. Obviously, the factors in the denominators differ only in exponents, therefore, as a common denominator we take the product of the factors with the highest exponents, that is, ![]() . Then the additional factor for the first fraction will be x 4, and for the second – ln(x+1) . Now we're ready to subtract fractions:
. Then the additional factor for the first fraction will be x 4, and for the second – ln(x+1) . Now we're ready to subtract fractions: 
c) And in this case, first we will work with the denominators of fractions. The formulas for the difference of squares and the square of the sum allow you to move from the original sum to the expression  . Now it is clear that these fractions can be reduced to a common denominator
. Now it is clear that these fractions can be reduced to a common denominator ![]() . With this approach, the solution will look like this:
. With this approach, the solution will look like this: 
Answer:
A) 
b) 
V) 
Examples of multiplying fractions with variables
Multiplying fractions produces a fraction whose numerator is the product of the numerators of the original fractions, and the denominator is the product of the denominators. Here, as you can see, everything is familiar and simple, and we can only add that the fraction obtained as a result of this action often turns out to be reducible. In these cases, it is reduced, unless, of course, it is necessary and justified.
Fractions
Attention!
There are additional
materials in Special Section 555.
For those who are very "not very..."
And for those who “very much…”)
Fractions are not much of a nuisance in high school. For the time being. Until you come across powers with rational exponents and logarithms. And there... You press and press the calculator, and it shows a full display of some numbers. You have to think with your head like in the third grade.
Let's finally figure out fractions! Well, how much can you get confused in them!? Moreover, it’s all simple and logical. So, what are the types of fractions?
Types of fractions. Transformations.
There are three types of fractions.
1. Common fractions , For example:
Sometimes instead of a horizontal line they put a slash: 1/2, 3/4, 19/5, well, and so on. Here we will often use this spelling. The top number is called numerator, lower - denominator. If you constantly confuse these names (it happens...), say to yourself the phrase: " Zzzzz remember! Zzzzz denominator - look zzzzz uh!" Look, everything will be zzzz remembered.)
The dash, either horizontal or inclined, means division the top number (numerator) to the bottom (denominator). That's all! Instead of a dash, it is quite possible to put a division sign - two dots.
When complete division is possible, this must be done. So, instead of the fraction “32/8” it is much more pleasant to write the number “4”. Those. 32 is simply divided by 8.
32/8 = 32: 8 = 4
I'm not even talking about the fraction "4/1". Which is also just "4". And if it’s not completely divisible, we leave it as a fraction. Sometimes you have to do the opposite operation. Convert a whole number into a fraction. But more on that later.
2. Decimals , For example:
It is in this form that you will need to write down the answers to tasks “B”.
3. Mixed numbers , For example:
Mixed numbers are practically not used in high school. In order to work with them, they must be converted into ordinary fractions. But you definitely need to be able to do this! Otherwise you will come across such a number in a problem and freeze... Out of nowhere. But we will remember this procedure! A little lower.
Most versatile common fractions. Let's start with them. By the way, if a fraction contains all sorts of logarithms, sines and other letters, this does not change anything. In the sense that everything actions with fractional expressions are no different from actions with ordinary fractions!
The main property of a fraction.
So, let's go! To begin with, I will surprise you. The whole variety of fraction transformations is provided by one single property! That's what it's called main property of a fraction. Remember: If the numerator and denominator of a fraction are multiplied (divided) by the same number, the fraction does not change. Those:
It is clear that you can continue to write until you are blue in the face. Don’t let sines and logarithms confuse you, we’ll deal with them further. The main thing is to understand that all these various expressions are the same fraction . 2/3.
Do we need it, all these transformations? And how! Now you will see for yourself. To begin with, let's use the basic property of a fraction for reducing fractions. It would seem like an elementary thing. Divide the numerator and denominator by the same number and that's it! It's impossible to make a mistake! But... man is a creative being. You can make a mistake anywhere! Especially if you have to reduce not a fraction like 5/10, but a fractional expression with all sorts of letters.
How to correctly and quickly reduce fractions without doing extra work can be read in the special Section 555.
A normal student doesn't bother dividing the numerator and denominator by the same number (or expression)! He simply crosses out everything that is the same above and below! This is where a typical mistake, a blunder, if you will, lurks.
For example, you need to simplify the expression:
There’s nothing to think about here, cross out the letter “a” on top and the two on the bottom! We get:
Everything is correct. But really you divided all numerator and all the denominator is "a". If you are used to just crossing out, then in a hurry you can cross out the “a” in the expression
and get it again
Which would be categorically untrue. Because here all the numerator on "a" is already not shared! This fraction cannot be reduced. By the way, such a reduction is, um... a serious challenge for the teacher. This is not forgiven! Do you remember? When reducing, you need to divide all numerator and all denominator!
Reducing fractions makes life a lot easier. You will get a fraction somewhere, for example 375/1000. How can I continue to work with her now? Without a calculator? Multiply, say, add, square!? And if you’re not too lazy, and carefully cut it down by five, and by another five, and even... while it’s being shortened, in short. Let's get 3/8! Much nicer, right?
The main property of a fraction allows you to convert ordinary fractions to decimals and vice versa without a calculator! This is important for the Unified State Exam, right?
How to convert fractions from one type to another.
With decimal fractions everything is simple. As it is heard, so it is written! Let's say 0.25. This is zero point twenty five hundredths. So we write: 25/100. We reduce (we divide the numerator and denominator by 25), we get the usual fraction: 1/4. All. It happens, and nothing is reduced. Like 0.3. This is three tenths, i.e. 3/10.
What if the integers are not zero? It's OK. We write down the whole fraction without any commas in the numerator, and in the denominator - what is heard. For example: 3.17. This is three point seventeen hundredths. We write 317 in the numerator and 100 in the denominator. We get 317/100. Nothing is reduced, that means everything. This is the answer. Elementary Watson! From all that has been said, a useful conclusion: any decimal fraction can be converted to a common fraction .
But some people cannot do the reverse conversion from ordinary to decimal without a calculator. And it is necessary! How will you write down the answer on the Unified State Exam!? Read carefully and master this process.
What is the characteristic of a decimal fraction? Her denominator is Always costs 10, or 100, or 1000, or 10000 and so on. If your common fraction has a denominator like this, there's no problem. For example, 4/10 = 0.4. Or 7/100 = 0.07. Or 12/10 = 1.2. What if the answer to the task in section “B” turned out to be 1/2? What will we write in response? Decimals are required...
Let's remember main property of a fraction ! Mathematics favorably allows you to multiply the numerator and denominator by the same number. Anything, by the way! Except zero, of course. So let’s use this property to our advantage! What can the denominator be multiplied by, i.e. 2 so that it becomes 10, or 100, or 1000 (smaller is better, of course...)? At 5, obviously. Feel free to multiply the denominator (this is us necessary) by 5. But then the numerator must also be multiplied by 5. This is already mathematics demands! We get 1/2 = 1x5/2x5 = 5/10 = 0.5. That's all.
However, all sorts of denominators come across. You will come across, for example, the fraction 3/16. Try and figure out what to multiply 16 by to make 100, or 1000... Doesn’t it work? Then you can simply divide 3 by 16. In the absence of a calculator, you will have to divide with a corner, on a piece of paper, as they taught in elementary school. We get 0.1875.
And there are also very bad denominators. For example, there is no way to turn the fraction 1/3 into a good decimal. Both on the calculator and on a piece of paper, we get 0.3333333... This means that 1/3 is an exact decimal fraction does not translate. Same as 1/7, 5/6 and so on. There are many of them, untranslatable. This brings us to another useful conclusion. Not every fraction can be converted to a decimal !
By the way, this is useful information for self-testing. In section "B" you must write down a decimal fraction in your answer. And you got, for example, 4/3. This fraction does not convert to a decimal. This means you made a mistake somewhere along the way! Go back and check the solution.
So, we figured out ordinary and decimal fractions. All that remains is to deal with mixed numbers. To work with them, they must be converted into ordinary fractions. How to do it? You can catch a sixth grader and ask him. But a sixth grader won’t always be at hand... You’ll have to do it yourself. It is not difficult. You need to multiply the denominator of the fractional part by the whole part and add the numerator of the fractional part. This will be the numerator of the common fraction. What about the denominator? The denominator will remain the same. It sounds complicated, but in reality everything is simple. Let's look at an example.
Suppose you were horrified to see the number in the problem:
Calmly, without panic, we think. The whole part is 1. Unit. The fractional part is 3/7. Therefore, the denominator of the fractional part is 7. This denominator will be the denominator of the ordinary fraction. We count the numerator. We multiply 7 by 1 (the integer part) and add 3 (the numerator of the fractional part). We get 10. This will be the numerator of a common fraction. That's all. It looks even simpler in mathematical notation:

Is it clear? Then secure your success! Convert to ordinary fractions. You should get 10/7, 7/2, 23/10 and 21/4.
The reverse operation - converting an improper fraction to a mixed number - is rarely required in high school. Well, if so... And if you are not in high school, you can look into the special Section 555. By the way, you will also learn about improper fractions there.
Well, that's practically all. You remembered the types of fractions and understood How transfer them from one type to another. The question remains: For what do it? Where and when to apply this deep knowledge?
I answer. Any example itself suggests the necessary actions. If in the example ordinary fractions, decimals, and even mixed numbers are mixed together, we convert everything into ordinary fractions. It can always be done. Well, if it says something like 0.8 + 0.3, then we count it that way, without any translation. Why do we need extra work? We choose the solution that is convenient us !
If the task is all decimal fractions, but um... some kind of evil ones, go to ordinary ones and try it! Look, everything will work out. For example, you will have to square the number 0.125. It’s not so easy if you haven’t gotten used to using a calculator! Not only do you have to multiply numbers in a column, you also have to think about where to insert the comma! It definitely won’t work in your head! What if we move on to an ordinary fraction?
0.125 = 125/1000. We reduce it by 5 (this is for starters). We get 25/200. Once again by 5. We get 5/40. Oh, it's still shrinking! Back to 5! We get 1/8. We can easily square it (in our minds!) and get 1/64. All!
Let's summarize this lesson.
1. There are three types of fractions. Common, decimal and mixed numbers.
2. Decimals and mixed numbers Always can be converted to ordinary fractions. Reverse transfer not always available.
3. The choice of the type of fractions to work with a task depends on the task itself. If there are different types of fractions in one task, the most reliable thing is to switch to ordinary fractions.
Now you can practice. First, convert these decimal fractions to ordinary fractions:
3,8; 0,75; 0,15; 1,4; 0,725; 0,012
You should get answers like this (in a mess!):
Let's finish here. In this lesson we refreshed our memory on key points about fractions. It happens, however, that there is nothing special to refresh...) If someone has completely forgotten, or has not yet mastered it... Then you can go to a special Section 555. All the basics are covered in detail there. Many suddenly understand everything are starting. And they solve fractions on the fly).
If you like this site...
By the way, I have a couple more interesting sites for you.)
You can practice solving examples and find out your level. Testing with instant verification. Let's learn - with interest!)
You can get acquainted with functions and derivatives.
To express a part as a fraction of the whole, you need to divide the part into the whole.
Task 1. There are 30 students in the class, four are absent. What proportion of students are absent?
Solution:
Answer: There are no students in the class.
Finding a fraction from a number
To solve problems in which you need to find a part of a whole, the following rule applies:
If a part of a whole is expressed as a fraction, then to find this part, you can divide the whole by the denominator of the fraction and multiply the result by its numerator.
Task 1. There were 600 rubles, this amount was spent. How much money did you spend?
Solution: to find 600 rubles or more, we need to divide this amount into 4 parts, thereby we will find out how much money one fourth part is:
600: 4 = 150 (r.)
Answer: spent 150 rubles.
Task 2. There were 1000 rubles, this amount was spent. How much money was spent?
Solution: from the problem statement we know that 1000 rubles consists of five equal parts. First, let’s find how many rubles are one-fifth of 1000, and then we’ll find out how many rubles are two-fifths:
1) 1000: 5 = 200 (r.) - one fifth.
2) 200 · 2 = 400 (r.) - two fifths.
These two actions can be combined: 1000: 5 · 2 = 400 (r.).
Answer: 400 rubles were spent.
The second way to find a part of a whole:
To find a part of a whole, you can multiply the whole by the fraction expressing that part of the whole.
Task 3. According to the charter of the cooperative, for the reporting meeting to be valid, at least at least members of the organization must be present. The cooperative has 120 members. What composition can a reporting meeting take place?
Solution: ![]()
Answer: the reporting meeting can take place if there are 80 members of the organization.
Finding a number by its fraction
To solve problems in which you need to find a whole from its part, the following rule applies:
If part of the desired whole is expressed as a fraction, then to find this whole, you can divide this part by the numerator of the fraction and multiply the result by its denominator.
Task 1. We spent 50 rubles, which was less than the original amount. Find the original amount of money.
Solution: from the description of the problem we see that 50 rubles is 6 times less than the original amount, i.e. the original amount is 6 times more than 50 rubles. To find this amount, you need to multiply 50 by 6:
50 · 6 = 300 (r.)
Answer: the initial amount is 300 rubles.
Task 2. We spent 600 rubles, which was less than the original amount of money. Find the original amount.
Solution: We will assume that the required number consists of three thirds. According to the condition, two-thirds of the number equals 600 rubles. First, let's find one third of the original amount, and then how many rubles are three thirds (the original amount):
1) 600: 2 3 = 900 (r.)
Answer: the initial amount is 900 rubles.
The second way to find a whole from its part:
To find a whole by the value expressing its part, you can divide this value by the fraction expressing this part.
Task 3. Line segment AB, equal to 42 cm, is the length of the segment CD. Find the length of the segment CD.
Solution: ![]()
Answer: segment length CD 70 cm.
Task 4. Watermelons were brought to the store. Before lunch, the store sold the watermelons it brought, and after lunch, there were 80 watermelons left to sell. How many watermelons did you bring to the store?
Solution: First, let’s find out what part of the brought watermelons is the number 80. To do this, let’s take the total number of watermelons brought as one and subtract from it the number of watermelons that were sold (sold):
And so, we learned that 80 watermelons make up the total number of watermelons brought. Now we find out how many watermelons from the total amount make up, and then how many watermelons make up (the number of watermelons brought):
2) 80: 4 15 = 300 (watermelons)
Answer: In total, 300 watermelons were brought to the store.
This section covers operations with ordinary fractions. If it is necessary to carry out a mathematical operation with mixed numbers, then it is enough to convert the mixed fraction into an extraordinary fraction, carry out the necessary operations and, if necessary, present the final result again in the form of a mixed number. This operation will be described below.
Reducing a fraction
Mathematical operation. Reducing a fraction
To reduce the fraction \frac(m)(n) you need to find the greatest common divisor of its numerator and denominator: gcd(m,n), and then divide the numerator and denominator of the fraction by this number. If GCD(m,n)=1, then the fraction cannot be reduced. Example: \frac(20)(80)=\frac(20:20)(80:20)=\frac(1)(4)
Usually, immediately finding the greatest common divisor seems to be a difficult task, and in practice, a fraction is reduced in several stages, step by step isolating obvious common factors from the numerator and denominator. \frac(140)(315)=\frac(28\cdot5)(63\cdot5)=\frac(4\cdot7\cdot5)(9\cdot7\cdot5)=\frac(4)(9)
Reducing fractions to a common denominator
Mathematical operation. Reducing fractions to a common denominator
To bring two fractions \frac(a)(b) and \frac(c)(d) to a common denominator you need:
- find the least common multiple of the denominators: M=LMK(b,d);
- multiply the numerator and denominator of the first fraction by M/b (after which the denominator of the fraction becomes equal to the number M);
- multiply the numerator and denominator of the second fraction by M/d (after which the denominator of the fraction becomes equal to the number M).
Thus, we transform the original fractions to fractions with the same denominators (which will be equal to the number M).
For example, the fractions \frac(5)(6) and \frac(4)(9) have LCM(6,9) = 18. Then: \frac(5)(6)=\frac(5\cdot3)(6 \cdot3)=\frac(15)(18);\quad\frac(4)(9)=\frac(4\cdot2)(9\cdot2)=\frac(8)(18) . Thus, the resulting fractions have a common denominator.
In practice, finding the least common multiple (LCM) of denominators is not always a simple task. Therefore, a number equal to the product of the denominators of the original fractions is chosen as the common denominator. For example, the fractions \frac(5)(6) and \frac(4)(9) are reduced to a common denominator N=6\cdot9:
\frac(5)(6)=\frac(5\cdot9)(6\cdot9)=\frac(45)(54);\quad\frac(4)(9)=\frac(4\cdot6)( 9\cdot6)=\frac(24)(54)
Comparison of fractions
Mathematical operation. Comparison of fractions
To compare two ordinary fractions you need:
- compare the numerators of the resulting fractions; a fraction with a larger numerator will be larger.
When comparing fractions, there are several special cases:
- From two fractions with the same denominators The fraction whose numerator is greater is greater. For example, \frac(3)(15)
- From two fractions with the same numerators The larger is the fraction whose denominator is smaller. For example, \frac(4)(11)>\frac(4)(13)
- That fraction which simultaneously larger numerator and smaller denominator, more. For example, \frac(11)(3)>\frac(10)(8)
Attention! Rule 1 applies to any fractions if their common denominator is a positive number. Rules 2 and 3 apply to positive fractions (those with both the numerator and denominator greater than zero).
Adding and subtracting fractions
Mathematical operation. Adding and subtracting fractions
To add two fractions you need:
- bring them to a common denominator;
- add their numerators and leave the denominator unchanged.
Example: \frac(7)(9)+\frac(4)(7)=\frac(7\cdot7)(9\cdot7)+\frac(4\cdot9)(7\cdot9)=\frac(49 )(63)+\frac(36)(63)=\frac(49+36)(63)=\frac(85)(63)
To subtract another from one fraction, you need:
- reduce fractions to a common denominator;
- Subtract the numerator of the second fraction from the numerator of the first fraction and leave the denominator unchanged.
Example: \frac(4)(15)-\frac(3)(5)=\frac(4)(15)-\frac(3\cdot3)(5\cdot3)=\frac(4)(15) -\frac(9)(15)=\frac(4-9)(15)=\frac(-5)(15)=-\frac(5)(3\cdot5)=-\frac(1)( 3)
If the original fractions initially have a common denominator, then step 1 (reduction to a common denominator) is skipped.
Converting a mixed number to an improper fraction and vice versa
Mathematical operation. Converting a mixed number to an improper fraction and vice versa
To convert a mixed fraction to an improper fraction, simply sum the whole part of the mixed fraction with the fraction part. The result of such a sum will be an improper fraction, the numerator of which is equal to the sum of the product of the whole part by the denominator of the fraction with the numerator of the mixed fraction, and the denominator will remain the same. For example, 2\frac(6)(11)=2+\frac(6)(11)=\frac(2\cdot11)(11)+\frac(6)(11)=\frac(2\cdot11+ 6)(11)=\frac(28)(11)
To convert an improper fraction to a mixed number:
- divide the numerator of a fraction by its denominator;
- write the remainder of the division into the numerator and leave the denominator the same;
- write the result of the division as an integer part.
For example, the fraction \frac(23)(4) . When dividing 23:4=5.75, that is, the whole part is 5, the remainder of the division is 23-5*4=3. Then the mixed number will be written: 5\frac(3)(4) . \frac(23)(4)=\frac(5\cdot4+3)(4)=5\frac(3)(4)
Converting a Decimal to a Fraction
Mathematical operation. Converting a Decimal to a Fraction
In order to convert a decimal fraction to a common fraction, you need to:
- take the nth power of ten as the denominator (here n is the number of decimal places);
- as the numerator, take the number after the decimal point (if the integer part of the original number is not equal to zero, then take all the leading zeros as well);
- the non-zero integer part is written in the numerator at the very beginning; the zero integer part is omitted.
Example 1: 0.0089=\frac(89)(10000) (there are 4 decimal places, so the denominator has 10 4 =10000, since the integer part is 0, the numerator contains the number after the decimal point without leading zeros)
Example 2: 31.0109=\frac(310109)(10000) (in the numerator we write the number after the decimal point with all zeros: “0109”, and then before it we add the whole part of the original number “31”)
If the whole part of a decimal fraction is non-zero, then it can be converted to a mixed fraction. To do this, we convert the number into an ordinary fraction as if the whole part were equal to zero (points 1 and 2), and simply rewrite the whole part in front of the fraction - this will be the whole part of the mixed number. Example:
3.014=3\frac(14)(100)
To convert a fraction to a decimal, simply divide the numerator by the denominator. Sometimes you end up with an infinite decimal. In this case, it is necessary to round to the desired decimal place. Examples:
\frac(401)(5)=80.2;\quad \frac(2)(3)\approx0.6667
Multiplying and dividing fractions
Mathematical operation. Multiplying and dividing fractions
To multiply two ordinary fractions, you need to multiply the numerators and denominators of the fractions.
\frac(5)(9)\cdot\frac(7)(2)=\frac(5\cdot7)(9\cdot2)=\frac(35)(18)
To divide one common fraction by another, you need to multiply the first fraction by the reciprocal of the second ( reciprocal fraction- a fraction in which the numerator and denominator are swapped.
\frac(5)(9):\frac(7)(2)=\frac(5)(9)\cdot\frac(2)(7)=\frac(5\cdot2)(9\cdot7)= \frac(10)(63)
If one of the fractions is a natural number, then the above rules of multiplication and division remain in force. You just need to take into account that an integer is the same fraction, the denominator of which is equal to one. For example: 3:\frac(3)(7)=\frac(3)(1):\frac(3)(7)=\frac(3)(1)\cdot\frac(7)(3)= \frac(3\cdot7)(1\cdot3)=\frac(7)(1)=7
Lesson contentAdding fractions with like denominators
There are two types of addition of fractions:
- Adding fractions with like denominators
- Adding fractions with different denominators
First, let's learn the addition of fractions with like denominators. Everything is simple here. To add fractions with the same denominators, you need to add their numerators and leave the denominator unchanged. For example, let's add the fractions and . Add the numerators and leave the denominator unchanged:

This example can be easily understood if we remember the pizza, which is divided into four parts. If you add pizza to pizza, you get pizza:

Example 2. Add fractions and .

The answer turned out to be an improper fraction. When the end of the task comes, it is customary to get rid of improper fractions. To get rid of an improper fraction, you need to select the whole part of it. In our case, the whole part is easily isolated - two divided by two equals one:

This example can be easily understood if we remember about a pizza that is divided into two parts. If you add more pizza to the pizza, you get one whole pizza:

Example 3. Add fractions and .
Again, we add up the numerators and leave the denominator unchanged:
![]()
This example can be easily understood if we remember the pizza, which is divided into three parts. If you add more pizza to the pizza, you get pizza:

Example 4. Find the value of an expression 
This example is solved in exactly the same way as the previous ones. The numerators must be added and the denominator left unchanged:
Let's try to depict our solution using a drawing. If you add pizzas to a pizza and add more pizzas, you get 1 whole pizza and more pizzas.

As you can see, there is nothing complicated about adding fractions with the same denominators. It is enough to understand the following rules:
- To add fractions with the same denominator, you need to add their numerators and leave the denominator unchanged;
Adding fractions with different denominators
Now let's learn how to add fractions with different denominators. When adding fractions, the denominators of the fractions must be the same. But they are not always the same.
For example, fractions can be added because they have the same denominators.
But fractions cannot be added right away, since these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.
There are several ways to reduce fractions to the same denominator. Today we will look at only one of them, since the other methods may seem complicated for a beginner.
The essence of this method is that first the LCM of the denominators of both fractions is searched. The LCM is then divided by the denominator of the first fraction to obtain the first additional factor. They do the same with the second fraction - the LCM is divided by the denominator of the second fraction and a second additional factor is obtained.
The numerators and denominators of the fractions are then multiplied by their additional factors. As a result of these actions, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to add such fractions.
Example 1. Let's add the fractions and
First of all, we find the least common multiple of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 2. The least common multiple of these numbers is 6
LCM (2 and 3) = 6
Now let's return to fractions and . First, divide the LCM by the denominator of the first fraction and get the first additional factor. LCM is the number 6, and the denominator of the first fraction is the number 3. Divide 6 by 3, we get 2.
The resulting number 2 is the first additional multiplier. We write it down to the first fraction. To do this, make a small oblique line over the fraction and write down the additional factor found above it:
We do the same with the second fraction. We divide the LCM by the denominator of the second fraction and get the second additional factor. LCM is the number 6, and the denominator of the second fraction is the number 2. Divide 6 by 2, we get 3.
The resulting number 3 is the second additional multiplier. We write it down to the second fraction. Again, we make a small oblique line over the second fraction and write down the additional factor found above it:
Now we have everything ready for addition. It remains to multiply the numerators and denominators of the fractions by their additional factors:

Look carefully at what we have come to. We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to add such fractions. Let's take this example to the end:

This completes the example. It turns out to add .
Let's try to depict our solution using a drawing. If you add pizza to a pizza, you get one whole pizza and another sixth of a pizza:

Reducing fractions to the same (common) denominator can also be depicted using a picture. Reducing the fractions and to a common denominator, we got the fractions and . These two fractions will be represented by the same pieces of pizza. The only difference will be that this time they will be divided into equal shares (reduced to the same denominator).

The first drawing represents a fraction (four pieces out of six), and the second drawing represents a fraction (three pieces out of six). Adding these pieces we get (seven pieces out of six). This fraction is improper, so we highlighted the whole part of it. As a result, we got (one whole pizza and another sixth pizza).
Please note that we have described this example in too much detail. In educational institutions it is not customary to write in such detail. You need to be able to quickly find the LCM of both denominators and additional factors to them, as well as quickly multiply the found additional factors by your numerators and denominators. If we were at school, we would have to write this example as follows:

But there is also another side to the coin. If you do not take detailed notes in the first stages of studying mathematics, then questions of the sort begin to appear. “Where does that number come from?”, “Why do fractions suddenly turn into completely different fractions? «.
To make it easier to add fractions with different denominators, you can use the following step-by-step instructions:
- Find the LCM of the denominators of fractions;
- Divide the LCM by the denominator of each fraction and obtain an additional factor for each fraction;
- Multiply the numerators and denominators of fractions by their additional factors;
- Add fractions that have the same denominators;
- If the answer turns out to be an improper fraction, then select its whole part;
Example 2. Find the value of an expression  .
.
Let's use the instructions given above.
Step 1. Find the LCM of the denominators of the fractions
Find the LCM of the denominators of both fractions. The denominators of fractions are the numbers 2, 3 and 4

Step 2. Divide the LCM by the denominator of each fraction and get an additional factor for each fraction
Divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 2. Divide 12 by 2, we get 6. We got the first additional factor 6. We write it above the first fraction:
Now we divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 3. Divide 12 by 3, we get 4. We get the second additional factor 4. We write it above the second fraction:
Now we divide the LCM by the denominator of the third fraction. LCM is the number 12, and the denominator of the third fraction is the number 4. Divide 12 by 4, we get 3. We get the third additional factor 3. We write it above the third fraction:
Step 3. Multiply the numerators and denominators of the fractions by their additional factors
We multiply the numerators and denominators by their additional factors:
Step 4. Add fractions with the same denominators
We came to the conclusion that fractions that had different denominators turned into fractions that had the same (common) denominators. All that remains is to add these fractions. Add it up:

The addition didn't fit on one line, so we moved the remaining expression to the next line. This is allowed in mathematics. When an expression does not fit on one line, it is moved to the next line, and it is necessary to put an equal sign (=) at the end of the first line and at the beginning of the new line. The equal sign on the second line indicates that this is a continuation of the expression that was on the first line.
Step 5. If the answer turns out to be an improper fraction, then select the whole part of it
Our answer turned out to be an improper fraction. We have to highlight a whole part of it. We highlight:

We received an answer
Subtracting fractions with like denominators
There are two types of subtraction of fractions:
- Subtracting fractions with like denominators
- Subtracting fractions with different denominators
First, let's learn how to subtract fractions with like denominators. Everything is simple here. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, but leave the denominator the same.
For example, let's find the value of the expression . To solve this example, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged. Let's do this:

This example can be easily understood if we remember the pizza, which is divided into four parts. If you cut pizzas from a pizza, you get pizzas:

Example 2. Find the value of the expression.
Again, from the numerator of the first fraction, subtract the numerator of the second fraction, and leave the denominator unchanged:

This example can be easily understood if we remember the pizza, which is divided into three parts. If you cut pizzas from a pizza, you get pizzas:

Example 3. Find the value of an expression 
This example is solved in exactly the same way as the previous ones. From the numerator of the first fraction you need to subtract the numerators of the remaining fractions:

As you can see, there is nothing complicated about subtracting fractions with the same denominators. It is enough to understand the following rules:
- To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged;
- If the answer turns out to be an improper fraction, then you need to highlight the whole part of it.
Subtracting fractions with different denominators
For example, you can subtract a fraction from a fraction because the fractions have the same denominators. But you cannot subtract a fraction from a fraction, since these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.
The common denominator is found using the same principle that we used when adding fractions with different denominators. First of all, find the LCM of the denominators of both fractions. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained, which is written above the first fraction. Similarly, the LCM is divided by the denominator of the second fraction and a second additional factor is obtained, which is written above the second fraction.
The fractions are then multiplied by their additional factors. As a result of these operations, fractions that had different denominators are converted into fractions that have the same denominators. And we already know how to subtract such fractions.
Example 1. Find the meaning of the expression:
These fractions have different denominators, so you need to reduce them to the same (common) denominator.
First we find the LCM of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 4. The least common multiple of these numbers is 12
LCM (3 and 4) = 12
Now let's return to fractions and
Let's find an additional factor for the first fraction. To do this, divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 3. Divide 12 by 3, we get 4. Write a four above the first fraction:
We do the same with the second fraction. Divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 4. Divide 12 by 4, we get 3. Write a three over the second fraction:
Now we are ready for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to subtract such fractions. Let's take this example to the end:

We received an answer
Let's try to depict our solution using a drawing. If you cut pizza from a pizza, you get pizza

This is the detailed version of the solution. If we were at school, we would have to solve this example shorter. Such a solution would look like this:

Reducing fractions to a common denominator can also be depicted using a picture. Reducing these fractions to a common denominator, we got the fractions and . These fractions will be represented by the same pizza slices, but this time they will be divided into equal shares (reduced to the same denominator):

The first picture shows a fraction (eight pieces out of twelve), and the second picture shows a fraction (three pieces out of twelve). By cutting three pieces from eight pieces, we get five pieces out of twelve. The fraction describes these five pieces.
Example 2. Find the value of an expression 
These fractions have different denominators, so first you need to reduce them to the same (common) denominator.
Let's find the LCM of the denominators of these fractions.
The denominators of the fractions are the numbers 10, 3 and 5. The least common multiple of these numbers is 30
LCM(10, 3, 5) = 30
Now we find additional factors for each fraction. To do this, divide the LCM by the denominator of each fraction.
Let's find an additional factor for the first fraction. LCM is the number 30, and the denominator of the first fraction is the number 10. Divide 30 by 10, we get the first additional factor 3. We write it above the first fraction:
Now we find an additional factor for the second fraction. Divide the LCM by the denominator of the second fraction. LCM is the number 30, and the denominator of the second fraction is the number 3. Divide 30 by 3, we get the second additional factor 10. We write it above the second fraction:
Now we find an additional factor for the third fraction. Divide the LCM by the denominator of the third fraction. LCM is the number 30, and the denominator of the third fraction is the number 5. Divide 30 by 5, we get the third additional factor 6. We write it above the third fraction:
Now everything is ready for subtraction. It remains to multiply the fractions by their additional factors:
We came to the conclusion that fractions that had different denominators turned into fractions that had the same (common) denominators. And we already know how to subtract such fractions. Let's finish this example.
The continuation of the example will not fit on one line, so we move the continuation to the next line. Don't forget about the equal sign (=) on the new line:

The answer turned out to be a regular fraction, and everything seems to suit us, but it is too cumbersome and ugly. We should make it simpler. What can be done? You can shorten this fraction.
To reduce a fraction, you need to divide its numerator and denominator by (GCD) of the numbers 20 and 30.
So, we find the gcd of numbers 20 and 30:

Now we return to our example and divide the numerator and denominator of the fraction by the found gcd, that is, by 10

We received an answer
Multiplying a fraction by a number
To multiply a fraction by a number, you need to multiply the numerator of the given fraction by that number and leave the denominator the same.
Example 1. Multiply a fraction by the number 1.
Multiply the numerator of the fraction by the number 1
![]()
The recording can be understood as taking half 1 time. For example, if you take pizza once, you get pizza

From the laws of multiplication we know that if the multiplicand and the factor are swapped, the product will not change. If the expression is written as , then the product will still be equal to . Again, the rule for multiplying a whole number and a fraction works:
![]()
This notation can be understood as taking half of one. For example, if there is 1 whole pizza and we take half of it, then we will have pizza:

Example 2. Find the value of an expression
Multiply the numerator of the fraction by 4
![]()
The answer was an improper fraction. Let's highlight the whole part of it:
![]()
The expression can be understood as taking two quarters 4 times. For example, if you take 4 pizzas, you will get two whole pizzas

And if we swap the multiplicand and the multiplier, we get the expression . It will also be equal to 2. This expression can be understood as taking two pizzas from four whole pizzas:

Multiplying fractions
To multiply fractions, you need to multiply their numerators and denominators. If the answer turns out to be an improper fraction, you need to highlight the whole part of it.
Example 1. Find the value of the expression.
![]()
We received an answer. It is advisable to reduce this fraction. The fraction can be reduced by 2. Then the final solution will take the following form:

The expression can be understood as taking a pizza from half a pizza. Let's say we have half a pizza:
How to take two thirds from this half? First you need to divide this half into three equal parts:

And take two from these three pieces:

We'll make pizza. Remember what pizza looks like when divided into three parts:

One piece of this pizza and the two pieces we took will have the same dimensions:

In other words, we are talking about the same size pizza. Therefore the value of the expression is

Example 2. Find the value of an expression
Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer was an improper fraction. Let's highlight the whole part of it:
![]()
Example 3. Find the value of an expression
Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:
![]()
The answer turned out to be a regular fraction, but it would be good if it was shortened. To reduce this fraction, you need to divide the numerator and denominator of this fraction by the greatest common divisor (GCD) of the numbers 105 and 450.
So, let’s find the gcd of numbers 105 and 450:
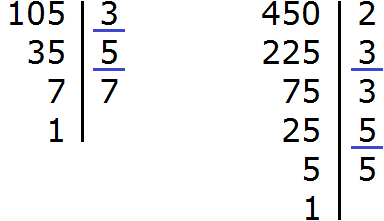
Now we divide the numerator and denominator of our answer by the gcd that we have now found, that is, by 15
Representing a whole number as a fraction
Any whole number can be represented as a fraction. For example, the number 5 can be represented as . This will not change the meaning of five, since the expression means “the number five divided by one,” and this, as we know, is equal to five:
Reciprocal numbers
Now we will get acquainted with a very interesting topic in mathematics. It's called "reverse numbers".
Definition. Reverse to numbera is a number that, when multiplied bya gives one.
Let's substitute in this definition instead of the variable a number 5 and try to read the definition:
Reverse to number 5 is a number that, when multiplied by 5 gives one.
Is it possible to find a number that, when multiplied by 5, gives one? It turns out it is possible. Let's imagine five as a fraction:
Then multiply this fraction by itself, just swap the numerator and denominator. In other words, let’s multiply the fraction by itself, only upside down:
What will happen as a result of this? If we continue to solve this example, we get one:
![]()
This means that the inverse of the number 5 is the number , since when you multiply 5 by you get one.
The reciprocal of a number can also be found for any other integer.
You can also find the reciprocal of any other fraction. To do this, just turn it over.
Dividing a fraction by a number
Let's say we have half a pizza:
Let's divide it equally between two. How much pizza will each person get?

It can be seen that after dividing half the pizza, two equal pieces were obtained, each of which constitutes a pizza. So everyone gets a pizza.
Division of fractions is done using reciprocals. Reciprocal numbers allow you to replace division with multiplication.
To divide a fraction by a number, you need to multiply the fraction by the inverse of the divisor.
Using this rule, we will write down the division of our half of the pizza into two parts.
So, you need to divide the fraction by the number 2. Here the dividend is the fraction and the divisor is the number 2.
To divide a fraction by the number 2, you need to multiply this fraction by the reciprocal of the divisor 2. The reciprocal of the divisor 2 is the fraction. So you need to multiply by
