ಆಪರೇಟರ್‌ನ ಸಮಾನ ಮೌಲ್ಯಗಳನ್ನು ಹುಡುಕಿ. ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು (ಸಂಖ್ಯೆಗಳು) ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು ಪರಿಹಾರಗಳ ಉದಾಹರಣೆಗಳು

ಕರ್ಣೀಯ ಮಾತೃಕೆಗಳು ಸರಳವಾದ ರಚನೆಯನ್ನು ಹೊಂದಿವೆ. ರೇಖೀಯ ಆಪರೇಟರ್‌ನ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಕರ್ಣೀಯ ರೂಪವನ್ನು ಹೊಂದಿರುವ ಆಧಾರವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಸಾಧ್ಯವೇ ಎಂಬ ಪ್ರಶ್ನೆ ಉದ್ಭವಿಸುತ್ತದೆ. ಅಂತಹ ಆಧಾರವು ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ.
ನಮಗೆ ರೇಖೀಯ ಜಾಗವನ್ನು ನೀಡೋಣ R n ಮತ್ತು ರೇಖೀಯ ಆಪರೇಟರ್ A ಅದರಲ್ಲಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ; ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಆಪರೇಟರ್ A R n ಅನ್ನು ತನ್ನೊಳಗೆ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ, ಅಂದರೆ A:R n → R n .

ವ್ಯಾಖ್ಯಾನ. ಶೂನ್ಯವಲ್ಲದ ವೆಕ್ಟರ್ ಅನ್ನು ಆಪರೇಟರ್ A ಯ ಐಜೆನ್ವೆಕ್ಟರ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಆಪರೇಟರ್ A ಅನ್ನು ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್ ಆಗಿ ಭಾಷಾಂತರಿಸಿದರೆ, ಅಂದರೆ. λ ಸಂಖ್ಯೆಯನ್ನು ಐಜೆನ್‌ವೆಕ್ಟರ್‌ಗೆ ಅನುಗುಣವಾಗಿ ಆಪರೇಟರ್ A ನ ಐಜೆನ್‌ವಾಲ್ಯೂ ಅಥವಾ ಐಜೆನ್‌ವಾಲ್ಯೂ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಐಜೆನ್ವಾಲ್ಯೂಸ್ ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್ಗಳ ಕೆಲವು ಗುಣಲಕ್ಷಣಗಳನ್ನು ನಾವು ಗಮನಿಸೋಣ.
1. ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ಯಾವುದೇ ರೇಖೀಯ ಸಂಯೋಜನೆ ಅದೇ ಐಜೆನ್‌ವಾಲ್ಯೂಗೆ ಅನುಗುಣವಾದ ಆಪರೇಟರ್ ಎ λ ಅದೇ ಐಜೆನ್‌ವಾಲ್ಯೂ ಹೊಂದಿರುವ ಐಜೆನ್‌ವೆಕ್ಟರ್ ಆಗಿದೆ.
2. ಐಜೆನ್ವೆಕ್ಟರ್ಸ್ λ 1, λ 2, ..., λ m ಜೋಡಿಯಾಗಿ ವಿಭಿನ್ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳೊಂದಿಗೆ ಆಪರೇಟರ್ A ರೇಖಾತ್ಮಕವಾಗಿ ಸ್ವತಂತ್ರವಾಗಿದೆ.
3. ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು λ 1 = λ 2 = λ m = λ ಆಗಿದ್ದರೆ, ಐಜೆನ್‌ವಾಲ್ಯೂ λ m ರೇಖಾತ್ಮಕವಾಗಿ ಸ್ವತಂತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳಿಗಿಂತ ಹೆಚ್ಚಿಲ್ಲ.

ಆದ್ದರಿಂದ, n ರೇಖಾತ್ಮಕವಾಗಿ ಸ್ವತಂತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳಿದ್ದರೆ , ವಿಭಿನ್ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳಿಗೆ ಅನುಗುಣವಾಗಿ λ 1, λ 2, ..., λ n, ನಂತರ ಅವು ರೇಖಾತ್ಮಕವಾಗಿ ಸ್ವತಂತ್ರವಾಗಿರುತ್ತವೆ, ಆದ್ದರಿಂದ, ಅವುಗಳನ್ನು R n ಸ್ಥಳದ ಆಧಾರವಾಗಿ ತೆಗೆದುಕೊಳ್ಳಬಹುದು. ರೇಖೀಯ ಆಪರೇಟರ್ A ನ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ರೂಪವನ್ನು ಅದರ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ಆಧಾರದ ಮೇಲೆ ಕಂಡುಹಿಡಿಯೋಣ, ಇದಕ್ಕಾಗಿ ನಾವು ನಿರ್ವಾಹಕರು A ನೊಂದಿಗೆ ವೆಕ್ಟರ್ ಆಧಾರದ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತೇವೆ: ನಂತರ .
ಹೀಗಾಗಿ, ಅದರ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳ ಆಧಾರದ ಮೇಲೆ ರೇಖೀಯ ಆಪರೇಟರ್ A ಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಕರ್ಣೀಯ ರೂಪವನ್ನು ಹೊಂದಿದೆ ಮತ್ತು ಆಪರೇಟರ್ A ಯ ಐಜೆನ್ವ್ಯಾಲ್ಯೂಗಳು ಕರ್ಣೀಯ ಉದ್ದಕ್ಕೂ ಇರುತ್ತವೆ.
ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಕರ್ಣೀಯ ರೂಪವನ್ನು ಹೊಂದಿರುವ ಇನ್ನೊಂದು ಆಧಾರವಿದೆಯೇ? ಈ ಪ್ರಶ್ನೆಗೆ ಉತ್ತರವನ್ನು ಈ ಕೆಳಗಿನ ಪ್ರಮೇಯದಿಂದ ನೀಡಲಾಗಿದೆ.

ಪ್ರಮೇಯ. ಆಧಾರದಲ್ಲಿ (i = 1..n) ಲೀನಿಯರ್ ಆಪರೇಟರ್ A ಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಒಂದು ಕರ್ಣೀಯ ರೂಪವನ್ನು ಹೊಂದಿರುತ್ತದೆ ಮತ್ತು ಆಧಾರದ ಎಲ್ಲಾ ವೆಕ್ಟರ್‌ಗಳು ಆಪರೇಟರ್ A ನ ಐಜೆನ್ವೆಕ್ಟರ್ ಆಗಿದ್ದರೆ ಮಾತ್ರ.

ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವ ನಿಯಮ

. (*)

(1)
ಎಲ್ಲಿ - ಲೀನಿಯರ್ ಆಪರೇಟರ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್.

ಸಿಸ್ಟಮ್ (1) ಅದರ ಡಿಟರ್ಮಿನಂಟ್ D ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿದ್ದರೆ ಶೂನ್ಯವಲ್ಲದ ಪರಿಹಾರವನ್ನು ಹೊಂದಿರುತ್ತದೆ

ಉದಾಹರಣೆ 12. ಲೀನಿಯರ್ ಆಪರೇಟರ್ A ಕಾನೂನಿನ ಪ್ರಕಾರ R 3 ನಲ್ಲಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ, ಅಲ್ಲಿ x 1, x 2, .., x n ಆಧಾರದಲ್ಲಿ ವೆಕ್ಟರ್‌ನ ನಿರ್ದೇಶಾಂಕಗಳಾಗಿವೆ. , , . ಈ ಆಪರೇಟರ್‌ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಹುಡುಕಿ.
ಪರಿಹಾರ. ನಾವು ಈ ಆಪರೇಟರ್‌ನ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ನಿರ್ಮಿಸುತ್ತೇವೆ:
.
ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ನಿರ್ಧರಿಸಲು ನಾವು ವ್ಯವಸ್ಥೆಯನ್ನು ರಚಿಸುತ್ತೇವೆ:

ನಾವು ವಿಶಿಷ್ಟ ಸಮೀಕರಣವನ್ನು ರಚಿಸುತ್ತೇವೆ ಮತ್ತು ಅದನ್ನು ಪರಿಹರಿಸುತ್ತೇವೆ:

.
λ 1,2 = -1, λ 3 = 3.
ಸಿಸ್ಟಂನಲ್ಲಿ λ = -1 ಅನ್ನು ಬದಲಿಸುವುದು, ನಾವು ಹೊಂದಿದ್ದೇವೆ:
ಅಥವಾ
ಏಕೆಂದರೆ , ನಂತರ ಎರಡು ಅವಲಂಬಿತ ಅಸ್ಥಿರಗಳು ಮತ್ತು ಒಂದು ಉಚಿತ ವೇರಿಯೇಬಲ್ ಇವೆ.
x 1 ಉಚಿತ ಅಜ್ಞಾತವಾಗಿರಲಿ ನಾವು ಈ ವ್ಯವಸ್ಥೆಯನ್ನು ಯಾವುದೇ ರೀತಿಯಲ್ಲಿ ಪರಿಹರಿಸುತ್ತೇವೆ ಮತ್ತು ಈ ವ್ಯವಸ್ಥೆಯ ಸಾಮಾನ್ಯ ಪರಿಹಾರವನ್ನು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ: ಪರಿಹಾರಗಳ ಮೂಲಭೂತ ವ್ಯವಸ್ಥೆಯು ಒಂದು ಪರಿಹಾರವನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ, ಏಕೆಂದರೆ n - r = 3 - 2 = 1.
λ = -1 ಐಜೆನ್‌ವಾಲ್ಯೂಗೆ ಅನುಗುಣವಾದ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ಸೆಟ್ ರೂಪವನ್ನು ಹೊಂದಿದೆ: , ಇಲ್ಲಿ x 1 ಶೂನ್ಯವನ್ನು ಹೊರತುಪಡಿಸಿ ಯಾವುದೇ ಸಂಖ್ಯೆಯಾಗಿದೆ. ಈ ಸೆಟ್‌ನಿಂದ ಒಂದು ವೆಕ್ಟರ್ ಅನ್ನು ಆಯ್ಕೆ ಮಾಡೋಣ, ಉದಾಹರಣೆಗೆ, x 1 = 1 ಅನ್ನು ಹಾಕುವುದು: .
ಇದೇ ರೀತಿ ತಾರ್ಕಿಕವಾಗಿ, ಐಜೆನ್‌ವೆಕ್ಟರ್ ಅನ್ನು ಐಜೆನ್‌ವಾಲ್ಯೂ λ = 3 ಗೆ ಅನುಗುಣವಾದುದನ್ನು ನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ: .
ಬಾಹ್ಯಾಕಾಶ R 3 ನಲ್ಲಿ, ಆಧಾರವು ಮೂರು ರೇಖೀಯ ಸ್ವತಂತ್ರ ವೆಕ್ಟರ್‌ಗಳನ್ನು ಒಳಗೊಂಡಿದೆ, ಆದರೆ ನಾವು ಕೇವಲ ಎರಡು ರೇಖೀಯ ಸ್ವತಂತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಮಾತ್ರ ಸ್ವೀಕರಿಸಿದ್ದೇವೆ, ಇದರಿಂದ R 3 ನಲ್ಲಿ ಆಧಾರವನ್ನು ಸಂಯೋಜಿಸಲಾಗುವುದಿಲ್ಲ. ಪರಿಣಾಮವಾಗಿ, ನಾವು ರೇಖೀಯ ಆಪರೇಟರ್‌ನ ಮ್ಯಾಟ್ರಿಕ್ಸ್ A ಅನ್ನು ಕರ್ಣೀಯ ರೂಪಕ್ಕೆ ಕಡಿಮೆ ಮಾಡಲು ಸಾಧ್ಯವಿಲ್ಲ.

ಉದಾಹರಣೆ 13. ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನೀಡಲಾಗಿದೆ .
1. ವೆಕ್ಟರ್ ಎಂದು ಸಾಬೀತುಪಡಿಸಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್ A ಯ ಐಜೆನ್ವೆಕ್ಟರ್ ಆಗಿದೆ. ಈ ಐಜೆನ್ವೆಕ್ಟರ್ಗೆ ಅನುಗುಣವಾದ ಐಜೆನ್ವಾಲ್ಯೂ ಅನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
2. ಮ್ಯಾಟ್ರಿಕ್ಸ್ A ಕರ್ಣೀಯ ರೂಪವನ್ನು ಹೊಂದಿರುವ ಆಧಾರವನ್ನು ಹುಡುಕಿ.
ಪರಿಹಾರ.
1. ಆಗಿದ್ದರೆ, ಅದು ಐಜೆನ್ವೆಕ್ಟರ್ ಆಗಿದೆ

.
ವೆಕ್ಟರ್ (1, 8, -1) ಒಂದು ಐಜೆನ್ವೆಕ್ಟರ್ ಆಗಿದೆ. ಐಜೆನ್‌ವಾಲ್ಯೂ λ = -1.
ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಆಧಾರದಲ್ಲಿ ಕರ್ಣೀಯ ರೂಪವನ್ನು ಹೊಂದಿದೆ. ಅವುಗಳಲ್ಲಿ ಒಂದು ಪ್ರಸಿದ್ಧವಾಗಿದೆ. ಉಳಿದದ್ದನ್ನು ಕಂಡುಹಿಡಿಯೋಣ.
ನಾವು ವ್ಯವಸ್ಥೆಯಿಂದ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಹುಡುಕುತ್ತೇವೆ:

ವಿಶಿಷ್ಟ ಸಮೀಕರಣ: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
λ = -3 ಈಜೆನ್‌ವಾಲ್ಯೂಗೆ ಅನುಗುಣವಾದ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

ಈ ವ್ಯವಸ್ಥೆಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಶ್ರೇಣಿಯು ಎರಡು ಮತ್ತು ಅಪರಿಚಿತರ ಸಂಖ್ಯೆಗೆ ಸಮನಾಗಿರುತ್ತದೆ, ಆದ್ದರಿಂದ ಈ ವ್ಯವಸ್ಥೆಯು ಶೂನ್ಯ ಪರಿಹಾರವನ್ನು ಮಾತ್ರ ಹೊಂದಿದೆ x 1 = x 3 = 0. ಇಲ್ಲಿ x 2 ಶೂನ್ಯವನ್ನು ಹೊರತುಪಡಿಸಿ ಬೇರೆ ಯಾವುದಾದರೂ ಆಗಿರಬಹುದು, ಉದಾಹರಣೆಗೆ, x 2 = 1. ಹೀಗಾಗಿ, ವೆಕ್ಟರ್ (0 ,1,0) λ = -3 ಗೆ ಅನುಗುಣವಾದ ಐಜೆನ್ವೆಕ್ಟರ್ ಆಗಿದೆ. ಪರಿಶೀಲಿಸೋಣ:
.
λ = 1 ಆಗಿದ್ದರೆ, ನಾವು ಸಿಸ್ಟಮ್ ಅನ್ನು ಪಡೆಯುತ್ತೇವೆ
ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಶ್ರೇಣಿ ಎರಡು. ನಾವು ಕೊನೆಯ ಸಮೀಕರಣವನ್ನು ದಾಟುತ್ತೇವೆ.
x 3 ಉಚಿತ ಅಜ್ಞಾತವಾಗಿರಲಿ. ನಂತರ x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
x 3 = 1 ಎಂದು ಭಾವಿಸಿದರೆ, ನಾವು (-3,-9,1) ಹೊಂದಿದ್ದೇವೆ - ಈಜೆನ್‌ವಾಲ್ಯೂ λ = 1 ಗೆ ಅನುಗುಣವಾದ ಐಜೆನ್ವೆಕ್ಟರ್. ಪರಿಶೀಲಿಸಿ:

.
ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ನೈಜ ಮತ್ತು ವಿಭಿನ್ನವಾಗಿರುವುದರಿಂದ, ಅವುಗಳಿಗೆ ಅನುಗುಣವಾದ ವಾಹಕಗಳು ರೇಖಾತ್ಮಕವಾಗಿ ಸ್ವತಂತ್ರವಾಗಿರುತ್ತವೆ, ಆದ್ದರಿಂದ ಅವುಗಳನ್ನು R 3 ನಲ್ಲಿ ಆಧಾರವಾಗಿ ತೆಗೆದುಕೊಳ್ಳಬಹುದು. ಹೀಗಾಗಿ, ಆಧಾರದ ಮೇಲೆ , , ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ ರೂಪವನ್ನು ಹೊಂದಿದೆ:
.
ರೇಖೀಯ ಆಪರೇಟರ್ A:R n → R n ನ ಪ್ರತಿಯೊಂದು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಕರ್ಣೀಯ ರೂಪಕ್ಕೆ ಇಳಿಸಲಾಗುವುದಿಲ್ಲ, ಏಕೆಂದರೆ ಕೆಲವು ರೇಖೀಯ ಆಪರೇಟರ್‌ಗಳಿಗೆ n ರೇಖೀಯ ಸ್ವತಂತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳಿಗಿಂತ ಕಡಿಮೆ ಇರಬಹುದು. ಆದಾಗ್ಯೂ, ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಸಮ್ಮಿತೀಯವಾಗಿದ್ದರೆ, ಗುಣಾಕಾರ m ನ ವಿಶಿಷ್ಟ ಸಮೀಕರಣದ ಮೂಲವು ನಿಖರವಾಗಿ m ರೇಖೀಯ ಸ್ವತಂತ್ರ ವೆಕ್ಟರ್‌ಗಳಿಗೆ ಅನುರೂಪವಾಗಿದೆ.

ವ್ಯಾಖ್ಯಾನ. ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಒಂದು ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ, ಇದರಲ್ಲಿ ಮುಖ್ಯ ಕರ್ಣೀಯ ಸಮ್ಮಿತೀಯ ಅಂಶಗಳು ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ, ಇದರಲ್ಲಿ .
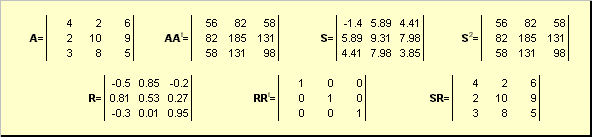
ಟಿಪ್ಪಣಿಗಳು. 1. ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಎಲ್ಲಾ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ನೈಜವಾಗಿವೆ.
2. ಜೋಡಿಯಾಗಿ ವಿಭಿನ್ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳಿಗೆ ಅನುಗುಣವಾದ ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು ಆರ್ಥೋಗೋನಲ್ ಆಗಿರುತ್ತವೆ.
ಅಧ್ಯಯನ ಮಾಡಿದ ಉಪಕರಣದ ಅನೇಕ ಅಪ್ಲಿಕೇಶನ್‌ಗಳಲ್ಲಿ ಒಂದಾಗಿ, ಎರಡನೇ ಕ್ರಮಾಂಕದ ಕರ್ವ್‌ನ ಪ್ರಕಾರವನ್ನು ನಿರ್ಧರಿಸುವ ಸಮಸ್ಯೆಯನ್ನು ನಾವು ಪರಿಗಣಿಸುತ್ತೇವೆ.

ಐಜೆನ್‌ವಾಲ್ಯೂಸ್ (ಸಂಖ್ಯೆಗಳು) ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು.
ಪರಿಹಾರಗಳ ಉದಾಹರಣೆಗಳು

ನೀನು ನೀನಾಗಿರು

ಎರಡೂ ಸಮೀಕರಣಗಳಿಂದ ಅದು ಅನುಸರಿಸುತ್ತದೆ.

ನಂತರ ಅದನ್ನು ಹಾಕೋಣ: .

ಪರಿಣಾಮವಾಗಿ: - ಎರಡನೇ ಐಜೆನ್ವೆಕ್ಟರ್.

ನಿರ್ಧಾರದ ಪ್ರಮುಖ ಅಂಶಗಳನ್ನು ನಾವು ಪುನರಾವರ್ತಿಸೋಣ:

- ಪರಿಣಾಮವಾಗಿ ವ್ಯವಸ್ಥೆಯು ಖಂಡಿತವಾಗಿಯೂ ಸಾಮಾನ್ಯ ಪರಿಹಾರವನ್ನು ಹೊಂದಿದೆ (ಸಮೀಕರಣಗಳು ರೇಖಾತ್ಮಕವಾಗಿ ಅವಲಂಬಿತವಾಗಿವೆ);

- ನಾವು "y" ಅನ್ನು ಪೂರ್ಣಾಂಕದ ರೀತಿಯಲ್ಲಿ ಆಯ್ಕೆ ಮಾಡುತ್ತೇವೆ ಮತ್ತು ಮೊದಲ "x" ನಿರ್ದೇಶಾಂಕವು ಪೂರ್ಣಾಂಕ, ಧನಾತ್ಮಕ ಮತ್ತು ಸಾಧ್ಯವಾದಷ್ಟು ಚಿಕ್ಕದಾಗಿದೆ.

- ನಿರ್ದಿಷ್ಟ ಪರಿಹಾರವು ವ್ಯವಸ್ಥೆಯ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆಯೇ ಎಂದು ನಾವು ಪರಿಶೀಲಿಸುತ್ತೇವೆ.

ಉತ್ತರ .

ಸಾಕಷ್ಟು ಮಧ್ಯಂತರ "ಚೆಕ್‌ಪಾಯಿಂಟ್‌ಗಳು" ಇದ್ದವು, ಆದ್ದರಿಂದ ಸಮಾನತೆಯನ್ನು ಪರಿಶೀಲಿಸುವುದು ತಾತ್ವಿಕವಾಗಿ ಅನಗತ್ಯವಾಗಿದೆ.

ಮಾಹಿತಿಯ ವಿವಿಧ ಮೂಲಗಳಲ್ಲಿ, ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಕಾಲಮ್‌ಗಳಲ್ಲಿ ಬರೆಯಲಾಗುವುದಿಲ್ಲ, ಆದರೆ ಸಾಲುಗಳಲ್ಲಿ ಬರೆಯಲಾಗುತ್ತದೆ, ಉದಾಹರಣೆಗೆ: (ಮತ್ತು, ಪ್ರಾಮಾಣಿಕವಾಗಿ ಹೇಳಬೇಕೆಂದರೆ, ನಾನು ಅವುಗಳನ್ನು ಸಾಲುಗಳಲ್ಲಿ ಬರೆಯಲು ಬಳಸಲಾಗುತ್ತದೆ). ಈ ಆಯ್ಕೆಯು ಸ್ವೀಕಾರಾರ್ಹವಾಗಿದೆ, ಆದರೆ ವಿಷಯದ ಬೆಳಕಿನಲ್ಲಿ ರೇಖೀಯ ರೂಪಾಂತರಗಳುತಾಂತ್ರಿಕವಾಗಿ ಬಳಸಲು ಹೆಚ್ಚು ಅನುಕೂಲಕರವಾಗಿದೆ ಕಾಲಮ್ ವಾಹಕಗಳು.

ಬಹುಶಃ ಪರಿಹಾರವು ನಿಮಗೆ ಬಹಳ ಉದ್ದವಾಗಿದೆ ಎಂದು ತೋರುತ್ತದೆ, ಆದರೆ ಇದು ನಾನು ಮೊದಲ ಉದಾಹರಣೆಯನ್ನು ಹೆಚ್ಚು ವಿವರವಾಗಿ ಕಾಮೆಂಟ್ ಮಾಡಿದ್ದರಿಂದ ಮಾತ್ರ.

ಉದಾಹರಣೆ 2

ಮ್ಯಾಟ್ರಿಸಸ್

ಸ್ವಂತವಾಗಿ ತರಬೇತಿ ನೀಡೋಣ! ಪಾಠದ ಕೊನೆಯಲ್ಲಿ ಅಂತಿಮ ಕಾರ್ಯದ ಅಂದಾಜು ಉದಾಹರಣೆ.

ಕೆಲವೊಮ್ಮೆ ನೀವು ಹೆಚ್ಚುವರಿ ಕಾರ್ಯವನ್ನು ಪೂರ್ಣಗೊಳಿಸಬೇಕಾಗುತ್ತದೆ, ಅವುಗಳೆಂದರೆ:

ಅಂಗೀಕೃತ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವಿಭಜನೆಯನ್ನು ಬರೆಯಿರಿ

ಅದು ಏನು?

ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು ರೂಪುಗೊಂಡರೆ ಆಧಾರದ, ನಂತರ ಇದನ್ನು ಹೀಗೆ ಪ್ರತಿನಿಧಿಸಬಹುದು:

ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ಕೂಡಿದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಲ್ಲಿದೆ, - ಕರ್ಣೀಯಅನುಗುಣವಾದ ಐಜೆನ್ವಾಲ್ಯೂಗಳೊಂದಿಗೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್.

ಈ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವಿಭಜನೆಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಅಂಗೀಕೃತಅಥವಾ ಕರ್ಣೀಯ.

ಮೊದಲ ಉದಾಹರಣೆಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ನೋಡೋಣ. ಇದರ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು ರೇಖೀಯವಾಗಿ ಸ್ವತಂತ್ರ(ಕಾಲಿನಿಯರ್ ಅಲ್ಲದ) ಮತ್ತು ಆಧಾರವನ್ನು ರೂಪಿಸುತ್ತದೆ. ಅವರ ನಿರ್ದೇಶಾಂಕಗಳ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ರಚಿಸೋಣ:

ಆನ್ ಮುಖ್ಯ ಕರ್ಣೀಯಮ್ಯಾಟ್ರಿಕ್ಸ್ ಸೂಕ್ತ ಕ್ರಮದಲ್ಲಿಐಜೆನ್ವಾಲ್ಯೂಗಳು ನೆಲೆಗೊಂಡಿವೆ, ಮತ್ತು ಉಳಿದ ಅಂಶಗಳು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:
- ನಾನು ಮತ್ತೊಮ್ಮೆ ಆದೇಶದ ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು ಒತ್ತಿಹೇಳುತ್ತೇನೆ: "ಎರಡು" 1 ನೇ ವೆಕ್ಟರ್ಗೆ ಅನುರೂಪವಾಗಿದೆ ಮತ್ತು ಆದ್ದರಿಂದ 1 ನೇ ಕಾಲಮ್ನಲ್ಲಿ "ಮೂರು" - 2 ನೇ ವೆಕ್ಟರ್ಗೆ ಇದೆ.

ಹುಡುಕಲು ಸಾಮಾನ್ಯ ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಬಳಸುವುದು ವಿಲೋಮ ಮ್ಯಾಟ್ರಿಕ್ಸ್ಅಥವಾ ಗಾಸ್-ಜೋರ್ಡಾನ್ ವಿಧಾನನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ . ಇಲ್ಲ, ಅದು ಮುದ್ರಣದೋಷವಲ್ಲ! - ನಿಮ್ಮ ಮೊದಲು ಒಂದು ಅಪರೂಪದ ಘಟನೆಯಾಗಿದೆ, ಸೂರ್ಯಗ್ರಹಣದಂತೆ, ರಿವರ್ಸ್ ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾದಾಗ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಅಂಗೀಕೃತ ವಿಭಜನೆಯನ್ನು ಬರೆಯಲು ಇದು ಉಳಿದಿದೆ:

ಪ್ರಾಥಮಿಕ ರೂಪಾಂತರಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಸಿಸ್ಟಮ್ ಅನ್ನು ಪರಿಹರಿಸಬಹುದು, ಮತ್ತು ಕೆಳಗಿನ ಉದಾಹರಣೆಗಳಲ್ಲಿ ನಾವು ಈ ವಿಧಾನವನ್ನು ಆಶ್ರಯಿಸುತ್ತೇವೆ. ಆದರೆ ಇಲ್ಲಿ "ಶಾಲೆ" ವಿಧಾನವು ಹೆಚ್ಚು ವೇಗವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ. 3 ನೇ ಸಮೀಕರಣದಿಂದ ನಾವು ವ್ಯಕ್ತಪಡಿಸುತ್ತೇವೆ: - ಎರಡನೇ ಸಮೀಕರಣಕ್ಕೆ ಬದಲಿಯಾಗಿ:

ಮೊದಲ ನಿರ್ದೇಶಾಂಕವು ಶೂನ್ಯವಾಗಿರುವುದರಿಂದ, ನಾವು ಒಂದು ವ್ಯವಸ್ಥೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ, ಅದರ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣದಿಂದ ಅದು ಅನುಸರಿಸುತ್ತದೆ .

ಮತ್ತು ಮತ್ತೆ ರೇಖೀಯ ಸಂಬಂಧದ ಕಡ್ಡಾಯ ಉಪಸ್ಥಿತಿಗೆ ಗಮನ ಕೊಡಿ. ಕ್ಷುಲ್ಲಕ ಪರಿಹಾರ ಮಾತ್ರ ಸಿಕ್ಕಿದರೆ , ನಂತರ ಐಜೆನ್‌ವಾಲ್ಯೂ ತಪ್ಪಾಗಿ ಕಂಡುಬಂದಿದೆ, ಅಥವಾ ಸಿಸ್ಟಮ್ ಅನ್ನು ಕಂಪೈಲ್ ಮಾಡಲಾಗಿದೆ/ದೋಷದೊಂದಿಗೆ ಪರಿಹರಿಸಲಾಗಿದೆ.

ಕಾಂಪ್ಯಾಕ್ಟ್ ನಿರ್ದೇಶಾಂಕಗಳು ಮೌಲ್ಯವನ್ನು ನೀಡುತ್ತದೆ

ಐಜೆನ್ವೆಕ್ಟರ್:

ಮತ್ತು ಮತ್ತೊಮ್ಮೆ, ನಾವು ಪರಿಹಾರವನ್ನು ಕಂಡುಕೊಂಡಿದ್ದೇವೆ ಎಂದು ಪರಿಶೀಲಿಸುತ್ತೇವೆ ವ್ಯವಸ್ಥೆಯ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆ. ನಂತರದ ಪ್ಯಾರಾಗಳಲ್ಲಿ ಮತ್ತು ನಂತರದ ಕಾರ್ಯಗಳಲ್ಲಿ, ಈ ಆಶಯವನ್ನು ಕಡ್ಡಾಯ ನಿಯಮವಾಗಿ ತೆಗೆದುಕೊಳ್ಳಲು ನಾನು ಶಿಫಾರಸು ಮಾಡುತ್ತೇವೆ.

2) ಐಜೆನ್‌ವಾಲ್ಯೂಗಾಗಿ, ಅದೇ ತತ್ವವನ್ನು ಬಳಸಿಕೊಂಡು, ನಾವು ಈ ಕೆಳಗಿನ ವ್ಯವಸ್ಥೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ:

ಸಿಸ್ಟಮ್ನ 2 ನೇ ಸಮೀಕರಣದಿಂದ ನಾವು ವ್ಯಕ್ತಪಡಿಸುತ್ತೇವೆ: - ಮೂರನೇ ಸಮೀಕರಣಕ್ಕೆ ಬದಲಿಯಾಗಿ:

"ಝೀಟಾ" ನಿರ್ದೇಶಾಂಕವು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುವುದರಿಂದ, ರೇಖೀಯ ಅವಲಂಬನೆಯನ್ನು ಅನುಸರಿಸುವ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣದಿಂದ ನಾವು ವ್ಯವಸ್ಥೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ.

ಅವಕಾಶ

ಪರಿಹಾರವನ್ನು ಪರಿಶೀಲಿಸಲಾಗುತ್ತಿದೆ ವ್ಯವಸ್ಥೆಯ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆ.

ಹೀಗಾಗಿ, ಐಜೆನ್ವೆಕ್ಟರ್: .

3) ಮತ್ತು ಅಂತಿಮವಾಗಿ, ಸಿಸ್ಟಮ್ ಐಜೆನ್ವಾಲ್ಯೂಗೆ ಅನುರೂಪವಾಗಿದೆ:

ಎರಡನೆಯ ಸಮೀಕರಣವು ಸರಳವಾಗಿ ಕಾಣುತ್ತದೆ, ಆದ್ದರಿಂದ ನಾವು ಅದನ್ನು ವ್ಯಕ್ತಪಡಿಸೋಣ ಮತ್ತು ಅದನ್ನು 1 ನೇ ಮತ್ತು 3 ನೇ ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸೋಣ:

ಎಲ್ಲವೂ ಉತ್ತಮವಾಗಿದೆ - ರೇಖಾತ್ಮಕ ಸಂಬಂಧವು ಹೊರಹೊಮ್ಮಿದೆ, ಅದನ್ನು ನಾವು ಅಭಿವ್ಯಕ್ತಿಗೆ ಬದಲಿಸುತ್ತೇವೆ:

ಪರಿಣಾಮವಾಗಿ, "x" ಮತ್ತು "y" ಅನ್ನು "z" ಮೂಲಕ ವ್ಯಕ್ತಪಡಿಸಲಾಗಿದೆ: . ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಅಂತಹ ಸಂಬಂಧಗಳನ್ನು ನಿಖರವಾಗಿ ಸಾಧಿಸುವುದು ಅನಿವಾರ್ಯವಲ್ಲ; ಕೆಲವು ಸಂದರ್ಭಗಳಲ್ಲಿ ಮೂಲಕ ಅಥವಾ ಮತ್ತು ಮೂಲಕ ವ್ಯಕ್ತಪಡಿಸಲು ಹೆಚ್ಚು ಅನುಕೂಲಕರವಾಗಿದೆ. ಅಥವಾ "ರೈಲು" - ಉದಾಹರಣೆಗೆ, "X" ಮೂಲಕ "I", ಮತ್ತು "I" ಮೂಲಕ "Z"

ನಂತರ ಅದನ್ನು ಹಾಕೋಣ:

ಪರಿಹಾರ ಕಂಡುಬಂದಿದೆಯೇ ಎಂದು ನಾವು ಪರಿಶೀಲಿಸುತ್ತೇವೆ ವ್ಯವಸ್ಥೆಯ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣವನ್ನು ತೃಪ್ತಿಪಡಿಸುತ್ತದೆ ಮತ್ತು ಮೂರನೇ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಬರೆಯುತ್ತದೆ

ಉತ್ತರ: ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು:

ಜ್ಯಾಮಿತೀಯವಾಗಿ, ಈ ವಾಹಕಗಳು ಮೂರು ವಿಭಿನ್ನ ಪ್ರಾದೇಶಿಕ ದಿಕ್ಕುಗಳನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುತ್ತವೆ ("ಅಲ್ಲಿ ಮತ್ತು ಮತ್ತೆ ಮತ್ತೆ"), ಅದರ ಪ್ರಕಾರ ರೇಖೀಯ ರೂಪಾಂತರಶೂನ್ಯವಲ್ಲದ ವೆಕ್ಟರ್‌ಗಳನ್ನು (ಐಜೆನ್‌ವೆಕ್ಟರ್‌ಗಳು) ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್‌ಗಳಾಗಿ ಪರಿವರ್ತಿಸುತ್ತದೆ.

ಸ್ಥಿತಿಯು ಅಂಗೀಕೃತ ವಿಭಜನೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವ ಅಗತ್ಯವಿದ್ದರೆ, ಇದು ಇಲ್ಲಿ ಸಾಧ್ಯ, ಏಕೆಂದರೆ ವಿಭಿನ್ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ವಿಭಿನ್ನ ರೇಖಾತ್ಮಕವಾಗಿ ಸ್ವತಂತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳಿಗೆ ಸಂಬಂಧಿಸಿವೆ. ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಮಾಡುವುದು ಅವುಗಳ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ, ಕರ್ಣೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನಿಂದ ಸಂಬಂಧಿತಸಮಾನ ಮೌಲ್ಯಗಳು ಮತ್ತು ಕಂಡುಹಿಡಿಯಿರಿ ವಿಲೋಮ ಮ್ಯಾಟ್ರಿಕ್ಸ್ .

ಷರತ್ತಿನ ಪ್ರಕಾರ, ನೀವು ಬರೆಯಬೇಕಾದರೆ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ಆಧಾರದ ಮೇಲೆ ರೇಖೀಯ ರೂಪಾಂತರ ಮ್ಯಾಟ್ರಿಕ್ಸ್, ನಂತರ ನಾವು ರೂಪದಲ್ಲಿ ಉತ್ತರವನ್ನು ನೀಡುತ್ತೇವೆ. ವ್ಯತ್ಯಾಸವಿದೆ, ಮತ್ತು ವ್ಯತ್ಯಾಸವು ಗಮನಾರ್ಹವಾಗಿದೆ!ಏಕೆಂದರೆ ಈ ಮ್ಯಾಟ್ರಿಕ್ಸ್ "ಡಿ" ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ.

ನೀವೇ ಪರಿಹರಿಸಲು ಸರಳವಾದ ಲೆಕ್ಕಾಚಾರಗಳೊಂದಿಗಿನ ಸಮಸ್ಯೆ:

ಉದಾಹರಣೆ 5

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನೀಡಿದ ರೇಖೀಯ ರೂಪಾಂತರದ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳನ್ನು ಹುಡುಕಿ

ನಿಮ್ಮ ಸ್ವಂತ ಸಂಖ್ಯೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವಾಗ, 3 ನೇ ಡಿಗ್ರಿ ಬಹುಪದಕ್ಕೆ ಹೋಗದಿರಲು ಪ್ರಯತ್ನಿಸಿ. ಹೆಚ್ಚುವರಿಯಾಗಿ, ನಿಮ್ಮ ಸಿಸ್ಟಮ್ ಪರಿಹಾರಗಳು ನನ್ನ ಪರಿಹಾರಗಳಿಂದ ಭಿನ್ನವಾಗಿರಬಹುದು - ಇಲ್ಲಿ ಯಾವುದೇ ಖಚಿತತೆ ಇಲ್ಲ; ಮತ್ತು ನೀವು ಕಂಡುಕೊಳ್ಳುವ ವೆಕ್ಟರ್‌ಗಳು ಮಾದರಿ ವೆಕ್ಟರ್‌ಗಳಿಂದ ಅವುಗಳ ಸಂಬಂಧಿತ ನಿರ್ದೇಶಾಂಕಗಳ ಅನುಪಾತದವರೆಗೆ ಭಿನ್ನವಾಗಿರಬಹುದು. ಉದಾಹರಣೆಗೆ, ಮತ್ತು. ಉತ್ತರವನ್ನು ರೂಪದಲ್ಲಿ ಪ್ರಸ್ತುತಪಡಿಸಲು ಇದು ಹೆಚ್ಚು ಕಲಾತ್ಮಕವಾಗಿ ಆಹ್ಲಾದಕರವಾಗಿರುತ್ತದೆ, ಆದರೆ ನೀವು ಎರಡನೇ ಆಯ್ಕೆಯಲ್ಲಿ ನಿಲ್ಲಿಸಿದರೆ ಪರವಾಗಿಲ್ಲ. ಆದಾಗ್ಯೂ, ಎಲ್ಲದಕ್ಕೂ ಸಮಂಜಸವಾದ ಮಿತಿಗಳಿವೆ; ಆವೃತ್ತಿಯು ಇನ್ನು ಮುಂದೆ ಉತ್ತಮವಾಗಿ ಕಾಣುವುದಿಲ್ಲ.

ಪಾಠದ ಕೊನೆಯಲ್ಲಿ ನಿಯೋಜನೆಯ ಅಂದಾಜು ಅಂತಿಮ ಮಾದರಿ.

ಬಹು ಐಜೆನ್‌ವಾಲ್ಯೂಗಳ ಸಂದರ್ಭದಲ್ಲಿ ಸಮಸ್ಯೆಯನ್ನು ಹೇಗೆ ಪರಿಹರಿಸುವುದು?

ಸಾಮಾನ್ಯ ಅಲ್ಗಾರಿದಮ್ ಒಂದೇ ಆಗಿರುತ್ತದೆ, ಆದರೆ ಇದು ತನ್ನದೇ ಆದ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿದೆ, ಮತ್ತು ಪರಿಹಾರದ ಕೆಲವು ಭಾಗಗಳನ್ನು ಹೆಚ್ಚು ಕಟ್ಟುನಿಟ್ಟಾದ ಶೈಕ್ಷಣಿಕ ಶೈಲಿಯಲ್ಲಿ ಇರಿಸಿಕೊಳ್ಳಲು ಸಲಹೆ ನೀಡಲಾಗುತ್ತದೆ:

ಉದಾಹರಣೆ 6

ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಹುಡುಕಿ

ಪರಿಹಾರ

ಸಹಜವಾಗಿ, ಅಸಾಧಾರಣವಾದ ಮೊದಲ ಕಾಲಮ್ ಅನ್ನು ದೊಡ್ಡದಾಗಿ ಮಾಡೋಣ:

ಮತ್ತು, ಕ್ವಾಡ್ರಾಟಿಕ್ ಟ್ರಿನೊಮಿಯಲ್ ಅನ್ನು ಅಪವರ್ತಿಸಿದ ನಂತರ:

ಪರಿಣಾಮವಾಗಿ, ಐಜೆನ್ವಾಲ್ಯೂಗಳನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ, ಅವುಗಳಲ್ಲಿ ಎರಡು ಗುಣಾಕಾರಗಳಾಗಿವೆ.

ಈಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

1) "ಸರಳೀಕೃತ" ಯೋಜನೆಯ ಪ್ರಕಾರ ಒಂಟಿ ಸೈನಿಕನೊಂದಿಗೆ ವ್ಯವಹರಿಸೋಣ:

ಕೊನೆಯ ಎರಡು ಸಮೀಕರಣಗಳಿಂದ, ಸಮಾನತೆಯು ಸ್ಪಷ್ಟವಾಗಿ ಗೋಚರಿಸುತ್ತದೆ, ಇದು ನಿಸ್ಸಂಶಯವಾಗಿ, ವ್ಯವಸ್ಥೆಯ 1 ನೇ ಸಮೀಕರಣಕ್ಕೆ ಬದಲಿಯಾಗಬೇಕು:

ನೀವು ಉತ್ತಮ ಸಂಯೋಜನೆಯನ್ನು ಕಾಣುವುದಿಲ್ಲ:
ಐಜೆನ್ವೆಕ್ಟರ್:

2-3) ಈಗ ನಾವು ಒಂದೆರಡು ಸೆಂಟ್ರಿಗಳನ್ನು ತೆಗೆದುಹಾಕುತ್ತೇವೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ ಅದು ಹೊರಹೊಮ್ಮಬಹುದು ಎರಡು ಅಥವಾ ಒಂದುಐಜೆನ್ವೆಕ್ಟರ್. ಬೇರುಗಳ ಬಹುಸಂಖ್ಯೆಯ ಹೊರತಾಗಿಯೂ, ನಾವು ಮೌಲ್ಯವನ್ನು ನಿರ್ಣಾಯಕಕ್ಕೆ ಬದಲಿಸುತ್ತೇವೆ ಅದು ನಮಗೆ ಮುಂದಿನದನ್ನು ತರುತ್ತದೆ ರೇಖೀಯ ಸಮೀಕರಣಗಳ ಏಕರೂಪದ ವ್ಯವಸ್ಥೆ:

ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು ನಿಖರವಾಗಿ ವೆಕ್ಟರ್ಗಳಾಗಿವೆ
ಪರಿಹಾರಗಳ ಮೂಲಭೂತ ವ್ಯವಸ್ಥೆ

ವಾಸ್ತವವಾಗಿ, ಇಡೀ ಪಾಠದ ಉದ್ದಕ್ಕೂ ನಾವು ಮೂಲಭೂತ ವ್ಯವಸ್ಥೆಯ ವಾಹಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದನ್ನು ಹೊರತುಪಡಿಸಿ ಏನನ್ನೂ ಮಾಡಲಿಲ್ಲ. ಸದ್ಯಕ್ಕೆ ಈ ಪದವು ವಿಶೇಷವಾಗಿ ಅಗತ್ಯವಿರಲಿಲ್ಲ. ಅಂದಹಾಗೆ, ಮರೆಮಾಚುವ ಸೂಟ್‌ಗಳಲ್ಲಿ ವಿಷಯವನ್ನು ತಪ್ಪಿಸಿಕೊಂಡ ಬುದ್ಧಿವಂತ ವಿದ್ಯಾರ್ಥಿಗಳು ಏಕರೂಪದ ಸಮೀಕರಣಗಳು, ಈಗ ಅದನ್ನು ಧೂಮಪಾನ ಮಾಡಲು ಒತ್ತಾಯಿಸಲಾಗುತ್ತದೆ.

ಹೆಚ್ಚುವರಿ ಸಾಲುಗಳನ್ನು ತೆಗೆದುಹಾಕುವುದು ಮಾತ್ರ ಕ್ರಮವಾಗಿದೆ. ಫಲಿತಾಂಶವು ಮಧ್ಯದಲ್ಲಿ ಔಪಚಾರಿಕ "ಹಂತ" ದೊಂದಿಗೆ ಒಂದು-ಮೂರು-ಮೂರು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ.
- ಮೂಲ ವೇರಿಯಬಲ್, - ಉಚಿತ ಅಸ್ಥಿರ. ಆದ್ದರಿಂದ ಎರಡು ಉಚಿತ ಅಸ್ಥಿರಗಳಿವೆ ಮೂಲಭೂತ ವ್ಯವಸ್ಥೆಯ ಎರಡು ವಾಹಕಗಳು ಸಹ ಇವೆ.

ಉಚಿತ ಅಸ್ಥಿರಗಳ ವಿಷಯದಲ್ಲಿ ಮೂಲಭೂತ ವೇರಿಯಬಲ್ ಅನ್ನು ವ್ಯಕ್ತಪಡಿಸೋಣ: . "X" ನ ಮುಂದೆ ಶೂನ್ಯ ಗುಣಕವು ಸಂಪೂರ್ಣವಾಗಿ ಯಾವುದೇ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಲು ಅನುಮತಿಸುತ್ತದೆ (ಇದು ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯಿಂದ ಸ್ಪಷ್ಟವಾಗಿ ಗೋಚರಿಸುತ್ತದೆ).

ಈ ಸಮಸ್ಯೆಯ ಸಂದರ್ಭದಲ್ಲಿ, ಸಾಮಾನ್ಯ ಪರಿಹಾರವನ್ನು ಸತತವಾಗಿ ಬರೆಯಲು ಹೆಚ್ಚು ಅನುಕೂಲಕರವಾಗಿದೆ, ಆದರೆ ಒಂದು ಕಾಲಮ್ನಲ್ಲಿ:

ಜೋಡಿಯು ಐಜೆನ್ವೆಕ್ಟರ್ಗೆ ಅನುರೂಪವಾಗಿದೆ:
ಜೋಡಿಯು ಐಜೆನ್ವೆಕ್ಟರ್ಗೆ ಅನುರೂಪವಾಗಿದೆ:

ಸೂಚನೆ : ಅತ್ಯಾಧುನಿಕ ಓದುಗರು ಈ ವೆಕ್ಟರ್‌ಗಳನ್ನು ಮೌಖಿಕವಾಗಿ ಆಯ್ಕೆ ಮಾಡಬಹುದು - ಸರಳವಾಗಿ ಸಿಸ್ಟಮ್ ಅನ್ನು ವಿಶ್ಲೇಷಿಸುವ ಮೂಲಕ , ಆದರೆ ಇಲ್ಲಿ ಕೆಲವು ಜ್ಞಾನದ ಅಗತ್ಯವಿದೆ: ಮೂರು ಅಸ್ಥಿರಗಳಿವೆ, ಸಿಸ್ಟಮ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಶ್ರೇಣಿ- ಒಂದು, ಅಂದರೆ ಮೂಲಭೂತ ನಿರ್ಧಾರ ವ್ಯವಸ್ಥೆ 3 - 1 = 2 ವೆಕ್ಟರ್‌ಗಳನ್ನು ಒಳಗೊಂಡಿದೆ. ಆದಾಗ್ಯೂ, ಕಂಡುಬರುವ ವಾಹಕಗಳು ಈ ಜ್ಞಾನವಿಲ್ಲದೆ, ಸಂಪೂರ್ಣವಾಗಿ ಅರ್ಥಗರ್ಭಿತ ಮಟ್ಟದಲ್ಲಿ ಸ್ಪಷ್ಟವಾಗಿ ಗೋಚರಿಸುತ್ತವೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಮೂರನೇ ವೆಕ್ಟರ್ ಅನ್ನು ಇನ್ನಷ್ಟು "ಸುಂದರವಾಗಿ" ಬರೆಯಲಾಗುತ್ತದೆ: . ಆದಾಗ್ಯೂ, ಇನ್ನೊಂದು ಉದಾಹರಣೆಯಲ್ಲಿ, ಸರಳವಾದ ಆಯ್ಕೆಯು ಸಾಧ್ಯವಾಗದಿರಬಹುದು ಎಂದು ನಾನು ನಿಮಗೆ ಎಚ್ಚರಿಸುತ್ತೇನೆ, ಅದಕ್ಕಾಗಿಯೇ ಷರತ್ತು ಅನುಭವಿ ಜನರಿಗೆ ಉದ್ದೇಶಿಸಲಾಗಿದೆ. ಹೆಚ್ಚುವರಿಯಾಗಿ, ಮೂರನೇ ವೆಕ್ಟರ್ ಎಂದು ಏಕೆ ತೆಗೆದುಕೊಳ್ಳಬಾರದು? ಎಲ್ಲಾ ನಂತರ, ಅದರ ನಿರ್ದೇಶಾಂಕಗಳು ಸಿಸ್ಟಮ್ನ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣವನ್ನು ಮತ್ತು ವೆಕ್ಟರ್ಗಳನ್ನು ಸಹ ಪೂರೈಸುತ್ತವೆ ರೇಖೀಯವಾಗಿ ಸ್ವತಂತ್ರ. ಈ ಆಯ್ಕೆಯು ತಾತ್ವಿಕವಾಗಿ ಸೂಕ್ತವಾಗಿದೆ, ಆದರೆ "ವಕ್ರ", ಏಕೆಂದರೆ "ಇತರ" ವೆಕ್ಟರ್ ಮೂಲಭೂತ ವ್ಯವಸ್ಥೆಯ ವಾಹಕಗಳ ರೇಖೀಯ ಸಂಯೋಜನೆಯಾಗಿದೆ.

ಉತ್ತರ: eigenvalues:, eigenvectors:

ಸ್ವತಂತ್ರ ಪರಿಹಾರಕ್ಕಾಗಿ ಇದೇ ಉದಾಹರಣೆ:

ಉದಾಹರಣೆ 7

ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಹುಡುಕಿ

ಪಾಠದ ಕೊನೆಯಲ್ಲಿ ಅಂತಿಮ ವಿನ್ಯಾಸದ ಅಂದಾಜು ಮಾದರಿ.

6 ನೇ ಮತ್ತು 7 ನೇ ಉದಾಹರಣೆಗಳಲ್ಲಿ ರೇಖೀಯ ಸ್ವತಂತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳ ಟ್ರಿಪಲ್ ಅನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಆದ್ದರಿಂದ ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಅಂಗೀಕೃತ ವಿಭಜನೆಯಲ್ಲಿ ಪ್ರತಿನಿಧಿಸಲಾಗುತ್ತದೆ ಎಂದು ಗಮನಿಸಬೇಕು. ಆದರೆ ಅಂತಹ ರಾಸ್್ಬೆರ್ರಿಸ್ ಎಲ್ಲಾ ಸಂದರ್ಭಗಳಲ್ಲಿ ಸಂಭವಿಸುವುದಿಲ್ಲ:

ಉದಾಹರಣೆ 8

ಪರಿಹಾರ: ವಿಶಿಷ್ಟ ಸಮೀಕರಣವನ್ನು ರಚಿಸೋಣ ಮತ್ತು ಪರಿಹರಿಸೋಣ:

ಮೊದಲ ಅಂಕಣದಲ್ಲಿ ನಿರ್ಣಾಯಕವನ್ನು ವಿಸ್ತರಿಸೋಣ:

ಪರಿಗಣಿಸಲಾದ ವಿಧಾನದ ಪ್ರಕಾರ ನಾವು ಮತ್ತಷ್ಟು ಸರಳೀಕರಣಗಳನ್ನು ಕೈಗೊಳ್ಳುತ್ತೇವೆ, ಮೂರನೇ ಹಂತದ ಬಹುಪದವನ್ನು ತಪ್ಪಿಸುತ್ತೇವೆ:

- ಸಮಾನ ಮೌಲ್ಯಗಳು.

ಈಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

1) ಮೂಲದಲ್ಲಿ ಯಾವುದೇ ತೊಂದರೆಗಳಿಲ್ಲ:

ಆಶ್ಚರ್ಯಪಡಬೇಡಿ, ಕಿಟ್ ಜೊತೆಗೆ, ಬಳಕೆಯಲ್ಲಿ ಅಸ್ಥಿರಗಳು ಸಹ ಇವೆ - ಇಲ್ಲಿ ಯಾವುದೇ ವ್ಯತ್ಯಾಸವಿಲ್ಲ.

3 ನೇ ಸಮೀಕರಣದಿಂದ ನಾವು ಅದನ್ನು ವ್ಯಕ್ತಪಡಿಸುತ್ತೇವೆ ಮತ್ತು ಅದನ್ನು 1 ನೇ ಮತ್ತು 2 ನೇ ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸುತ್ತೇವೆ:

ಎರಡೂ ಸಮೀಕರಣಗಳಿಂದ ಇದು ಅನುಸರಿಸುತ್ತದೆ:

ನಂತರ ಅವಕಾಶ:

2-3) ಬಹು ಮೌಲ್ಯಗಳಿಗಾಗಿ ನಾವು ಸಿಸ್ಟಮ್ ಅನ್ನು ಪಡೆಯುತ್ತೇವೆ .

ಸಿಸ್ಟಮ್ನ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಬರೆಯೋಣ ಮತ್ತು ಪ್ರಾಥಮಿಕ ರೂಪಾಂತರಗಳನ್ನು ಬಳಸಿ, ಅದನ್ನು ಹಂತ ಹಂತವಾಗಿ ರೂಪಕ್ಕೆ ತರೋಣ:

www.siteಹುಡುಕಲು ನಿಮಗೆ ಅನುಮತಿಸುತ್ತದೆ. ಸೈಟ್ ಲೆಕ್ಕಾಚಾರವನ್ನು ನಿರ್ವಹಿಸುತ್ತದೆ. ಕೆಲವು ಸೆಕೆಂಡುಗಳಲ್ಲಿ ಸರ್ವರ್ ಸರಿಯಾದ ಪರಿಹಾರವನ್ನು ನೀಡುತ್ತದೆ. ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗೆ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಡಿಟರ್ಮಿನೆಂಟ್ ಅನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ನಿಯಮವನ್ನು ಬಳಸಿಕೊಂಡು ಕಂಡುಬರುವ ಬೀಜಗಣಿತದ ಅಭಿವ್ಯಕ್ತಿಯಾಗಿದೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್, ಮುಖ್ಯ ಕರ್ಣೀಯ ಉದ್ದಕ್ಕೂ ಕರ್ಣೀಯ ಅಂಶಗಳು ಮತ್ತು ವೇರಿಯಬಲ್ ಮೌಲ್ಯಗಳಲ್ಲಿ ವ್ಯತ್ಯಾಸಗಳಿರುತ್ತವೆ. ಲೆಕ್ಕಾಚಾರ ಮಾಡುವಾಗ ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ, ಪ್ರತಿ ಅಂಶ ಮ್ಯಾಟ್ರಿಕ್ಸ್ಅನುಗುಣವಾದ ಇತರ ಅಂಶಗಳೊಂದಿಗೆ ಗುಣಿಸಲಾಗುವುದು ಮ್ಯಾಟ್ರಿಕ್ಸ್. ಮೋಡ್‌ನಲ್ಲಿ ಹುಡುಕಿ ಆನ್ಲೈನ್ಚೌಕಕ್ಕೆ ಮಾತ್ರ ಸಾಧ್ಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್. ಕಾರ್ಯಾಚರಣೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಅಂಶಗಳ ಉತ್ಪನ್ನದ ಬೀಜಗಣಿತದ ಮೊತ್ತವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಕಡಿಮೆ ಮಾಡುತ್ತದೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ನಿರ್ಣಾಯಕವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಪರಿಣಾಮವಾಗಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್, ನಿರ್ಧರಿಸುವ ಉದ್ದೇಶಕ್ಕಾಗಿ ಮಾತ್ರ ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ. ಈ ಕಾರ್ಯಾಚರಣೆಯು ಸಿದ್ಧಾಂತದಲ್ಲಿ ವಿಶೇಷ ಸ್ಥಾನವನ್ನು ಪಡೆದುಕೊಂಡಿದೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್, ಬೇರುಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ಮತ್ತು ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಹಿಡಿಯಲು ನಿಮಗೆ ಅನುಮತಿಸುತ್ತದೆ. ಹುಡುಕುವ ಕಾರ್ಯ ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಗುಣಿಸುವ ಅಂಶಗಳನ್ನು ಒಳಗೊಂಡಿದೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ಒಂದು ನಿರ್ದಿಷ್ಟ ನಿಯಮದ ಪ್ರಕಾರ ಈ ಉತ್ಪನ್ನಗಳನ್ನು ಒಟ್ಟುಗೂಡಿಸುವ ಮೂಲಕ ಅನುಸರಿಸಲಾಗುತ್ತದೆ. www.siteಕಂಡುಕೊಳ್ಳುತ್ತಾನೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗೆ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಕ್ರಮದಲ್ಲಿ ಆಯಾಮವನ್ನು ನೀಡಲಾಗಿದೆ ಆನ್ಲೈನ್. ಲೆಕ್ಕಾಚಾರ ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಅದರ ಆಯಾಮವನ್ನು ನೀಡಿದರೆ, ಇದು ಸಂಖ್ಯಾತ್ಮಕ ಅಥವಾ ಸಾಂಕೇತಿಕ ಗುಣಾಂಕಗಳೊಂದಿಗೆ ಬಹುಪದವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು, ನಿರ್ಣಾಯಕವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ನಿಯಮದ ಪ್ರಕಾರ ಕಂಡುಬರುತ್ತದೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್- ಅನುಗುಣವಾದ ಅಂಶಗಳ ಉತ್ಪನ್ನಗಳ ಮೊತ್ತವಾಗಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್, ನಿರ್ಧರಿಸುವ ಉದ್ದೇಶಕ್ಕಾಗಿ ಮಾತ್ರ ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ. ಕ್ವಾಡ್ರಾಟಿಕ್‌ಗಾಗಿ ವೇರಿಯಬಲ್‌ಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಬಹುಪದವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಮ್ಯಾಟ್ರಿಕ್ಸ್, ವ್ಯಾಖ್ಯಾನದಂತೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗೆ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ, ಸಿದ್ಧಾಂತದಲ್ಲಿ ಸಾಮಾನ್ಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್. ಬಹುಪದದ ಬೇರುಗಳ ಅರ್ಥ ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು ಮತ್ತು ಐಜೆನ್‌ವಾಲ್ಯೂಗಳನ್ನು ನಿರ್ಧರಿಸಲು ಬಳಸಲಾಗುತ್ತದೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್. ಇದಲ್ಲದೆ, ನಿರ್ಣಾಯಕ ವೇಳೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ನಂತರ ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ವಿಶಿಷ್ಟ ಸಮೀಕರಣರಿವರ್ಸ್‌ಗಿಂತ ಭಿನ್ನವಾಗಿ ಇನ್ನೂ ಅಸ್ತಿತ್ವದಲ್ಲಿರುತ್ತದೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್. ಲೆಕ್ಕ ಹಾಕುವ ಸಲುವಾಗಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗೆ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಅಥವಾ ಏಕಕಾಲದಲ್ಲಿ ಹಲವಾರು ಹುಡುಕಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಗಳು, ನೀವು ಸಾಕಷ್ಟು ಸಮಯ ಮತ್ತು ಶ್ರಮವನ್ನು ವ್ಯಯಿಸಬೇಕಾಗಿದೆ, ಆದರೆ ನಮ್ಮ ಸರ್ವರ್ ಕೆಲವೇ ಸೆಕೆಂಡುಗಳಲ್ಲಿ ಕಂಡುಕೊಳ್ಳುತ್ತದೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆನ್‌ಲೈನ್‌ಗೆ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಕಂಡುಹಿಡಿಯುವ ಉತ್ತರ ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಕಂಡುಹಿಡಿಯುವಾಗ ಸಂಖ್ಯೆಗಳು ಸಹ ಸರಿಯಾಗಿ ಮತ್ತು ಸಾಕಷ್ಟು ನಿಖರತೆಯೊಂದಿಗೆ ಇರುತ್ತದೆ ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ವಿಶಿಷ್ಟ ಸಮೀಕರಣತರ್ಕಹೀನವಾಗಿರುತ್ತದೆ. ಸೈಟ್ನಲ್ಲಿ www.siteಅಂಶಗಳಲ್ಲಿ ಅಕ್ಷರ ನಮೂದುಗಳನ್ನು ಅನುಮತಿಸಲಾಗಿದೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್, ಅದು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆನ್‌ಲೈನ್‌ಗೆ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಲೆಕ್ಕಾಚಾರ ಮಾಡುವಾಗ ಸಾಮಾನ್ಯ ಸಾಂಕೇತಿಕ ರೂಪದಲ್ಲಿ ಪ್ರತಿನಿಧಿಸಬಹುದು ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ. ಕಂಡುಹಿಡಿಯುವ ಸಮಸ್ಯೆಯನ್ನು ಪರಿಹರಿಸುವಾಗ ಪಡೆದ ಉತ್ತರವನ್ನು ಪರಿಶೀಲಿಸಲು ಇದು ಉಪಯುಕ್ತವಾಗಿದೆ ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಸೈಟ್ ಅನ್ನು ಬಳಸುವುದು www.site. ಬಹುಪದವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ಕಾರ್ಯಾಚರಣೆಯನ್ನು ನಿರ್ವಹಿಸುವಾಗ - ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ, ಈ ಸಮಸ್ಯೆಯನ್ನು ಪರಿಹರಿಸುವಾಗ ನೀವು ಜಾಗರೂಕರಾಗಿರಬೇಕು ಮತ್ತು ಹೆಚ್ಚು ಗಮನಹರಿಸಬೇಕು. ಪ್ರತಿಯಾಗಿ, ವಿಷಯದ ಕುರಿತು ನಿಮ್ಮ ನಿರ್ಧಾರವನ್ನು ಪರಿಶೀಲಿಸಲು ನಮ್ಮ ಸೈಟ್ ನಿಮಗೆ ಸಹಾಯ ಮಾಡುತ್ತದೆ ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ. ಪರಿಹರಿಸಿದ ಸಮಸ್ಯೆಗಳ ದೀರ್ಘ ತಪಾಸಣೆಗಾಗಿ ನಿಮಗೆ ಸಮಯವಿಲ್ಲದಿದ್ದರೆ, ಆಗ www.siteಕಂಡುಹಿಡಿಯುವಾಗ ಮತ್ತು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವಾಗ ಪರಿಶೀಲಿಸಲು ಖಂಡಿತವಾಗಿಯೂ ಅನುಕೂಲಕರ ಸಾಧನವಾಗಿದೆ ಆನ್‌ಲೈನ್‌ನಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ.

ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್‌ವೆಕ್ಟರ್ ಒಂದು, ಕೊಟ್ಟಿರುವ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನಿಂದ ಗುಣಿಸಿದಾಗ, ಕೊಲಿನಿಯರ್ ವೆಕ್ಟರ್‌ಗೆ ಕಾರಣವಾಗುತ್ತದೆ. ಸರಳವಾಗಿ ಹೇಳುವುದಾದರೆ, ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಐಜೆನ್ವೆಕ್ಟರ್ನಿಂದ ಗುಣಿಸಿದಾಗ, ಎರಡನೆಯದು ಒಂದೇ ಆಗಿರುತ್ತದೆ, ಆದರೆ ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯಿಂದ ಗುಣಿಸಲ್ಪಡುತ್ತದೆ.

ವ್ಯಾಖ್ಯಾನ

ಐಜೆನ್ವೆಕ್ಟರ್ ಶೂನ್ಯವಲ್ಲದ ವೆಕ್ಟರ್ V ಆಗಿದೆ, ಇದು ಒಂದು ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ M ನಿಂದ ಗುಣಿಸಿದಾಗ, ಕೆಲವು ಸಂಖ್ಯೆ λ ನಿಂದ ಸ್ವತಃ ಹೆಚ್ಚಾಗುತ್ತದೆ. ಬೀಜಗಣಿತದ ಸಂಕೇತದಲ್ಲಿ ಇದು ಈ ರೀತಿ ಕಾಣುತ್ತದೆ:

M × V = λ × V,

ಇಲ್ಲಿ λ ಎಂಬುದು ಮ್ಯಾಟ್ರಿಕ್ಸ್ M ನ ಐಜೆನ್‌ವಾಲ್ಯೂ ಆಗಿದೆ.

ಸಂಖ್ಯಾತ್ಮಕ ಉದಾಹರಣೆಯನ್ನು ನೋಡೋಣ. ರೆಕಾರ್ಡಿಂಗ್ ಸುಲಭವಾಗುವಂತೆ, ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನಲ್ಲಿರುವ ಸಂಖ್ಯೆಗಳನ್ನು ಅರ್ಧವಿರಾಮ ಚಿಹ್ನೆಯಿಂದ ಬೇರ್ಪಡಿಸಲಾಗುತ್ತದೆ. ನಾವು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಹೊಂದೋಣ:

• M = 0; 4;
• 6; 10.

ಅದನ್ನು ಕಾಲಮ್ ವೆಕ್ಟರ್ ಮೂಲಕ ಗುಣಿಸೋಣ:

• ವಿ = -2;

ನಾವು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಕಾಲಮ್ ವೆಕ್ಟರ್‌ನಿಂದ ಗುಣಿಸಿದಾಗ, ನಾವು ಕಾಲಮ್ ವೆಕ್ಟರ್ ಅನ್ನು ಸಹ ಪಡೆಯುತ್ತೇವೆ. ಕಟ್ಟುನಿಟ್ಟಾದ ಗಣಿತದ ಭಾಷೆಯಲ್ಲಿ, ಕಾಲಮ್ ವೆಕ್ಟರ್‌ನಿಂದ 2 × 2 ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಗುಣಿಸುವ ಸೂತ್ರವು ಈ ರೀತಿ ಕಾಣುತ್ತದೆ:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 ಎಂದರೆ ಮೊದಲ ಸಾಲು ಮತ್ತು ಮೊದಲ ಕಾಲಮ್‌ನಲ್ಲಿರುವ ಮ್ಯಾಟ್ರಿಕ್ಸ್ M ನ ಅಂಶ, ಮತ್ತು M22 ಎಂದರೆ ಎರಡನೇ ಸಾಲು ಮತ್ತು ಎರಡನೇ ಕಾಲಮ್‌ನಲ್ಲಿರುವ ಅಂಶ. ನಮ್ಮ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗೆ, ಈ ಅಂಶಗಳು M11 = 0, M12 = 4, M21 = 6, M22 10 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಕಾಲಮ್ ವೆಕ್ಟರ್‌ಗೆ, ಈ ಮೌಲ್ಯಗಳು V11 = –2, V21 = 1. ಈ ಸೂತ್ರದ ಪ್ರಕಾರ, ವೆಕ್ಟರ್‌ನಿಂದ ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಉತ್ಪನ್ನದ ಕೆಳಗಿನ ಫಲಿತಾಂಶವನ್ನು ನಾವು ಪಡೆಯುತ್ತೇವೆ:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

ಅನುಕೂಲಕ್ಕಾಗಿ, ಕಾಲಮ್ ವೆಕ್ಟರ್ ಅನ್ನು ಸಾಲಾಗಿ ಬರೆಯೋಣ. ಆದ್ದರಿಂದ, ನಾವು ಸ್ಕ್ವೇರ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ವೆಕ್ಟರ್ (-2; 1) ಮೂಲಕ ಗುಣಿಸಿದ್ದೇವೆ, ಇದರ ಪರಿಣಾಮವಾಗಿ ವೆಕ್ಟರ್ (4; -2). ನಿಸ್ಸಂಶಯವಾಗಿ, ಇದು λ = -2 ರಿಂದ ಗುಣಿಸಿದ ಅದೇ ವೆಕ್ಟರ್ ಆಗಿದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ ಲ್ಯಾಂಬ್ಡಾ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್‌ವಾಲ್ಯೂ ಅನ್ನು ಸೂಚಿಸುತ್ತದೆ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್ವೆಕ್ಟರ್ ಒಂದು ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್ ಆಗಿದೆ, ಅಂದರೆ, ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನಿಂದ ಗುಣಿಸಿದಾಗ ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ತನ್ನ ಸ್ಥಾನವನ್ನು ಬದಲಾಯಿಸದ ವಸ್ತು. ವೆಕ್ಟರ್ ಬೀಜಗಣಿತದಲ್ಲಿ ಕೋಲಿನಿಯರಿಟಿಯ ಪರಿಕಲ್ಪನೆಯು ಜ್ಯಾಮಿತಿಯಲ್ಲಿ ಸಮಾನಾಂತರತೆಯ ಪದವನ್ನು ಹೋಲುತ್ತದೆ. ಜ್ಯಾಮಿತೀಯ ವ್ಯಾಖ್ಯಾನದಲ್ಲಿ, ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್‌ಗಳು ವಿಭಿನ್ನ ಉದ್ದಗಳ ಸಮಾನಾಂತರ ನಿರ್ದೇಶಿತ ವಿಭಾಗಗಳಾಗಿವೆ. ಯೂಕ್ಲಿಡ್‌ನ ಕಾಲದಿಂದಲೂ, ಒಂದು ರೇಖೆಯು ಅನಂತ ಸಂಖ್ಯೆಯ ಸಾಲುಗಳನ್ನು ಸಮಾನಾಂತರವಾಗಿ ಹೊಂದಿದೆ ಎಂದು ನಮಗೆ ತಿಳಿದಿದೆ, ಆದ್ದರಿಂದ ಪ್ರತಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನಂತ ಸಂಖ್ಯೆಯ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಹೊಂದಿದೆ ಎಂದು ಭಾವಿಸುವುದು ತಾರ್ಕಿಕವಾಗಿದೆ.

ಹಿಂದಿನ ಉದಾಹರಣೆಯಿಂದ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು (-8; 4), ಮತ್ತು (16; -8), ಮತ್ತು (32, -16) ಆಗಿರಬಹುದು ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ. ಇವೆಲ್ಲವೂ ಈಜೆನ್‌ವಾಲ್ಯೂ λ = -2 ಗೆ ಅನುಗುಣವಾದ ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್‌ಗಳಾಗಿವೆ. ಈ ವೆಕ್ಟರ್‌ಗಳಿಂದ ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಗುಣಿಸಿದಾಗ, ನಾವು ಇನ್ನೂ 2 ಬಾರಿ ಮೂಲದಿಂದ ಭಿನ್ನವಾಗಿರುವ ವೆಕ್ಟರ್‌ನೊಂದಿಗೆ ಕೊನೆಗೊಳ್ಳುತ್ತೇವೆ. ಅದಕ್ಕಾಗಿಯೇ, ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸುವಾಗ, ರೇಖಾತ್ಮಕವಾಗಿ ಸ್ವತಂತ್ರ ವೆಕ್ಟರ್ ವಸ್ತುಗಳನ್ನು ಮಾತ್ರ ಕಂಡುಹಿಡಿಯುವುದು ಅವಶ್ಯಕ. ಹೆಚ್ಚಾಗಿ, n × n ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗೆ, n ಸಂಖ್ಯೆಯ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳಿರುತ್ತವೆ. ನಮ್ಮ ಕ್ಯಾಲ್ಕುಲೇಟರ್ ಅನ್ನು ಎರಡನೇ ಕ್ರಮಾಂಕದ ಚದರ ಮ್ಯಾಟ್ರಿಸಸ್‌ಗಳ ವಿಶ್ಲೇಷಣೆಗಾಗಿ ವಿನ್ಯಾಸಗೊಳಿಸಲಾಗಿದೆ, ಆದ್ದರಿಂದ ಫಲಿತಾಂಶವು ಯಾವಾಗಲೂ ಎರಡು ಐಜೆನ್‌ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಕೊಳ್ಳುತ್ತದೆ, ಅವುಗಳು ಹೊಂದಿಕೆಯಾಗುವ ಸಂದರ್ಭಗಳನ್ನು ಹೊರತುಪಡಿಸಿ.

ಮೇಲಿನ ಉದಾಹರಣೆಯಲ್ಲಿ, ನಾವು ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಮುಂಚಿತವಾಗಿ ತಿಳಿದಿದ್ದೇವೆ ಮತ್ತು ಲ್ಯಾಂಬ್ಡಾ ಸಂಖ್ಯೆಯನ್ನು ಸ್ಪಷ್ಟವಾಗಿ ನಿರ್ಧರಿಸಿದ್ದೇವೆ. ಆದಾಗ್ಯೂ, ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಎಲ್ಲವೂ ಬೇರೆ ರೀತಿಯಲ್ಲಿ ನಡೆಯುತ್ತದೆ: ಐಜೆನ್ವಾಲ್ಯೂಗಳು ಮೊದಲು ಕಂಡುಬರುತ್ತವೆ ಮತ್ತು ನಂತರ ಮಾತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು.

ಪರಿಹಾರ ಅಲ್ಗಾರಿದಮ್

ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್ M ಅನ್ನು ಮತ್ತೊಮ್ಮೆ ನೋಡೋಣ ಮತ್ತು ಅದರ ಎರಡೂ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳನ್ನು ಕಂಡುಹಿಡಿಯಲು ಪ್ರಯತ್ನಿಸೋಣ. ಆದ್ದರಿಂದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಈ ರೀತಿ ಕಾಣುತ್ತದೆ:

• M = 0; 4;
• 6; 10.

ಮೊದಲು ನಾವು ಈಜೆನ್‌ವಾಲ್ಯೂ λ ಅನ್ನು ನಿರ್ಧರಿಸಬೇಕು, ಇದಕ್ಕೆ ಈ ಕೆಳಗಿನ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ನಿರ್ಣಾಯಕವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ಅಗತ್ಯವಿದೆ:

• (0 - λ); 4;
• 6; (10 - λ).

ಮುಖ್ಯ ಕರ್ಣೀಯ ಅಂಶಗಳಿಂದ ಅಜ್ಞಾತ λ ಅನ್ನು ಕಳೆಯುವ ಮೂಲಕ ಈ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ. ಪ್ರಮಾಣಿತ ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ನಿರ್ಣಾಯಕವನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ:

• detA = M11 × M21 - M12 × M22
• detA = (0 - λ) × (10 - λ) - 24

ನಮ್ಮ ವೆಕ್ಟರ್ ಶೂನ್ಯವಲ್ಲದ ಕಾರಣ, ನಾವು ಫಲಿತಾಂಶದ ಸಮೀಕರಣವನ್ನು ರೇಖೀಯವಾಗಿ ಅವಲಂಬಿತವಾಗಿ ಸ್ವೀಕರಿಸುತ್ತೇವೆ ಮತ್ತು ನಮ್ಮ ನಿರ್ಣಾಯಕ detA ಅನ್ನು ಶೂನ್ಯಕ್ಕೆ ಸಮೀಕರಿಸುತ್ತೇವೆ.

(0 - λ) × (10 - λ) - 24 = 0

ಬ್ರಾಕೆಟ್‌ಗಳನ್ನು ತೆರೆಯೋಣ ಮತ್ತು ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ವಿಶಿಷ್ಟ ಸಮೀಕರಣವನ್ನು ಪಡೆಯೋಣ:

λ 2 - 10λ - 24 = 0

ಇದು ಪ್ರಮಾಣಿತ ಕ್ವಾಡ್ರಾಟಿಕ್ ಸಮೀಕರಣವಾಗಿದ್ದು, ಇದನ್ನು ತಾರತಮ್ಯವನ್ನು ಬಳಸಿಕೊಂಡು ಪರಿಹರಿಸಬೇಕಾಗಿದೆ.

D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

ತಾರತಮ್ಯದ ಮೂಲವು sqrt(D) = 14, ಆದ್ದರಿಂದ λ1 = -2, λ2 = 12. ಈಗ ಪ್ರತಿ ಲ್ಯಾಂಬ್ಡಾ ಮೌಲ್ಯಕ್ಕೆ ನಾವು ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕು. ನಾವು λ = -2 ಗಾಗಿ ಸಿಸ್ಟಮ್ ಗುಣಾಂಕಗಳನ್ನು ವ್ಯಕ್ತಪಡಿಸೋಣ.

• M - λ × E = 2; 4;
• 6; 12.

ಈ ಸೂತ್ರದಲ್ಲಿ, E ಗುರುತಿನ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ. ಫಲಿತಾಂಶದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಆಧರಿಸಿ, ನಾವು ರೇಖೀಯ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯನ್ನು ರಚಿಸುತ್ತೇವೆ:

2x + 4y = 6x + 12y,

ಇಲ್ಲಿ x ಮತ್ತು y ಐಜೆನ್ವೆಕ್ಟರ್ ಅಂಶಗಳಾಗಿವೆ.

ಎಡಭಾಗದಲ್ಲಿರುವ ಎಲ್ಲಾ X ಮತ್ತು ಬಲಭಾಗದಲ್ಲಿರುವ ಎಲ್ಲಾ Y ಗಳನ್ನು ಸಂಗ್ರಹಿಸೋಣ. ನಿಸ್ಸಂಶಯವಾಗಿ - 4x = 8y. ಅಭಿವ್ಯಕ್ತಿಯನ್ನು - 4 ರಿಂದ ಭಾಗಿಸಿ ಮತ್ತು x = –2y ಪಡೆಯಿರಿ. ಈಗ ನಾವು ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಮೊದಲ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ನಿರ್ಧರಿಸಬಹುದು, ಅಪರಿಚಿತರ ಯಾವುದೇ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು (ರೇಖೀಯವಾಗಿ ಅವಲಂಬಿತ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳ ಅನಂತತೆಯನ್ನು ನೆನಪಿಡಿ). y = 1 ಅನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ, ನಂತರ x = –2. ಆದ್ದರಿಂದ, ಮೊದಲ ಐಜೆನ್ವೆಕ್ಟರ್ V1 = (–2; 1) ನಂತೆ ಕಾಣುತ್ತದೆ. ಲೇಖನದ ಆರಂಭಕ್ಕೆ ಹಿಂತಿರುಗಿ. ಈ ವೆಕ್ಟರ್ ವಸ್ತುವೇ ನಾವು ಐಜೆನ್ವೆಕ್ಟರ್ ಪರಿಕಲ್ಪನೆಯನ್ನು ಪ್ರದರ್ಶಿಸಲು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಗುಣಿಸಿದ್ದೇವೆ.

ಈಗ λ = 12 ಗಾಗಿ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯೋಣ.

• M - λ × E = -12; 4
• 6; -2.

ರೇಖೀಯ ಸಮೀಕರಣಗಳ ಅದೇ ವ್ಯವಸ್ಥೆಯನ್ನು ರಚಿಸೋಣ;

• -12x + 4y = 6x - 2y
• -18x = -6y
• 3x = ವೈ.

ಈಗ ನಾವು x = 1 ಅನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತೇವೆ, ಆದ್ದರಿಂದ y = 3. ಹೀಗಾಗಿ, ಎರಡನೇ ಐಜೆನ್ವೆಕ್ಟರ್ V2 = (1; 3) ನಂತೆ ಕಾಣುತ್ತದೆ. ಕೊಟ್ಟಿರುವ ವೆಕ್ಟರ್‌ನಿಂದ ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಗುಣಿಸಿದಾಗ, ಫಲಿತಾಂಶವು ಯಾವಾಗಲೂ ಅದೇ ವೆಕ್ಟರ್ ಅನ್ನು 12 ರಿಂದ ಗುಣಿಸಿದಾಗ ಇರುತ್ತದೆ. ಇಲ್ಲಿ ಪರಿಹಾರ ಅಲ್ಗಾರಿದಮ್ ಕೊನೆಗೊಳ್ಳುತ್ತದೆ. ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಹಸ್ತಚಾಲಿತವಾಗಿ ಹೇಗೆ ನಿರ್ಧರಿಸುವುದು ಎಂದು ಈಗ ನಿಮಗೆ ತಿಳಿದಿದೆ.

• ನಿರ್ಣಾಯಕ;
• ಜಾಡಿನ, ಅಂದರೆ, ಮುಖ್ಯ ಕರ್ಣೀಯ ಅಂಶಗಳ ಮೊತ್ತ;
• ಶ್ರೇಣಿ, ಅಂದರೆ ರೇಖೀಯ ಸ್ವತಂತ್ರ ಸಾಲುಗಳು/ಕಾಲಮ್‌ಗಳ ಗರಿಷ್ಠ ಸಂಖ್ಯೆ.

ಪ್ರೋಗ್ರಾಂ ಮೇಲಿನ ಅಲ್ಗಾರಿದಮ್ ಪ್ರಕಾರ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ, ಪರಿಹಾರ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಸಾಧ್ಯವಾದಷ್ಟು ಕಡಿಮೆಗೊಳಿಸುತ್ತದೆ. ಪ್ರೋಗ್ರಾಂನಲ್ಲಿ ಲ್ಯಾಂಬ್ಡಾವನ್ನು "ಸಿ" ಅಕ್ಷರದಿಂದ ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ ಎಂದು ಗಮನಿಸುವುದು ಮುಖ್ಯ. ಸಂಖ್ಯಾತ್ಮಕ ಉದಾಹರಣೆಯನ್ನು ನೋಡೋಣ.

ಪ್ರೋಗ್ರಾಂ ಹೇಗೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ ಎಂಬುದರ ಉದಾಹರಣೆ

ಕೆಳಗಿನ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ನಿರ್ಧರಿಸಲು ಪ್ರಯತ್ನಿಸೋಣ:

• M = 5; 13;
• 4; 14.

ಈ ಮೌಲ್ಯಗಳನ್ನು ಕ್ಯಾಲ್ಕುಲೇಟರ್‌ನ ಕೋಶಗಳಲ್ಲಿ ನಮೂದಿಸಿ ಮತ್ತು ಉತ್ತರವನ್ನು ಈ ಕೆಳಗಿನ ರೂಪದಲ್ಲಿ ಪಡೆಯೋಣ:

• ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಶ್ರೇಣಿ: 2;
• ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಡಿಟರ್ಮಿನೆಂಟ್: 18;
• ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಟ್ರೇಸ್: 19;
• ಐಜೆನ್ವೆಕ್ಟರ್ನ ಲೆಕ್ಕಾಚಾರ: c 2 - 19.00c + 18.00 (ವಿಶಿಷ್ಟ ಸಮೀಕರಣ);
• ಐಜೆನ್ವೆಕ್ಟರ್ ಲೆಕ್ಕಾಚಾರ: 18 (ಮೊದಲ ಲ್ಯಾಂಬ್ಡಾ ಮೌಲ್ಯ);
• ಐಜೆನ್ವೆಕ್ಟರ್ ಲೆಕ್ಕಾಚಾರ: 1 (ಎರಡನೇ ಲ್ಯಾಂಬ್ಡಾ ಮೌಲ್ಯ);
• ವೆಕ್ಟರ್ 1 ಗಾಗಿ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆ: -13x1 + 13y1 = 4x1 - 4y1;
• ವೆಕ್ಟರ್ 2 ಗಾಗಿ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆ: 4x1 + 13y1 = 4x1 + 13y1;
• ಐಜೆನ್ವೆಕ್ಟರ್ 1: (1; 1);
• ಐಜೆನ್ವೆಕ್ಟರ್ 2: (-3.25; 1).

ಹೀಗಾಗಿ, ನಾವು ಎರಡು ರೇಖೀಯ ಸ್ವತಂತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳನ್ನು ಪಡೆದುಕೊಂಡಿದ್ದೇವೆ.

ತೀರ್ಮಾನ

ರೇಖೀಯ ಬೀಜಗಣಿತ ಮತ್ತು ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರೇಖಾಗಣಿತವು ಯಾವುದೇ ಹೊಸ ವಿದ್ಯಾರ್ಥಿ ಎಂಜಿನಿಯರಿಂಗ್ ವಿದ್ಯಾರ್ಥಿಗೆ ಪ್ರಮಾಣಿತ ವಿಷಯಗಳಾಗಿವೆ. ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ವಾಹಕಗಳು ಮತ್ತು ಮ್ಯಾಟ್ರಿಸಸ್ ಭಯಾನಕವಾಗಿದೆ, ಮತ್ತು ಅಂತಹ ತೊಡಕಿನ ಲೆಕ್ಕಾಚಾರಗಳಲ್ಲಿ ತಪ್ಪುಗಳನ್ನು ಮಾಡುವುದು ಸುಲಭ. ನಮ್ಮ ಪ್ರೋಗ್ರಾಂ ವಿದ್ಯಾರ್ಥಿಗಳು ತಮ್ಮ ಲೆಕ್ಕಾಚಾರಗಳನ್ನು ಪರಿಶೀಲಿಸಲು ಅಥವಾ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಹುಡುಕುವ ಸಮಸ್ಯೆಯನ್ನು ಸ್ವಯಂಚಾಲಿತವಾಗಿ ಪರಿಹರಿಸಲು ಅನುಮತಿಸುತ್ತದೆ. ನಮ್ಮ ಕ್ಯಾಟಲಾಗ್‌ನಲ್ಲಿ ಇತರ ರೇಖೀಯ ಬೀಜಗಣಿತ ಕ್ಯಾಲ್ಕುಲೇಟರ್‌ಗಳಿವೆ; ಅವುಗಳನ್ನು ನಿಮ್ಮ ಅಧ್ಯಯನ ಅಥವಾ ಕೆಲಸದಲ್ಲಿ ಬಳಸಿ.

"ಮೊದಲ ಭಾಗವು ರಸಾಯನಶಾಸ್ತ್ರವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ಕನಿಷ್ಠ ಅಗತ್ಯವಿರುವ ನಿಬಂಧನೆಗಳನ್ನು ಹೊಂದಿಸುತ್ತದೆ, ಮತ್ತು ಎರಡನೆಯ ಭಾಗವು ಮಲ್ಟಿವೇರಿಯೇಟ್ ವಿಶ್ಲೇಷಣೆಯ ವಿಧಾನಗಳ ಆಳವಾದ ತಿಳುವಳಿಕೆಗಾಗಿ ನೀವು ತಿಳಿದುಕೊಳ್ಳಬೇಕಾದ ಸಂಗತಿಗಳನ್ನು ಒಳಗೊಂಡಿದೆ. ಪ್ರಸ್ತುತಿಯನ್ನು ಎಕ್ಸೆಲ್ ವರ್ಕ್ಬುಕ್ನಲ್ಲಿ ಮಾಡಿದ ಉದಾಹರಣೆಗಳೊಂದಿಗೆ ವಿವರಿಸಲಾಗಿದೆ. Matrix.xls, ಇದು ಈ ಡಾಕ್ಯುಮೆಂಟ್ ಜೊತೆಯಲ್ಲಿದೆ.

ಉದಾಹರಣೆಗಳ ಲಿಂಕ್‌ಗಳನ್ನು ಪಠ್ಯದಲ್ಲಿ ಎಕ್ಸೆಲ್ ಆಬ್ಜೆಕ್ಟ್‌ಗಳಾಗಿ ಇರಿಸಲಾಗಿದೆ. ಈ ಉದಾಹರಣೆಗಳು ಅಮೂರ್ತ ಸ್ವಭಾವವನ್ನು ಹೊಂದಿವೆ; ಅವು ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರಸಾಯನಶಾಸ್ತ್ರದ ಸಮಸ್ಯೆಗಳಿಗೆ ಯಾವುದೇ ರೀತಿಯಲ್ಲಿ ಸಂಬಂಧಿಸಿಲ್ಲ. ರಸಾಯನಶಾಸ್ತ್ರದಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಬೀಜಗಣಿತದ ಬಳಕೆಯ ನೈಜ-ಜೀವನದ ಉದಾಹರಣೆಗಳನ್ನು ವಿವಿಧ ರಸಾಯನಶಾಸ್ತ್ರದ ಅನ್ವಯಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಇತರ ಪಠ್ಯಗಳಲ್ಲಿ ಚರ್ಚಿಸಲಾಗಿದೆ.

ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರಸಾಯನಶಾಸ್ತ್ರದಲ್ಲಿ ಮಾಡಲಾದ ಹೆಚ್ಚಿನ ಅಳತೆಗಳು ನೇರವಲ್ಲ, ಆದರೆ ಪರೋಕ್ಷ. ಇದರರ್ಥ ಪ್ರಯೋಗದಲ್ಲಿ, ಅಪೇಕ್ಷಿತ ವಿಶ್ಲೇಷಕ C (ಸಾಂದ್ರೀಕರಣ) ಮೌಲ್ಯದ ಬದಲಿಗೆ, ಮತ್ತೊಂದು ಮೌಲ್ಯವನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ X(ಸಿಗ್ನಲ್), ಸಂಬಂಧಿತ ಆದರೆ C ಗೆ ಸಮಾನವಾಗಿಲ್ಲ, ಅಂದರೆ. X(C) ≠ C. ನಿಯಮದಂತೆ, ಅವಲಂಬನೆಯ ಪ್ರಕಾರ X(C) ತಿಳಿದಿಲ್ಲ, ಆದರೆ ಅದೃಷ್ಟವಶಾತ್ ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರಸಾಯನಶಾಸ್ತ್ರದಲ್ಲಿ ಹೆಚ್ಚಿನ ಅಳತೆಗಳು ಅನುಪಾತದಲ್ಲಿರುತ್ತವೆ. ಇದರರ್ಥ C ನ ಹೆಚ್ಚುತ್ತಿರುವ ಸಾಂದ್ರತೆಯೊಂದಿಗೆ ಎಬಾರಿ, ಸಂಕೇತ X ಅದೇ ಪ್ರಮಾಣದಲ್ಲಿ ಹೆಚ್ಚಾಗುತ್ತದೆ, ಅಂದರೆ. X(ಎಸಿ) = ಒಂದು x(ಸಿ) ಹೆಚ್ಚುವರಿಯಾಗಿ, ಸಂಕೇತಗಳು ಸಹ ಸಂಯೋಜಕವಾಗಿದೆ, ಆದ್ದರಿಂದ C 1 ಮತ್ತು C 2 ಸಾಂದ್ರತೆಯಿರುವ ಎರಡು ಪದಾರ್ಥಗಳು ಇರುವ ಮಾದರಿಯಿಂದ ಸಂಕೇತವು ಪ್ರತಿ ಘಟಕದಿಂದ ಸಂಕೇತಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ. X(C 1 + C 2) = X(ಸಿ 1)+ X(ಸಿ 2). ಅನುಪಾತ ಮತ್ತು ಸಂಕಲನ ಒಟ್ಟಿಗೆ ನೀಡುತ್ತದೆ ರೇಖೀಯತೆ. ರೇಖೀಯತೆಯ ತತ್ವವನ್ನು ವಿವರಿಸಲು ಅನೇಕ ಉದಾಹರಣೆಗಳನ್ನು ನೀಡಬಹುದು, ಆದರೆ ಎರಡು ಅತ್ಯಂತ ಗಮನಾರ್ಹ ಉದಾಹರಣೆಗಳನ್ನು ನಮೂದಿಸಲು ಸಾಕು - ಕ್ರೊಮ್ಯಾಟೋಗ್ರಫಿ ಮತ್ತು ಸ್ಪೆಕ್ಟ್ರೋಸ್ಕೋಪಿ. ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರಸಾಯನಶಾಸ್ತ್ರದ ಪ್ರಯೋಗದಲ್ಲಿ ಅಂತರ್ಗತವಾಗಿರುವ ಎರಡನೆಯ ವೈಶಿಷ್ಟ್ಯ ಬಹುಚಾನಲ್. ಆಧುನಿಕ ವಿಶ್ಲೇಷಣಾತ್ಮಕ ಉಪಕರಣಗಳು ಏಕಕಾಲದಲ್ಲಿ ಅನೇಕ ಚಾನಲ್‌ಗಳಿಗೆ ಸಂಕೇತಗಳನ್ನು ಅಳೆಯುತ್ತವೆ. ಉದಾಹರಣೆಗೆ, ಬೆಳಕಿನ ಪ್ರಸರಣದ ತೀವ್ರತೆಯನ್ನು ಏಕಕಾಲದಲ್ಲಿ ಹಲವಾರು ತರಂಗಾಂತರಗಳಿಗೆ ಅಳೆಯಲಾಗುತ್ತದೆ, ಅಂದರೆ. ವ್ಯಾಪ್ತಿಯ. ಆದ್ದರಿಂದ, ಪ್ರಯೋಗದಲ್ಲಿ ನಾವು ಅನೇಕ ಸಂಕೇತಗಳೊಂದಿಗೆ ವ್ಯವಹರಿಸುತ್ತೇವೆ X 1 , X 2 ,...., X n, ಅಧ್ಯಯನದ ಅಡಿಯಲ್ಲಿ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಇರುವ ಪದಾರ್ಥಗಳ C 1, C 2, ..., C m ಸಾಂದ್ರತೆಗಳ ಗುಂಪನ್ನು ನಿರೂಪಿಸುತ್ತದೆ.

ಅಕ್ಕಿ. 1 ಸ್ಪೆಕ್ಟ್ರಾ

ಆದ್ದರಿಂದ, ವಿಶ್ಲೇಷಣಾತ್ಮಕ ಪ್ರಯೋಗವನ್ನು ರೇಖಾತ್ಮಕತೆ ಮತ್ತು ಬಹುಆಯಾಮದಿಂದ ನಿರೂಪಿಸಲಾಗಿದೆ. ಆದ್ದರಿಂದ, ಪ್ರಾಯೋಗಿಕ ಡೇಟಾವನ್ನು ವೆಕ್ಟರ್ ಮತ್ತು ಮ್ಯಾಟ್ರಿಸಸ್ ಎಂದು ಪರಿಗಣಿಸಲು ಮತ್ತು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಬೀಜಗಣಿತದ ಉಪಕರಣವನ್ನು ಬಳಸಿಕೊಂಡು ಅವುಗಳನ್ನು ಕುಶಲತೆಯಿಂದ ನಿರ್ವಹಿಸಲು ಅನುಕೂಲಕರವಾಗಿದೆ. ಈ ವಿಧಾನದ ಫಲಪ್ರದತೆಯನ್ನು ತೋರಿಸಿರುವ ಉದಾಹರಣೆಯಿಂದ ವಿವರಿಸಲಾಗಿದೆ, ಇದು 4000 ರಿಂದ 4796 cm -1 ವರೆಗಿನ 200 ತರಂಗಾಂತರಗಳಲ್ಲಿ ತೆಗೆದುಕೊಂಡ ಮೂರು ವರ್ಣಪಟಲವನ್ನು ಪ್ರಸ್ತುತಪಡಿಸುತ್ತದೆ. ಪ್ರಥಮ ( X 1) ಮತ್ತು ಎರಡನೇ ( X 2) ಎ ಮತ್ತು ಬಿ ಎರಡು ಪದಾರ್ಥಗಳ ಸಾಂದ್ರತೆಗಳು ತಿಳಿದಿರುವ ಪ್ರಮಾಣಿತ ಮಾದರಿಗಳಿಗೆ ಸ್ಪೆಕ್ಟ್ರಾವನ್ನು ಪಡೆಯಲಾಗಿದೆ: ಮೊದಲ ಮಾದರಿಯಲ್ಲಿ [ಎ] = 0.5, [ಬಿ] = 0.1, ಮತ್ತು ಎರಡನೇ ಮಾದರಿಯಲ್ಲಿ [ಎ] = 0.2, [ ಬಿ] = 0.6. ಹೊಸ, ಅಜ್ಞಾತ ಮಾದರಿಯ ಬಗ್ಗೆ ಏನು ಹೇಳಬಹುದು, ಅದರ ಸ್ಪೆಕ್ಟ್ರಮ್ ಅನ್ನು ಸೂಚಿಸಲಾಗುತ್ತದೆ X 3 ?

ನಾವು ಮೂರು ಪ್ರಾಯೋಗಿಕ ವರ್ಣಪಟಲವನ್ನು ಪರಿಗಣಿಸೋಣ X 1 , X 2 ಮತ್ತು X 3 ಆಯಾಮದ ಮೂರು ವೆಕ್ಟರ್‌ಗಳಾಗಿ 200. ರೇಖೀಯ ಬೀಜಗಣಿತವನ್ನು ಬಳಸಿ, ಒಬ್ಬರು ಅದನ್ನು ಸುಲಭವಾಗಿ ತೋರಿಸಬಹುದು X 3 = 0.1 X 1 +0.3 X 2, ಆದ್ದರಿಂದ ಮೂರನೇ ಮಾದರಿಯು ನಿಸ್ಸಂಶಯವಾಗಿ A ಮತ್ತು B ಅನ್ನು ಸಾಂದ್ರತೆಗಳಲ್ಲಿ [A] = 0.5×0.1 + 0.2×0.3 = 0.11 ಮತ್ತು [B] = 0.1×0.1 + 0.6×0.3 = 0.19 ರಲ್ಲಿ ಒಳಗೊಂಡಿರುತ್ತದೆ.

1. ಮೂಲ ಮಾಹಿತಿ

1.1 ಮ್ಯಾಟ್ರಿಕ್ಸ್

ಮ್ಯಾಟ್ರಿಕ್ಸ್ಸಂಖ್ಯೆಗಳ ಆಯತಾಕಾರದ ಕೋಷ್ಟಕ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಉದಾಹರಣೆಗೆ

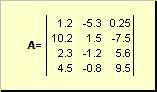
ಅಕ್ಕಿ. 2 ಮ್ಯಾಟ್ರಿಕ್ಸ್

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ದೊಡ್ಡ ದೊಡ್ಡ ಅಕ್ಷರಗಳಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ ( ಎ), ಮತ್ತು ಅವುಗಳ ಅಂಶಗಳು - ಸೂಚ್ಯಂಕಗಳೊಂದಿಗೆ ಅನುಗುಣವಾದ ಸಣ್ಣ ಅಕ್ಷರಗಳ ಮೂಲಕ, ಅಂದರೆ. ಎ ij ಮೊದಲ ಸೂಚ್ಯಂಕವು ಸಾಲುಗಳನ್ನು ಸಂಖ್ಯೆಗಳು, ಮತ್ತು ಎರಡನೆಯದು - ಕಾಲಮ್ಗಳು. ರಸಾಯನಶಾಸ್ತ್ರದಲ್ಲಿ, ಸೂಚ್ಯಂಕದ ಗರಿಷ್ಟ ಮೌಲ್ಯವನ್ನು ಸೂಚ್ಯಂಕದಂತೆಯೇ ಅದೇ ಅಕ್ಷರದೊಂದಿಗೆ ಸೂಚಿಸಲು ರೂಢಿಯಾಗಿದೆ, ಆದರೆ ದೊಡ್ಡ ಅಕ್ಷರಗಳಲ್ಲಿ. ಆದ್ದರಿಂದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಎಂದೂ ಬರೆಯಬಹುದು ( ಎ ij , i = 1,..., I; ಜ = 1,..., ಜೆ) ಉದಾಹರಣೆಗೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ I = 4, ಜೆ= 3 ಮತ್ತು ಎ 23 = −7.5.

ಜೋಡಿ ಸಂಖ್ಯೆಗಳು Iಮತ್ತು ಜೆಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಆಯಾಮ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಎಂದು ಸೂಚಿಸಲಾಗುತ್ತದೆ I× ಜೆ. ರಸಾಯನಶಾಸ್ತ್ರದಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಉದಾಹರಣೆಯೆಂದರೆ ಪಡೆದ ರೋಹಿತದ ಒಂದು ಸೆಟ್ Iಗಾಗಿ ಮಾದರಿಗಳು ಜೆತರಂಗಾಂತರಗಳು.

1.2. ಮ್ಯಾಟ್ರಿಕ್ಸ್ನೊಂದಿಗೆ ಸರಳವಾದ ಕಾರ್ಯಾಚರಣೆಗಳು

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿರಬಹುದು ಸಂಖ್ಯೆಗಳಿಂದ ಗುಣಿಸಿ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಪ್ರತಿಯೊಂದು ಅಂಶವನ್ನು ಈ ಸಂಖ್ಯೆಯಿಂದ ಗುಣಿಸಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ -

ಅಕ್ಕಿ. 3 ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಸಂಖ್ಯೆಯಿಂದ ಗುಣಿಸುವುದು

ಒಂದೇ ಆಯಾಮದ ಎರಡು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅಂಶದಿಂದ ಅಂಶವಾಗಿರಬಹುದು ಪಟ್ಟುಮತ್ತು ಕಳೆಯಿರಿ. ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 4 ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಸೇರ್ಪಡೆ

ಸಂಖ್ಯೆ ಮತ್ತು ಸೇರ್ಪಡೆಯಿಂದ ಗುಣಾಕಾರದ ಪರಿಣಾಮವಾಗಿ, ಅದೇ ಆಯಾಮದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ.

ಶೂನ್ಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಸೊನ್ನೆಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಒಂದು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ. ಇದನ್ನು ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ ಓ. ಎಂಬುದು ಸ್ಪಷ್ಟ ಎ+ಓ = ಎ, ಎ−ಎ = ಓಮತ್ತು 0 ಎ = ಓ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿರಬಹುದು ಸ್ಥಳಾಂತರ. ಈ ಕಾರ್ಯಾಚರಣೆಯ ಸಮಯದಲ್ಲಿ, ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ತಿರುಗಿಸಲಾಗುತ್ತದೆ, ಅಂದರೆ. ಸಾಲುಗಳು ಮತ್ತು ಕಾಲಮ್‌ಗಳನ್ನು ಬದಲಾಯಿಸಲಾಗಿದೆ. ಸ್ಥಾನಾಂತರವನ್ನು ಅವಿಭಾಜ್ಯದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ, ಎ"ಅಥವಾ ಸೂಚ್ಯಂಕ ಎಟಿ. ಹೀಗಾಗಿ, ವೇಳೆ ಎ = {ಎ ij , i = 1,..., I; ಜ = 1,...,ಜೆ), ಅದು ಎ t = ( ಎ ಜಿ , ಜ = 1,...,ಜೆ; ನಾನು = 1,..., I) ಉದಾಹರಣೆಗೆ

ಅಕ್ಕಿ. 5 ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವರ್ಗಾವಣೆ

ಇದು ಸ್ಪಷ್ಟವಾಗಿದೆ ( ಎ t) t = ಎ, (ಎ+ಬಿ)ಟಿ = ಎ t+ ಬಿಟಿ.

1.3. ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಗುಣಾಕಾರ

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿರಬಹುದು ಗುಣಿಸಿ, ಆದರೆ ಅವರು ಸೂಕ್ತವಾದ ಆಯಾಮಗಳನ್ನು ಹೊಂದಿದ್ದರೆ ಮಾತ್ರ. ಇದು ಏಕೆ ಎಂದು ವ್ಯಾಖ್ಯಾನದಿಂದ ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ. ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಉತ್ಪನ್ನ ಎ, ಆಯಾಮ I× ಕೆ, ಮತ್ತು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಬಿ, ಆಯಾಮ ಕೆ× ಜೆ, ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಸಿ, ಆಯಾಮ I× ಜೆ, ಅವರ ಅಂಶಗಳು ಸಂಖ್ಯೆಗಳಾಗಿವೆ

ಹೀಗಾಗಿ ಉತ್ಪನ್ನಕ್ಕಾಗಿ ಎಬಿಎಡ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನಲ್ಲಿ ಕಾಲಮ್‌ಗಳ ಸಂಖ್ಯೆ ಅಗತ್ಯ ಎಬಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನಲ್ಲಿರುವ ಸಾಲುಗಳ ಸಂಖ್ಯೆಗೆ ಸಮನಾಗಿತ್ತು ಬಿ. ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಉತ್ಪನ್ನದ ಉದಾಹರಣೆ -

Fig.6 ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಉತ್ಪನ್ನ

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಗುಣಾಕಾರದ ನಿಯಮವನ್ನು ಈ ಕೆಳಗಿನಂತೆ ರೂಪಿಸಬಹುದು. ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅಂಶವನ್ನು ಕಂಡುಹಿಡಿಯಲು ಸಿ, ಛೇದಕದಲ್ಲಿ ನಿಂತಿದೆ i-ನೇ ಸಾಲು ಮತ್ತು ಜನೇ ಕಾಲಮ್ ( ಸಿ ij) ಅಂಶದಿಂದ ಅಂಶವನ್ನು ಗುಣಿಸಬೇಕು i- ಮೊದಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಸಾಲು ಎಮೇಲೆ ಜಎರಡನೇ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಕಾಲಮ್ ಬಿಮತ್ತು ಎಲ್ಲಾ ಫಲಿತಾಂಶಗಳನ್ನು ಸೇರಿಸಿ. ಆದ್ದರಿಂದ ತೋರಿಸಿರುವ ಉದಾಹರಣೆಯಲ್ಲಿ, ಮೂರನೇ ಸಾಲು ಮತ್ತು ಎರಡನೇ ಕಾಲಮ್‌ನಿಂದ ಒಂದು ಅಂಶವನ್ನು ಮೂರನೇ ಸಾಲಿನ ಅಂಶ-ವಾರು ಉತ್ಪನ್ನಗಳ ಮೊತ್ತವಾಗಿ ಪಡೆಯಲಾಗುತ್ತದೆ ಎಮತ್ತು ಎರಡನೇ ಕಾಲಮ್ ಬಿ

Fig.7 ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಉತ್ಪನ್ನದ ಅಂಶ

ಮ್ಯಾಟ್ರಿಸಸ್ನ ಉತ್ಪನ್ನವು ಕ್ರಮವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ, ಅಂದರೆ. ಎಬಿ ≠ ಬಿ.ಎ., ಕನಿಷ್ಠ ಆಯಾಮದ ಕಾರಣಗಳಿಗಾಗಿ. ಇದು ನಾನ್-ಕಮ್ಯುಟೇಟಿವ್ ಎಂದು ಅವರು ಹೇಳುತ್ತಾರೆ. ಆದಾಗ್ಯೂ, ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಳ ಉತ್ಪನ್ನವು ಸಹಾಯಕವಾಗಿದೆ. ಎಂದು ಅರ್ಥ ಎಬಿಸಿ = (ಎಬಿ)ಸಿ = ಎ(ಬಿ.ಸಿ.) ಜೊತೆಗೆ, ಇದು ಸಹ ವಿತರಣಾ, ಅಂದರೆ. ಎ(ಬಿ+ಸಿ) = ಎಬಿ+ಎ.ಸಿ.. ಎಂಬುದು ಸ್ಪಷ್ಟ ಎ.ಓ. = ಓ.

1.4 ಸ್ಕ್ವೇರ್ ಮ್ಯಾಟ್ರಿಸಸ್

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಕಾಲಮ್‌ಗಳ ಸಂಖ್ಯೆಯು ಅದರ ಸಾಲುಗಳ ಸಂಖ್ಯೆಗೆ ಸಮನಾಗಿದ್ದರೆ ( I = ಜೆ=ಎನ್), ನಂತರ ಅಂತಹ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಚದರ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಈ ವಿಭಾಗದಲ್ಲಿ ನಾವು ಅಂತಹ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಮಾತ್ರ ಪರಿಗಣಿಸುತ್ತೇವೆ. ಈ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಳಲ್ಲಿ, ವಿಶೇಷ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿರುವ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಳನ್ನು ಪ್ರತ್ಯೇಕಿಸಬಹುದು.

ಏಕಮ್ಯಾಟ್ರಿಕ್ಸ್ (ಸೂಚಿಸಲಾಗಿದೆ ನಾನು,ಮತ್ತು ಕೆಲವೊಮ್ಮೆ ಇ) ಒಂದು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದ್ದು, ಇದರಲ್ಲಿ ಎಲ್ಲಾ ಅಂಶಗಳು ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ, ಕರ್ಣೀಯ ಪದಗಳಿಗಿಂತ ಹೊರತುಪಡಿಸಿ, 1 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ.

ನಿಸ್ಸಂಶಯವಾಗಿ ಎ.ಐ. = ಐ.ಎ. = ಎ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಕರ್ಣೀಯ, ಕರ್ಣೀಯ ಅಂಶಗಳನ್ನು ಹೊರತುಪಡಿಸಿ ಅದರ ಎಲ್ಲಾ ಅಂಶಗಳು ( ಎ ii) ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಉದಾಹರಣೆಗೆ

ಅಕ್ಕಿ. 8 ಕರ್ಣೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಮೇಲ್ಭಾಗ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ತ್ರಿಕೋನಾಕಾರದಕರ್ಣೀಯದ ಕೆಳಗೆ ಇರುವ ಎಲ್ಲಾ ಅಂಶಗಳು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿದ್ದರೆ, ಅಂದರೆ. ಎ ij= 0, ನಲ್ಲಿ i>ಜ. ಉದಾಹರಣೆಗೆ

ಅಕ್ಕಿ. 9 ಮೇಲಿನ ತ್ರಿಕೋನ ಮ್ಯಾಟ್ರಿಕ್ಸ್

ಕೆಳಗಿನ ತ್ರಿಕೋನ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಇದೇ ರೀತಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಎಂದು ಕರೆದರು ಸಮ್ಮಿತೀಯ, ವೇಳೆ ಎ t = ಎ. ಬೇರೆ ಪದಗಳಲ್ಲಿ ಎ ij = ಎ ಜಿ. ಉದಾಹರಣೆಗೆ

ಅಕ್ಕಿ. 10 ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಎಂದು ಕರೆದರು ಆರ್ಥೋಗೋನಲ್, ವೇಳೆ

ಎಟಿ ಎ = ಎ.ಎ. t = I.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಸಾಮಾನ್ಯಒಂದು ವೇಳೆ

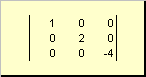
1.5 ಟ್ರೇಸ್ ಮತ್ತು ಡಿಟರ್ಮಿನೆಂಟ್

ಮುಂದೆಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ(Tr ನಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ ಎ) ಅಥವಾ ಎಸ್ಪಿ( ಎ)) ಅದರ ಕರ್ಣೀಯ ಅಂಶಗಳ ಮೊತ್ತವಾಗಿದೆ,

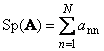
ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 11 ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಟ್ರೇಸ್

ಎಂಬುದು ಸ್ಪಷ್ಟ

Sp(α ಎ) = α Sp( ಎ) ಮತ್ತು

ಎಸ್ಪಿ( ಎ+ಬಿ) = Sp( ಎ)+ ಎಸ್ಪಿ( ಬಿ).

ಎಂದು ತೋರಿಸಬಹುದು

ಎಸ್ಪಿ( ಎ) = Sp( ಎಟಿ), ಎಸ್ಪಿ( I) = ಎನ್,

ಮತ್ತು ಅದು ಕೂಡ

ಎಸ್ಪಿ( ಎಬಿ) = Sp( ಬಿ.ಎ.).

ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಮತ್ತೊಂದು ಪ್ರಮುಖ ಲಕ್ಷಣವೆಂದರೆ ಅದು ನಿರ್ಣಾಯಕ(ಸೂಚಿಸಲಾಗಿದೆ) ಎ)) ಸಾಮಾನ್ಯ ಸಂದರ್ಭದಲ್ಲಿ ನಿರ್ಣಾಯಕವನ್ನು ನಿರ್ಧರಿಸುವುದು ತುಂಬಾ ಕಷ್ಟ, ಆದ್ದರಿಂದ ನಾವು ಸರಳವಾದ ಆಯ್ಕೆಯೊಂದಿಗೆ ಪ್ರಾರಂಭಿಸುತ್ತೇವೆ - ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಆಯಾಮ (2×2). ನಂತರ

(3×3) ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗೆ ನಿರ್ಣಾಯಕವು ಸಮನಾಗಿರುತ್ತದೆ

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಸಂದರ್ಭದಲ್ಲಿ ( ಎನ್× ಎನ್) ನಿರ್ಣಾಯಕವನ್ನು ಮೊತ್ತ 1·2·3· ... · ಎಂದು ಲೆಕ್ಕ ಹಾಕಲಾಗುತ್ತದೆ ಎನ್= ಎನ್! ನಿಯಮಗಳು, ಪ್ರತಿಯೊಂದೂ ಸಮಾನವಾಗಿರುತ್ತದೆ

ಸೂಚ್ಯಂಕಗಳು ಕೆ 1 , ಕೆ 2 ,..., ಕೆ ಎನ್ಎಲ್ಲಾ ಸಂಭವನೀಯ ಕ್ರಮಪಲ್ಲಟನೆಗಳು ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಆರ್ಸೆಟ್‌ನಲ್ಲಿರುವ ಸಂಖ್ಯೆಗಳು (1, 2, ..., ಎನ್) ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ನಿರ್ಣಾಯಕವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವುದು ಒಂದು ಸಂಕೀರ್ಣ ಕಾರ್ಯವಿಧಾನವಾಗಿದೆ, ಇದನ್ನು ಆಚರಣೆಯಲ್ಲಿ ವಿಶೇಷ ಕಾರ್ಯಕ್ರಮಗಳನ್ನು ಬಳಸಿ ನಡೆಸಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 12 ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಡಿಟರ್ಮಿನೆಂಟ್

ನಾವು ಸ್ಪಷ್ಟ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಮಾತ್ರ ಗಮನಿಸೋಣ:

det( I) = 1, det( ಎ) = det( ಎಟಿ),

det( ಎಬಿ) = det( ಎ)det ( ಬಿ).

1.6. ವಾಹಕಗಳು

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಕೇವಲ ಒಂದು ಕಾಲಮ್ ಅನ್ನು ಹೊಂದಿದ್ದರೆ ( ಜೆ= 1), ನಂತರ ಅಂತಹ ವಸ್ತುವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ವೆಕ್ಟರ್. ಹೆಚ್ಚು ನಿಖರವಾಗಿ, ಕಾಲಮ್ ವೆಕ್ಟರ್. ಉದಾಹರಣೆಗೆ

ಉದಾಹರಣೆಗೆ, ಒಂದು ಸಾಲನ್ನು ಒಳಗೊಂಡಿರುವ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಸಹ ಪರಿಗಣಿಸಬಹುದು

ಈ ವಸ್ತುವು ಸಹ ವೆಕ್ಟರ್ ಆಗಿದೆ, ಆದರೆ ಸಾಲು ವೆಕ್ಟರ್. ಡೇಟಾವನ್ನು ವಿಶ್ಲೇಷಿಸುವಾಗ, ನಾವು ಯಾವ ವೆಕ್ಟರ್ಗಳೊಂದಿಗೆ ವ್ಯವಹರಿಸುತ್ತಿದ್ದೇವೆ ಎಂಬುದನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು ಮುಖ್ಯವಾಗಿದೆ - ಕಾಲಮ್ಗಳು ಅಥವಾ ಸಾಲುಗಳು. ಆದ್ದರಿಂದ ಒಂದು ಮಾದರಿಗೆ ತೆಗೆದುಕೊಂಡ ಸ್ಪೆಕ್ಟ್ರಮ್ ಅನ್ನು ಸಾಲು ವೆಕ್ಟರ್ ಎಂದು ಪರಿಗಣಿಸಬಹುದು. ನಂತರ ಎಲ್ಲಾ ಮಾದರಿಗಳಿಗೆ ನಿರ್ದಿಷ್ಟ ತರಂಗಾಂತರದಲ್ಲಿ ರೋಹಿತದ ತೀವ್ರತೆಯ ಸೆಟ್ ಅನ್ನು ಕಾಲಮ್ ವೆಕ್ಟರ್ ಎಂದು ಪರಿಗಣಿಸಬೇಕು.

ವೆಕ್ಟರ್ನ ಆಯಾಮವು ಅದರ ಅಂಶಗಳ ಸಂಖ್ಯೆಯಾಗಿದೆ.

ಯಾವುದೇ ಕಾಲಮ್ ವೆಕ್ಟರ್ ಅನ್ನು ವರ್ಗಾವಣೆಯ ಮೂಲಕ ಸಾಲು ವೆಕ್ಟರ್ ಆಗಿ ಪರಿವರ್ತಿಸಬಹುದು ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ, ಅಂದರೆ.

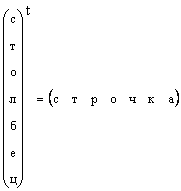
ವೆಕ್ಟರ್ನ ಆಕಾರವನ್ನು ನಿರ್ದಿಷ್ಟವಾಗಿ ನಿರ್ದಿಷ್ಟಪಡಿಸದ ಸಂದರ್ಭಗಳಲ್ಲಿ, ಆದರೆ ಸರಳವಾಗಿ ವೆಕ್ಟರ್ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ, ಆಗ ಅವುಗಳು ಕಾಲಮ್ ವೆಕ್ಟರ್ ಅನ್ನು ಅರ್ಥೈಸುತ್ತವೆ. ನಾವು ಕೂಡ ಈ ನಿಯಮವನ್ನು ಪಾಲಿಸುತ್ತೇವೆ. ವೆಕ್ಟರ್ ಅನ್ನು ಲೋವರ್ಕೇಸ್, ನೇರವಾಗಿ, ದಪ್ಪ ಅಕ್ಷರದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ. ಶೂನ್ಯ ವೆಕ್ಟರ್ ಒಂದು ವೆಕ್ಟರ್ ಆಗಿದ್ದು, ಅದರ ಎಲ್ಲಾ ಅಂಶಗಳು ಶೂನ್ಯವಾಗಿರುತ್ತದೆ. ಇದನ್ನು ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ 0 .

1.7. ವೆಕ್ಟರ್ಗಳೊಂದಿಗೆ ಸರಳವಾದ ಕಾರ್ಯಾಚರಣೆಗಳು

ವೆಕ್ಟರ್‌ಗಳನ್ನು ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಳ ರೀತಿಯಲ್ಲಿಯೇ ಸಂಖ್ಯೆಗಳಿಂದ ಕೂಡಿಸಬಹುದು ಮತ್ತು ಗುಣಿಸಬಹುದು. ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 13 ವೆಕ್ಟರ್‌ಗಳೊಂದಿಗೆ ಕಾರ್ಯಾಚರಣೆಗಳು

ಎರಡು ವಾಹಕಗಳು Xಮತ್ತು ವೈಎಂದು ಕರೆಯುತ್ತಾರೆ ಕೋಲಿನಾರ್, ಅಂತಹ ಸಂಖ್ಯೆ α ಇದ್ದರೆ

1.8 ವಾಹಕಗಳ ಉತ್ಪನ್ನಗಳು

ಒಂದೇ ಆಯಾಮದ ಎರಡು ವಾಹಕಗಳು ಎನ್ಗುಣಿಸಬಹುದು. ಎರಡು ವಾಹಕಗಳು ಇರಲಿ X = (X 1 , X 2 ,...,Xಎನ್) ಟಿ ಮತ್ತು ವೈ = (ವೈ 1 , ವೈ 2 ,...,ವೈಎನ್) ಟಿ. ಸಾಲು-ಮೂಲಕ-ಕಾಲಮ್ ಗುಣಾಕಾರ ನಿಯಮದಿಂದ ಮಾರ್ಗದರ್ಶಿಸಲ್ಪಟ್ಟ ನಾವು ಅವುಗಳಿಂದ ಎರಡು ಉತ್ಪನ್ನಗಳನ್ನು ರಚಿಸಬಹುದು: Xಟಿ ವೈಮತ್ತು xyಟಿ. ಮೊದಲ ಕೆಲಸ

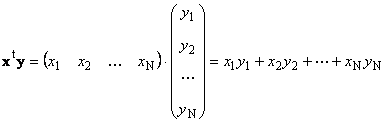
ಎಂದು ಕರೆದರು ಸ್ಕೇಲಾರ್ಅಥವಾ ಆಂತರಿಕ. ಅದರ ಫಲಿತಾಂಶವು ಒಂದು ಸಂಖ್ಯೆಯಾಗಿದೆ. ಇದನ್ನು ಸಹ ಸೂಚಿಸಲಾಗಿದೆ ( X,ವೈ)= Xಟಿ ವೈ. ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 14 ಒಳ (ಸ್ಕೇಲಾರ್) ಉತ್ಪನ್ನ

ಎರಡನೇ ತುಣುಕು

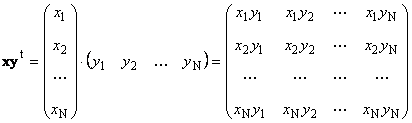
ಎಂದು ಕರೆದರು ಬಾಹ್ಯ. ಇದರ ಫಲಿತಾಂಶವು ಆಯಾಮದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ ( ಎನ್× ಎನ್) ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 15 ಬಾಹ್ಯ ಕೆಲಸ

ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನ ಶೂನ್ಯವಾಗಿರುವ ವಾಹಕಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಆರ್ಥೋಗೋನಲ್.

1.9 ವೆಕ್ಟರ್ ರೂಢಿ

ವೆಕ್ಟರ್‌ನ ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನವನ್ನು ಸ್ಕೇಲಾರ್ ಸ್ಕ್ವೇರ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಈ ಮೌಲ್ಯ

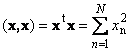
ಚೌಕವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುತ್ತದೆ ಉದ್ದವೆಕ್ಟರ್ X. ಉದ್ದವನ್ನು ಸೂಚಿಸಲು (ಇದನ್ನು ಸಹ ಕರೆಯಲಾಗುತ್ತದೆ ರೂಢಿವೆಕ್ಟರ್) ಸಂಕೇತವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ

ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 16 ವೆಕ್ಟರ್ ರೂಢಿ

ಘಟಕ ಉದ್ದ ವೆಕ್ಟರ್ (|| X|| = 1) ಅನ್ನು ಸಾಮಾನ್ಯೀಕರಿಸಲಾಗಿದೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಶೂನ್ಯವಲ್ಲದ ವೆಕ್ಟರ್ ( X ≠ 0 ) ಉದ್ದದಿಂದ ಭಾಗಿಸುವ ಮೂಲಕ ಸಾಮಾನ್ಯಗೊಳಿಸಬಹುದು, ಅಂದರೆ. X = ||X|| (X/||X||) = ||X|| ಇ. ಇಲ್ಲಿ ಇ = X/||X|| - ಸಾಮಾನ್ಯೀಕರಿಸಿದ ವೆಕ್ಟರ್.

ವಾಹಕಗಳನ್ನು ಆರ್ಥೋನಾರ್ಮಲ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಅವೆಲ್ಲವೂ ಸಾಮಾನ್ಯ ಮತ್ತು ಜೋಡಿಯಾಗಿ ಆರ್ಥೋಗೋನಲ್ ಆಗಿದ್ದರೆ.

1.10. ವಾಹಕಗಳ ನಡುವಿನ ಕೋನ

ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನವು ನಿರ್ಧರಿಸುತ್ತದೆ ಮತ್ತು ಮೂಲೆಯಲ್ಲಿಎರಡು ವಾಹಕಗಳ ನಡುವೆ φ Xಮತ್ತು ವೈ

ವಾಹಕಗಳು ಆರ್ಥೋಗೋನಲ್ ಆಗಿದ್ದರೆ, cosφ = 0 ಮತ್ತು φ = π/2, ಮತ್ತು ಅವು ಕೋಲಿನಿಯರ್ ಆಗಿದ್ದರೆ, ನಂತರ cosφ = 1 ಮತ್ತು φ = 0.

1.11. ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ವೆಕ್ಟರ್ ಪ್ರಾತಿನಿಧ್ಯ

ಪ್ರತಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಗಾತ್ರ I× ಜೆವೆಕ್ಟರ್‌ಗಳ ಗುಂಪಾಗಿ ಪ್ರತಿನಿಧಿಸಬಹುದು

ಇಲ್ಲಿ ಪ್ರತಿ ವೆಕ್ಟರ್ ಎ ಜಇದೆ ಜನೇ ಕಾಲಮ್ ಮತ್ತು ಸಾಲು ವೆಕ್ಟರ್ ಬಿ iಇದೆ iಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ನೇ ಸಾಲು ಎ

1.12. ರೇಖಾತ್ಮಕವಾಗಿ ಅವಲಂಬಿತ ವೆಕ್ಟರ್‌ಗಳು

ಒಂದೇ ಆಯಾಮದ ವಾಹಕಗಳು ( ಎನ್) ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಳಂತೆಯೇ ಸಂಖ್ಯೆಯಿಂದ ಕೂಡಿಸಬಹುದು ಮತ್ತು ಗುಣಿಸಬಹುದು. ಫಲಿತಾಂಶವು ಅದೇ ಆಯಾಮದ ವೆಕ್ಟರ್ ಆಗಿರುತ್ತದೆ. ಒಂದೇ ಆಯಾಮದ ಹಲವಾರು ವಾಹಕಗಳು ಇರಲಿ X 1 , X 2 ,...,X K ಮತ್ತು ಅದೇ ಸಂಖ್ಯೆಯ ಸಂಖ್ಯೆಗಳು α α 1 , α 2 ,...,α ಕೆ. ವೆಕ್ಟರ್

ವೈ= α 1 X 1 + α 2 X 2 +...+ α ಕೆ X ಕೆ

ಎಂದು ಕರೆದರು ರೇಖೀಯ ಸಂಯೋಜನೆವಾಹಕಗಳು X ಕೆ .

ಅಂತಹ ಶೂನ್ಯವಲ್ಲದ ಸಂಖ್ಯೆಗಳಿದ್ದರೆ α ಕೆ ≠ 0, ಕೆ = 1,..., ಕೆ, ಏನು ವೈ = 0 , ನಂತರ ಅಂತಹ ವಾಹಕಗಳ ಸೆಟ್ X ಕೆಎಂದು ಕರೆದರು ರೇಖಾತ್ಮಕವಾಗಿ ಅವಲಂಬಿತವಾಗಿದೆ. ಇಲ್ಲದಿದ್ದರೆ, ವಾಹಕಗಳು ರೇಖಾತ್ಮಕವಾಗಿ ಸ್ವತಂತ್ರವಾಗಿರುತ್ತವೆ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ವಾಹಕಗಳು X 1 = (2, 2) ಟಿ ಮತ್ತು X 2 = (-1, -1) t ರೇಖಾತ್ಮಕವಾಗಿ ಅವಲಂಬಿತವಾಗಿದೆ, ಏಕೆಂದರೆ X 1 +2X 2 = 0

1.13. ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಶ್ರೇಣಿ

ಒಂದು ಸೆಟ್ ಅನ್ನು ಪರಿಗಣಿಸಿ ಕೆವಾಹಕಗಳು X 1 , X 2 ,...,X ಕೆಆಯಾಮಗಳು ಎನ್. ವಾಹಕಗಳ ಈ ವ್ಯವಸ್ಥೆಯ ಶ್ರೇಣಿಯು ರೇಖೀಯ ಸ್ವತಂತ್ರ ವೆಕ್ಟರ್‌ಗಳ ಗರಿಷ್ಠ ಸಂಖ್ಯೆಯಾಗಿದೆ. ಉದಾಹರಣೆಗೆ ಸೆಟ್ನಲ್ಲಿ

ಕೇವಲ ಎರಡು ರೇಖೀಯ ಸ್ವತಂತ್ರ ವೆಕ್ಟರ್‌ಗಳಿವೆ, ಉದಾಹರಣೆಗೆ X 1 ಮತ್ತು X 2, ಆದ್ದರಿಂದ ಅದರ ಶ್ರೇಣಿ 2 ಆಗಿದೆ.

ನಿಸ್ಸಂಶಯವಾಗಿ, ಒಂದು ಸೆಟ್‌ನಲ್ಲಿ ಅವುಗಳ ಆಯಾಮಕ್ಕಿಂತ ಹೆಚ್ಚು ವೆಕ್ಟರ್‌ಗಳಿದ್ದರೆ ( ಕೆ>ಎನ್), ನಂತರ ಅವರು ಅಗತ್ಯವಾಗಿ ರೇಖೀಯವಾಗಿ ಅವಲಂಬಿತರಾಗಿದ್ದಾರೆ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಶ್ರೇಣಿ(ಶ್ರೇಣಿಯಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ) ಎ)) ಇದು ಒಳಗೊಂಡಿರುವ ವಾಹಕಗಳ ವ್ಯವಸ್ಥೆಯ ಶ್ರೇಣಿಯಾಗಿದೆ. ಯಾವುದೇ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಎರಡು ರೀತಿಯಲ್ಲಿ ಪ್ರತಿನಿಧಿಸಬಹುದಾದರೂ (ಕಾಲಮ್ ಅಥವಾ ಸಾಲು ವೆಕ್ಟರ್), ಇದು ಶ್ರೇಣಿಯ ಮೌಲ್ಯದ ಮೇಲೆ ಪರಿಣಾಮ ಬೀರುವುದಿಲ್ಲ, ಏಕೆಂದರೆ

1.14. ವಿಲೋಮ ಮ್ಯಾಟ್ರಿಕ್ಸ್

ಸ್ಕ್ವೇರ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎವಿಶಿಷ್ಟತೆಯನ್ನು ಹೊಂದಿದ್ದರೆ ಅದನ್ನು ಕ್ಷೀಣಿಸುವುದಿಲ್ಲ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಹಿಮ್ಮುಖಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ-1, ಷರತ್ತುಗಳಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ

ಎ.ಎ. −1 = ಎ −1 ಎ = I.

ಎಲ್ಲಾ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಳಿಗೆ ವಿಲೋಮ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲ. ಅವನತಿಯಾಗದಿರುವಿಕೆಗೆ ಅಗತ್ಯವಾದ ಮತ್ತು ಸಾಕಷ್ಟು ಸ್ಥಿತಿಯಾಗಿದೆ

det( ಎ) ≠ 0 ಅಥವಾ ಶ್ರೇಣಿ( ಎ) = ಎನ್.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವಿಲೋಮವು ಒಂದು ಸಂಕೀರ್ಣ ಕಾರ್ಯವಿಧಾನವಾಗಿದೆ, ಇದಕ್ಕಾಗಿ ವಿಶೇಷ ಕಾರ್ಯಕ್ರಮಗಳಿವೆ. ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 17 ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವಿಲೋಮ

ಸರಳವಾದ ಪ್ರಕರಣಕ್ಕೆ ಸೂತ್ರಗಳನ್ನು ಪ್ರಸ್ತುತಪಡಿಸೋಣ - 2×2 ಮ್ಯಾಟ್ರಿಕ್ಸ್

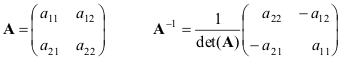
ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವೇಳೆ ಎಮತ್ತು ಬಿಕ್ಷೀಣಿಸುವುದಿಲ್ಲ, ನಂತರ

(ಎಬಿ) −1 = ಬಿ −1 ಎ −1 .

1.15. ಸ್ಯೂಡೋಇನ್ವರ್ಸ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವೇಳೆ ಎಏಕವಚನ ಮತ್ತು ವಿಲೋಮ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲ, ನಂತರ ಕೆಲವು ಸಂದರ್ಭಗಳಲ್ಲಿ ನೀವು ಬಳಸಬಹುದು ಹುಸಿ ವಿಲೋಮಮ್ಯಾಟ್ರಿಕ್ಸ್, ಅಂತಹ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಎ+ ಅದು

ಎ.ಎ. + ಎ = ಎ.

ಸ್ಯೂಡೋಇನ್ವರ್ಸ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಒಂದೇ ಅಲ್ಲ ಮತ್ತು ಅದರ ರೂಪವು ನಿರ್ಮಾಣದ ವಿಧಾನವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಆಯತಾಕಾರದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ಗಾಗಿ ನೀವು ಮೂರ್-ಪೆನ್ರೋಸ್ ವಿಧಾನವನ್ನು ಬಳಸಬಹುದು.

ಕಾಲಮ್‌ಗಳ ಸಂಖ್ಯೆಯು ಸಾಲುಗಳ ಸಂಖ್ಯೆಗಿಂತ ಕಡಿಮೆಯಿದ್ದರೆ, ಆಗ

ಎ + =(ಎಟಿ ಎ) −1 ಎಟಿ

ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 17a ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಹುಸಿ-ವಿಲೋಮ

ಕಾಲಮ್‌ಗಳ ಸಂಖ್ಯೆಯು ಸಾಲುಗಳ ಸಂಖ್ಯೆಗಿಂತ ಹೆಚ್ಚಿದ್ದರೆ, ಆಗ

ಎ + =ಎಟಿ( ಎ.ಎ.ಟಿ) −1

1.16. ಮ್ಯಾಟ್ರಿಕ್ಸ್ನಿಂದ ವೆಕ್ಟರ್ ಅನ್ನು ಗುಣಿಸುವುದು

ವೆಕ್ಟರ್ Xಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನಿಂದ ಗುಣಿಸಬಹುದು ಎಸೂಕ್ತವಾದ ಗಾತ್ರ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಕಾಲಮ್ ವೆಕ್ಟರ್ ಅನ್ನು ಬಲಭಾಗದಲ್ಲಿ ಗುಣಿಸಲಾಗುತ್ತದೆ ಕೊಡಲಿ, ಮತ್ತು ವೆಕ್ಟರ್ ಸಾಲು ಎಡಭಾಗದಲ್ಲಿದೆ Xಟಿ ಎ. ವೆಕ್ಟರ್ ಆಯಾಮವಾಗಿದ್ದರೆ ಜೆ, ಮತ್ತು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಯಾಮ I× ಜೆನಂತರ ಫಲಿತಾಂಶವು ಆಯಾಮದ ವೆಕ್ಟರ್ ಆಗಿರುತ್ತದೆ I. ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 18 ವೆಕ್ಟರ್ ಅನ್ನು ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನಿಂದ ಗುಣಿಸುವುದು

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವೇಳೆ ಎ- ಚದರ ( I× I), ನಂತರ ವೆಕ್ಟರ್ ವೈ = ಕೊಡಲಿಅದೇ ಆಯಾಮವನ್ನು ಹೊಂದಿದೆ X. ಎಂಬುದು ಸ್ಪಷ್ಟ

ಎ(α 1 X 1 + α 2 X 2) = α 1 ಕೊಡಲಿ 1 + α 2 ಕೊಡಲಿ 2 .

ಆದ್ದರಿಂದ, ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ವೆಕ್ಟರ್ಗಳ ರೇಖೀಯ ರೂಪಾಂತರಗಳಾಗಿ ಪರಿಗಣಿಸಬಹುದು. ನಿರ್ದಿಷ್ಟವಾಗಿ Ix = X, ಎತ್ತು = 0 .

2. ಹೆಚ್ಚುವರಿ ಮಾಹಿತಿ

2.1. ರೇಖೀಯ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಗಳು

ಅವಕಾಶ ಎ- ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಗಾತ್ರ I× ಜೆ, ಎ ಬಿ- ಆಯಾಮ ವೆಕ್ಟರ್ ಜೆ. ಸಮೀಕರಣವನ್ನು ಪರಿಗಣಿಸಿ

ಕೊಡಲಿ = ಬಿ

ವೆಕ್ಟರ್ಗೆ ಸಂಬಂಧಿಸಿದಂತೆ X, ಆಯಾಮಗಳು I. ಮೂಲಭೂತವಾಗಿ, ಇದು ಒಂದು ವ್ಯವಸ್ಥೆಯಾಗಿದೆ Iಜೊತೆ ರೇಖೀಯ ಸಮೀಕರಣಗಳು ಜೆಅಜ್ಞಾತ X 1 ,...,X ಜೆ. ಒಂದು ವೇಳೆ ಮತ್ತು ಇದ್ದರೆ ಮಾತ್ರ ಪರಿಹಾರ ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ

ಶ್ರೇಣಿ ( ಎ) = ಶ್ರೇಣಿ ( ಬಿ) = ಆರ್,

ಎಲ್ಲಿ ಬಿಆಯಾಮಗಳ ವಿಸ್ತೃತ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ I×( J+1), ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ ಎ, ಕಾಲಮ್‌ನಿಂದ ಪೂರಕವಾಗಿದೆ ಬಿ, ಬಿ = (ಎ ಬಿ) ಇಲ್ಲದಿದ್ದರೆ, ಸಮೀಕರಣಗಳು ಅಸಮಂಜಸವಾಗಿರುತ್ತವೆ.

ಒಂದು ವೇಳೆ ಆರ್ = I = ಜೆ, ನಂತರ ಪರಿಹಾರ ಅನನ್ಯವಾಗಿದೆ

X = ಎ −1 ಬಿ.

ಒಂದು ವೇಳೆ ಆರ್ < I, ನಂತರ ರೇಖೀಯ ಸಂಯೋಜನೆಯ ಮೂಲಕ ವ್ಯಕ್ತಪಡಿಸಬಹುದಾದ ಹಲವು ವಿಭಿನ್ನ ಪರಿಹಾರಗಳಿವೆ ಜೆ−ಆರ್ವಾಹಕಗಳು. ಏಕರೂಪದ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆ ಕೊಡಲಿ = 0 ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ನೊಂದಿಗೆ ಎ (ಎನ್× ಎನ್ಕ್ಷುಲ್ಲಕವಲ್ಲದ ಪರಿಹಾರವನ್ನು ಹೊಂದಿದೆ ( X ≠ 0 ) ಇದ್ದರೆ ಮತ್ತು ಅದು ಮಾತ್ರ ( ಎ) = 0. ವೇಳೆ ಆರ್= ಶ್ರೇಣಿ ( ಎ)<ಎನ್, ನಂತರ ಇವೆ ಎನ್−ಆರ್ರೇಖೀಯ ಸ್ವತಂತ್ರ ಪರಿಹಾರಗಳು.

2.2 ಬೈಲಿನಿಯರ್ ಮತ್ತು ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪಗಳು

ಒಂದು ವೇಳೆ ಎಒಂದು ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್, ಮತ್ತು Xಮತ್ತು ವೈ- ಅನುಗುಣವಾದ ಆಯಾಮದ ವೆಕ್ಟರ್, ನಂತರ ರೂಪದ ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನ Xಟಿ ಆಯ್ಎಂದು ಕರೆದರು ಬೈಲಿನಿಯರ್ರೂಪವನ್ನು ಮ್ಯಾಟ್ರಿಕ್ಸ್ನಿಂದ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಎ. ನಲ್ಲಿ X = ವೈಅಭಿವ್ಯಕ್ತಿ Xಟಿ ಕೊಡಲಿಎಂದು ಕರೆದರು ಚತುರ್ಭುಜರೂಪ.

2.3 ಧನಾತ್ಮಕ ನಿರ್ದಿಷ್ಟ ಮ್ಯಾಟ್ರಿಕ್ಸ್

ಸ್ಕ್ವೇರ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಎಂದು ಕರೆದರು ಧನಾತ್ಮಕ ಖಚಿತ, ಯಾವುದೇ ಶೂನ್ಯವಲ್ಲದ ವೆಕ್ಟರ್‌ಗಾಗಿ X ≠ 0 ,

Xಟಿ ಕೊಡಲಿ > 0.

ಅಂತೆಯೇ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಋಣಾತ್ಮಕ (Xಟಿ ಕೊಡಲಿ < 0), ಋಣಾತ್ಮಕವಲ್ಲದ (Xಟಿ ಕೊಡಲಿ≥ 0) ಮತ್ತು ಋಣಾತ್ಮಕ (Xಟಿ ಕೊಡಲಿ≤ 0) ಕೆಲವು ಮ್ಯಾಟ್ರಿಕ್ಸ್.

2.4 ಚೋಲೆಸ್ಕಿ ವಿಭಜನೆ

ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವೇಳೆ ಎಧನಾತ್ಮಕ ಖಚಿತವಾಗಿದೆ, ನಂತರ ಒಂದು ಅನನ್ಯ ತ್ರಿಕೋನ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಇರುತ್ತದೆ ಯುಧನಾತ್ಮಕ ಅಂಶಗಳೊಂದಿಗೆ, ಇದಕ್ಕಾಗಿ

ಎ = ಯುಟಿ ಯು.

ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 19 ಚೋಲೆಸ್ಕಿ ವಿಭಜನೆ

2.5 ಧ್ರುವ ವಿಘಟನೆ

ಅವಕಾಶ ಎಆಯಾಮದ ಏಕವಚನವಲ್ಲದ ಚೌಕದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ ಎನ್× ಎನ್. ನಂತರ ಒಂದು ವಿಶಿಷ್ಟವಿದೆ ಧ್ರುವೀಯಪ್ರದರ್ಶನ

ಎ = ಎಸ್.ಆರ್.

ಎಲ್ಲಿ ಎಸ್ಋಣಾತ್ಮಕವಲ್ಲದ ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್, ಮತ್ತು ಆರ್ಆರ್ಥೋಗೋನಲ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ. ಮ್ಯಾಟ್ರಿಸಸ್ ಎಸ್ಮತ್ತು ಆರ್ಸ್ಪಷ್ಟವಾಗಿ ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು:

ಎಸ್ 2 = ಎ.ಎ.ಟಿ ಅಥವಾ ಎಸ್ = (ಎ.ಎ. t) ½ ಮತ್ತು ಆರ್ = ಎಸ್ −1 ಎ = (ಎ.ಎ. t) -½ ಎ.

ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 20 ಧ್ರುವ ವಿಘಟನೆ

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವೇಳೆ ಎಕ್ಷೀಣಿಸುತ್ತದೆ, ನಂತರ ವಿಭಜನೆಯು ಅನನ್ಯವಾಗಿಲ್ಲ - ಅವುಗಳೆಂದರೆ: ಎಸ್ಇನ್ನೂ ಒಂಟಿ, ಆದರೆ ಆರ್ಬಹುಶಃ ಬಹಳಷ್ಟು. ಧ್ರುವ ವಿಭಜನೆಯು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ ಎಸಂಕೋಚನ/ವಿಸ್ತರಣೆಯ ಸಂಯೋಜನೆಯಾಗಿ ಎಸ್ಮತ್ತು ತಿರುಗಿ ಆರ್.

2.6. ಈಜೆನ್ವೆಕ್ಟರ್‌ಗಳು ಮತ್ತು ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು

ಅವಕಾಶ ಎಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ. ವೆಕ್ಟರ್ vಎಂದು ಕರೆದರು ಐಜೆನ್ವೆಕ್ಟರ್ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ, ವೇಳೆ

Av = λ v,

ಅಲ್ಲಿ λ ಸಂಖ್ಯೆಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಸಮಾನ ಮೌಲ್ಯಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ. ಹೀಗಾಗಿ, ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನಿರ್ವಹಿಸುವ ರೂಪಾಂತರ ಎವೆಕ್ಟರ್ ಮೇಲೆ v, ಗುಣಾಂಕ λ ನೊಂದಿಗೆ ಸರಳ ವಿಸ್ತರಣೆ ಅಥವಾ ಸಂಕೋಚನಕ್ಕೆ ಬರುತ್ತದೆ. ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಸ್ಥಿರ α ≠ 0 ರಿಂದ ಗುಣಾಕಾರದವರೆಗೆ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ, ಅಂದರೆ. ಒಂದು ವೇಳೆ vಐಜೆನ್ವೆಕ್ಟರ್ ಆಗಿದ್ದು, ನಂತರ α v- ಐಜೆನ್ವೆಕ್ಟರ್ ಕೂಡ.

2.7. ಐಜೆನ್ವಾಲ್ಯೂಸ್

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನಲ್ಲಿ ಎ, ಆಯಾಮ ( ಎನ್× ಎನ್) ಗಿಂತ ಹೆಚ್ಚಿರಬಾರದು ಎನ್ಸಮಾನ ಮೌಲ್ಯಗಳು. ಅವರು ತೃಪ್ತಿಪಡಿಸುತ್ತಾರೆ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ

det( ಎ − λ I) = 0,

ಇದು ಬೀಜಗಣಿತದ ಸಮೀಕರಣವಾಗಿದೆ ಎನ್- ನೇ ಆದೇಶ. ನಿರ್ದಿಷ್ಟವಾಗಿ, 2×2 ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗೆ ವಿಶಿಷ್ಟ ಸಮೀಕರಣವು ರೂಪವನ್ನು ಹೊಂದಿರುತ್ತದೆ

ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 21 ಐಜೆನ್ ವ್ಯಾಲ್ಯೂಸ್

ಐಜೆನ್ವಾಲ್ಯೂಗಳ ಸೆಟ್ λ 1 ,..., λ ಎನ್ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಎಂದು ಕರೆದರು ಸ್ಪೆಕ್ಟ್ರಮ್ ಎ.

ಸ್ಪೆಕ್ಟ್ರಮ್ ವಿವಿಧ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿದೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ

det( ಎ) = λ 1 ×...×λ ಎನ್,ಎಸ್ಪಿ( ಎ) = λ 1 +...+λ ಎನ್.

ಅನಿಯಂತ್ರಿತ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ಸಂಕೀರ್ಣ ಸಂಖ್ಯೆಗಳಾಗಿರಬಹುದು, ಆದರೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಸಮ್ಮಿತೀಯವಾಗಿದ್ದರೆ ( ಎ t = ಎ), ನಂತರ ಅದರ ಸಮಾನ ಮೌಲ್ಯಗಳು ನಿಜ.

2.8 ಐಜೆನ್ವೆಕ್ಟರ್ಸ್

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನಲ್ಲಿ ಎ, ಆಯಾಮ ( ಎನ್× ಎನ್) ಗಿಂತ ಹೆಚ್ಚಿರಬಾರದು ಎನ್ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು, ಪ್ರತಿಯೊಂದೂ ತನ್ನದೇ ಆದ ಐಜೆನ್‌ವಾಲ್ಯೂಗೆ ಅನುರೂಪವಾಗಿದೆ. ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ನಿರ್ಧರಿಸಲು v ಎನ್ಏಕರೂಪದ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯನ್ನು ಪರಿಹರಿಸುವ ಅಗತ್ಯವಿದೆ

(ಎ − λ ಎನ್ I)v ಎನ್ = 0 .

ಇದು ಕ್ಷುಲ್ಲಕವಲ್ಲದ ಪರಿಹಾರವನ್ನು ಹೊಂದಿದೆ, ಏಕೆಂದರೆ det( ಎ -λ ಎನ್ I) = 0.

ಉದಾಹರಣೆಗೆ,

ಅಕ್ಕಿ. 22 ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು

ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು ಆರ್ಥೋಗೋನಲ್ ಆಗಿರುತ್ತವೆ.