Најдете сопствени вредности и сопствени вектори на примери на матрици. Карактеристична равенка на матрицата

СИСТЕМ НА ХОМОГЕНИ ЛИНЕАРНИ РАВЕНКИ

Систем на хомогени линеарни равенки е систем на форма

Јасно е дека во овој случај , бидејќи сите елементи на една од колоните во овие детерминанти се еднакви на нула.

Бидејќи непознатите се наоѓаат со формулите , тогаш во случај кога Δ ≠ 0, системот има единствено нула решение x = y = z= 0. Меѓутоа, во многу проблеми е од интерес прашањето дали хомоген систем има решенија различни од нула.

Теорема.За систем од линеарни хомогени равенки да има ненула решение, потребно е и доволно Δ ≠ 0.

Значи, ако детерминантата е Δ ≠ 0, тогаш системот има единствено решение. Ако Δ ≠ 0, тогаш системот на линеарни хомогени равенки има бесконечен број решенија.

Примери.

Сопствени вектори и матрични сопствени вредности

Нека е дадена квадратна матрица , Xе некоја матрица-колона чија висина се совпаѓа со редоследот на матрицата А. .

Во многу проблеми, треба да се земе предвид равенката за X

каде λ е некој број. Јасно е дека за кое било λ оваа равенка има нула решение.

Се вика бројот λ за кој оваа равенка има ненула решенија сопствена вредностматрици А, А Xза такво λ се вика сопствен векторматрици А.

Да го најдеме сопствениот вектор на матрицата А. Затоа што Е∙X=X, тогаш матричната равенка може да се препише како или . Во проширена форма, оваа равенка може да се препише како систем на линеарни равенки. Навистина .

А со тоа и

Значи, добивме систем на хомогени линеарни равенки за одредување на координатите x 1, x2, x 3вектор X. За системот да има ненулта решенија, потребно е и доволно детерминантата на системот да биде еднаква на нула, т.е.

Ова е равенка од 3 степен во однос на λ. Се вика карактеристична равенкаматрици Аи служи за одредување на сопствените вредности λ.

Секоја сопствена вредност λ одговара на сопствен вектор X, чии координати се одредуваат од системот со соодветна вредност λ.

Примери.

ВЕКТОРСКА АЛГЕБРА. КОНЦЕПТ НА ВЕКТОР

При изучување на различни гранки на физиката, постојат количини кои целосно се одредуваат со поставување на нивните нумерички вредности, на пример, должина, површина, маса, температура итн. Таквите вредности се нарекуваат скаларни. Но, покрај нив има и количини, за чиешто определување, покрај бројната вредност, потребно е да се знае и нивниот правец во просторот, на пример, силата што делува на телото, брзината и забрзувањето. на телото кога се движи во просторот, јачината на магнетното поле во дадена точка во просторот и сл. Таквите величини се нарекуваат векторски величини.

Да воведеме ригорозна дефиниција.

Насочен сегментДа наречеме отсечка, во однос на чии краеви се знае кој од нив е прв, а кој втор.

Векторсе нарекува насочен сегмент, кој има одредена должина, т.е. Ова е сегмент со одредена должина, во кој една од точките што го ограничуваат се зема како почеток, а втората - како крај. Ако Ае почеток на векторот, Бе неговиот крај, тогаш векторот се означува со симболот, покрај тоа, векторот често се означува со една буква. На сликата векторот е означен со сегмент, а неговата насока со стрелка.

модулили долговектор се нарекува должина на насочениот сегмент што го дефинира. Означено со || или ||.

Таканаречениот нулта вектор, чиј почеток и крај се совпаѓаат, исто така ќе се нарекуваат вектори. Тоа е означено. Нултиот вектор нема одредена насока и неговиот модул е еднаков на нула ||=0.

Вектори и се нарекуваат колинеарнаако се наоѓаат на иста права или на паралелни прави. Во овој случај, ако векторите и се подеднакво насочени, ќе напишеме , спротивно.

Се нарекуваат вектори лоцирани на прави паралелни на истата рамнина компланарни.

Два вектори и се нарекуваат еднаквиако се колинеарни, имаат иста насока и се еднакви по должина. Во овој случај, напишете.

Од дефиницијата за еднаквост на вектори произлегува дека векторот може да се помести паралелно со себе со поставување на неговото потекло во која било точка во просторот.

На пример.

ЛИНЕАРНИ ОПЕРАЦИИ НА ВЕКТОРИ

Множење на вектор со број.
Производот на вектор со број λ е нов вектор таков што:

Производот на вектор и број λ се означува со .

На пример,е вектор кој покажува во иста насока како векторот и има должина половина од векторот.

Внесената операција го има следново својства:
Собирање на вектори.
Нека и се два произволни вектори. Земете произволна точка Ои конструирај вектор . После тоа, од точка Атргнете го настрана векторот . Се нарекува векторот што го поврзува почетокот на првиот вектор со крајот на вториот сумаод овие вектори и се означува .

Формулираната дефиниција за векторско собирање се нарекува паралелограм правило, бидејќи истиот збир на вектори може да се добие на следниов начин. Тргнете настрана од точката Овектори и . Конструирај паралелограм на овие вектори OABC. Бидејќи векторите , тогаш векторот , кој е дијагонала на паралелограмот извлечен од темето О, очигледно ќе биде збир на вектори .

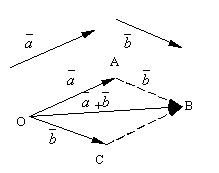
Лесно е да се провери следново својства на векторско додавање.
Разлика на вектори.
Се нарекува вектор колинеарен на даден вектор, еднаков по должина и спротивно насочен спротивновектор за вектор и се означува со . Спротивниот вектор може да се смета како резултат на векторското множење со бројот λ = –1: .

Како да вметнете математички формули на страницата?

Ако некогаш треба да додадете една или две математички формули на веб-страница, тогаш најлесниот начин да го направите ова е како што е опишано во статијата: математичките формули лесно се вметнуваат на страницата во форма на слики што Wolfram Alpha автоматски ги генерира. Покрај едноставноста, овој универзален метод ќе помогне да се подобри видливоста на страницата во пребарувачите. Работи долго време (и мислам дека ќе работи засекогаш), но морално е застарено.

Ако постојано користите математички формули на вашиот сајт, тогаш ви препорачувам да користите MathJax, специјална библиотека JavaScript која прикажува математички нотација во веб-прелистувачите користејќи ознака MathML, LaTeX или ASCIIMathML.

Постојат два начина да започнете со користење на MathJax: (1) со користење на едноставен код, можете брзо да поврзете скрипта MathJax на вашата страница, која автоматски ќе се вчита од оддалечен сервер во вистинско време (листа на сервери); (2) поставете ја скриптата MathJax од оддалечен сервер на вашиот сервер и поврзете ја на сите страници на вашата страница. Вториот метод е покомплексен и одзема многу време и ќе ви овозможи да го забрзате вчитувањето на страниците на вашата страница, а ако матичниот сервер MathJax поради некоја причина привремено стане недостапен, тоа нема да влијае на вашата веб-страница на кој било начин. И покрај овие предности, го избрав првиот метод, бидејќи е поедноставен, побрз и не бара технички вештини. Следете го мојот пример и во рок од 5 минути ќе можете да ги користите сите карактеристики на MathJax на вашата страница.

Можете да ја поврзете скриптата за библиотека MathJax од оддалечен сервер користејќи две опции за код земени од главната веб-локација на MathJax или од страницата со документација:

Една од овие опции за код треба да се копира и залепи во кодот на вашата веб-страница, по можност помеѓу ознаките иили веднаш по ознаката . Според првата опција, MathJax се вчитува побрзо и помалку ја успорува страницата. Но, втората опција автоматски ги следи и вчитува најновите верзии на MathJax. Ако го вметнете првиот код, тогаш ќе треба периодично да се ажурира. Ако го залепите вториот код, тогаш страниците ќе се вчитуваат побавно, но нема да треба постојано да ги следите ажурирањата на MathJax.

Најлесен начин за поврзување на MathJax е во Blogger или WordPress: во контролната табла на страницата, додајте графичка контрола дизајнирана за вметнување JavaScript код од трета страна, копирајте ја првата или втората верзија на кодот за вчитување погоре во неа и поставете го додатокот поблиску до почетокот на шаблонот (патем, ова воопшто не е потребно, бидејќи скриптата MathJax се вчитува асинхроно). Тоа е се. Сега научете ја синтаксата за обележување MathML, LaTeX и ASCIIMathML и подготвени сте да ги вметнете математичките формули во вашите веб-страници.

Секој фрактал е изграден според одредено правило, кое постојано се применува неограничен број пати. Секое такво време се нарекува итерација.

Итеративниот алгоритам за конструирање на сунѓер Менгер е прилично едноставен: оригиналната коцка со страна 1 е поделена со рамнини паралелни на нејзините лица на 27 еднакви коцки. Од него се отстрануваат една централна коцка и 6 коцки во непосредна близина на неа по лицата. Излегува сет кој се состои од 20 преостанати помали коцки. Правејќи го истото со секоја од овие коцки, добиваме сет составен од 400 помали коцки. Продолжувајќи го овој процес на неодредено време, го добиваме сунѓерот Менгер.

Својствектор на квадратна матрица е оној кој, кога се множи со дадена матрица, резултира со колинеарен вектор. Со едноставни зборови, кога матрицата се множи со сопствен вектор, вториот останува иста, но се множи со некој број.

Дефиниција

Сопствениот вектор е ненулта вектор V, кој, кога ќе се помножи со квадратна матрица M, станува сам по себе, зголемен за одреден број λ. Во алгебарска нотација, ова изгледа вака:

M × V = λ × V,

каде λ е сопствена вредност на матрицата M.

Да разгледаме нумерички пример. За погодност при пишувањето, броевите во матрицата ќе бидат одделени со точка-запирка. Да речеме дека имаме матрица:

М = 0; четири;
6; 10.

Ајде да го помножиме со вектор на колона:

V = -2;

Кога множиме матрица со вектор на колона, добиваме и вектор на колона. Во строг математички јазик, формулата за множење на матрица 2 × 2 со вектор на колона би изгледала вака:

M × V = M11 × V11 + M12 × V21;
M21 x V11 + M22 x V21.

M11 значи елемент од матрицата M, кој стои во првиот ред и првата колона, а M22 е елементот што се наоѓа во вториот ред и втората колона. За нашата матрица, овие елементи се M11 = 0, M12 = 4, M21 = 6, M22 10. За вектор на колона, овие вредности се V11 = –2, V21 = 1. Според оваа формула, го добиваме следново резултат на производот на квадратна матрица со вектор:

M × V = 0 × (-2) + (4) × (1) = 4;
6 × (-2) + 10 × (1) = -2.

За погодност, го запишуваме векторот на колоната во ред. Значи, ја помноживме квадратната матрица со векторот (-2; 1), што резултира со векторот (4; -2). Очигледно, ова е истиот вектор помножен со λ = -2. Ламбда во овој случај означува сопствена вредност на матрицата.

Сопствениот вектор на матрицата е колинеарен вектор, односно објект што не ја менува својата позиција во просторот кога се множи со матрица. Концептот на колинеарност во векторската алгебра е сличен на терминот паралелизам во геометријата. Во геометриската интерпретација, колинеарните вектори се паралелно насочени сегменти со различни должини. Од времето на Евклид, знаеме дека една права има бесконечен број на прави паралелни со неа, па логично е да се претпостави дека секоја матрица има бесконечен број сопствени вектори.

Од претходниот пример, може да се види дека и (-8; 4), и (16; -8), и (32, -16) можат да бидат сопствени вектори. Сите овие се колинеарни вектори што одговараат на сопствената вредност λ = -2. При множење на оригиналната матрица со овие вектори, сепак ќе добиеме вектор како резултат, кој се разликува од оригиналот за 2 пати. Затоа, при решавање на задачи за наоѓање сопствен вектор, потребно е да се најдат само линеарно независни векторски објекти. Најчесто, за n × n матрица, има n-ти број на сопствени вектори. Нашиот калкулатор е дизајниран за анализа на квадратни матрици од втор ред, така што речиси секогаш ќе се најдат два сопствени вектори како резултат, освен кога се совпаѓаат.

Во горниот пример, однапред го знаевме сопствениот вектор на оригиналната матрица и визуелно го одредивме бројот на ламбда. Меѓутоа, во пракса, сè се случува обратно: на почетокот има сопствени вредности и дури потоа сопствени вектори.

Алгоритам за решение

Ајде повторно да ја погледнеме оригиналната матрица M и да се обидеме да ги најдеме двата нејзини сопствени вектори. Значи, матрицата изгледа вака:

М = 0; четири;
6; 10.

За почеток, треба да ја одредиме сопствената вредност λ, за која треба да ја пресметаме детерминантата на следнава матрица:

(0 − λ); четири;
6; (10 − λ).

Оваа матрица се добива со одземање на непознатата λ од елементите на главната дијагонала. Детерминантата се одредува со стандардната формула:

detA = M11 × M21 − M12 × M22
detA = (0 − λ) × (10 − λ) − 24

Бидејќи нашиот вектор не смее да биде нула, ја земаме добиената равенка како линеарно зависна и ја изедначуваме нашата детерминанта detA на нула.

(0 − λ) × (10 − λ) − 24 = 0

Ајде да ги отвориме заградите и да ја добиеме карактеристичната равенка на матрицата:

λ 2 − 10λ − 24 = 0

Ова е стандардна квадратна равенка која треба да се реши во однос на дискриминаторката.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Коренот на дискриминаторот е sqrt(D) = 14, значи λ1 = -2, λ2 = 12. Сега за секоја ламбда вредност, треба да најдеме сопствен вектор. Да ги изразиме коефициентите на системот за λ = -2.

M − λ × E = 2; четири;
6; 12.

Во оваа формула, Е е матрицата на идентитетот. Врз основа на добиената матрица, составуваме систем од линеарни равенки:

2x + 4y = 6x + 12y

каде x и y се елементи на сопствениот вектор.

Ајде да ги собереме сите X лево и сите Y од десната страна. Очигледно - 4x = 8y. Поделете го изразот со - 4 и добијте x = -2y. Сега можеме да го одредиме првиот сопствен вектор на матрицата земајќи ги сите вредности на непознатите (запомнете за бесконечноста на линеарно зависните сопствени вектори). Да земеме y = 1, а потоа x = -2. Затоа, првиот сопствен вектор изгледа како V1 = (–2; 1). Врати се на почетокот на статијата. Токму со овој векторски објект ја помноживме матрицата за да го демонстрираме концептот на сопствен вектор.

Сега да го најдеме сопствениот вектор за λ = 12.

M - λ × E = -12; четири
6; -2.

Да го составиме истиот систем на линеарни равенки;

-12x + 4y = 6x − 2y
-18x = -6г
3x=y.

Сега да земеме x = 1, па оттука y = 3. Така, вториот сопствен вектор изгледа како V2 = (1; 3). При множење на оригиналната матрица со овој вектор, резултатот секогаш ќе биде истиот вектор помножен со 12. Ова го комплетира алгоритмот за решение. Сега знаете како рачно да дефинирате сопствен вектор на матрицата.

детерминанта;
трага, односно збир на елементите на главната дијагонала;
ранг, односно максимален број на линеарно независни редови/колони.

Програмата работи според горенаведениот алгоритам, минимизирајќи го процесот на решавање. Важно е да се истакне дека во програмата ламбда се означува со буквата „в“. Ајде да погледнеме нумерички пример.

Пример за програма

Ајде да се обидеме да дефинираме сопствени вектори за следната матрица:

М=5; 13;
4; 14.

Ајде да ги внесеме овие вредности во ќелиите на калкулаторот и да го добиеме одговорот во следната форма:

Ранг на матрица: 2;
Детерминанта на матрицата: 18;
Матрична трага: 19;
Пресметка на сопствени вектори: c 2 − 19.00c + 18.00 (карактеристична равенка);
Пресметка на сопствени вектори: 18 (прва ламбда вредност);
Пресметка на сопствени вектори: 1 (втора ламбда вредност);
Систем на равенки на векторот 1: -13x1 + 13y1 = 4x1 − 4y1;
Систем на равенки на вектор 2: 4x1 + 13y1 = 4x1 + 13y1;
Својствектор 1: (1; 1);
Својствектор 2: (-3,25; 1).

Така, добивме два линеарно независни сопствени вектори.

Заклучок

Линеарна алгебра и аналитичка геометрија се стандардни предмети за секој бруцош по инженерство. Голем број вектори и матрици е застрашувачки и лесно е да се направи грешка во таквите гломазни пресметки. Нашата програма ќе им овозможи на студентите да ги проверат своите пресметки или автоматски да го решат проблемот со наоѓање сопствен вектор. Во нашиот каталог има и други линеарни алгебарски калкулатори, користете ги во вашето учење или работа.

Со матрицата А, ако има број l таков што AX = lX.

Во овој случај, бројот l се нарекува сопствена вредностоператор (матрица А) што одговара на векторот X.

Со други зборови, сопствен вектор е вектор кој под дејство на линеарен оператор се трансформира во колинеарен вектор, т.е. само помножете се со некој број. Спротивно на тоа, несоодветните вектори потешко се трансформираат.

Дефиницијата на сопствениот вектор ја пишуваме како систем од равенки:

Ајде да ги преместиме сите поими на левата страна:

Последниот систем може да се напише во форма на матрица како што следува:

(A - lE)X \u003d О

Добиениот систем секогаш има нула решение X = O. Таквите системи во кои сите слободни членови се еднакви на нула се нарекуваат хомогена. Ако матрицата на таков систем е квадрат, а нејзината детерминанта не е еднаква на нула, тогаш според формулите на Крамер, секогаш ќе добиеме единствено решение - нула. Може да се докаже дека системот има ненулта решенија ако и само ако детерминантата на оваа матрица е еднаква на нула, т.е.

|A - lE| = = 0

Оваа равенка со непозната l се нарекува карактеристична равенка (карактеристичен полином) матрица А (линеарен оператор).

Може да се докаже дека карактеристичниот полином на линеарен оператор не зависи од изборот на основата.

На пример, да ги најдеме сопствените вредности и сопствени вектори на линеарниот оператор дадени со матрицата A = .

За да го направите ова, ја составуваме карактеристичната равенка |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; сопствени вредности l 1 = (2 - 12) / 2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

За да ги најдеме сопствените вектори, решаваме два системи на равенки

(A + 5E) X = O

(A - 7E) X = O

За првиот од нив, проширената матрица ќе има форма

од каде x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, т.е. X (1) \u003d (- (2/3) s; s).

За втората од нив, проширената матрица ќе има форма

од каде x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, т.е. X (2) \u003d ((2/3) s 1; s 1).

Така, сопствени вектори на овој линеарен оператор се сите вектори од формата (-(2/3)c; c) со сопствена вредност (-5) и сите вектори од формата ((2/3)c 1 ; c 1) со сопствена вредност 7 .

Може да се докаже дека матрицата на операторот А во основата што се состои од неговите сопствени вектори е дијагонална и има форма:

каде што l i се сопствените вредности на оваа матрица.

Обратно е исто така точно: ако матрицата А во некоја основа е дијагонална, тогаш сите вектори од оваа основа ќе бидат сопствени вектори на оваа матрица.

Може да се докаже и дека ако линеарен оператор има n парови различни сопствени вредности, тогаш соодветните сопствени вектори се линеарно независни, а матрицата на овој оператор во соодветната основа има дијагонална форма.

Да го објасниме ова со претходниот пример. Да земеме произволни не-нула вредности c и c 1 , но такви што векторите X (1) и X (2) се линеарно независни, т.е. би била основа. На пример, нека c \u003d c 1 \u003d 3, потоа X (1) \u003d (-2; 3), X (2) \u003d (2; 3).

Дозволете ни да ја потврдиме линеарната независност на овие вектори:

12 ≠ 0. Во оваа нова основа, матрицата A ќе има форма A * = .

За да го потврдиме ова, ја користиме формулата A * = C -1 AC. Прво да го најдеме C -1.

C -1 = ;

Квадратни форми

квадратна форма f (x 1, x 2, x n) од n променливи се нарекува збир, чиј член е или квадрат на една од променливите, или производ на две различни променливи, земени со одреден коефициент: f (x 1 , x 2, x n) = (а иј = а џи).

Се нарекува матрицата А, составена од овие коефициенти матрицаквадратна форма. Секогаш е симетричниматрица (т.е., матрица симетрична во однос на главната дијагонала, a ij = a ji).

Во матричната нотација, квадратната форма има форма f(X) = X T AX, каде

Навистина

На пример, да ја напишеме квадратната форма во форма на матрица.

За да го направите ова, наоѓаме матрица на квадратна форма. Неговите дијагонални елементи се еднакви на коефициентите на квадратите на променливите, а останатите елементи се еднакви на половина од соодветните коефициенти на квадратната форма. Затоа

Нека матрицата-колона на променливите X се добие со недегенерирана линеарна трансформација на матрицата-колона Y, т.е. X = CY, каде што C е недегенерирана матрица од редот n. Тогаш квадратната форма f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Така, при недегенерирана линеарна трансформација C, матрицата на квадратната форма добива форма: A * = C T AC.

На пример, да ја најдеме квадратната форма f(y 1, y 2) добиена од квадратната форма f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 со линеарна трансформација.

Квадратната форма се нарекува канонски(Тоа има канонски поглед) ако сите негови коефициенти a ij = 0 за i ≠ j, т.е.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Неговата матрица е дијагонална.

Теорема(доказот не е даден овде). Секоја квадратна форма може да се сведе на канонска форма користејќи недегенерирана линеарна трансформација.

На пример, да ја сведеме на канонска форма квадратната форма
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

За да го направите ова, прво изберете го целосниот квадрат за променливата x 1:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3.

Сега го избираме целосниот квадрат за променливата x 2:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Потоа, недегенерираната линеарна трансформација y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 и y 3 \u003d x 3 ја носи оваа квадратна форма во канонската форма f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Забележете дека канонската форма на квадратна форма е дефинирана двосмислено (истата квадратна форма може да се сведе на канонска форма на различни начини). Сепак, канонските форми добиени со различни методи имаат голем број заеднички својства. Особено, бројот на членови со позитивни (негативни) коефициенти на квадратна форма не зависи од тоа како формата се сведува на оваа форма (на пример, во разгледуваниот пример секогаш ќе има два негативни и еден позитивен коефициент). Ова својство се нарекува закон за инерција на квадратни форми.

Дозволете ни да го потврдиме ова со намалување на истата квадратна форма на канонската форма на поинаков начин. Да ја започнеме трансформацијата со променливата x 2:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, каде што y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6 ) x 3 и y 3 = x 1 . Овде, негативен коефициент -3 на y 1 и два позитивни коефициенти 3 и 2 на y 2 и y 3 (и користејќи друг метод, добивме негативен коефициент (-5) на y 2 и два позитивни коефициенти: 2 на y 1 и 1/20 за y 3).

Исто така, треба да се забележи дека рангот на матрица од квадратна форма, наречен рангот на квадратната форма, е еднаков на бројот на ненулти коефициенти на канонската форма и не се менува при линеарни трансформации.

Се нарекува квадратната форма f(X). позитивно (негативен) одредени, ако за сите вредности на променливите кои не се истовремено еднакви на нула, тоа е позитивно, т.е. f(X) > 0 (негативно, т.е.
f(X)< 0).

На пример, квадратната форма f 1 (X) \u003d x 1 2 + x 2 2 е позитивно определена, бидејќи е збир на квадрати, а квадратната форма f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 е негативна дефинитивна, бидејќи го претставува може да се претстави како f 2 (X) \u003d - (x 1 - x 2) 2.

Во повеќето практични ситуации, нешто потешко е да се утврди знаковно-одреденоста на квадратна форма, па за ова се користи една од следните теореми (ги формулираме без докази).

Теорема. Квадратната форма е позитивна (негативна) дефинитивна ако и само ако сите сопствени вредности на нејзината матрица се позитивни (негативни).

Теорема(Силвестеровиот критериум). Квадратната форма е позитивна дефинитивна ако и само ако сите главни минори од матрицата на оваа форма се позитивни.

Мајор (аголна) мол K-тиот ред на матрицата A од n-тиот ред се нарекува детерминанта на матрицата, составена од првите k редици и колони од матрицата A ().

Имајте на ум дека за негативно-одредени квадратни форми, знаците на главните малолетници се наизменично, а минорот од прв ред мора да биде негативен.

На пример, ја испитуваме квадратната форма f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 за определеност на знакот.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. Според тоа, квадратната форма е позитивна дефинитивна.

Метод 2. Главниот минор од првиот ред на матрицата A D 1 = a 11 = 2 > 0. Главниот минор од вториот ред D 2 = = 6 - 4 = 2 > 0. Затоа, според критериумот Силвестер, квадратната форма е позитивна определена.

Испитуваме друга квадратна форма за определеност на знакот, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Метод 1. Да конструираме матрица со квадратна форма А = . Карактеристичната равенка ќе ја има формата = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Според тоа, квадратната форма е негативна определена.

Метод 2. Главниот минор од првиот ред на матрицата A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Според тоа, според критериумот Силвестер, квадратната форма е негативна определена (знаците на главните малолетници се менуваат, почнувајќи од минус).

И како друг пример, ја испитуваме квадратната форма f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 за дефинитивноста на знакот.

Метод 1. Да конструираме матрица со квадратна форма А = . Карактеристичната равенка ќе ја има формата = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Еден од овие бројки е негативен, а другиот позитивен. Знаците на сопствените вредности се различни. Според тоа, квадратната форма не може да биде ниту негативна ниту позитивна определена, т.е. оваа квадратна форма не е дефинитивна знак (може да земе вредности од кој било знак).

Метод 2. Главниот минор од првиот ред на матрицата A D 1 = a 11 = 2 > 0. Главниот минор од вториот ред D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).