Cari nilai eigen pengendali. Nilai eigen (nombor) dan vektor eigen. Contoh penyelesaian

Matriks pepenjuru mempunyai struktur yang paling mudah. Timbul persoalan sama ada adalah mungkin untuk mencari asas di mana matriks pengendali linear akan mempunyai bentuk pepenjuru. Asas sedemikian wujud.
Marilah kita diberi ruang linear R n dan operator linear A bertindak di dalamnya; dalam kes ini, pengendali A mengambil R n ke dalam dirinya sendiri, iaitu, A:R n → R n .

Definisi. Vektor bukan sifar dipanggil vektor eigen bagi operator A jika operator A menterjemah ke dalam vektor kolinear, iaitu. Nombor λ dipanggil nilai eigen atau nilai eigen bagi operator A, sepadan dengan vektor eigen.
Mari kita perhatikan beberapa sifat nilai eigen dan vektor eigen.
1. Sebarang gabungan linear bagi vektor eigen operator A sepadan dengan nilai eigen yang sama λ ialah vektor eigen dengan nilai eigen yang sama.
2. Eigenvectors operator A dengan nilai eigen berbeza berpasangan λ 1 , λ 2 , …, λ m adalah bebas secara linear.
3. Jika nilai eigen λ 1 =λ 2 = λ m = λ, maka nilai eigen λ sepadan dengan tidak lebih daripada m vektor eigen bebas linear.

Jadi, jika terdapat n vektor eigen bebas linear , sepadan dengan nilai eigen yang berbeza λ 1, λ 2, ..., λ n, maka ia adalah bebas secara linear, oleh itu, ia boleh diambil sebagai asas ruang R n. Mari kita cari bentuk matriks operator linear A dalam asas vektor eigennya, yang mana kita akan bertindak dengan operator A pada vektor asas: Kemudian .
Oleh itu, matriks pengendali linear A berdasarkan vektor eigennya mempunyai bentuk pepenjuru, dan nilai eigen pengendali A berada di sepanjang pepenjuru.
Adakah terdapat asas lain di mana matriks mempunyai bentuk pepenjuru? Jawapan kepada soalan ini diberikan oleh teorem berikut.

Teorem. Matriks pengendali linear A dalam asas (i = 1..n) mempunyai bentuk pepenjuru jika dan hanya jika semua vektor asas ialah vektor eigen bagi operator A.

Peraturan untuk mencari nilai eigen dan vektor eigen

. (*)

(1)
di mana - matriks operator linear.

Sistem (1) mempunyai penyelesaian bukan sifar jika penentunya D adalah sama dengan sifar

Contoh 12. Pengendali linear A bertindak dalam R 3 mengikut undang-undang, di mana x 1, x 2, .., x n ialah koordinat vektor dalam asas , , . Cari nilai eigen dan vektor eigen bagi operator ini.
Penyelesaian. Kami membina matriks pengendali ini:
.
Kami mencipta sistem untuk menentukan koordinat vektor eigen:

Kami menyusun persamaan ciri dan menyelesaikannya:

.
λ 1,2 = -1, λ 3 = 3.
Menggantikan λ = -1 ke dalam sistem, kita mempunyai:
atau
Kerana , maka terdapat dua pembolehubah bersandar dan satu pembolehubah bebas.
Biarkan x 1 menjadi tidak diketahui percuma, kemudian Kami menyelesaikan sistem ini dalam apa jua cara dan mencari penyelesaian umum sistem ini: Sistem asas penyelesaian terdiri daripada satu penyelesaian, kerana n - r = 3 - 2 = 1.
Set vektor eigen sepadan dengan nilai eigen λ = -1 mempunyai bentuk: , di mana x 1 ialah sebarang nombor selain daripada sifar. Mari kita pilih satu vektor daripada set ini, sebagai contoh, meletakkan x 1 = 1: .
Penalaran yang sama, kita dapati vektor eigen sepadan dengan nilai eigen λ = 3: .
Dalam ruang R 3, asasnya terdiri daripada tiga vektor bebas linear, tetapi kami hanya menerima dua vektor eigen bebas linear, yang mana asas dalam R 3 tidak boleh digubah. Akibatnya, kita tidak boleh mengurangkan matriks A operator linear kepada bentuk pepenjuru.

Contoh 13. Diberi matriks .
1. Buktikan bahawa vektor ialah vektor eigen bagi matriks A. Cari nilai eigen yang sepadan dengan vektor eigen ini.
2. Cari asas di mana matriks A mempunyai bentuk pepenjuru.
Penyelesaian.
1. Jika , maka ialah vektor eigen

.
Vektor (1, 8, -1) ialah vektor eigen. Nilai eigen λ = -1.
Matriks mempunyai bentuk pepenjuru dalam asas yang terdiri daripada vektor eigen. Salah seorang daripada mereka terkenal. Mari cari yang lain.
Kami mencari vektor eigen daripada sistem:

Persamaan ciri: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Mari cari vektor eigen yang sepadan dengan nilai eigen λ = -3:

Kedudukan matriks sistem ini ialah dua dan sama dengan bilangan yang tidak diketahui, jadi sistem ini hanya mempunyai penyelesaian sifar x 1 = x 3 = 0. x 2 di sini boleh menjadi apa-apa selain sifar, contohnya, x 2 = 1. Oleh itu, vektor (0 ,1,0) ialah vektor eigen sepadan dengan λ = -3. Mari semak:
.
Jika λ = 1, maka kita memperoleh sistem
Kedudukan matriks ialah dua. Kami memotong persamaan terakhir.
Biarkan x 3 menjadi tidak diketahui percuma. Kemudian x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Dengan mengandaikan x 3 = 1, kita mempunyai (-3,-9,1) - vektor eigen sepadan dengan nilai eigen λ = 1. Semak:

.
Oleh kerana nilai eigen adalah nyata dan berbeza, vektor yang sepadan dengannya adalah bebas secara linear, jadi ia boleh diambil sebagai asas dalam R 3 . Oleh itu, dalam asas , , matriks A mempunyai bentuk:
.
Bukan setiap matriks pengendali linear A:R n → R n boleh dikurangkan kepada bentuk pepenjuru, kerana bagi sesetengah pengendali linear mungkin terdapat kurang daripada n vektor eigen bebas linear. Walau bagaimanapun, jika matriks adalah simetri, maka punca persamaan ciri kedaraban m sepadan dengan betul-betul m vektor bebas linear.

Definisi. Matriks simetri ialah matriks segi empat sama di mana unsur-unsur simetri tentang pepenjuru utama adalah sama, iaitu, di mana .
Nota. 1. Semua nilai eigen bagi matriks simetri adalah nyata.
2. Vektor eigen bagi matriks simetri yang sepadan dengan nilai eigen berbeza berpasangan adalah ortogon.
Sebagai salah satu daripada banyak aplikasi radas yang dikaji, kami mempertimbangkan masalah untuk menentukan jenis lengkung tertib kedua.

Nilai eigen (nombor) dan vektor eigen.
Contoh penyelesaian

Jadi diri sendiri

Daripada kedua-dua persamaan ia mengikuti bahawa .

Mari letakkannya kemudian: .

Akibatnya: – vektor eigen kedua.

Mari kita ulangi perkara penting dalam keputusan itu:

– sistem yang terhasil pasti mempunyai penyelesaian umum (persamaan adalah bergantung secara linear);

– kami memilih "y" sedemikian rupa sehingga ia adalah integer dan koordinat "x" pertama adalah integer, positif dan sekecil mungkin.

– kami menyemak bahawa penyelesaian tertentu memenuhi setiap persamaan sistem.

Jawab .

Terdapat cukup "pusat pemeriksaan" perantaraan, jadi memeriksa kesaksamaan, pada dasarnya, tidak perlu.

Dalam pelbagai sumber maklumat, koordinat vektor eigen sering ditulis bukan dalam lajur, tetapi dalam baris, contohnya: (dan, sejujurnya, saya sendiri sudah biasa menulisnya dalam baris). Pilihan ini boleh diterima, tetapi berdasarkan topik transformasi linear secara teknikal lebih mudah digunakan vektor lajur.

Mungkin penyelesaiannya kelihatan sangat panjang kepada anda, tetapi ini hanya kerana saya mengulas contoh pertama dengan terperinci.

Contoh 2

Matriks

Mari berlatih sendiri! Contoh anggaran tugas akhir pada akhir pelajaran.

Kadangkala anda perlu menyelesaikan tugas tambahan, iaitu:

tulis penguraian matriks kanonik

Apa ini?

Jika vektor eigen bagi matriks membentuk asas, maka ia boleh diwakili sebagai:

Di manakah matriks yang terdiri daripada koordinat vektor eigen, - pepenjuru matriks dengan nilai eigen yang sepadan.

Penguraian matriks ini dipanggil berkanun atau pepenjuru.

Mari kita lihat matriks contoh pertama. vektor eigennya bebas linear(bukan kolinear) dan membentuk asas. Mari kita buat matriks koordinatnya:

hidup pepenjuru utama matriks mengikut susunan yang sesuai nilai eigen terletak, dan elemen yang selebihnya adalah sama dengan sifar:
– Saya sekali lagi menekankan kepentingan susunan: “dua” sepadan dengan vektor pertama dan oleh itu terletak di lajur pertama, “tiga” – kepada vektor ke-2.

Menggunakan algoritma biasa untuk mencari matriks songsang atau Kaedah Gauss-Jordan kita dapati . Tidak, itu bukan kesilapan menaip! - sebelum anda adalah peristiwa yang jarang berlaku, seperti gerhana matahari, apabila sebaliknya bertepatan dengan matriks asal.

Ia kekal untuk menulis penguraian kanonik matriks:

Sistem ini boleh diselesaikan menggunakan transformasi asas, dan dalam contoh berikut kita akan menggunakan kaedah ini. Tetapi di sini kaedah "sekolah" berfungsi lebih cepat. Daripada persamaan ke-3 kita nyatakan: – gantikan ke dalam persamaan kedua:

Oleh kerana koordinat pertama ialah sifar, kita memperoleh satu sistem, daripada setiap persamaan yang mana ia mengikuti bahawa .

Dan lagi memberi perhatian kepada kehadiran wajib hubungan linear. Jika hanya penyelesaian remeh yang diperolehi , maka sama ada nilai eigen didapati salah, atau sistem telah disusun/diselesaikan dengan ralat.

Koordinat padat memberikan nilai

Eigenvector:

Dan sekali lagi, kami menyemak bahawa penyelesaian itu ditemui memenuhi setiap persamaan sistem. Dalam perenggan seterusnya dan dalam tugasan seterusnya, saya mengesyorkan mengambil hasrat ini sebagai peraturan wajib.

2) Untuk nilai eigen, menggunakan prinsip yang sama, kami memperoleh sistem berikut:

Daripada persamaan ke-2 sistem kita nyatakan: – gantikan ke dalam persamaan ketiga:

Oleh kerana koordinat "zeta" adalah sama dengan sifar, kami memperoleh sistem daripada setiap persamaan yang mana pergantungan linear mengikutinya.

biarlah

Menyemak bahawa penyelesaian memenuhi setiap persamaan sistem.

Oleh itu, vektor eigen ialah: .

3) Dan akhirnya, sistem sepadan dengan nilai eigen:

Persamaan kedua kelihatan paling mudah, jadi mari kita nyatakan dan gantikannya ke dalam persamaan 1 dan 3:

Semuanya baik-baik saja - hubungan linear telah muncul, yang kita gantikan ke dalam ungkapan:

Akibatnya, "x" dan "y" dinyatakan melalui "z": . Dalam amalan, tidak perlu untuk mencapai perhubungan sedemikian dengan tepat; dalam beberapa kes, lebih mudah untuk menyatakan kedua-dua melalui atau dan melalui . Atau pun "kereta api" - contohnya, "X" melalui "I", dan "I" melalui "Z"

Mari letakkannya kemudian:

Kami menyemak bahawa penyelesaian itu ditemui memenuhi setiap persamaan sistem dan menulis vektor eigen ketiga

Jawab: vektor eigen:

Secara geometri, vektor ini mentakrifkan tiga arah spatial yang berbeza ("Di sana dan kembali lagi"), mengikut mana transformasi linear menukarkan vektor bukan sifar (eigenvectors) kepada vektor kolinear.

Jika keadaan memerlukan mencari penguraian kanonik, maka ini mungkin di sini, kerana nilai eigen yang berbeza sepadan dengan vektor eigen bebas linear yang berbeza. Membuat matriks daripada koordinat mereka, matriks pepenjuru daripada relevan nilai eigen dan cari matriks songsang .

Jika, dengan syarat, anda perlu menulis matriks transformasi linear dalam asas vektor eigen, kemudian kita berikan jawapan dalam borang . Terdapat perbezaan, dan perbezaannya adalah ketara! Kerana matriks ini adalah matriks "de".

Masalah dengan pengiraan yang lebih mudah untuk anda selesaikan sendiri:

Contoh 5

Cari vektor eigen bagi penjelmaan linear yang diberikan oleh matriks

Apabila mencari nombor anda sendiri, cuba jangan pergi sepenuhnya ke polinomial darjah 3. Di samping itu, penyelesaian sistem anda mungkin berbeza daripada penyelesaian saya - tiada kepastian di sini; dan vektor yang anda temui mungkin berbeza daripada vektor sampel sehingga kekadaran koordinat masing-masing. Contohnya, dan. Ia lebih menyenangkan dari segi estetika untuk membentangkan jawapan dalam borang, tetapi tidak mengapa jika anda berhenti pada pilihan kedua. Walau bagaimanapun, terdapat had yang munasabah untuk segala-galanya; versi tidak lagi kelihatan sangat baik.

Anggaran sampel akhir tugasan pada akhir pelajaran.

Bagaimana untuk menyelesaikan masalah dalam kes pelbagai nilai eigen?

Algoritma umum tetap sama, tetapi ia mempunyai ciri tersendiri, dan dinasihatkan untuk mengekalkan beberapa bahagian penyelesaian dalam gaya akademik yang lebih ketat:

Contoh 6

Cari nilai eigen dan vektor eigen

Penyelesaian

Sudah tentu, mari gunakan huruf besar lajur pertama yang hebat:

Dan, selepas memfaktorkan trinomial kuadratik:

Akibatnya, nilai eigen diperoleh, dua daripadanya adalah gandaan.

Mari cari vektor eigen:

1) Mari kita berurusan dengan askar keseorangan mengikut skema "dipermudahkan":

Daripada dua persamaan terakhir, kesamaan jelas kelihatan, yang, jelas, harus digantikan ke dalam persamaan pertama sistem:

Anda tidak akan menemui gabungan yang lebih baik:
Eigenvector:

2-3) Sekarang kita keluarkan beberapa sentri. Dalam kes ini ia mungkin berubah sama ada dua atau satu eigenvector. Tanpa mengira kepelbagaian akar, kami menggantikan nilai ke dalam penentu yang membawa kita seterusnya sistem persamaan linear homogen:

Eigenvectors adalah betul-betul vektor
sistem asas penyelesaian

Sebenarnya, sepanjang keseluruhan pelajaran kami tidak melakukan apa-apa selain mencari vektor sistem asas. Cuma buat masa ini istilah ini tidak diperlukan secara khusus. Ngomong-ngomong, pelajar pintar yang terlepas topik dalam sut penyamaran persamaan homogen, akan terpaksa menghisapnya sekarang.

Satu-satunya tindakan ialah mengeluarkan garisan tambahan. Hasilnya ialah matriks satu demi tiga dengan "langkah" formal di tengah.
– pembolehubah asas, – pembolehubah bebas. Oleh itu, terdapat dua pembolehubah bebas terdapat juga dua vektor sistem asas.

Mari kita nyatakan pembolehubah asas dari segi pembolehubah bebas: . Pengganda sifar di hadapan "X" membolehkannya mengambil apa-apa nilai (yang jelas kelihatan dari sistem persamaan).

Dalam konteks masalah ini, lebih mudah untuk menulis penyelesaian umum bukan dalam baris, tetapi dalam lajur:

Pasangan sepadan dengan vektor eigen:
Pasangan sepadan dengan vektor eigen:

Catatan : pembaca yang canggih boleh memilih vektor ini secara lisan - hanya dengan menganalisis sistem , tetapi beberapa pengetahuan diperlukan di sini: terdapat tiga pembolehubah, kedudukan matriks sistem- satu, yang bermaksud sistem keputusan asas terdiri daripada 3 – 1 = 2 vektor. Walau bagaimanapun, vektor yang ditemui jelas kelihatan walaupun tanpa pengetahuan ini, semata-mata pada tahap intuitif. Dalam kes ini, vektor ketiga akan ditulis dengan lebih "cantik": . Walau bagaimanapun, saya memberi amaran kepada anda bahawa dalam contoh lain, pemilihan mudah mungkin tidak boleh dilakukan, itulah sebabnya klausa itu ditujukan untuk orang yang berpengalaman. Di samping itu, mengapa tidak mengambil, katakan, sebagai vektor ketiga? Lagipun, koordinatnya juga memenuhi setiap persamaan sistem, dan vektor bebas linear. Pilihan ini, pada dasarnya, sesuai, tetapi "bengkok", kerana vektor "lain" ialah gabungan linear vektor sistem asas.

Jawab: nilai eigen: , vektor eigen:

Contoh serupa untuk penyelesaian bebas:

Contoh 7

Cari nilai eigen dan vektor eigen

Contoh anggaran reka bentuk akhir pada akhir pelajaran.

Perlu diingatkan bahawa dalam kedua-dua contoh ke-6 dan ke-7, tiga kali ganda vektor eigen bebas linear diperoleh, dan oleh itu matriks asal boleh diwakili dalam penguraian kanonik. Tetapi raspberi seperti itu tidak berlaku dalam semua kes:

Contoh 8

Penyelesaian: Mari cipta dan selesaikan persamaan ciri:

Mari kembangkan penentu dalam lajur pertama:

Kami menjalankan penyederhanaan lanjut mengikut kaedah yang dipertimbangkan, mengelakkan polinomial darjah ketiga:

– nilai eigen.

Mari cari vektor eigen:

1) Tiada masalah dengan akar:

Jangan terkejut, sebagai tambahan kepada kit, terdapat juga pembolehubah yang digunakan - tidak ada perbezaan di sini.

Daripada persamaan ke-3 kita menyatakannya dan menggantikannya ke dalam persamaan ke-1 dan ke-2:

Daripada kedua-dua persamaan berikut:

Biarkan kemudian:

2-3) Untuk pelbagai nilai, kami mendapat sistem .

Mari kita tuliskan matriks sistem dan, menggunakan transformasi asas, bawa ia ke bentuk berperingkat:

www.site membolehkan anda mencari . Tapak melakukan pengiraan. Dalam beberapa saat pelayan akan memberikan penyelesaian yang betul. Persamaan ciri untuk matriks akan menjadi ungkapan algebra yang ditemui menggunakan peraturan untuk mengira penentu matriks matriks, manakala di sepanjang pepenjuru utama akan terdapat perbezaan dalam nilai unsur pepenjuru dan pembolehubah. Apabila mengira persamaan ciri untuk matriks dalam talian, setiap elemen matriks akan didarab dengan unsur-unsur lain yang sepadan matriks. Cari dalam mod dalam talian hanya mungkin untuk persegi matriks. Operasi mencari persamaan ciri untuk matriks dalam talian berkurang untuk mengira jumlah algebra hasil darab unsur matriks hasil daripada mencari penentu matriks, hanya untuk tujuan menentukan persamaan ciri untuk matriks dalam talian. Operasi ini menduduki tempat yang istimewa dalam teori matriks, membolehkan anda mencari nilai eigen dan vektor menggunakan akar. Tugas mencari persamaan ciri untuk matriks dalam talian terdiri daripada unsur pendaraban matriks diikuti dengan menjumlahkan produk ini mengikut peraturan tertentu. www.site jumpa persamaan ciri untuk matriks dimensi yang diberikan dalam mod dalam talian. Pengiraan persamaan ciri untuk matriks dalam talian memandangkan dimensinya, ini adalah mencari polinomial dengan pekali berangka atau simbolik, ditemui mengikut peraturan untuk mengira penentu matriks- sebagai jumlah hasil darab unsur yang sepadan matriks, hanya untuk tujuan menentukan persamaan ciri untuk matriks dalam talian. Mencari polinomial berkenaan dengan pembolehubah bagi kuadratik matriks, sebagai definisi persamaan ciri untuk matriks, biasa dalam teori matriks. Maksud akar bagi polinomial persamaan ciri untuk matriks dalam talian digunakan untuk menentukan vektor eigen dan nilai eigen untuk matriks. Lebih-lebih lagi jika penentu matriks akan sama dengan sifar, maka persamaan ciri matriks akan tetap wujud, tidak seperti sebaliknya matriks. Untuk mengira persamaan ciri untuk matriks atau cari beberapa sekali gus persamaan ciri matriks, anda perlu menghabiskan banyak masa dan usaha, manakala pelayan kami akan mencari dalam masa beberapa saat persamaan ciri untuk matriks dalam talian. Dalam kes ini, jawapan untuk mencari persamaan ciri untuk matriks dalam talian akan betul dan dengan ketepatan yang mencukupi, walaupun nombor semasa mencari persamaan ciri untuk matriks dalam talian akan menjadi tidak rasional. Di tapak www.site entri aksara dibenarkan dalam elemen matriks, itu dia persamaan ciri untuk matriks dalam talian boleh diwakili dalam bentuk simbolik umum semasa mengira persamaan ciri matriks dalam talian. Adalah berguna untuk menyemak jawapan yang diperoleh semasa menyelesaikan masalah mencari persamaan ciri untuk matriks dalam talian menggunakan tapak www.site. Apabila melakukan operasi pengiraan polinomial - persamaan ciri matriks, anda perlu berhati-hati dan sangat fokus apabila menyelesaikan masalah ini. Sebaliknya, laman web kami akan membantu anda menyemak keputusan anda mengenai topik tersebut persamaan ciri matriks dalam talian. Jika anda tidak mempunyai masa untuk pemeriksaan panjang masalah yang diselesaikan, maka www.site pastinya akan menjadi alat yang mudah untuk menyemak apabila mencari dan mengira persamaan ciri untuk matriks dalam talian.

Vektor eigen bagi matriks segi empat sama ialah, apabila didarab dengan matriks tertentu, menghasilkan vektor kolinear. Dalam kata mudah, apabila matriks didarab dengan vektor eigen, yang terakhir tetap sama, tetapi didarab dengan nombor tertentu.

Definisi

Vektor eigen ialah vektor bukan sifar V, yang, apabila didarab dengan matriks persegi M, menjadi sendiri meningkat dengan beberapa nombor λ. Dalam tatatanda algebra ia kelihatan seperti:

M × V = λ × V,

di mana λ ialah nilai eigen bagi matriks M.

Mari kita lihat contoh berangka. Untuk memudahkan rakaman, nombor dalam matriks akan dipisahkan dengan koma bertitik. Mari kita mempunyai matriks:

• M = 0; 4;
• 6; 10.

Mari kita darabkannya dengan vektor lajur:

• V = -2;

Apabila kita mendarab matriks dengan vektor lajur, kita juga mendapat vektor lajur. Dalam bahasa matematik yang ketat, formula untuk mendarab matriks 2 × 2 dengan vektor lajur akan kelihatan seperti ini:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 bermaksud elemen matriks M yang terletak di baris pertama dan lajur pertama, dan M22 bermaksud elemen yang terletak di baris kedua dan lajur kedua. Untuk matriks kami, unsur-unsur ini adalah sama dengan M11 = 0, M12 = 4, M21 = 6, M22 10. Untuk vektor lajur, nilai-nilai ini adalah sama dengan V11 = –2, V21 = 1. Menurut formula ini, kita mendapat keputusan berikut hasil darab matriks segi empat sama dengan vektor:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Untuk kemudahan, mari tulis vektor lajur ke dalam satu baris. Jadi, kami mendarabkan matriks segi empat sama dengan vektor (-2; 1), menghasilkan vektor (4; -2). Jelas sekali, ini adalah vektor yang sama didarab dengan λ = -2. Lambda dalam kes ini menandakan nilai eigen bagi matriks.

Vektor eigen bagi matriks ialah vektor kolinear, iaitu objek yang tidak mengubah kedudukannya dalam ruang apabila didarab dengan matriks. Konsep kolineariti dalam algebra vektor adalah serupa dengan istilah keselarian dalam geometri. Dalam tafsiran geometri, vektor kolinear ialah segmen terarah selari dengan panjang yang berbeza. Sejak zaman Euclid, kita tahu bahawa satu baris mempunyai bilangan garis tak terhingga yang selari dengannya, jadi adalah logik untuk mengandaikan bahawa setiap matriks mempunyai bilangan vektor eigen yang tidak terhingga.

Daripada contoh sebelumnya adalah jelas bahawa vektor eigen boleh menjadi (-8; 4), dan (16; -8), dan (32, -16). Ini semua adalah vektor kolinear sepadan dengan nilai eigen λ = -2. Apabila mendarab matriks asal dengan vektor ini, kita masih akan berakhir dengan vektor yang berbeza daripada asal sebanyak 2 kali. Itulah sebabnya, apabila menyelesaikan masalah mencari vektor eigen, adalah perlu untuk mencari hanya objek vektor bebas linear. Selalunya, untuk matriks n × n, terdapat n bilangan vektor eigen. Kalkulator kami direka bentuk untuk analisis matriks segi empat sama tertib kedua, jadi hampir selalu hasilnya akan menemui dua vektor eigen, kecuali untuk kes apabila ia bertepatan.

Dalam contoh di atas, kami mengetahui vektor eigen bagi matriks asal terlebih dahulu dan menentukan nombor lambda dengan jelas. Walau bagaimanapun, dalam amalan, segala-galanya berlaku sebaliknya: nilai eigen ditemui dahulu dan barulah vektor eigen.

Algoritma penyelesaian

Mari kita lihat semula matriks asal M dan cuba cari kedua-dua vektor eigennya. Jadi matriks kelihatan seperti:

• M = 0; 4;
• 6; 10.

Mula-mula kita perlu menentukan nilai eigen λ, yang memerlukan pengiraan penentu matriks berikut:

• (0 − λ); 4;
• 6; (10 − λ).

Matriks ini diperoleh dengan menolak λ yang tidak diketahui daripada unsur-unsur pada pepenjuru utama. Penentu ditentukan menggunakan formula piawai:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Oleh kerana vektor kami mestilah bukan sifar, kami menerima persamaan yang terhasil sebagai bersandar secara linear dan menyamakan detA penentu kami kepada sifar.

(0 − λ) × (10 − λ) − 24 = 0

Mari buka kurungan dan dapatkan persamaan ciri matriks:

λ 2 − 10λ − 24 = 0

Ini ialah persamaan kuadratik piawai yang perlu diselesaikan menggunakan diskriminasi.

D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

Punca diskriminasi ialah sqrt(D) = 14, oleh itu λ1 = -2, λ2 = 12. Sekarang untuk setiap nilai lambda kita perlu mencari vektor eigen. Mari kita nyatakan pekali sistem untuk λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

Dalam formula ini, E ialah matriks identiti. Berdasarkan matriks yang terhasil, kami mencipta sistem persamaan linear:

2x + 4y = 6x + 12y,

dengan x dan y ialah unsur vektor eigen.

Mari kumpulkan semua X di sebelah kiri dan semua Y di sebelah kanan. Jelas sekali - 4x = 8y. Bahagikan ungkapan dengan - 4 dan dapatkan x = –2y. Sekarang kita boleh menentukan vektor eigen pertama matriks, mengambil sebarang nilai yang tidak diketahui (ingat infiniti vektor eigen yang bergantung secara linear). Mari kita ambil y = 1, kemudian x = –2. Oleh itu, vektor eigen pertama kelihatan seperti V1 = (–2; 1). Kembali ke permulaan artikel. Objek vektor inilah yang kami darabkan dengan matriks untuk menunjukkan konsep vektor eigen.

Sekarang mari kita cari vektor eigen untuk λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Mari kita cipta sistem persamaan linear yang sama;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x = y.

Sekarang kita ambil x = 1, oleh itu y = 3. Oleh itu, vektor eigen kedua kelihatan seperti V2 = (1; 3). Apabila mendarab matriks asal dengan vektor tertentu, hasilnya akan sentiasa menjadi vektor yang sama didarab dengan 12. Di sinilah algoritma penyelesaian berakhir. Sekarang anda tahu cara menentukan vektor eigen bagi matriks secara manual.

• penentu;
• surih, iaitu jumlah unsur pada pepenjuru utama;
• pangkat, iaitu bilangan maksimum baris/lajur bebas linear.

Program ini beroperasi mengikut algoritma di atas, memendekkan proses penyelesaian sebanyak mungkin. Adalah penting untuk menunjukkan bahawa dalam program lambda ditetapkan oleh huruf "c". Mari kita lihat contoh berangka.

Contoh bagaimana program ini berfungsi

Mari cuba tentukan vektor eigen untuk matriks berikut:

• M = 5; 13;
• 4; 14.

Mari masukkan nilai ini ke dalam sel kalkulator dan dapatkan jawapan dalam bentuk berikut:

• Kedudukan matriks: 2;
• Penentu matriks: 18;
• Surih matriks: 19;
• Pengiraan vektor eigen: c 2 − 19.00c + 18.00 (persamaan ciri);
• Pengiraan vektor eigen: 18 (nilai lambda pertama);
• Pengiraan vektor eigen: 1 (nilai lambda kedua);
• Sistem persamaan untuk vektor 1: -13x1 + 13y1 = 4x1 − 4y1;
• Sistem persamaan untuk vektor 2: 4x1 + 13y1 = 4x1 + 13y1;
• Eigenvector 1: (1; 1);
• Eigenvector 2: (-3.25; 1).

Oleh itu, kami memperoleh dua vektor eigen bebas linear.

Kesimpulan

Algebra linear dan geometri analitik adalah mata pelajaran standard untuk mana-mana pelajar kejuruteraan baru. Bilangan besar vektor dan matriks adalah menakutkan, dan mudah untuk membuat kesilapan dalam pengiraan yang menyusahkan itu. Program kami akan membolehkan pelajar menyemak pengiraan mereka atau menyelesaikan masalah mencari vektor eigen secara automatik. Terdapat kalkulator algebra linear lain dalam katalog kami; gunakannya dalam pengajian atau kerja anda.

"Bahagian pertama menetapkan peruntukan yang paling minimum diperlukan untuk memahami kemometrik, dan bahagian kedua mengandungi fakta yang perlu anda ketahui untuk pemahaman yang lebih mendalam tentang kaedah analisis multivariate. Pembentangan digambarkan dengan contoh yang dibuat dalam buku kerja Excel Matriks.xls, yang disertakan bersama dokumen ini.

Pautan kepada contoh diletakkan dalam teks sebagai objek Excel. Contoh-contoh ini bersifat abstrak; mereka sama sekali tidak terikat dengan masalah kimia analitik. Contoh kehidupan sebenar penggunaan algebra matriks dalam kemometrik dibincangkan dalam teks lain yang meliputi pelbagai aplikasi kemometrik.

Kebanyakan pengukuran yang dibuat dalam kimia analitik tidak langsung, tetapi tidak langsung. Ini bermakna dalam eksperimen, bukannya nilai analit C (kepekatan) yang dikehendaki, nilai lain diperolehi x(isyarat), berkaitan tetapi tidak sama dengan C, i.e. x(C) ≠ C. Sebagai peraturan, jenis pergantungan x(C) tidak diketahui, tetapi mujurlah dalam kimia analitik kebanyakan ukuran adalah berkadar. Ini bermakna dengan peningkatan kepekatan C dalam a kali, isyarat X akan meningkat dengan jumlah yang sama, i.e. x(a C) = a x(C). Di samping itu, isyarat juga adalah aditif, jadi isyarat daripada sampel di mana dua bahan dengan kepekatan C 1 dan C 2 hadir akan sama dengan jumlah isyarat daripada setiap komponen, i.e. x(C 1 + C 2) = x(C 1)+ x(C 2). Perkadaran dan ketambahan bersama-sama memberi kelinearan. Banyak contoh boleh diberikan untuk menggambarkan prinsip lineariti, tetapi cukup untuk menyebut dua contoh yang paling menarik - kromatografi dan spektroskopi. Ciri kedua yang wujud dalam eksperimen dalam kimia analitik ialah berbilang saluran. Peralatan analisis moden secara serentak mengukur isyarat untuk banyak saluran. Sebagai contoh, keamatan penghantaran cahaya diukur untuk beberapa panjang gelombang sekaligus, i.e. julat. Oleh itu, dalam eksperimen kita berurusan dengan banyak isyarat x 1 , x 2 ,...., x n, mencirikan set kepekatan C 1 , C 2 , ..., C m bahan yang terdapat dalam sistem yang dikaji.

nasi. 1 Spektrum

Jadi, eksperimen analitik dicirikan oleh lineariti dan multidimensi. Oleh itu, adalah mudah untuk mempertimbangkan data eksperimen sebagai vektor dan matriks dan memanipulasinya menggunakan radas algebra matriks. Keberhasilan pendekatan ini digambarkan oleh contoh yang ditunjukkan dalam, yang membentangkan tiga spektrum yang diambil pada 200 panjang gelombang dari 4000 hingga 4796 cm -1. pertama ( x 1) dan kedua ( x 2) spektrum diperolehi untuk sampel standard di mana kepekatan dua bahan A dan B diketahui: dalam sampel pertama [A] = 0.5, [B] = 0.1, dan dalam sampel kedua [A] = 0.2, [ B] = 0.6. Apa yang boleh dikatakan tentang sampel baru yang tidak diketahui, spektrumnya ditunjukkan x 3 ?

Mari kita pertimbangkan tiga spektrum eksperimen x 1 , x 2 dan x 3 sebagai tiga vektor dimensi 200. Menggunakan algebra linear, seseorang boleh menunjukkannya dengan mudah x 3 = 0.1 x 1 +0.3 x 2, jadi sampel ketiga jelas mengandungi hanya bahan A dan B dalam kepekatan [A] = 0.5×0.1 + 0.2×0.3 = 0.11 dan [B] = 0.1×0.1 + 0.6×0.3 = 0.19.

1. Maklumat asas

1.1 Matriks

Matriks dipanggil jadual nombor segi empat tepat, contohnya

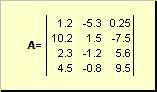
nasi. 2 Matriks

Matriks dilambangkan dengan huruf tebal besar ( A), dan elemennya - dengan huruf kecil yang sepadan dengan indeks, i.e. a ij. Indeks pertama menomborkan baris, dan yang kedua - lajur. Dalam kemometrik, adalah kebiasaan untuk menunjukkan nilai maksimum indeks dengan huruf yang sama dengan indeks itu sendiri, tetapi dalam huruf besar. Oleh itu matriks A boleh juga ditulis sebagai ( a ij , i = 1,..., saya; j = 1,..., J). Untuk contoh matriks saya = 4, J= 3 dan a 23 = −7.5.

Sepasang nombor saya Dan J dipanggil dimensi matriks dan dilambangkan sebagai saya× J. Contoh matriks dalam kemometrik ialah set spektrum yang diperolehi untuk saya sampel untuk J panjang gelombang.

1.2. Operasi paling mudah dengan matriks

Matriks boleh darab dengan nombor. Dalam kes ini, setiap elemen didarab dengan nombor ini. Sebagai contoh -

nasi. 3 Mendarab matriks dengan nombor

Dua matriks yang sama dimensi boleh menjadi unsur demi unsur lipat Dan tolak. Sebagai contoh,

nasi. 4 Penambahan matriks

Hasil daripada pendaraban dengan nombor dan penambahan, matriks yang sama dimensi diperolehi.

Matriks sifar ialah matriks yang terdiri daripada sifar. Ia ditetapkan O. Ia adalah jelas bahawa A+O = A, A−A = O dan 0 A = O.

Matriks boleh transpose. Semasa operasi ini, matriks terbalik, i.e. baris dan lajur ditukar. Transposisi ditunjukkan oleh perdana, A" atau indeks A t. Justeru, jika A = {a ij , i = 1,..., saya; j = 1,...,J), Itu A t = ( a ji , j = 1,...,J; i = 1,..., saya). Sebagai contoh

nasi. 5 Transposisi matriks

Jelas sekali bahawa ( A t) t = A, (A+B)t = A t+ B t.

1.3. Pendaraban matriks

Matriks boleh membiak, tetapi hanya jika mereka mempunyai dimensi yang sesuai. Mengapa ini berlaku akan jelas dari definisi. Produk matriks A, dimensi saya× K, dan matriks B, dimensi K× J, dipanggil matriks C, dimensi saya× J, yang unsurnya ialah nombor

Oleh itu untuk produk AB adalah perlu bahawa bilangan lajur dalam matriks kiri A adalah sama dengan bilangan baris dalam matriks kanan B. Contoh produk matriks -

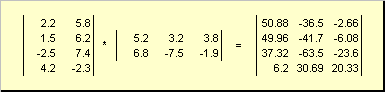
Rajah.6 Hasil darab matriks

Peraturan untuk pendaraban matriks boleh dirumuskan seperti berikut. Untuk mencari unsur matriks C, berdiri di persimpangan i-baris ke- dan j lajur ke ( c ij) mesti didarabkan unsur demi unsur i-baris ke- matriks pertama A pada j lajur ke matriks kedua B dan tambah semua hasil. Jadi dalam contoh yang ditunjukkan, elemen dari baris ketiga dan lajur kedua diperoleh sebagai hasil tambah hasil dari unsur-unsur baris ketiga A dan lajur kedua B

Rajah 7 Unsur hasil darab matriks

Hasil darab matriks bergantung pada susunan, i.e. AB ≠ B.A., sekurang-kurangnya atas sebab dimensi. Mereka mengatakan bahawa ia tidak komutatif. Walau bagaimanapun, hasil darab matriks adalah bersekutu. Maksudnya begitu ABC = (AB)C = A(B.C.). Di samping itu, ia juga pengedaran, i.e. A(B+C) = AB+A.C.. Ia adalah jelas bahawa A.O. = O.

1.4. Matriks segi empat sama

Jika bilangan lajur matriks sama dengan bilangan barisnya ( saya = J=N), maka matriks sedemikian dipanggil segi empat sama. Dalam bahagian ini kita hanya akan mempertimbangkan matriks sedemikian. Di antara matriks ini, matriks dengan sifat khas boleh dibezakan.

Bujang matriks (ditandakan saya, dan kadangkala E) ialah matriks di mana semua elemen adalah sama dengan sifar, kecuali yang pepenjuru, yang sama dengan 1, i.e.

Jelas sekali A.I. = I.A. = A.

Matriks dipanggil pepenjuru, jika semua elemennya kecuali yang menyerong ( a ii) adalah sama dengan sifar. Sebagai contoh

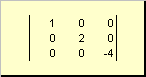
nasi. 8 Matriks pepenjuru

Matriks A dipanggil atas segi tiga, jika semua elemennya yang terletak di bawah pepenjuru adalah sama dengan sifar, i.e. a ij= 0, pada i>j. Sebagai contoh

nasi. 9 Matriks segi tiga atas

Matriks segi tiga yang lebih rendah ditakrifkan sama.

Matriks A dipanggil simetri, Jika A t = A. Dalam kata lain a ij = a ji. Sebagai contoh

nasi. 10 Matriks simetri

Matriks A dipanggil ortogon, Jika

A t A = A.A. t = saya.

Matriks dipanggil biasa Jika

1.5. Jejak dan penentu

Seterusnya matriks segi empat sama A(dilambangkan dengan Tr( A) atau Sp( A)) ialah jumlah unsur pepenjurunya,

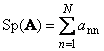
Sebagai contoh,

nasi. 11 Surih matriks

Ia adalah jelas bahawa

Sp(α A) = α Sp( A) Dan

Sp( A+B) = Sp( A)+ Sp( B).

Ia boleh ditunjukkan bahawa

Sp( A) = Sp( A t), Sp( saya) = N,

dan juga itu

Sp( AB) = Sp( B.A.).

Satu lagi ciri penting matriks segi empat sama ialah penentu(ditandakan det( A)). Menentukan penentu dalam kes umum agak sukar, jadi kami akan mulakan dengan pilihan paling mudah - matriks A dimensi (2×2). Kemudian

Untuk matriks (3×3) penentu akan sama dengan

Dalam kes matriks ( N× N) penentu dikira sebagai jumlah 1·2·3· ... · N= N! istilah, setiap satunya adalah sama

Indeks k 1 , k 2 ,..., k N ditakrifkan sebagai semua pilih atur tertib yang mungkin r nombor dalam set (1, 2, ..., N). Mengira penentu matriks adalah prosedur yang kompleks, yang dalam praktiknya dijalankan menggunakan program khas. Sebagai contoh,

nasi. 12 Penentu matriks

Mari kita perhatikan hanya sifat yang jelas:

det( saya) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. vektor

Jika matriks hanya terdiri daripada satu lajur ( J= 1), maka objek sedemikian dipanggil vektor. Lebih tepat lagi, vektor lajur. Sebagai contoh

Seseorang juga boleh mempertimbangkan matriks yang terdiri daripada satu baris, sebagai contoh

Objek ini juga merupakan vektor, tetapi vektor baris. Apabila menganalisis data, adalah penting untuk memahami vektor yang kita hadapi - lajur atau baris. Jadi spektrum yang diambil untuk satu sampel boleh dianggap sebagai vektor baris. Kemudian set keamatan spektrum pada panjang gelombang tertentu untuk semua sampel hendaklah dianggap sebagai vektor lajur.

Dimensi vektor ialah bilangan elemennya.

Adalah jelas bahawa mana-mana vektor lajur boleh ditukar menjadi vektor baris dengan transposisi, i.e.

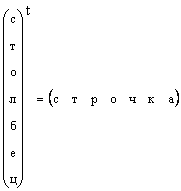
Dalam kes di mana bentuk vektor tidak dinyatakan secara khusus, tetapi hanya dikatakan sebagai vektor, maka ia bermaksud vektor lajur. Kami juga akan mematuhi peraturan ini. Vektor dilambangkan dengan huruf kecil, tegak, huruf tebal. Vektor sifar ialah vektor yang kesemua elemennya adalah sifar. Ia ditetapkan 0 .

1.7. Operasi paling mudah dengan vektor

Vektor boleh ditambah dan didarab dengan nombor dengan cara yang sama seperti matriks. Sebagai contoh,

nasi. 13 Operasi dengan vektor

Dua vektor x Dan y dipanggil kolinear, jika terdapat nombor α sedemikian

1.8. Produk vektor

Dua vektor yang sama dimensi N boleh berganda. Biar ada dua vektor x = (x 1 , x 2 ,...,x N)t dan y = (y 1 , y 2 ,...,y N) t . Berpandukan peraturan pendaraban baris demi lajur, kita boleh mengarang dua produk daripadanya: x t y Dan xy t. Kerja pertama

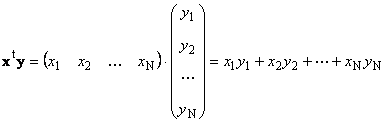
dipanggil skalar atau dalaman. Hasilnya ialah nombor. Ia juga dilambangkan dengan ( x,y)= x t y. Sebagai contoh,

nasi. 14 Hasil kali dalam (skalar).

Sekeping kedua

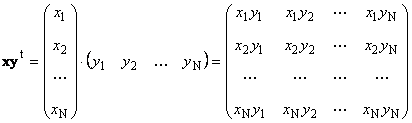
dipanggil luaran. Hasilnya ialah matriks dimensi ( N× N). Sebagai contoh,

nasi. 15 Kerja luaran

Vektor yang hasil darabnya sifar dipanggil ortogon.

1.9. Norma vektor

Hasil darab skalar bagi vektor dengan dirinya sendiri dipanggil kuasa dua skalar. Nilai ini

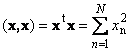
mentakrifkan segi empat sama panjang vektor x. Untuk menunjukkan panjang (juga dipanggil kebiasaan vektor) notasi digunakan

Sebagai contoh,

nasi. 16 Norma vektor

Vektor panjang unit (|| x|| = 1) dipanggil dinormalisasi. Vektor bukan sifar ( x ≠ 0 ) boleh dinormalkan dengan membahagikannya dengan panjang, i.e. x = ||x|| (x/||x||) = ||x|| e. Di sini e = x/||x|| - vektor dinormalkan.

Vektor dipanggil ortonormal jika semuanya dinormalisasi dan ortogon berpasangan.

1.10. Sudut antara vektor

Hasil kali skalar menentukan dan sudutφ antara dua vektor x Dan y

Jika vektor adalah ortogon, maka cosφ = 0 dan φ = π/2, dan jika ia adalah kolinear, maka cosφ = 1 dan φ = 0.

1.11. Perwakilan vektor bagi matriks

Setiap matriks A saiz saya× J boleh diwakili sebagai satu set vektor

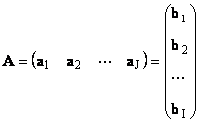
Di sini setiap vektor a j ialah j lajur ke-, dan vektor baris b i ialah i baris ke matriks A

1.12. Vektor bersandar linear

Vektor dengan dimensi yang sama ( N) boleh ditambah dan didarab dengan nombor, sama seperti matriks. Hasilnya akan menjadi vektor dengan dimensi yang sama. Biarkan terdapat beberapa vektor dengan dimensi yang sama x 1 , x 2 ,...,x K dan bilangan nombor yang sama α α 1 , α 2 ,...,α K. vektor

y= α 1 x 1 + α 2 x 2 +...+ α K x K

dipanggil gabungan linear vektor x k .

Jika terdapat nombor bukan sifar α tersebut k ≠ 0, k = 1,..., K, Apa y = 0 , maka set vektor sedemikian x k dipanggil bergantung secara linear. Jika tidak, vektor dikatakan bebas linear. Contohnya, vektor x 1 = (2, 2)t dan x 2 = (−1, −1) t adalah bersandar secara linear, kerana x 1 +2x 2 = 0

1.13. Kedudukan matriks

Pertimbangkan satu set K vektor x 1 , x 2 ,...,x K dimensi N. Kedudukan sistem vektor ini ialah bilangan maksimum vektor bebas linear. Contohnya dalam set

terdapat hanya dua vektor bebas linear, sebagai contoh x 1 dan x 2, jadi pangkatnya ialah 2.

Jelas sekali, jika terdapat lebih banyak vektor dalam satu set daripada dimensinya ( K>N), maka mereka semestinya bergantung secara linear.

Kedudukan matriks(dilambangkan dengan pangkat ( A)) ialah pangkat sistem vektor yang mana ia terdiri. Walaupun mana-mana matriks boleh diwakili dalam dua cara (vektor lajur atau baris), ini tidak menjejaskan nilai kedudukan, kerana

1.14. matriks songsang

Matriks segi empat sama A dipanggil tidak merosot jika ia mempunyai unik terbalik matriks A-1, ditentukan oleh syarat

A.A. −1 = A −1 A = saya.

Matriks songsang tidak wujud untuk semua matriks. Syarat yang perlu dan mencukupi untuk tidak degenerasi ialah

det( A) ≠ 0 atau pangkat( A) = N.

Penyongsangan matriks ialah prosedur kompleks yang mana terdapat program khas. Sebagai contoh,

nasi. 17 Penyongsangan matriks

Mari kita kemukakan formula untuk kes termudah - matriks 2×2

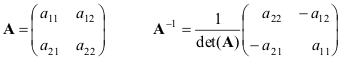
Jika matriks A Dan B tidak merosot, maka

(AB) −1 = B −1 A −1 .

1.15. Matriks pseudoinverse

Jika matriks A adalah tunggal dan matriks songsang tidak wujud, maka dalam beberapa kes anda boleh menggunakan pseudoinverse matriks, yang ditakrifkan sebagai matriks sedemikian A+ itu

A.A. + A = A.

Matriks pseudoinverse bukan satu-satunya dan bentuknya bergantung pada kaedah pembinaan. Sebagai contoh, untuk matriks segi empat tepat anda boleh menggunakan kaedah Moore-Penrose.

Jika bilangan lajur kurang daripada bilangan baris, maka

A + =(A t A) −1 A t

Sebagai contoh,

nasi. 17a Pseudo-penyongsangan matriks

Jika bilangan lajur lebih besar daripada bilangan baris, maka

A + =A t ( A.A. t) −1

1.16. Mendarab vektor dengan matriks

vektor x boleh didarab dengan matriks A saiz yang sesuai. Dalam kes ini, vektor lajur didarab di sebelah kanan Ax, dan baris vektor berada di sebelah kiri x t A. Jika dimensi vektor J, dan dimensi matriks saya× J maka hasilnya akan menjadi vektor dimensi saya. Sebagai contoh,

nasi. 18 Mendarab vektor dengan matriks

Jika matriks A- segi empat sama ( saya× saya), kemudian vektor y = Ax mempunyai dimensi yang sama dengan x. Ia adalah jelas bahawa

A(α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Oleh itu, matriks boleh dianggap sebagai transformasi linear bagi vektor. khususnya Ix = x, lembu = 0 .

2. Maklumat tambahan

2.1. Sistem persamaan linear

biarlah A- saiz matriks saya× J, A b- vektor dimensi J. Pertimbangkan persamaan

Ax = b

berbanding dengan vektor x, dimensi saya. Pada asasnya, ia adalah satu sistem saya persamaan linear dengan J tidak diketahui x 1 ,...,x J. Penyelesaian wujud jika dan hanya jika

pangkat ( A) = pangkat( B) = R,

di mana B ialah matriks lanjutan dimensi saya×( J+1), terdiri daripada matriks A, ditambah dengan lajur b, B = (A b). Jika tidak, persamaan tidak konsisten.

Jika R = saya = J, maka penyelesaiannya adalah unik

x = A −1 b.

Jika R < saya, maka terdapat banyak penyelesaian berbeza yang boleh dinyatakan melalui gabungan linear J−R vektor. Sistem persamaan homogen Ax = 0 dengan matriks segi empat sama A (N× N) mempunyai penyelesaian bukan remeh ( x ≠ 0 ) jika dan hanya jika det( A) = 0. Jika R= pangkat( A)<N, maka ada N−R penyelesaian bebas linear.

2.2. Bentuk dwilinear dan kuadratik

Jika A ialah matriks segi empat sama, dan x Dan y- vektor dimensi yang sepadan, kemudian hasil darab skalar bentuk x t Ay dipanggil bilinear bentuk yang ditakrifkan oleh matriks A. Pada x = y ungkapan x t Ax dipanggil kuadratik bentuk.

2.3. Matriks pasti positif

Matriks segi empat sama A dipanggil pasti positif, jika untuk sebarang vektor bukan sifar x ≠ 0 ,

x t Ax > 0.

Ditakrifkan sama negatif (x t Ax < 0), bukan negatif (x t Ax≥ 0) dan negatif (x t Ax≤ 0) matriks tertentu.

2.4. Penguraian Cholesky

Jika matriks simetri A adalah pasti positif, maka terdapat matriks segi tiga yang unik U dengan unsur-unsur positif, yang mana

A = U t U.

Sebagai contoh,

nasi. 19 Penguraian Cholesky

2.5. Penguraian kutub

biarlah A ialah matriks segi empat sama bukan tunggal dimensi N× N. Kemudian ada yang unik polar prestasi

A = S.R.

di mana S ialah matriks simetri bukan negatif, dan R ialah matriks ortogon. Matriks S Dan R boleh ditakrifkan secara eksplisit:

S 2 = A.A. t atau S = (A.A. t) ½ dan R = S −1 A = (A.A. t) −½ A.

Sebagai contoh,

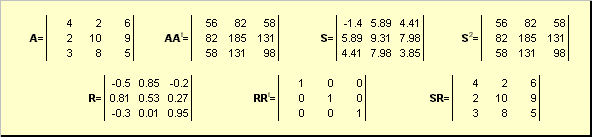
nasi. 20 Penguraian kutub

Jika matriks A adalah merosot, maka penguraian tidak unik - iaitu: S masih bersendirian, tetapi R mungkin banyak. Penguraian kutub mewakili matriks A sebagai gabungan mampatan/lanjutan S dan pusing R.

2.6. Vektor eigen dan nilai eigen

biarlah A ialah matriks segi empat sama. vektor v dipanggil eigenvector matriks A, Jika

Av = λ v,

di mana nombor λ dipanggil nilai eigen matriks A. Oleh itu, penjelmaan yang dilakukan oleh matriks A di atas vektor v, turun kepada regangan atau pemampatan mudah dengan pekali λ. Vektor eigen ditentukan sehingga pendaraban dengan pemalar α ≠ 0, i.e. Jika v ialah vektor eigen, kemudian α v- juga vektor eigen.

2.7. Nilai eigen

Di matriks A, dimensi ( N× N) tidak boleh lebih daripada N nilai eigen. Mereka berpuas hati persamaan ciri

det( A − λ saya) = 0,

yang merupakan persamaan algebra N-perintah ke-. Khususnya, untuk matriks 2×2 persamaan ciri mempunyai bentuk

Sebagai contoh,

nasi. 21 Nilai eigen

Set nilai eigen λ 1 ,..., λ N matriks A dipanggil spektrum A.

Spektrum mempunyai pelbagai sifat. khususnya

det( A) = λ 1 ×...×λ N,Sp( A) = λ 1 +...+λ N.

Nilai eigen bagi matriks arbitrari boleh menjadi nombor kompleks, tetapi jika matriks itu simetri ( A t = A), maka nilai eigennya adalah nyata.

2.8. Eigenvectors

Di matriks A, dimensi ( N× N) tidak boleh lebih daripada N eigenvectors, setiap satunya sepadan dengan nilai eigennya sendiri. Untuk menentukan vektor eigen v n perlu menyelesaikan sistem persamaan homogen

(A − λ n saya)v n = 0 .

Ia mempunyai penyelesaian yang tidak remeh, kerana det( A −λ n saya) = 0.

Sebagai contoh,

nasi. 22 Eigenvectors

Vektor eigen bagi matriks simetri adalah ortogon.