Een gelijktijdig systeem van lineaire vergelijkingen heeft een unieke oplossing. Methoden voor het oplossen van stelsels van lineaire vergelijkingen
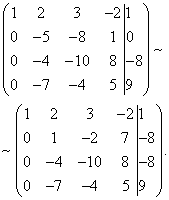
voorbeeld 1. Zoek een algemene oplossing en een specifieke oplossing van het systeemOplossing Wij doen het met behulp van een rekenmachine. Laten we de uitgebreide en hoofdmatrices opschrijven: 
De hoofdmatrix A wordt gescheiden door een stippellijn. We schrijven onbekende systemen bovenaan, waarbij we rekening houden met de mogelijke herschikking van termen in de vergelijkingen van het systeem. Door de rangorde van de uitgebreide matrix te bepalen, vinden we tegelijkertijd de rangorde van de belangrijkste. In matrix B zijn de eerste en tweede kolom proportioneel. Van de twee proportionele kolommen kan er maar één in de basismineur vallen, dus laten we bijvoorbeeld de eerste kolom voorbij de stippellijn met het tegenovergestelde teken verplaatsen. Voor het systeem betekent dit het overbrengen van termen van x 1 naar de rechterkant van de vergelijkingen. 
Laten we de matrix terugbrengen tot een driehoekige vorm. We zullen alleen met rijen werken, omdat het vermenigvuldigen van een matrixrij met een ander getal dan nul en het toevoegen ervan aan een andere rij voor het systeem betekent dat je de vergelijking met hetzelfde getal vermenigvuldigt en optelt met een andere vergelijking, wat de oplossing van de vergelijking niet verandert. systeem. We werken met de eerste rij: vermenigvuldig de eerste rij van de matrix met (-3) en voeg deze beurtelings toe aan de tweede en derde rij. Vermenigvuldig vervolgens de eerste regel met (-2) en tel deze op bij de vierde. 
De tweede en derde regel zijn proportioneel, daarom kan een ervan, bijvoorbeeld de tweede, worden doorgestreept. Dit komt overeen met het schrappen van de tweede vergelijking van het systeem, aangezien deze een gevolg is van de derde. 
Nu werken we met de tweede regel: vermenigvuldig deze met (-1) en tel deze op bij de derde. 
De minor omcirkeld met een stippellijn heeft de hoogste orde (van mogelijke minors) en is niet nul (hij is gelijk aan het product van de elementen op de hoofddiagonaal), en deze minor behoort daarom tot zowel de hoofdmatrix als de uitgebreide matrix. rangA = rangB = 3.
Minderjarige  is eenvoudig. Het bevat coëfficiënten voor de onbekenden x 2 , x 3 , x 4 , wat betekent dat de onbekenden x 2 , x 3 , x 4 afhankelijk zijn en x 1 , x 5 gratis zijn.
is eenvoudig. Het bevat coëfficiënten voor de onbekenden x 2 , x 3 , x 4 , wat betekent dat de onbekenden x 2 , x 3 , x 4 afhankelijk zijn en x 1 , x 5 gratis zijn.
Laten we de matrix transformeren, waarbij alleen de basismineur aan de linkerkant overblijft (wat overeenkomt met punt 4 van het bovenstaande oplossingsalgoritme). 
Het systeem met de coëfficiënten van deze matrix is gelijkwaardig aan het oorspronkelijke systeem en heeft de vorm

Met behulp van de methode voor het elimineren van onbekenden vinden we: ![]() , ,
, ,
We hebben relaties verkregen die de afhankelijke variabelen x 2, x 3, x 4 uitdrukken via de vrije x 1 en x 5, dat wil zeggen dat we een algemene oplossing hebben gevonden: 
Door waarden aan de vrije onbekenden toe te kennen, verkrijgen we een willekeurig aantal specifieke oplossingen. Laten we twee specifieke oplossingen vinden:
1) laat x 1 = x 5 = 0, dan x 2 = 1, x 3 = -3, x 4 = 3;
2) zet x 1 = 1, x 5 = -1, dan x 2 = 4, x 3 = -7, x 4 = 7.
Er werden dus twee oplossingen gevonden: (0,1,-3,3,0) – één oplossing, (1,4,-7,7,-1) – een andere oplossing.
Voorbeeld 2. Onderzoek de compatibiliteit, vind een algemene en een specifieke oplossing voor het systeem 
Oplossing. Laten we de eerste en tweede vergelijkingen herschikken zodat er één in de eerste vergelijking voorkomt en de matrix B schrijven. 
We krijgen nullen in de vierde kolom door met de eerste rij te werken: 
Nu krijgen we de nullen in de derde kolom met behulp van de tweede regel: 
 De derde en vierde regel zijn proportioneel, dus een ervan kan worden doorgestreept zonder de rangorde te veranderen:
De derde en vierde regel zijn proportioneel, dus een ervan kan worden doorgestreept zonder de rangorde te veranderen:
Vermenigvuldig de derde regel met (–2) en tel deze op bij de vierde: 
We zien dat de rangorde van de hoofd- en uitgebreide matrices gelijk is aan 4, en de rangorde valt samen met het aantal onbekenden, daarom heeft het systeem een unieke oplossing:
;
x 4 = 10- 3x 1 – 3x 2 – 2x 3 = 11.
Voorbeeld 3. Onderzoek het systeem op compatibiliteit en zoek een oplossing als deze bestaat. 
Oplossing. We stellen een uitgebreide matrix van het systeem samen. 
 We herschikken de eerste twee vergelijkingen zodat er 1 in de linkerbovenhoek staat:
We herschikken de eerste twee vergelijkingen zodat er 1 in de linkerbovenhoek staat:
Vermenigvuldig de eerste regel met (-1) en voeg deze toe aan de derde: 
Vermenigvuldig de tweede regel met (-2) en tel deze op bij de derde: 
Het systeem is inconsistent, omdat we in de hoofdmatrix een rij ontvingen die uit nullen bestond, die wordt doorgestreept wanneer de rangschikking wordt gevonden, maar in de uitgebreide matrix blijft de laatste rij bestaan, dat wil zeggen r B > r A .
Oefening. Onderzoek dit systeem van vergelijkingen op compatibiliteit en los het op met behulp van matrixrekening.
Oplossing
Voorbeeld. Bewijs de compatibiliteit van het systeem van lineaire vergelijkingen en los het op twee manieren op: 1) met de Gauss-methode; 2) Cramers methode. (voer het antwoord in de vorm in: x1,x2,x3)
Oplossing :doc :doc :xls
Antwoord: 2,-1,3.
Voorbeeld. Er wordt een systeem van lineaire vergelijkingen gegeven. Bewijs de compatibiliteit ervan. Zoek een algemene oplossing van het systeem en één specifieke oplossing.
Oplossing
Antwoord: x3 = - 1 + x4 + x5; x2 = 1 - x4; x 1 = 2 + x 4 - 3x 5
Oefening. Vind de algemene en specifieke oplossingen van elk systeem.
Oplossing. We bestuderen dit systeem met behulp van de stelling van Kronecker-Capelli.
Laten we de uitgebreide en hoofdmatrices opschrijven:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Hier is matrix A vetgedrukt weergegeven.
Laten we de matrix terugbrengen tot een driehoekige vorm. We zullen alleen met rijen werken, omdat het vermenigvuldigen van een matrixrij met een ander getal dan nul en het toevoegen ervan aan een andere rij voor het systeem betekent dat je de vergelijking met hetzelfde getal vermenigvuldigt en optelt met een andere vergelijking, wat de oplossing van de vergelijking niet verandert. systeem.
Laten we de eerste regel vermenigvuldigen met (3). Vermenigvuldig de tweede regel met (-1). Laten we de tweede regel aan de eerste toevoegen:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Laten we de tweede regel vermenigvuldigen met (2). Vermenigvuldig de derde regel met (-3). Laten we de derde regel aan de tweede toevoegen:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Vermenigvuldig de tweede regel met (-1). Laten we de tweede regel aan de eerste toevoegen:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
De geselecteerde minor heeft de hoogste orde (van mogelijke minoren) en is niet nul (het is gelijk aan het product van de elementen op de omgekeerde diagonaal), en deze minor behoort tot zowel de hoofdmatrix als de uitgebreide matrix, daarom rang( A) = rang(B) = 3 Omdat de rang van de hoofdmatrix gelijk is aan de rang van de uitgebreide matrix, dan het systeem is collaboratief.
Deze minor is eenvoudig. Het bevat coëfficiënten voor de onbekenden x 1 , x 2 , x 3 , wat betekent dat de onbekenden x 1 , x 2 , x 3 afhankelijk zijn (basis) en x 4 , x 5 gratis zijn.
Laten we de matrix transformeren, zodat alleen de basismineur aan de linkerkant overblijft.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
27x 3=
- x 2 + 13x 3 = - 1 + 3x 4 - 6x 5
2x 1 + 3x 2 - 3x 3 = 1 - 3x 4 + 2x 5
Met behulp van de methode voor het elimineren van onbekenden vinden we:
We hebben relaties verkregen die de afhankelijke variabelen x 1 , x 2 , x 3 uitdrukken via de vrije x 4 , x 5 , dat wil zeggen, we hebben gevonden gemeenschappelijk besluit:
x3 = 0
x 2 = 1 - 3x 4 + 6x 5
x 1 = - 1 + 3x 4 - 8x 5
onzeker, omdat heeft meer dan één oplossing.
Oefening. Los het stelsel vergelijkingen op.
Antwoord:x 2 = 2 - 1,67x 3 + 0,67x 4
x 1 = 5 - 3,67x 3 + 0,67x 4
Door waarden aan de vrije onbekenden toe te kennen, verkrijgen we een willekeurig aantal specifieke oplossingen. Het systeem is onzeker
Zoals duidelijk blijkt uit De stelling van Cramer Bij het oplossen van een stelsel lineaire vergelijkingen kunnen zich drie gevallen voordoen:
Eerste geval: een stelsel lineaire vergelijkingen heeft een unieke oplossing
(het systeem is consistent en definitief)
 Tweede geval: een stelsel lineaire vergelijkingen heeft een oneindig aantal oplossingen
Tweede geval: een stelsel lineaire vergelijkingen heeft een oneindig aantal oplossingen
(het systeem is consistent en onzeker)
** ![]() ,
,
die. de coëfficiënten van de onbekenden en de vrije termen zijn proportioneel.
 Derde geval: het stelsel lineaire vergelijkingen heeft geen oplossingen
Derde geval: het stelsel lineaire vergelijkingen heeft geen oplossingen
(het systeem is inconsistent)
Het systeem dus M lineaire vergelijkingen met N variabelen genoemd niet-gezamenlijk, als ze geen enkele oplossing heeft, en gewricht, als er minstens één oplossing is. Een gelijktijdig systeem van vergelijkingen dat slechts één oplossing heeft, wordt genoemd zeker, en meer dan één – onzeker.
Voorbeelden van het oplossen van stelsels van lineaire vergelijkingen met behulp van de Cramer-methode
Laat het systeem gegeven worden
 .
.
Gebaseerd op de stelling van Cramer
………….
,
Waar  -
-
systeembepalend. We verkrijgen de resterende determinanten door de kolom te vervangen door de coëfficiënten van de overeenkomstige variabele (onbekend) met vrije termen:



Voorbeeld 2.
 .
.

Het systeem is dus definitief. Om de oplossing te vinden, berekenen we de determinanten



Met behulp van de formules van Cramer vinden we:
![]()
Dus (1; 0; -1) is de enige oplossing voor het systeem.
Om de oplossingen van de stelsels van vergelijkingen 3 X 3 en 4 X 4 te controleren, kunt u een online rekenmachine gebruiken die de oplossingsmethode van Cramer gebruikt.
Als er in een systeem van lineaire vergelijkingen geen variabelen zijn in een of meer vergelijkingen, dan zijn in de determinant de overeenkomstige elementen gelijk aan nul! Dit is het volgende voorbeeld.
Voorbeeld 3. Los een stelsel lineaire vergelijkingen op met behulp van de Cramer-methode:
 .
.
Oplossing. We vinden de determinant van het systeem:

Kijk goed naar het stelsel vergelijkingen en naar de determinant van het systeem en herhaal het antwoord op de vraag in welke gevallen een of meer elementen van de determinant gelijk zijn aan nul. De determinant is dus niet gelijk aan nul en daarom is het systeem definitief. Om de oplossing te vinden, berekenen we de determinanten voor de onbekenden



Met behulp van de formules van Cramer vinden we:
De oplossing voor het systeem is dus (2; -1; 1).
6. Algemeen systeem van lineaire algebraïsche vergelijkingen. Gauss-methode.
Zoals we ons herinneren zijn de regel van Cramer en de matrixmethode ongeschikt in gevallen waarin het systeem oneindig veel oplossingen heeft of inconsistent is. Gauss-methode – het krachtigste en meest veelzijdige hulpmiddel voor het vinden van oplossingen voor elk systeem van lineaire vergelijkingen, welke in elk geval zal ons naar het antwoord leiden! Het methode-algoritme zelf werkt in alle drie de gevallen hetzelfde. Als de Cramer- en matrixmethoden kennis van determinanten vereisen, dan heb je voor het toepassen van de Gauss-methode alleen kennis van rekenkundige bewerkingen nodig, waardoor deze zelfs voor basisschoolleerlingen toegankelijk is.
Laten we eerst een beetje kennis over stelsels van lineaire vergelijkingen systematiseren. Een systeem van lineaire vergelijkingen kan:
1) Zorg voor een unieke oplossing.
2) Heb oneindig veel oplossingen.
3) Heb geen oplossingen (be niet-gezamenlijk).
De Gauss-methode is het krachtigste en meest universele hulpmiddel om een oplossing te vinden elk systemen van lineaire vergelijkingen. Zoals we ons herinneren, Regel en matrixmethode van Cramer zijn ongeschikt in gevallen waarin het systeem oneindig veel oplossingen heeft of inconsistent is. En de methode van opeenvolgende eliminatie van onbekenden Hoe dan ook zal ons naar het antwoord leiden! In deze les zullen we opnieuw de Gauss-methode bekijken voor geval nr. 1 (de enige oplossing voor het systeem), het artikel is gewijd aan de situaties van punten nr. 2-3. Ik merk op dat het algoritme van de methode zelf in alle drie de gevallen hetzelfde werkt.
Laten we terugkeren naar het eenvoudigste systeem uit de les Hoe los je een stelsel lineaire vergelijkingen op?
en los het op met behulp van de Gaussische methode.
De eerste stap is het opschrijven uitgebreide systeemmatrix:
. Ik denk dat iedereen kan zien volgens welk principe de coëfficiënten zijn geschreven. De verticale lijn binnen de matrix heeft geen enkele wiskundige betekenis; het is eenvoudigweg een doorhaling vanwege het ontwerpgemak.
Referentie:Ik raad je aan het te onthouden voorwaarden lineaire algebra. Systeemmatrix is een matrix die alleen bestaat uit coëfficiënten voor onbekenden, in dit voorbeeld de matrix van het systeem: . Uitgebreide systeemmatrix– dit is dezelfde matrix van het systeem plus een kolom met vrije termen, in dit geval: . Kortheidshalve kan elk van de matrices eenvoudigweg een matrix worden genoemd.
Nadat de uitgebreide systeemmatrix is geschreven, is het noodzakelijk om er enkele acties mee uit te voeren, die ook wel worden genoemd elementaire transformaties.
De volgende elementaire transformaties bestaan:
1) Snaren matrices kan worden herschikt in sommige plaatsen. In de betreffende matrix kunt u bijvoorbeeld pijnloos de eerste en tweede rij herschikken: 
2) Als er proportionele (in een speciaal geval identieke) rijen in de matrix zijn (of zijn verschenen), dan moet u verwijderen uit de matrix al deze rijen behalve één. Neem bijvoorbeeld de matrix  . In deze matrix zijn de laatste drie rijen proportioneel, dus het volstaat om er maar één over te laten:
. In deze matrix zijn de laatste drie rijen proportioneel, dus het volstaat om er maar één over te laten:  .
.
3) Als er tijdens transformaties een nulrij in de matrix verschijnt, dan zou dat ook zo moeten zijn verwijderen. Ik zal natuurlijk niet tekenen, de nullijn is de lijn waarin allemaal nullen.
4) De matrixrij kan zijn vermenigvuldigen (delen) naar welk nummer dan ook niet-nul. Neem bijvoorbeeld de matrix. Hier is het raadzaam om de eerste regel door –3 te delen en de tweede regel met 2 te vermenigvuldigen:  . Deze actie is erg handig omdat het verdere transformaties van de matrix vereenvoudigt.
. Deze actie is erg handig omdat het verdere transformaties van de matrix vereenvoudigt.
5) Deze transformatie veroorzaakt de meeste moeilijkheden, maar in feite is er ook niets ingewikkelds. Naar een rij van een matrix kan dat voeg nog een string toe, vermenigvuldigd met een getal, verschillend van nul. Laten we onze matrix bekijken vanuit een praktisch voorbeeld: . Eerst zal ik de transformatie gedetailleerd beschrijven. Vermenigvuldig de eerste regel met –2:  , En aan de tweede regel voegen we de eerste regel vermenigvuldigd met –2 toe:
, En aan de tweede regel voegen we de eerste regel vermenigvuldigd met –2 toe:  . Nu kan de eerste regel “terug” worden gedeeld door –2: . Zoals je kunt zien, is de regel TOEGEVOEGD LI – is niet veranderd. Altijd de regel WAARAAN WORDT TOEGEVOEGD verandert UT.
. Nu kan de eerste regel “terug” worden gedeeld door –2: . Zoals je kunt zien, is de regel TOEGEVOEGD LI – is niet veranderd. Altijd de regel WAARAAN WORDT TOEGEVOEGD verandert UT.
In de praktijk schrijven ze het natuurlijk niet zo gedetailleerd, maar schrijven ze het kort: 
Nogmaals: naar de tweede regel de eerste regel toegevoegd, vermenigvuldigd met –2. Een regel wordt meestal mondeling of op een schets vermenigvuldigd, waarbij het mentale rekenproces ongeveer als volgt gaat:
“Ik herschrijf de matrix en herschrijf de eerste regel:  »
»
“Eerste kolom. Onderaan moet ik nul krijgen. Daarom vermenigvuldig ik degene bovenaan met –2: , en tel ik de eerste op bij de tweede regel: 2 + (–2) = 0. Ik schrijf het resultaat op de tweede regel:  »
»
‘Nu de tweede kolom. Bovenaan vermenigvuldig ik -1 met -2: . Ik tel de eerste op bij de tweede regel: 1 + 2 = 3. Ik schrijf het resultaat in de tweede regel:  »
»
‘En de derde colonne. Bovenaan vermenigvuldig ik -5 met -2: . Ik tel de eerste op bij de tweede regel: –7 + 10 = 3. Ik schrijf het resultaat in de tweede regel:  »
»
Begrijp dit voorbeeld zorgvuldig en begrijp het sequentiële berekeningsalgoritme. Als je dit begrijpt, dan zit de Gaussische methode praktisch in je zak. Maar uiteraard blijven we aan deze transformatie werken.
Elementaire transformaties veranderen de oplossing van het stelsel vergelijkingen niet
! AANDACHT: overwogen manipulaties kan niet gebruiken, als u een taak wordt aangeboden waarbij de matrices ‘van zichzelf’ worden gegeven. Bijvoorbeeld met “klassiek” bewerkingen met matrixen Onder geen beding mag u iets binnen de matrices herschikken!
Laten we terugkeren naar ons systeem. Het wordt praktisch uit elkaar gehaald.
Laten we de uitgebreide matrix van het systeem opschrijven en deze met behulp van elementaire transformaties reduceren tot getrapte weergave:

(1) De eerste regel is opgeteld bij de tweede regel, vermenigvuldigd met –2. En nogmaals: waarom vermenigvuldigen we de eerste regel met –2? Om onderaan nul te krijgen, wat betekent dat je één variabele op de tweede regel moet verwijderen.
(2) Deel de tweede lijn door 3.
Het doel van elementaire transformaties –
reduceer de matrix tot een stapsgewijze vorm:  . Bij het ontwerp van de taak markeren ze eenvoudigweg de "trappen" met een eenvoudig potlood en omcirkelen ze ook de cijfers die zich op de "treden" bevinden. De term ‘stapsgewijze visie’ op zich is niet geheel theoretisch; in de wetenschappelijke en educatieve literatuur wordt hij vaak genoemd trapeziumvormige weergave of driehoekig aanzicht.
. Bij het ontwerp van de taak markeren ze eenvoudigweg de "trappen" met een eenvoudig potlood en omcirkelen ze ook de cijfers die zich op de "treden" bevinden. De term ‘stapsgewijze visie’ op zich is niet geheel theoretisch; in de wetenschappelijke en educatieve literatuur wordt hij vaak genoemd trapeziumvormige weergave of driehoekig aanzicht.
Als resultaat van elementaire transformaties hebben we verkregen equivalent origineel systeem van vergelijkingen:
Nu moet het systeem in de tegenovergestelde richting worden "afgewikkeld" - van onder naar boven wordt dit proces genoemd inverse van de Gaussische methode.
In de onderste vergelijking hebben we al een kant-en-klaar resultaat: .
Laten we de eerste vergelijking van het systeem bekijken en de reeds bekende waarde van “y” daarin vervangen:
Laten we eens kijken naar de meest voorkomende situatie, waarbij de Gaussische methode het oplossen van een systeem van drie lineaire vergelijkingen met drie onbekenden vereist.
voorbeeld 1
Los het stelsel vergelijkingen op met behulp van de Gauss-methode: 
Laten we de uitgebreide matrix van het systeem schrijven: 
Nu zal ik meteen het resultaat tekenen waar we tijdens de oplossing op zullen komen: 
En ik herhaal: ons doel is om de matrix naar een stapsgewijze vorm te brengen met behulp van elementaire transformaties. Waar te beginnen?
Kijk eerst naar het getal linksboven: 
Zou hier bijna altijd moeten zijn eenheid. Over het algemeen is –1 (en soms ook andere getallen) voldoende, maar op de een of andere manier is het van oudsher gebeurd dat er meestal één daar wordt geplaatst. Hoe organiseer je een eenheid? We kijken naar de eerste kolom - we hebben een voltooide eenheid! Transformatie één: verwissel de eerste en derde regel: 
Nu blijft de eerste regel ongewijzigd tot het einde van de oplossing. Nu prima.
De eenheid in de linkerbovenhoek is georganiseerd. Nu moet je op deze plaatsen nullen krijgen: 
We krijgen nullen met behulp van een “moeilijke” transformatie. Eerst behandelen we de tweede regel (2, –1, 3, 13). Wat moet er gebeuren om nul op de eerste positie te krijgen? Nodig hebben Voeg aan de tweede regel de eerste regel vermenigvuldigd met –2 toe. Vermenigvuldig de eerste regel mentaal of op een concept met –2: (–2, –4, 2, –18). En we voeren consequent (opnieuw mentaal of op basis van een concept) toevoeging uit, aan de tweede regel voegen we de eerste regel toe, al vermenigvuldigd met –2:
We schrijven het resultaat in de tweede regel: 
Op dezelfde manier gaan we om met de derde regel (3, 2, –5, –1). Om een nul in de eerste positie te krijgen, heb je nodig Voeg aan de derde regel de eerste regel vermenigvuldigd met –3 toe. Vermenigvuldig de eerste regel mentaal of op een concept met –3: (–3, –6, 3, –27). EN bij de derde regel voegen we de eerste regel vermenigvuldigd met –3 toe:
We schrijven het resultaat in de derde regel:
In de praktijk worden deze handelingen meestal mondeling uitgevoerd en in één stap opgeschreven: 
Het is niet nodig om alles in één keer en tegelijkertijd te tellen. De volgorde van berekeningen en het “inschrijven” van de resultaten consistent en meestal is het zo: eerst herschrijven we de eerste regel en blazen we langzaam op onszelf - CONSISTENT en AANDACHTIG:
En ik heb het mentale proces van de berekeningen zelf hierboven al besproken.
In dit voorbeeld is dit eenvoudig te doen; we delen de tweede regel door –5 (aangezien alle getallen daar deelbaar zijn door 5 zonder rest). Tegelijkertijd delen we de derde regel door –2, want hoe kleiner de getallen, hoe eenvoudiger de oplossing:
In de laatste fase van elementaire transformaties moet je hier nog een nul krijgen: 
Voor deze aan de derde regel voegen we de tweede regel vermenigvuldigd met –2 toe:
Probeer deze actie zelf uit te vinden - vermenigvuldig mentaal de tweede regel met –2 en voer de optelling uit.
De laatst uitgevoerde actie is het kapsel van het resultaat, deel de derde lijn door 3.
Als resultaat van elementaire transformaties werd een equivalent systeem van lineaire vergelijkingen verkregen: 
Koel.
Nu komt het omgekeerde van de Gaussische methode in het spel. De vergelijkingen ‘ontspannen’ van onder naar boven.
In de derde vergelijking hebben we al een kant-en-klaar resultaat:
Laten we naar de tweede vergelijking kijken: . De betekenis van "zet" is al bekend, dus:
En tenslotte de eerste vergelijking: . “Igrek” en “zet” zijn bekend, het is maar een kwestie van kleine dingen:
Antwoord: ![]()
Zoals al meerdere keren is opgemerkt, is het voor elk stelsel vergelijkingen mogelijk en noodzakelijk om de gevonden oplossing te controleren, gelukkig is dit gemakkelijk en snel.
Voorbeeld 2

Dit is een voorbeeld voor een onafhankelijke oplossing, een voorbeeld van het definitieve ontwerp en een antwoord aan het einde van de les.
Opgemerkt moet worden dat uw voortgang van de beslissing valt misschien niet samen met mijn besluitvormingsproces, en dit is een kenmerk van de Gauss-methode. Maar de antwoorden moeten hetzelfde zijn!
Voorbeeld 3
Los een stelsel lineaire vergelijkingen op met behulp van de Gauss-methode 
Laten we de uitgebreide matrix van het systeem opschrijven en deze, met behulp van elementaire transformaties, in een stapsgewijze vorm brengen:
We kijken naar de “stap” linksboven. We zouden er daar een moeten hebben. Het probleem is dat er helemaal geen eenheden in de eerste kolom staan, dus het herschikken van de rijen zal niets oplossen. In dergelijke gevallen moet de eenheid worden georganiseerd met behulp van een elementaire transformatie. Dit kan meestal op verschillende manieren. Ik heb dit gedaan:
(1) Aan de eerste regel voegen we de tweede regel toe, vermenigvuldigd met –1. Dat wil zeggen, we hebben de tweede regel mentaal met –1 vermenigvuldigd en de eerste en tweede regel bij elkaar opgeteld, terwijl de tweede regel niet veranderde.

Linksboven staat nu “min één”, wat ons best goed uitkomt. Iedereen die +1 wil krijgen, kan een extra beweging uitvoeren: vermenigvuldig de eerste regel met –1 (verander het teken).
(2) De eerste regel vermenigvuldigd met 5 werd toegevoegd aan de tweede regel. De eerste regel vermenigvuldigd met 3 werd toegevoegd aan de derde regel.
(3) De eerste regel is vermenigvuldigd met –1, in principe is dit voor schoonheid. Het teken van de derde regel werd ook veranderd en verplaatst naar de tweede plaats, zodat we bij de tweede “stap” de vereiste eenheid hadden.
(4) De tweede regel werd opgeteld bij de derde regel, vermenigvuldigd met 2.
(5) De derde regel werd gedeeld door 3.
Een slecht teken dat duidt op een fout in de berekeningen (zelden een typefout) is een ‘slechte’ bedrijfsresultaten. Dat wil zeggen, als we iets als , hieronder krijgen, en dienovereenkomstig, ![]() , dan kunnen we met een hoge mate van waarschijnlijkheid zeggen dat er een fout is gemaakt tijdens elementaire transformaties.
, dan kunnen we met een hoge mate van waarschijnlijkheid zeggen dat er een fout is gemaakt tijdens elementaire transformaties.
Wij hanteren het omgekeerde: bij het ontwerpen van voorbeelden herschrijven ze vaak niet het systeem zelf, maar worden de vergelijkingen ‘rechtstreeks uit de gegeven matrix gehaald’. Ik herinner u eraan dat de omgekeerde slag van onder naar boven werkt. Ja, hier is een cadeau:
Antwoord: ![]() .
.
Voorbeeld 4
Los een stelsel lineaire vergelijkingen op met behulp van de Gauss-methode 
Dit is een voorbeeld dat u zelf kunt oplossen, het is iets ingewikkelder. Het is oké als iemand in de war raakt. Volledige oplossing en voorbeeldontwerp aan het einde van de les. Jouw oplossing kan afwijken van mijn oplossing.
In het laatste deel zullen we enkele kenmerken van het Gauss-algoritme bekijken.
Het eerste kenmerk is dat sommige variabelen soms ontbreken in de systeemvergelijkingen, bijvoorbeeld: 
Hoe schrijf ik de uitgebreide systeemmatrix correct? Ik heb dit punt al besproken in de klas. De regel van Cramer. Matrix-methode. In de uitgebreide matrix van het systeem plaatsen we nullen in plaats van ontbrekende variabelen: 
Dit is overigens een vrij eenvoudig voorbeeld, aangezien de eerste kolom al één nul heeft en er minder elementaire transformaties hoeven te worden uitgevoerd.
Het tweede kenmerk is dit. In alle beschouwde voorbeelden hebben we –1 of +1 op de “stappen” geplaatst. Zouden er nog andere cijfers kunnen zijn? In sommige gevallen kunnen ze dat wel. Beschouw het systeem:  .
.
Hier linksboven “stap” hebben we een twee. Maar het valt ons op dat alle getallen in de eerste kolom deelbaar zijn door 2 zonder rest - en de andere is twee en zes. En de twee linksboven passen bij ons! In de eerste stap moet u de volgende transformaties uitvoeren: tel de eerste regel vermenigvuldigd met –1 op bij de tweede regel; Voeg aan de derde regel de eerste regel vermenigvuldigd met –3 toe. Op deze manier krijgen we de vereiste nullen in de eerste kolom.
Of een ander conventioneel voorbeeld:  . Hier passen de drie op de tweede “stap” ook bij ons, aangezien 12 (de plaats waar we nul moeten krijgen) deelbaar is door 3 zonder rest. Het is noodzakelijk om de volgende transformatie uit te voeren: voeg de tweede regel toe aan de derde regel, vermenigvuldigd met –4, waardoor de nul wordt verkregen die we nodig hebben.
. Hier passen de drie op de tweede “stap” ook bij ons, aangezien 12 (de plaats waar we nul moeten krijgen) deelbaar is door 3 zonder rest. Het is noodzakelijk om de volgende transformatie uit te voeren: voeg de tweede regel toe aan de derde regel, vermenigvuldigd met –4, waardoor de nul wordt verkregen die we nodig hebben.
De methode van Gauss is universeel, maar er is één bijzonderheid. Je kunt vol vertrouwen systemen leren oplossen met behulp van andere methoden (Cramer's methode, matrixmethode), letterlijk de eerste keer - ze hebben een zeer strikt algoritme. Maar om vertrouwen te hebben in de Gauss-methode, moet je er goed in worden en minstens 5-10 systemen oplossen. Daarom kunnen er in eerste instantie verwarring en fouten in de berekeningen optreden, en daar is niets ongewoons of tragisch aan.
Regenachtig herfstweer buiten het raam.... Daarom voor iedereen die een complexer voorbeeld zelf wil oplossen:
Voorbeeld 5
Los een stelsel van vier lineaire vergelijkingen met vier onbekenden op met behulp van de Gauss-methode. 
Een dergelijke taak is in de praktijk niet zo zeldzaam. Ik denk dat zelfs een theepot die deze pagina grondig heeft bestudeerd het algoritme voor het intuïtief oplossen van een dergelijk systeem zal begrijpen. In wezen is alles hetzelfde: er zijn alleen meer acties.
Gevallen waarin het systeem geen oplossingen heeft (inconsistent) of oneindig veel oplossingen heeft, worden in de les besproken Incompatibele systemen en systemen met een gemeenschappelijke oplossing. Daar kunt u het overwogen algoritme van de Gauss-methode repareren.
Ik wens je succes!
Oplossingen en antwoorden:
Voorbeeld 2: Oplossing: Laten we de uitgebreide matrix van het systeem opschrijven en deze, met behulp van elementaire transformaties, in een stapsgewijze vorm brengen.

Elementaire transformaties uitgevoerd:
(1) De eerste regel is opgeteld bij de tweede regel, vermenigvuldigd met –2. De eerste regel werd opgeteld bij de derde regel, vermenigvuldigd met –1. Aandacht! Hier kunt u in de verleiding komen om de eerste van de derde regel af te trekken; ik raad u ten zeerste aan deze niet af te trekken - het risico op fouten neemt aanzienlijk toe. Vouw het gewoon!
(2) Het teken van de tweede regel is gewijzigd (vermenigvuldigd met –1). De tweede en derde regel zijn verwisseld. opmerking, dat we op de “stappen” niet alleen tevreden zijn met één, maar ook met –1, wat nog handiger is.
(3) De tweede regel is toegevoegd aan de derde regel, vermenigvuldigd met 5.
(4) Het teken van de tweede regel is gewijzigd (vermenigvuldigd met –1). De derde lijn werd gedeeld door 14.
Achteruit:
Antwoord: ![]() .
.
Voorbeeld 4: Oplossing: Laten we de uitgebreide matrix van het systeem opschrijven en deze, met behulp van elementaire transformaties, in een stapsgewijze vorm brengen:

Uitgevoerde conversies:
(1) Er is een tweede regel toegevoegd aan de eerste regel. De gewenste eenheid is dus georganiseerd in de “stap” linksboven.
(2) De eerste regel vermenigvuldigd met 7 werd toegevoegd aan de tweede regel. De eerste regel vermenigvuldigd met 6 werd toegevoegd aan de derde regel.
Met de tweede “stap” wordt alles erger, de “kandidaten” ervoor zijn de nummers 17 en 23, en we hebben één of –1 nodig. Transformaties (3) en (4) zullen gericht zijn op het verkrijgen van de gewenste eenheid
(3) De tweede regel werd opgeteld bij de derde regel, vermenigvuldigd met –1.
(4) De derde regel werd opgeteld bij de tweede regel, vermenigvuldigd met –3.
Het vereiste item in de tweede stap is ontvangen.
.
(5) De tweede regel werd opgeteld bij de derde regel, vermenigvuldigd met 6.
Als onderdeel van de lessen Gaussische methode En Incompatibele systemen/systemen met een gemeenschappelijke oplossing wij hebben overwogen inhomogene systemen van lineaire vergelijkingen, Waar gratis lid(meestal rechts) minstens een uit de vergelijkingen verschilde van nul.
En nu, na een goede warming-up met matrix rang, we blijven de techniek oppoetsen elementaire transformaties op homogeen systeem van lineaire vergelijkingen.
Op basis van de eerste alinea's lijkt het materiaal misschien saai en middelmatig, maar deze indruk is bedrieglijk. Naast de verdere ontwikkeling van technieken zal er veel nieuwe informatie zijn, dus probeer de voorbeelden in dit artikel niet te negeren.
De Gaussische methode, ook wel de methode voor de sequentiële eliminatie van onbekenden genoemd, is als volgt. Met behulp van elementaire transformaties wordt een systeem van lineaire vergelijkingen in een zodanige vorm gebracht dat de matrix van coëfficiënten dat blijkt te zijn trapeziumvormig (hetzelfde als driehoekig of getrapt) of bijna trapeziumvormig (directe slag van de Gauss-methode, hierna eenvoudigweg rechte slag). Een voorbeeld van een dergelijk systeem en de oplossing ervan vindt u in de bovenstaande figuur.
In een dergelijk systeem bevat de laatste vergelijking slechts één variabele en kan de waarde ervan ondubbelzinnig worden gevonden. De waarde van deze variabele wordt vervolgens vervangen door de vorige vergelijking ( inverse van de Gaussische methode , dan precies andersom), waaruit de vorige variabele wordt gevonden, enzovoort.
In een trapeziumvormig (driehoekig) systeem bevat de derde vergelijking, zoals we zien, geen variabelen meer j En X, en de tweede vergelijking is de variabele X .
Nadat de matrix van het systeem een trapeziumvormige vorm heeft aangenomen, is het niet langer moeilijk om de kwestie van de compatibiliteit van het systeem te begrijpen, het aantal oplossingen te bepalen en de oplossingen zelf te vinden.
Voordelen van de methode:
- bij het oplossen van stelsels lineaire vergelijkingen met meer dan drie vergelijkingen en onbekenden is de Gauss-methode niet zo omslachtig als de Cramer-methode, aangezien het oplossen met de Gauss-methode minder berekeningen vereist;
- de Gauss-methode kan onbepaalde stelsels van lineaire vergelijkingen oplossen, dat wil zeggen, ze hebben een algemene oplossing (en we zullen ze in deze les analyseren), en met behulp van de Cramer-methode kunnen we alleen maar stellen dat het systeem onbepaald is;
- je kunt stelsels lineaire vergelijkingen oplossen waarin het aantal onbekenden niet gelijk is aan het aantal vergelijkingen (we zullen ze in deze les ook analyseren);
- De methode is gebaseerd op elementaire (school)methoden - de methode voor het vervangen van onbekenden en de methode voor het toevoegen van vergelijkingen, die we in het overeenkomstige artikel hebben besproken.
Om iedereen de eenvoud te laten begrijpen waarmee trapeziumvormige (driehoekige, stapvormige) systemen van lineaire vergelijkingen worden opgelost, presenteren we een oplossing voor een dergelijk systeem met behulp van omgekeerde beweging. Een snelle oplossing voor dit systeem werd aan het begin van de les op de afbeelding getoond.
Voorbeeld 1. Los een stelsel lineaire vergelijkingen op met inverse:
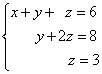
Oplossing. In dit trapeziumvormige systeem is de variabele z kan op unieke wijze worden gevonden uit de derde vergelijking. We vervangen de waarde ervan in de tweede vergelijking en krijgen de waarde van de variabele j:
Nu kennen we de waarden van twee variabelen - z En j. We vervangen ze in de eerste vergelijking en krijgen de waarde van de variabele X:
Uit de voorgaande stappen schrijven we de oplossing van het stelsel vergelijkingen op:
![]()
Om zo'n trapeziumvormig systeem van lineaire vergelijkingen te verkrijgen, dat we heel eenvoudig hebben opgelost, is het noodzakelijk om een voorwaartse slag te gebruiken die verband houdt met elementaire transformaties van het systeem van lineaire vergelijkingen. Het is ook niet heel moeilijk.
Elementaire transformaties van een systeem van lineaire vergelijkingen
Door de schoolmethode van het algebraïsch optellen van de vergelijkingen van een systeem te herhalen, kwamen we erachter dat we aan een van de vergelijkingen van het systeem een andere vergelijking van het systeem kunnen toevoegen, en elk van de vergelijkingen kan met een aantal getallen worden vermenigvuldigd. Als resultaat verkrijgen we een stelsel van lineaire vergelijkingen dat gelijkwaardig is aan dit systeem. Daarin bevatte één vergelijking al slechts één variabele, door de waarde ervan in andere vergelijkingen te vervangen, komen we tot een oplossing. Een dergelijke toevoeging is een van de soorten elementaire transformatie van het systeem. Wanneer we de Gaussische methode gebruiken, kunnen we verschillende soorten transformaties gebruiken.

De animatie hierboven laat zien hoe het stelsel vergelijkingen geleidelijk verandert in een trapeziumvormig systeem. Dat wil zeggen degene die je in de allereerste animatie zag en jezelf ervan overtuigde dat het gemakkelijk is om de waarden van alle onbekenden daaruit te vinden. Hoe een dergelijke transformatie moet worden uitgevoerd en uiteraard voorbeelden zullen verder worden besproken.
Bij het oplossen van stelsels van lineaire vergelijkingen met een willekeurig aantal vergelijkingen en onbekenden in het stelsel van vergelijkingen en in de uitgebreide matrix van het systeem Kan:
- herschik de regels (dit werd helemaal aan het begin van dit artikel vermeld);
- als andere transformaties resulteren in gelijke of proportionele rijen, kunnen ze worden verwijderd, op één na;
- verwijder “nul”-rijen waar alle coëfficiënten gelijk zijn aan nul;
- vermenigvuldig of deel een tekenreeks met een bepaald getal;
- voeg aan elke regel nog een regel toe, vermenigvuldigd met een bepaald getal.
Als resultaat van de transformaties verkrijgen we een stelsel van lineaire vergelijkingen dat gelijkwaardig is aan dit systeem.
Algoritme en voorbeelden van het oplossen van een systeem van lineaire vergelijkingen met een vierkante matrix van het systeem met behulp van de Gauss-methode
Laten we eerst eens kijken naar het oplossen van stelsels van lineaire vergelijkingen waarin het aantal onbekenden gelijk is aan het aantal vergelijkingen. De matrix van een dergelijk systeem is vierkant, dat wil zeggen dat het aantal rijen daarin gelijk is aan het aantal kolommen.
Voorbeeld 2. Los een stelsel lineaire vergelijkingen op met behulp van de Gauss-methode
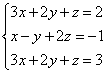
Bij het oplossen van systemen van lineaire vergelijkingen met behulp van schoolmethoden, vermenigvuldigden we een van de vergelijkingen term voor term met een bepaald getal, zodat de coëfficiënten van de eerste variabele in de twee vergelijkingen tegengestelde getallen waren. Bij het toevoegen van vergelijkingen wordt deze variabele geëlimineerd. De Gauss-methode werkt op dezelfde manier.
Om het uiterlijk van de oplossing te vereenvoudigen laten we een uitgebreide matrix van het systeem maken:

In deze matrix bevinden de coëfficiënten van de onbekenden zich links vóór de verticale lijn, en de vrije termen bevinden zich rechts na de verticale lijn.
Voor het gemak van deelcoëfficiënten voor variabelen (om deling door eenheid te verkrijgen) Laten we de eerste en tweede rij van de systeemmatrix omwisselen. We verkrijgen een systeem dat gelijkwaardig is aan dit systeem, omdat in een systeem van lineaire vergelijkingen de vergelijkingen kunnen worden uitgewisseld:

Met behulp van de nieuwe eerste vergelijking elimineer de variabele X uit de tweede en alle daaropvolgende vergelijkingen. Om dit te doen, voegen we aan de tweede rij van de matrix de eerste rij vermenigvuldigd met (in ons geval met ) toe aan de derde rij - de eerste rij vermenigvuldigd met (in ons geval met ).
Dit is mogelijk omdat
Als er meer dan drie vergelijkingen in ons systeem zouden zijn, zouden we aan alle volgende vergelijkingen de eerste regel moeten toevoegen, vermenigvuldigd met de verhouding van de overeenkomstige coëfficiënten, genomen met een minteken.
Als resultaat verkrijgen we een matrix die equivalent is aan dit systeem van een nieuw systeem van vergelijkingen, waarin alle vergelijkingen, beginnend bij de tweede bevatten geen variabele X :
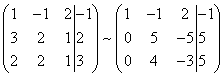
Om de tweede regel van het resulterende systeem te vereenvoudigen, vermenigvuldigt u deze met en verkrijgt u opnieuw de matrix van een stelsel vergelijkingen dat equivalent is aan dit systeem:

Als we nu de eerste vergelijking van het resulterende systeem ongewijzigd laten, met behulp van de tweede vergelijking elimineren we de variabele j uit alle volgende vergelijkingen. Om dit te doen, voegen we aan de derde rij van de systeemmatrix de tweede rij toe, vermenigvuldigd met (in ons geval met ).
Als er meer dan drie vergelijkingen in ons systeem zouden zijn, zouden we een tweede regel moeten toevoegen aan alle volgende vergelijkingen, vermenigvuldigd met de verhouding van de overeenkomstige coëfficiënten, genomen met een minteken.
Als resultaat verkrijgen we opnieuw de matrix van een systeem dat equivalent is aan dit systeem van lineaire vergelijkingen:
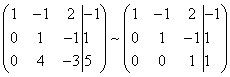
We hebben een equivalent trapeziumvormig systeem van lineaire vergelijkingen verkregen:

Als het aantal vergelijkingen en variabelen groter is dan in ons voorbeeld, gaat het proces van het opeenvolgend elimineren van variabelen door totdat de systeemmatrix trapeziumvormig wordt, zoals in ons demovoorbeeld.
We zullen de oplossing “vanaf het einde” vinden: de omgekeerde beweging. Voor deze uit de laatste vergelijking die we bepalen z:
.
Door deze waarde in de vorige vergelijking te vervangen, wij zullen vinden j:
Vanaf de eerste vergelijking wij zullen vinden X:
![]()
Antwoord: de oplossing voor dit stelsel vergelijkingen is: ![]() .
.
: in dit geval wordt hetzelfde antwoord gegeven als het systeem een unieke oplossing heeft. Als het systeem een oneindig aantal oplossingen heeft, dan is dit het antwoord, en dit is het onderwerp van het vijfde deel van deze les.
Los zelf een stelsel lineaire vergelijkingen op met behulp van de Gauss-methode en kijk vervolgens naar de oplossing
Hier hebben we opnieuw een voorbeeld van een consistent en definitief systeem van lineaire vergelijkingen, waarin het aantal vergelijkingen gelijk is aan het aantal onbekenden. Het verschil met ons demovoorbeeld van het algoritme is dat er al vier vergelijkingen en vier onbekenden zijn.
Voorbeeld 4. Los een stelsel lineaire vergelijkingen op met behulp van de Gauss-methode:


Nu moet je de tweede vergelijking gebruiken om de variabele uit volgende vergelijkingen te verwijderen. Laten we het voorbereidende werk uitvoeren. Om het handiger te maken met de verhouding van coëfficiënten, moet je er een in de tweede kolom van de tweede rij krijgen. Om dit te doen, trekt u de derde van de tweede regel af en vermenigvuldigt u de resulterende tweede regel met -1.
Laten we nu de daadwerkelijke eliminatie van de variabele uit de derde en vierde vergelijking uitvoeren. Om dit te doen, voegt u de tweede regel, vermenigvuldigd met , toe aan de derde regel, en de tweede, vermenigvuldigd met , aan de vierde regel.

Met behulp van de derde vergelijking elimineren we nu de variabele uit de vierde vergelijking. Om dit te doen, voegt u de derde regel toe aan de vierde regel, vermenigvuldigd met . We verkrijgen een uitgebreide trapeziumvormige matrix.

We hebben een stelsel vergelijkingen verkregen waaraan het gegeven systeem equivalent is:

Bijgevolg zijn de resulterende en gegeven systemen compatibel en definitief. We vinden de uiteindelijke oplossing ‘vanaf het einde’. Uit de vierde vergelijking kunnen we rechtstreeks de waarde van de variabele “x-vier” uitdrukken:
We substitueren deze waarde in de derde vergelijking van het systeem en krijgen
![]() ,
,
![]() ,
,
Tenslotte: waardevervanging
De eerste vergelijking geeft
![]() ,
,
waar vinden we “x eerst”:
Antwoord: dit stelsel vergelijkingen heeft een unieke oplossing ![]() .
.
Je kunt de oplossing van het systeem ook op een rekenmachine controleren met behulp van de methode van Cramer: in dit geval wordt hetzelfde antwoord gegeven als het systeem een unieke oplossing heeft.
Het oplossen van toegepaste problemen met behulp van de Gauss-methode aan de hand van het voorbeeld van een probleem met legeringen
Systemen van lineaire vergelijkingen worden gebruikt om echte objecten in de fysieke wereld te modelleren. Laten we een van deze problemen oplossen: legeringen. Soortgelijke problemen zijn problemen met mengsels, de kosten of het aandeel van individuele goederen in een groep goederen, en dergelijke.
Voorbeeld 5. Drie stukken legering hebben een totale massa van 150 kg. De eerste legering bevat 60% koper, de tweede - 30%, de derde - 10%. Bovendien is er in de tweede en derde legering samen 28,4 kg minder koper dan in de eerste legering, en in de derde legering 6,2 kg minder koper dan in de tweede. Zoek de massa van elk stuk van de legering.
Oplossing. We stellen een systeem van lineaire vergelijkingen samen:

We vermenigvuldigen de tweede en derde vergelijking met 10, we verkrijgen een equivalent systeem van lineaire vergelijkingen:
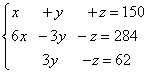
We creëren een uitgebreide matrix van het systeem:

Let op, rechtdoor. Door één rij op te tellen (in ons geval afgetrokken) vermenigvuldigd met een getal (we passen dit twee keer toe), vinden de volgende transformaties plaats met de uitgebreide matrix van het systeem:

De directe verhuizing is voorbij. We verkregen een uitgebreide trapeziumvormige matrix.
We passen de omgekeerde beweging toe. Wij vinden de oplossing vanaf het einde. We zien dat.
Uit de tweede vergelijking vinden we
Uit de derde vergelijking -
Je kunt de oplossing van het systeem ook op een rekenmachine controleren met behulp van de methode van Cramer: in dit geval wordt hetzelfde antwoord gegeven als het systeem een unieke oplossing heeft.
De eenvoud van de methode van Gauss blijkt uit het feit dat de Duitse wiskundige Carl Friedrich Gauss slechts 15 minuten nodig had om deze uit te vinden. Naast de naar hem genoemde methode is het gezegde "We moeten wat ons ongelooflijk en onnatuurlijk lijkt niet te verwarren met het absoluut onmogelijke" bekend uit de werken van Gauss - een soort korte instructie over het doen van ontdekkingen.
Bij veel toegepaste problemen is er misschien geen derde beperking, dat wil zeggen een derde vergelijking, dan moet je een stelsel van twee vergelijkingen met drie onbekenden oplossen met behulp van de Gaussiaanse methode, of, omgekeerd, er zijn minder onbekenden dan vergelijkingen. We zullen nu beginnen met het oplossen van dergelijke stelsels vergelijkingen.
Met behulp van de Gauss-methode kunt u bepalen of een systeem compatibel of incompatibel is N lineaire vergelijkingen met N variabelen.
De Gauss-methode en systemen van lineaire vergelijkingen met een oneindig aantal oplossingen
Het volgende voorbeeld is een consistent maar onbepaald systeem van lineaire vergelijkingen, dat wil zeggen met een oneindig aantal oplossingen.
Na het uitvoeren van transformaties in de uitgebreide matrix van het systeem (rijen herschikken, rijen vermenigvuldigen en delen door een bepaald getal, een andere toevoegen aan een rij), kunnen rijen van het formulier verschijnen
Als in alle vergelijkingen de vorm
Vrije termen zijn gelijk aan nul, dit betekent dat het systeem onbepaald is, dat wil zeggen dat het een oneindig aantal oplossingen heeft, en vergelijkingen van dit type zijn "overbodig" en we sluiten ze uit van het systeem.
Voorbeeld 6.
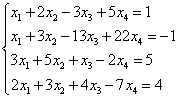
Oplossing. Laten we een uitgebreide matrix van het systeem maken. Vervolgens elimineren we met behulp van de eerste vergelijking de variabele uit volgende vergelijkingen. Om dit te doen, voegt u aan de tweede, derde en vierde regel de eerste toe, vermenigvuldigd met:

Laten we nu de tweede regel toevoegen aan de derde en vierde.

Zo komen we bij het systeem terecht

De laatste twee vergelijkingen zijn omgezet in vergelijkingen van de vorm. Aan deze vergelijkingen wordt voldaan voor elke waarde van de onbekenden en kunnen worden weggegooid.
Om aan de tweede vergelijking te voldoen, kunnen we willekeurige waarden kiezen voor en , waarna de waarde voor uniek wordt bepaald: ![]() . Uit de eerste vergelijking wordt de waarde voor ook uniek gevonden:
. Uit de eerste vergelijking wordt de waarde voor ook uniek gevonden: ![]() .
.
Zowel het gegeven als het laatste systeem zijn consistent, maar onzeker, evenals de formules
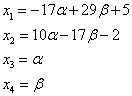
voor willekeurig en geef ons alle oplossingen van een bepaald systeem.
Gauss-methode en systemen van lineaire vergelijkingen zonder oplossingen
Het volgende voorbeeld is een inconsistent stelsel van lineaire vergelijkingen, dat wil zeggen een stelsel dat geen oplossingen heeft. Het antwoord op dergelijke problemen wordt als volgt geformuleerd: het systeem heeft geen oplossingen.
Zoals reeds vermeld in verband met het eerste voorbeeld, kunnen na het uitvoeren van transformaties rijen van het formulier verschijnen in de uitgebreide matrix van het systeem
overeenkomend met een vergelijking van de vorm
Als er onder hen minstens één vergelijking is met een vrije term die niet nul is (d.w.z. ), dan is dit systeem van vergelijkingen inconsistent, dat wil zeggen dat het geen oplossingen heeft en dat de oplossing compleet is.
Voorbeeld 7. Los het stelsel van lineaire vergelijkingen op met behulp van de Gauss-methode:

Oplossing. We stellen een uitgebreide matrix van het systeem samen. Met behulp van de eerste vergelijking sluiten we de variabele uit van volgende vergelijkingen. Om dit te doen, voegt u de eerste regel vermenigvuldigd met toe aan de tweede regel, de eerste regel vermenigvuldigd met de derde regel en de eerste regel vermenigvuldigd met de vierde regel.

Nu moet je de tweede vergelijking gebruiken om de variabele uit volgende vergelijkingen te verwijderen. Om geheeltallige verhoudingen van coëfficiënten te verkrijgen, verwisselen we de tweede en derde rij van de uitgebreide matrix van het systeem.

Om de derde en vierde vergelijking uit te sluiten, voegt u de tweede vermenigvuldigd met , toe aan de derde regel, en de tweede vermenigvuldigd met , aan de vierde regel.
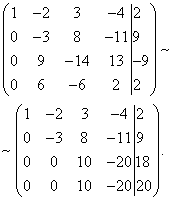
Met behulp van de derde vergelijking elimineren we nu de variabele uit de vierde vergelijking. Om dit te doen, voegt u de derde regel toe aan de vierde regel, vermenigvuldigd met .

Het gegeven systeem is daarom gelijkwaardig aan het volgende:

Het resulterende systeem is inconsistent, omdat aan de laatste vergelijking niet kan worden voldaan door welke waarden van de onbekenden dan ook. Daarom heeft dit systeem geen oplossingen.
In deze les zullen we kijken naar methoden voor het oplossen van een stelsel lineaire vergelijkingen. In een cursus hogere wiskunde moeten systemen van lineaire vergelijkingen worden opgelost, zowel in de vorm van afzonderlijke taken, bijvoorbeeld 'Los het systeem op met behulp van de formules van Cramer', als tijdens het oplossen van andere problemen. Systemen van lineaire vergelijkingen komen in bijna alle takken van de hogere wiskunde aan bod.
Eerst een beetje theorie. Wat betekent het wiskundige woord ‘lineair’ in dit geval? Dit betekent dat de vergelijkingen van het systeem Alle variabelen inbegrepen in de eerste graad: zonder fancy dingen zoals ![]() enz., waar alleen deelnemers aan wiskundige olympiades blij mee zijn.
enz., waar alleen deelnemers aan wiskundige olympiades blij mee zijn.
In de hogere wiskunde worden niet alleen letters uit de kindertijd gebruikt om variabelen aan te duiden.
Een redelijk populaire optie zijn variabelen met indexen: .
Of de beginletters van het Latijnse alfabet, klein en groot:
Het is niet zo zeldzaam om Griekse letters te vinden: – bij velen bekend als “alpha, beta, gamma”. En ook een setje met indexen van bijvoorbeeld de letter “mu”:
Het gebruik van een of andere reeks letters hangt af van het deel van de hogere wiskunde waarin we worden geconfronteerd met een systeem van lineaire vergelijkingen. In stelsels van lineaire vergelijkingen die je bijvoorbeeld tegenkomt bij het oplossen van integralen en differentiaalvergelijkingen, is het traditioneel om de notatie te gebruiken
Maar hoe de variabelen ook worden aangeduid, de principes, methoden en methoden voor het oplossen van een systeem van lineaire vergelijkingen veranderen niet. Dus als je iets engs tegenkomt, zoals , haast je dan niet om het probleemboek uit angst te sluiten. Je kunt immers in plaats daarvan de zon tekenen, in plaats daarvan een vogel en in plaats daarvan een gezicht (de leraar). En hoe grappig het ook mag lijken, een systeem van lineaire vergelijkingen met deze notaties kan ook worden opgelost.
Ik heb het gevoel dat het artikel behoorlijk lang zal worden, dus een kleine inhoudsopgave. De opeenvolgende “debriefing” zal er dus als volgt uitzien:
– Een stelsel van lineaire vergelijkingen oplossen met behulp van de substitutiemethode (“schoolmethode”);
– Het systeem oplossen door de systeemvergelijkingen term voor term op te tellen (aftrekken).;
– Oplossing van het systeem met behulp van de formules van Cramer;
– Het systeem oplossen met behulp van een inverse matrix;
– Het systeem oplossen met behulp van de Gaussiaanse methode.
Iedereen kent systemen van lineaire vergelijkingen uit wiskundecursussen op school. Eigenlijk beginnen we met herhaling.
Een stelsel van lineaire vergelijkingen oplossen met behulp van de substitutiemethode
Deze methode wordt ook wel de “schoolmethode” genoemd, of de methode om onbekenden te elimineren. Figuurlijk gesproken kan het ook ‘een onvoltooide Gaussiaanse methode’ worden genoemd.
voorbeeld 1
![]()
Hier krijgen we een systeem van twee vergelijkingen met twee onbekenden. Merk op dat de vrije termen (nummers 5 en 7) zich aan de linkerkant van de vergelijking bevinden. Over het algemeen maakt het niet uit waar ze zich bevinden, links of rechts, alleen zitten ze bij problemen in de hogere wiskunde vaak zo. En een dergelijke opname mag niet tot verwarring leiden; indien nodig kan het systeem altijd “zoals gebruikelijk” worden geschreven: . Vergeet niet dat wanneer u een term van deel naar deel verplaatst, het teken ervan moet veranderen.
Wat betekent het om een stelsel van lineaire vergelijkingen op te lossen? Het oplossen van een stelsel vergelijkingen betekent het vinden van veel van de oplossingen ervan. De oplossing van een systeem is een reeks waarden van alle variabelen die erin zijn opgenomen, waardoor ELKE vergelijking van het systeem in een echte gelijkheid verandert. Bovendien kan het systeem dat zijn niet-gezamenlijk (heb geen oplossingen) Wees niet verlegen, dit is een algemene definitie =) We zullen slechts één “x”-waarde en één “y”-waarde hebben, die aan elke c-we-vergelijking voldoen.
Er is een grafische methode om het systeem op te lossen, waarmee u in de klas vertrouwd kunt raken. De eenvoudigste problemen met een lijn. Daar heb ik het over gehad geometrische zin stelsels van twee lineaire vergelijkingen met twee onbekenden. Maar nu is dit het tijdperk van algebra, en getallen-getallen, acties-acties.
Laten we beslissen: uit de eerste vergelijking drukken we uit:
We vervangen de resulterende uitdrukking in de tweede vergelijking:
We openen de haakjes, voegen soortgelijke termen toe en vinden de waarde: 
Vervolgens herinneren we ons waarvoor we dansten:
We kennen de waarde al, het enige dat overblijft is het vinden van:
Antwoord:
Nadat ELK stelsel vergelijkingen op WELKE manier dan ook is opgelost, raad ik u ten zeerste aan dit te controleren (mondeling, op een concept of op een rekenmachine). Gelukkig gaat dit gemakkelijk en snel.
1) Vervang het gevonden antwoord in de eerste vergelijking:
– de juiste gelijkheid wordt verkregen.
2) Vervang het gevonden antwoord in de tweede vergelijking: ![]()
– de juiste gelijkheid wordt verkregen.
Of, eenvoudiger gezegd: “alles kwam samen”
De beschouwde oplossingsmethode is niet de enige; vanaf de eerste vergelijking was het mogelijk om uit te drukken, en niet.
Je kunt het tegenovergestelde doen: iets uit de tweede vergelijking uitdrukken en dit in de eerste vergelijking vervangen. Merk trouwens op dat de meest nadelige van de vier methoden is om uit te drukken op basis van de tweede vergelijking:
Het resultaat zijn breuken, maar waarom? Er is een meer rationele oplossing.
In sommige gevallen kun je echter nog steeds niet zonder breuken. In dit verband zou ik uw aandacht willen vestigen op HOE ik de uitdrukking heb opgeschreven. Niet zo: en in geen geval zo: ![]() .
.
Als je in de hogere wiskunde te maken hebt met breuken, probeer dan alle berekeningen uit te voeren in gewone onechte breuken.
Precies, en niet of!
Een komma kan slechts af en toe worden gebruikt, vooral als dit het definitieve antwoord is op een bepaald probleem en er geen verdere acties met dit getal hoeven te worden uitgevoerd.
Veel lezers dachten waarschijnlijk “waarom zo’n gedetailleerde uitleg als voor een correctieklasse, alles is duidelijk.” Niets van dat alles, het lijkt zo'n eenvoudig schoolvoorbeeld, maar er zijn zoveel ZEER belangrijke conclusies! Hier is er nog een:
Je moet ernaar streven elke taak op de meest rationele manier uit te voeren. Al was het maar omdat het tijd en zenuwen bespaart en bovendien de kans op fouten verkleint.
Als je bij een probleem in de hogere wiskunde een stelsel tegenkomt van twee lineaire vergelijkingen met twee onbekenden, dan kun je altijd de substitutiemethode gebruiken (tenzij aangegeven wordt dat het systeem op een andere manier opgelost moet worden). Geen enkele leraar zal dat doen. denk dat je een sukkel bent en dat je je cijfer verlaagt voor het gebruik van de “schoolmethode” "
Bovendien is het in sommige gevallen raadzaam om de substitutiemethode te gebruiken met een groter aantal variabelen.
Voorbeeld 2
Los een stelsel lineaire vergelijkingen op met drie onbekenden

Een soortgelijk systeem van vergelijkingen ontstaat vaak bij het gebruik van de zogenaamde methode van onbepaalde coëfficiënten, wanneer we de integraal van een fractionele rationale functie vinden. Het betreffende systeem is door mij daar vandaan gehaald.
Bij het vinden van de integraal is het doel: snel vind de waarden van de coëfficiënten, in plaats van de formules van Cramer, de inverse matrixmethode, enz. te gebruiken. Daarom is in dit geval de substitutiemethode geschikt.
Wanneer een systeem van vergelijkingen wordt gegeven, is het allereerst wenselijk om uit te zoeken of het mogelijk is om het ONMIDDELLIJK op de een of andere manier te vereenvoudigen? Als we de vergelijkingen van het systeem analyseren, merken we dat de tweede vergelijking van het systeem door 2 kan worden gedeeld, en dat is wat we doen:

Referentie: het wiskundige teken betekent “hieruit volgt dat” en wordt vaak gebruikt bij het oplossen van problemen.
Laten we nu de vergelijkingen analyseren; we moeten een variabele uitdrukken in termen van de andere. Welke vergelijking moet ik kiezen? Je raadde waarschijnlijk al dat de eenvoudigste manier om dit doel te bereiken is om de eerste vergelijking van het systeem te nemen:

Hier, ongeacht welke variabele je wilt uitdrukken, kun je net zo gemakkelijk of uitdrukken.
Vervolgens vervangen we de uitdrukking voor in de tweede en derde vergelijkingen van het systeem: 
We openen de haakjes en presenteren vergelijkbare termen: 
Deel de derde vergelijking door 2: 
Vanuit de tweede vergelijking drukken we uit en vervangen we deze in de derde vergelijking:

Bijna alles is klaar, uit de derde vergelijking vinden we:
Uit de tweede vergelijking: ![]()
Uit de eerste vergelijking:
Controle: vervang de gevonden waarden van de variabelen in de linkerkant van elke vergelijking van het systeem:
1)
2)
3)
De overeenkomstige rechterkanten van de vergelijkingen worden verkregen, waardoor de oplossing correct wordt gevonden.
Voorbeeld 3
Los een stelsel lineaire vergelijkingen op met 4 onbekenden

Dit is een voorbeeld dat u zelf kunt oplossen (antwoord aan het einde van de les).
Het systeem oplossen door term-voor-term optellen (aftrekken) van de systeemvergelijkingen
Bij het oplossen van systemen van lineaire vergelijkingen moet je proberen niet de "schoolmethode" te gebruiken, maar de methode van term voor term optellen (aftrekken) van de vergelijkingen van het systeem. Waarom? Dit bespaart tijd en vereenvoudigt de berekeningen, maar nu wordt alles duidelijker.
Voorbeeld 4
Los een stelsel lineaire vergelijkingen op: ![]()
Ik heb hetzelfde systeem genomen als in het eerste voorbeeld.
Als we het systeem van vergelijkingen analyseren, merken we dat de coëfficiënten van de variabele identiek zijn qua grootte en tegengesteld van teken (–1 en 1). In een dergelijke situatie kunnen de vergelijkingen term voor term worden toegevoegd: 
Acties die rood omcirkeld zijn, worden MENTAAL uitgevoerd.
Zoals u kunt zien, zijn we door het optellen van termen per term de variabele kwijtgeraakt. Dit is in feite wat de essentie van de methode is om van een van de variabelen af te komen.
§1. Systemen van lineaire vergelijkingen.
Systeem bekijken
een systeem genoemd M lineaire vergelijkingen met N onbekend.
Hier  - onbekend,
- onbekend,  - coëfficiënten voor onbekenden,
- coëfficiënten voor onbekenden,  - vrije termen van de vergelijkingen.
- vrije termen van de vergelijkingen.
Als alle vrije termen van de vergelijkingen gelijk zijn aan nul, wordt het systeem aangeroepen homogeen.Bij besluit systeem wordt een verzameling getallen genoemd  Wanneer we ze in het systeem vervangen in plaats van onbekenden, veranderen alle vergelijkingen in identiteiten. Het systeem wordt gebeld gewricht, als er minstens één oplossing is. Een compatibel systeem met een unieke oplossing wordt genoemd zeker. De twee systemen worden genoemd equivalent, als de sets van hun oplossingen samenvallen.
Wanneer we ze in het systeem vervangen in plaats van onbekenden, veranderen alle vergelijkingen in identiteiten. Het systeem wordt gebeld gewricht, als er minstens één oplossing is. Een compatibel systeem met een unieke oplossing wordt genoemd zeker. De twee systemen worden genoemd equivalent, als de sets van hun oplossingen samenvallen.
Systeem (1) kan in matrixvorm worden weergegeven met behulp van de vergelijking
 (2)
(2)
 .
.
§2. Compatibiliteit van systemen van lineaire vergelijkingen.
Laten we de uitgebreide matrix van systeem (1) de matrix noemen

Stelling van Kronecker-Capelli. Systeem (1) is consistent als en slechts als de rangorde van de systeemmatrix gelijk is aan de rangorde van de uitgebreide matrix:
 .
.
§3. SysteemoplossingN lineaire vergelijkingen metN onbekend.
Beschouw een inhomogeen systeem N lineaire vergelijkingen met N onbekend:
 (3)
(3)
De stelling van Cramer.Als de belangrijkste determinant van het systeem (3)  , dan heeft het systeem een unieke oplossing, bepaald door de formules:
, dan heeft het systeem een unieke oplossing, bepaald door de formules:

die.  ,
,
Waar  - determinant verkregen uit de determinant
- determinant verkregen uit de determinant  vervanging
vervanging  e kolom naar de kolom met vrije leden.
e kolom naar de kolom met vrije leden.
Als  , en tenminste één van
, en tenminste één van  ≠0, dan heeft het systeem geen oplossingen.
≠0, dan heeft het systeem geen oplossingen.
Als  , dan heeft het systeem oneindig veel oplossingen.
, dan heeft het systeem oneindig veel oplossingen.
Systeem (3) kan worden opgelost met behulp van zijn matrixvorm (2). Als de matrixrang A gelijk aan N, d.w.z.  en vervolgens de matrix A heeft een inverse
en vervolgens de matrix A heeft een inverse  . De matrixvergelijking vermenigvuldigen
. De matrixvergelijking vermenigvuldigen  naar de matrix
naar de matrix  aan de linkerkant krijgen we:
aan de linkerkant krijgen we:
 .
.
De laatste gelijkheid drukt de methode uit voor het oplossen van stelsels van lineaire vergelijkingen met behulp van een inverse matrix.
Voorbeeld. Los een stelsel vergelijkingen op met behulp van een inverse matrix.

Oplossing.
Matrix  niet-gedegenereerd, sindsdien
niet-gedegenereerd, sindsdien  , wat betekent dat er een inverse matrix is. Laten we de inverse matrix berekenen:
, wat betekent dat er een inverse matrix is. Laten we de inverse matrix berekenen:  .
.

 ,
,
Oefening. Los het systeem op met behulp van de methode van Cramer.
§4. Willekeurige stelsels van lineaire vergelijkingen oplossen.
Laten we een niet-homogeen systeem van lineaire vergelijkingen van de vorm (1) geven.
Laten we aannemen dat het systeem consistent is, d.w.z. aan de voorwaarde van de stelling van Kronecker-Capelli is voldaan:  . Als de matrixrang
. Als de matrixrang  (aantal onbekenden), dan heeft het systeem een unieke oplossing. Als
(aantal onbekenden), dan heeft het systeem een unieke oplossing. Als  , dan heeft het systeem oneindig veel oplossingen. Laat het me uitleggen.
, dan heeft het systeem oneindig veel oplossingen. Laat het me uitleggen.
Laten we de rangorde van de matrix bepalen R(A)=
R<
N. Omdat de  , dan is er een minder belangrijke orde dan nul R. Laten we het de basisminor noemen. De onbekenden waarvan de coëfficiënten een basisminor vormen, worden basisvariabelen genoemd. De resterende onbekenden noemen we vrije variabelen. Laten we de vergelijkingen herschikken en de variabelen opnieuw nummeren, zodat deze minor zich in de linkerbovenhoek van de systeemmatrix bevindt:
, dan is er een minder belangrijke orde dan nul R. Laten we het de basisminor noemen. De onbekenden waarvan de coëfficiënten een basisminor vormen, worden basisvariabelen genoemd. De resterende onbekenden noemen we vrije variabelen. Laten we de vergelijkingen herschikken en de variabelen opnieuw nummeren, zodat deze minor zich in de linkerbovenhoek van de systeemmatrix bevindt:
 .
.
Eerst R lijnen zijn lineair onafhankelijk, de rest wordt daardoor uitgedrukt. Daarom kunnen deze lijnen (vergelijkingen) worden weggegooid. We krijgen:

Laten we de vrije variabelen willekeurige numerieke waarden geven: . Laten we alleen de basisvariabelen aan de linkerkant laten staan en de vrije variabelen naar de rechterkant verplaatsen.

Ik heb het systeem R lineaire vergelijkingen met R onbekend, waarvan de determinant anders is dan 0. Het heeft een unieke oplossing.

Dit systeem wordt de algemene oplossing van het stelsel lineaire vergelijkingen (1) genoemd. Anders: de uitdrukking van basisvariabelen door middel van vrije variabelen wordt genoemd algemeen besluit systemen. Hieruit kun je een oneindig aantal halen particuliere oplossingen, waardoor vrije variabelen willekeurige waarden krijgen. Een specifieke oplossing verkregen uit een algemene oplossing voor nulwaarden van vrije variabelen wordt genoemd basisoplossing. Het aantal verschillende basisoplossingen is niet groter dan  . Een basisoplossing met niet-negatieve componenten wordt genoemd ondersteunen systeem oplossing.
. Een basisoplossing met niet-negatieve componenten wordt genoemd ondersteunen systeem oplossing.
Voorbeeld.
 ,R=2.
,R=2.
Variabelen  - basis,
- basis,  - vrij.
- vrij.
Laten we de vergelijkingen bij elkaar optellen; laten we uitdrukken  door
door  :
:
 - gemeenschappelijk besluit.
- gemeenschappelijk besluit.
 - particuliere oplossing voor
- particuliere oplossing voor  .
.
 - basisoplossing, referentie.
- basisoplossing, referentie.
§5. Gauss-methode.
De Gauss-methode is een universele methode voor het bestuderen en oplossen van willekeurige systemen van lineaire vergelijkingen. Het bestaat uit het reduceren van het systeem tot een diagonale (of driehoekige) vorm door opeenvolgend onbekenden te elimineren met behulp van elementaire transformaties die de gelijkwaardigheid van systemen niet schenden. Een variabele wordt als uitgesloten beschouwd als deze slechts in één vergelijking van het systeem met een coëfficiënt van 1 voorkomt.
Elementaire transformaties systemen zijn:
Een vergelijking vermenigvuldigen met een ander getal dan nul;
Een vergelijking optellen vermenigvuldigd met een willekeurig getal met een andere vergelijking;
Vergelijkingen herschikken;
Het verwerpen van de vergelijking 0 = 0.
Elementaire transformaties kunnen niet worden uitgevoerd op vergelijkingen, maar op uitgebreide matrices van de resulterende equivalente systemen.
Voorbeeld.

Oplossing. Laten we de uitgebreide matrix van het systeem opschrijven:
 .
.
Door elementaire transformaties uit te voeren, zullen we de linkerkant van de matrix terugbrengen tot eenheidsvorm: we zullen enen creëren op de hoofddiagonaal en nullen daarbuiten.











Opmerking. Als bij het uitvoeren van elementaire transformaties een vergelijking van de vorm 0 wordt verkregen = k(Waar Naar 0),
dan is het systeem inconsistent.
0),
dan is het systeem inconsistent.
De oplossing van systemen van lineaire vergelijkingen door de methode van opeenvolgende eliminatie van onbekenden kan in de vorm worden geschreven tafels.
De linkerkolom van de tabel bevat informatie over uitgesloten (basis)variabelen. De overige kolommen bevatten de coëfficiënten van de onbekenden en de vrije termen van de vergelijkingen.
De uitgebreide matrix van het systeem wordt vastgelegd in de brontabel. Vervolgens beginnen we Jordan-transformaties uit te voeren:
1. Selecteer een variabele  , wat de basis zal worden. De bijbehorende kolom wordt de sleutelkolom genoemd. Kies een vergelijking waarin deze variabele blijft bestaan, omdat hij wordt uitgesloten van andere vergelijkingen. De bijbehorende tabelrij wordt een sleutelrij genoemd. Coëfficiënt
, wat de basis zal worden. De bijbehorende kolom wordt de sleutelkolom genoemd. Kies een vergelijking waarin deze variabele blijft bestaan, omdat hij wordt uitgesloten van andere vergelijkingen. De bijbehorende tabelrij wordt een sleutelrij genoemd. Coëfficiënt  , die op het kruispunt van een sleutelrij en een sleutelkolom staat, wordt een sleutel genoemd.
, die op het kruispunt van een sleutelrij en een sleutelkolom staat, wordt een sleutel genoemd.
2. De sleutelreekselementen zijn onderverdeeld in het sleutelelement.
3. De sleutelkolom is gevuld met nullen.
4. De overige elementen worden berekend met behulp van de rechthoekregel. Maak een rechthoek, op de tegenoverliggende hoekpunten bevindt zich een sleutelelement en een herberekend element; van het product van de elementen op de diagonaal van de rechthoek met het sleutelelement, wordt het product van de elementen van de andere diagonaal afgetrokken en het resulterende verschil gedeeld door het sleutelelement.
Voorbeeld. Vind de algemene oplossing en de basisoplossing van het stelsel vergelijkingen:

Oplossing.
|
|
|
|
|
|
|
|
|
| ||||||
|
| ||||||
|
|
Algemene oplossing van het systeem:

Basisoplossing:  .
.
Met een enkele substitutietransformatie kunt u van de ene basis van het systeem naar de andere gaan: in plaats van een van de hoofdvariabelen wordt een van de vrije variabelen in de basis geïntroduceerd. Om dit te doen, selecteert u een sleutelelement in de vrije variabelekolom en voert u transformaties uit volgens het bovenstaande algoritme.
§6. Het vinden van ondersteunende oplossingen
De referentieoplossing van een stelsel lineaire vergelijkingen is een basisoplossing die geen negatieve componenten bevat.
De referentieoplossingen van het systeem worden gevonden met de Gaussische methode wanneer aan de volgende voorwaarden wordt voldaan.
1. In het oorspronkelijke systeem moeten alle vrije termen niet-negatief zijn:  .
.
2. Het sleutelelement wordt geselecteerd uit de positieve coëfficiënten.
3. Als een in de basis geïntroduceerde variabele meerdere positieve coëfficiënten heeft, dan is de hoofdlijn degene waarin de verhouding tussen de vrije term en de positieve coëfficiënt het kleinst is.
Notitie 1. Als er tijdens het elimineren van onbekenden een vergelijking verschijnt waarin alle coëfficiënten niet-positief zijn en de vrije term zijn  , dan heeft het systeem geen niet-negatieve oplossingen.
, dan heeft het systeem geen niet-negatieve oplossingen.
Opmerking 2. Als er geen enkel positief element in de kolommen met coëfficiënten voor vrije variabelen staat, is de overgang naar een andere referentieoplossing onmogelijk.
Voorbeeld.

|
|
|














