Den maksimale egenverdien til en matrise. Matrise karakteristisk ligning

Diagonal-type matriser er enklest ordnet. Spørsmålet oppstår om det er mulig å finne et grunnlag der matrisen til en lineær operator ville ha en diagonal form. Et slikt grunnlag finnes.
La et lineært rom R n og en lineær operator A som virker i det gis; i dette tilfellet tar operatøren A R n inn i seg selv, det vil si A:R n → R n .

Definisjon. En vektor som ikke er null kalles en egenvektor til operatoren A hvis operatoren A oversettes til en vektor som er kolineær til den, det vil si . Tallet λ kalles egenverdien eller egenverdien til operatoren A som tilsvarer egenvektoren.
Vi legger merke til noen egenskaper til egenverdier og egenvektorer.
1. Enhver lineær kombinasjon av egenvektorer av operatoren A som svarer til samme egenverdi λ er en egenvektor med samme egenverdi.
2. Egenvektorer operator A med parvis distinkte egenverdier λ 1 , λ 2 , …, λ m er lineært uavhengige.
3. Hvis egenverdiene λ 1 =λ 2 = λ m = λ, så tilsvarer egenverdien λ ikke mer enn m lineært uavhengige egenvektorer.

Så hvis det er n lineært uavhengige egenvektorer svarende til forskjellige egenverdier λ 1 , λ 2 , …, λ n , så er de lineært uavhengige, derfor kan de tas som grunnlag for rommet R n . La oss finne formen til matrisen til den lineære operatøren A på grunnlag av dens egenvektorer, for hvilke vi handler med operatøren A på basisvektorene: deretter .
Dermed har matrisen til den lineære operatoren A på grunnlag av egenvektorene en diagonal form, og egenverdiene til operatoren A er på diagonalen.
Er det et annet grunnlag der matrisen har en diagonal form? Svaret på dette spørsmålet er gitt av følgende teorem.

Teorem. Matrisen til en lineær operator A i basisen (i = 1..n) har en diagonal form hvis og bare hvis alle vektorene til basisen er egenvektorer til operatoren A.

Regel for å finne egenverdier og egenvektorer

. (*)

(1)
hvor er matrisen til den lineære operatoren.

System (1) har en løsning som ikke er null hvis determinanten D er lik null

Eksempel 12. Den lineære operatoren A virker i R 3 i henhold til loven , hvor x 1 , x 2 , .., x n er koordinatene til vektoren i basisen , , . Finn egenverdiene og egenvektorene til denne operatoren.
Løsning. Vi bygger matrisen til denne operatøren:
.
Vi komponerer et system for å bestemme koordinatene til egenvektorer:

Vi komponerer den karakteristiske ligningen og løser den:

.
λ 1,2 = -1, λ 3 = 3.
Ved å erstatte λ = -1 i systemet, har vi:
eller
Fordi , så er det to avhengige variabler og en fri variabel.
La x 1 være en ledig ukjent, da Vi løser dette systemet på hvilken som helst måte og finner den generelle løsningen til dette systemet: Det grunnleggende løsningssystemet består av én løsning, siden n - r = 3 - 2 = 1.
Settet med egenvektorer som tilsvarer egenverdien λ = -1 har formen: , hvor x 1 er et hvilket som helst annet tall enn null. La oss velge en vektor fra dette settet, for eksempel ved å sette x 1 = 1: .
Ved å argumentere på samme måte finner vi egenvektoren som tilsvarer egenverdien λ = 3: .
I rommet R 3 består basisen av tre lineært uavhengige vektorer, men vi har kun fått to lineært uavhengige egenvektorer, som basisen i R 3 ikke kan dannes fra. Følgelig kan ikke matrisen A til en lineær operator reduseres til en diagonal form.

Eksempel 13 Gitt en matrise .
1. Bevis at vektoren er en egenvektor til matrisen A. Finn egenverdien som tilsvarer denne egenvektoren.
2. Finn et grunnlag der matrisen A har diagonal form.
Løsning.
1. Hvis , så er en egenvektor

.
Vektor (1, 8, -1) er en egenvektor. Egenverdi λ = -1.
Matrisen har en diagonal form i grunnlaget bestående av egenvektorer. En av dem er kjent. La oss finne resten.
Vi ser etter egenvektorer fra systemet:

Karakteristisk ligning: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Finn egenvektoren som tilsvarer egenverdien λ = -3:

Rangeringen av matrisen til dette systemet er lik to og er lik antall ukjente, derfor har dette systemet bare en nullløsning x 1 = x 3 = 0. x 2 her kan være alt annet enn null, for eksempel, x 2 = 1. Dermed er vektoren (0 ,1,0) en egenvektor som tilsvarer λ = -3. La oss sjekke:
.
Hvis λ = 1, får vi systemet
Rangeringen av matrisen er to. Kryss ut den siste ligningen.
La x 3 være den frie ukjente. Deretter x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Forutsatt at x 3 = 1, har vi (-3,-9,1) - en egenvektor som tilsvarer egenverdien λ = 1. Sjekk:

.
Siden egenverdiene er reelle og forskjellige, er vektorene som tilsvarer dem lineært uavhengige, så de kan tas som grunnlag i R 3 . Altså i grunnlaget , , matrise A har formen:
.
Ikke hver matrise av en lineær operator A:R n → R n kan reduseres til en diagonal form, siden det for noen lineære operatorer kan være mindre enn n lineært uavhengige egenvektorer. Imidlertid, hvis matrisen er symmetrisk, tilsvarer nøyaktig m lineært uavhengige vektorer roten til den karakteristiske ligningen av multiplisitet m.

Definisjon. En symmetrisk matrise er en kvadratisk matrise der elementene som er symmetriske i forhold til hoveddiagonalen er like, det vil si hvor .
Merknader. 1. Alle egenverdier til en symmetrisk matrise er reelle.
2. Egenvektorer til en symmetrisk matrise som tilsvarer parvis forskjellige egenverdier er ortogonale.
Som en av de mange anvendelsene av det studerte apparatet, vurderer vi problemet med å bestemme formen til en andreordenskurve.

Definisjon 9.3. Vektor X kalt egen vektor matriser EN hvis det er et slikt tall λ, at likestillingen gjelder: EN X= λ X, det vil si resultatet av å søke på X lineær transformasjon gitt av matrisen EN, er multiplikasjonen av denne vektoren med tallet λ . Selve nummeret λ kalt eget nummer matriser EN.

Bytte inn i formler (9.3) x` j = λx j , vi får et likningssystem for å bestemme koordinatene til egenvektoren:

. (9.5)

Dette lineære homogene systemet vil bare ha en ikke-triviell løsning hvis hoveddeterminanten er 0 (Cramers regel). Ved å skrive denne betingelsen i skjemaet:

får vi en ligning for å bestemme egenverdiene λ kalt karakteristisk ligning. Kort fortalt kan det representeres som følger:

| A-λE | = 0, (9.6)

siden dens venstre side er determinanten for matrisen A-λE. Polynom med hensyn til λ | A-λE| kalt karakteristisk polynom matriser a.

Egenskaper til det karakteristiske polynomet:

1) Det karakteristiske polynomet til en lineær transformasjon er ikke avhengig av valget av grunnlaget. Bevis. (se (9.4)), men derfor,. Avhenger dermed ikke av valg av grunnlag. Derfor, og | A-λE| endres ikke ved overgang til nytt grunnlag.

2) Hvis matrisen EN lineær transformasjon er symmetrisk(de. a ij = en ji), så er alle røttene til den karakteristiske ligningen (9.6) reelle tall.

Egenskaper til egenverdier og egenvektorer:

1) Hvis vi velger et grunnlag fra egenvektorer x 1, x 2, x 3 tilsvarende egenverdiene λ 1 , λ 2 , λ 3 matriser EN, så har den lineære transformasjonen A på dette grunnlaget en diagonal matrise:

(9.7) Beviset for denne egenskapen følger av definisjonen av egenvektorer.

2) Hvis transformasjonens egenverdier EN er forskjellige, så er egenvektorene som tilsvarer dem lineært uavhengige.

3) Hvis det karakteristiske polynomet til matrisen EN har tre forskjellige røtter, deretter på et eller annet grunnlag matrisen EN har en diagonal form.

La oss finne egenverdiene og egenvektorene til matrisen La oss lage den karakteristiske ligningen: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Finn koordinatene til egenvektorene som tilsvarer hver funnet verdi λ. Av (9.5) følger det at if X (1) ={x 1, x 2, x 3) er egenvektoren som tilsvarer λ 1 = -2, da

er et samarbeidende, men ubestemt system. Løsningen kan skrives som X (1) ={en,0,-en), der a er et hvilket som helst tall. Spesielt hvis du krever at | x (1) |=1, X (1) =

Bytter inn i systemet (9.5) λ 2 =3, får vi et system for å bestemme koordinatene til den andre egenvektoren - x (2) ={y1,y2,y3}:

, hvor X (2) ={b,-b,b) eller, forutsatt | x (2) |=1, x (2) =

Til λ 3 = 6 finn egenvektoren x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) eller i normalisert versjon

x (3) = Det kan man se X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = f.Kr- 2bc + bc= 0. Dermed er egenvektorene til denne matrisen parvis ortogonale.

Forelesning 10

Kvadratiske former og deres sammenheng med symmetriske matriser. Egenskaper til egenvektorer og egenverdier til en symmetrisk matrise. Reduksjon av en kvadratisk form til en kanonisk form.

Definisjon 10.1.kvadratisk form reelle variabler x 1, x 2,..., x n er et polynom av andre grad med hensyn til disse variablene som ikke inneholder et fritt ledd og termer av første grad.

Eksempler på kvadratiske former:

(n = 2),

(n = 3). (10.1)

Husk definisjonen av en symmetrisk matrise gitt i siste forelesning:

Definisjon 10.2. Den kvadratiske matrisen kalles symmetrisk, hvis , det vil si hvis matriseelementene symmetriske med hensyn til hoveddiagonalen er like.

Egenskaper til egenverdier og egenvektorer til en symmetrisk matrise:

1) Alle egenverdier til en symmetrisk matrise er reelle.

Bevis (for n = 2).

La matrisen EN ser ut som: . La oss lage den karakteristiske ligningen:

(10.2) Finn diskriminanten:

Derfor har ligningen bare reelle røtter.

2) Egenvektorene til en symmetrisk matrise er ortogonale.

Bevis (for n= 2).

Koordinatene til egenvektorene og må tilfredsstille ligningene.

SYSTEM AV HOMOGENE LINEÆRE LIGNINGER

Et system med homogene lineære ligninger er et formsystem

Det er klart at i dette tilfellet , fordi alle elementene i en av kolonnene i disse determinantene er lik null.

Siden de ukjente finnes av formlene , så i tilfellet når Δ ≠ 0, har systemet en unik nullløsning x = y = z= 0. Men i mange problemer er spørsmålet om et homogent system har andre løsninger enn null av interesse.

Teorem. For at et system med lineære homogene ligninger skal ha en løsning som ikke er null, er det nødvendig og tilstrekkelig at Δ ≠ 0.

Så hvis determinanten er Δ ≠ 0, så har systemet en unik løsning. Hvis Δ ≠ 0, så har systemet med lineære homogene ligninger et uendelig antall løsninger.

Eksempler.

Egenvektorer og matriseegenverdier

La en kvadratisk matrise gis , X er en matrise-kolonne hvis høyde sammenfaller med rekkefølgen til matrisen EN. .

I mange problemer må man vurdere ligningen for X

hvor λ er et tall. Det er klart at for enhver λ har denne ligningen en nullløsning.

Tallet λ som denne ligningen har løsninger som ikke er null kalles egenverdi matriser EN, a X for slikt kalles λ egen vektor matriser EN.

La oss finne egenvektoren til matrisen EN. For så vidt E∙X=X, så kan matriseligningen skrives om som eller . I utvidet form kan denne ligningen skrives om som et system av lineære ligninger. Egentlig .

Og derfor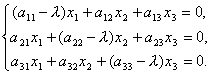

Så vi har et system med homogene lineære ligninger for å bestemme koordinatene x 1, x2, x 3 vektor X. For at systemet skal ha løsninger som ikke er null, er det nødvendig og tilstrekkelig at determinanten til systemet er lik null, dvs.

Dette er en 3. grads ligning med hensyn til λ. Det heter karakteristisk ligning matriser EN og tjener til å bestemme egenverdiene λ.

Hver egenverdi λ tilsvarer en egenvektor X, hvis koordinater bestemmes fra systemet ved den tilsvarende verdien av λ.

Eksempler.

VEKTORALGEBRA. VEKTOR KONSEPT

Når du studerer ulike grener av fysikk, er det mengder som er fullstendig bestemt ved å sette deres numeriske verdier, for eksempel lengde, areal, masse, temperatur, etc. Slike verdier kalles skalar. Men i tillegg til dem er det også mengder, for bestemmelsen av hvilke, i tillegg til den numeriske verdien, det også er nødvendig å vite retningen deres i rommet, for eksempel kraften som virker på kroppen, hastigheten og akselerasjonen. av kroppen når den beveger seg i rommet, magnetfeltstyrken på et gitt punkt i rommet og etc. Slike mengder kalles vektormengder.

La oss introdusere en streng definisjon.

Retningsbestemt segment La oss kalle et segment, i forhold til endene som det er kjent hvilken av dem som er den første og hvilken som er den andre.

Vektor et rettet segment kalles, som har en viss lengde, dvs. Dette er et segment av en viss lengde, der ett av punktene som begrenser det tas som begynnelsen, og det andre - som slutten. Hvis EN er begynnelsen av vektoren, B er slutten, så er vektoren betegnet med symbolet, i tillegg er vektoren ofte betegnet med en enkelt bokstav . På figuren er vektoren indikert med et segment, og retningen med en pil.

modul eller lengde vektor kalles lengden på det rettede segmentet som definerer det. Angitt med || eller ||.

Den såkalte nullvektoren, hvis begynnelse og slutt faller sammen, vil også bli referert til som vektorer. Det er merket. Nullvektoren har ingen bestemt retning og dens modul er lik null ||=0.

Vektorer og kalles kollineær hvis de er plassert på samme linje eller på parallelle linjer. I dette tilfellet, hvis vektorene og er likt rettet, vil vi skrive , motsatt.

Vektorer plassert på rette linjer parallelt med samme plan kalles koplanar.

To vektorer og kalles lik hvis de er kollineære, har samme retning og er like lange. Skriv i dette tilfellet.

Det følger av definisjonen av vektorlikhet at en vektor kan flyttes parallelt med seg selv ved å plassere sin opprinnelse på et hvilket som helst punkt i rommet.

for eksempel.

LINEÆRE OPERASJONER PÅ VEKTORER

1. Multiplisere en vektor med et tall.

   Produktet av en vektor med et tall λ er en ny vektor slik at:

   Produktet av en vektor og et tall λ er merket med .

   

   For eksempel, er en vektor som peker i samme retning som vektoren og har en lengde som er halvparten av vektoren.

   Den angitte operasjonen har følgende egenskaper:

2. Addisjon av vektorer.

   La og være to vilkårlige vektorer. Ta et vilkårlig poeng O og konstruer en vektor. Etter det, fra poenget EN sett til side vektoren. Vektoren som forbinder begynnelsen av den første vektoren med slutten av den andre kalles sum av disse vektorene og er betegnet .

   

   Den formulerte definisjonen av vektoraddisjon kalles parallellogramregel, siden samme sum av vektorer kan oppnås som følger. Sett til side fra poenget O vektorer og . Konstruer et parallellogram på disse vektorene OABC. Siden vektorene, så vektoren, som er diagonalen til parallellogrammet trukket fra toppunktet O, vil åpenbart være summen av vektorer.

   

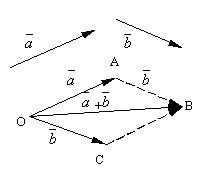
   Det er enkelt å sjekke følgende vektoraddisjonsegenskaper.

3. Forskjell mellom vektorer.

   En vektor kollineær til en gitt vektor, lik lengde og motsatt rettet, kalles motsatte vektor for en vektor og er betegnet med . Den motsatte vektoren kan betraktes som resultatet av vektormultiplikasjon med tallet λ = –1: .

En egenvektor til en kvadratisk matrise er en som, multiplisert med en gitt matrise, resulterer i en kollineær vektor. Med enkle ord, når en matrise multipliseres med en egenvektor, forblir sistnevnte den samme, men multiplisert med et eller annet tall.

Definisjon

En egenvektor er en ikke-null vektor V, som, når multiplisert med en kvadratisk matrise M, blir seg selv, økt med et eller annet tall λ. I algebraisk notasjon ser dette slik ut:

M × V = λ × V,

hvor λ er en egenverdi til matrisen M.

La oss vurdere et numerisk eksempel. For å gjøre det enklere å skrive, vil tallene i matrisen være atskilt med et semikolon. La oss si at vi har en matrise:

• M = 0; 4;
• 6; 10.

La oss multiplisere det med en kolonnevektor:

• V = -2;

Når vi multipliserer en matrise med en kolonnevektor, får vi også en kolonnevektor. I strengt matematisk språk vil formelen for å multiplisere en 2 × 2 matrise med en kolonnevektor se slik ut:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 betyr elementet i matrisen M, som står i den første raden og den første kolonnen, og M22 er elementet i den andre raden og den andre kolonnen. For matrisen vår er disse elementene M11 = 0, M12 = 4, M21 = 6, M22 10. For en kolonnevektor er disse verdiene V11 = –2, V21 = 1. I følge denne formelen får vi følgende resultat av produktet av en kvadratisk matrise med en vektor:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

For enkelhets skyld skriver vi kolonnevektoren i en rad. Så vi har multiplisert kvadratmatrisen med vektoren (-2; 1), noe som resulterer i vektoren (4; -2). Det er klart at dette er den samme vektoren multiplisert med λ = -2. Lambda i dette tilfellet angir en egenverdi til matrisen.

En egenvektor til en matrise er en kollineær vektor, det vil si et objekt som ikke endrer sin posisjon i rommet når det multipliseres med en matrise. Konseptet med kollinearitet i vektoralgebra ligner på begrepet parallellisme i geometri. I geometrisk tolkning er kollineære vektorer parallellrettede segmenter av forskjellig lengde. Siden Euklids tid vet vi at en enkelt linje har et uendelig antall linjer parallelle med seg, så det er logisk å anta at hver matrise har et uendelig antall egenvektorer.

Fra forrige eksempel kan man se at både (-8; 4), og (16; -8), og (32, -16) kan være egenvektorer. Alle disse er kollineære vektorer som tilsvarer egenverdien λ = -2. Når vi multipliserer den opprinnelige matrisen med disse vektorene, vil vi fortsatt få en vektor som et resultat, som avviker fra originalen med 2 ganger. Det er derfor, når du løser problemer for å finne en egenvektor, er det nødvendig å finne bare lineært uavhengige vektorobjekter. Oftest, for en n × n matrise, er det n-te antall egenvektorer. Kalkulatoren vår er designet for analyse av andreordens kvadratmatriser, så nesten alltid to egenvektorer vil bli funnet som et resultat, bortsett fra når de faller sammen.

I eksemplet ovenfor kjente vi på forhånd egenvektoren til den opprinnelige matrisen og bestemte lambdatallet visuelt. Men i praksis skjer alt omvendt: i begynnelsen er det egenverdier og først da egenvektorer.

Løsningsalgoritme

La oss se på den opprinnelige matrisen M igjen og prøve å finne begge dens egenvektorer. Så matrisen ser slik ut:

• M = 0; 4;
• 6; 10.

Til å begynne med må vi bestemme egenverdien λ, som vi må beregne determinanten for følgende matrise for:

• (0 - λ); 4;
• 6; (10 − λ).

Denne matrisen oppnås ved å trekke den ukjente λ fra elementene på hoveddiagonalen. Determinanten bestemmes av standardformelen:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Siden vektoren vår ikke må være null, tar vi den resulterende ligningen som lineært avhengig og likestiller vår determinant detA til null.

(0 − λ) × (10 − λ) − 24 = 0

La oss åpne parentesene og få den karakteristiske ligningen til matrisen:

λ 2 − 10λ − 24 = 0

Dette er en standard andregradsligning som må løses i form av diskriminanten.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Roten til diskriminanten er sqrt(D) = 14, så λ1 = -2, λ2 = 12. Nå for hver lambda-verdi må vi finne en egenvektor. La oss uttrykke koeffisientene til systemet for λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

I denne formelen er E identitetsmatrisen. Basert på den oppnådde matrisen, komponerer vi et system med lineære ligninger:

2x + 4y = 6x + 12y

hvor x og y er elementer i egenvektoren.

La oss samle alle X-ene til venstre og alle Y-ene til høyre. Tydeligvis - 4x = 8y. Del uttrykket med - 4 og få x = -2y. Nå kan vi bestemme den første egenvektoren til matrisen ved å ta alle verdier av de ukjente (husk om uendeligheten til lineært avhengige egenvektorer). La oss ta y = 1, så x = -2. Derfor ser den første egenvektoren ut som V1 = (–2; 1). Gå tilbake til begynnelsen av artikkelen. Det var dette vektorobjektet vi multipliserte matrisen med for å demonstrere konseptet med en egenvektor.

La oss nå finne egenvektoren for λ = 12.

• M - X × E = -12; 4
• 6; -2.

La oss komponere det samme systemet med lineære ligninger;

• -12x + 4y = 6x - 2y
• -18x = -6y
• 3x=y.

La oss nå ta x = 1, derav y = 3. Dermed ser den andre egenvektoren ut som V2 = (1; 3). Når du multipliserer den opprinnelige matrisen med denne vektoren, vil resultatet alltid være den samme vektoren multiplisert med 12. Dette fullfører løsningsalgoritmen. Nå vet du hvordan du manuelt definerer en egenvektor til en matrise.

• avgjørende faktor;
• spor, det vil si summen av elementene på hoveddiagonalen;
• rangering, dvs. maksimalt antall lineært uavhengige rader/kolonner.

Programmet fungerer i henhold til algoritmen ovenfor, og minimerer løsningsprosessen. Det er viktig å påpeke at i programmet er lambdaen merket med bokstaven "c". La oss se på et numerisk eksempel.

Programeksempel

La oss prøve å definere egenvektorer for følgende matrise:

• M=5; tretten;
• 4; 14.

La oss legge inn disse verdiene i cellene til kalkulatoren og få svaret i følgende skjema:

• Matriserangering: 2;
• Matrisedeterminant: 18;
• Matrisespor: 19;
• Egenvektorberegning: c 2 − 19,00c + 18,00 (karakteristisk ligning);
• Egenvektorberegning: 18 (første lambdaverdi);
• Egenvektorberegning: 1 (andre lambdaverdi);
• Ligningssystem av vektor 1: -13x1 + 13y1 = 4x1 − 4y1;
• Vektor 2 ligningssystem: 4x1 + 13y1 = 4x1 + 13y1;
• Egenvektor 1: (1; 1);
• Egenvektor 2: (-3,25; 1).

Dermed har vi fått to lineært uavhengige egenvektorer.

Konklusjon

Lineær algebra og analytisk geometri er standardfag for enhver nybegynner i ingeniørfag. Et stort antall vektorer og matriser er skremmende, og det er lett å gjøre feil i slike tungvinte beregninger. Programmet vårt lar studentene sjekke beregningene sine eller automatisk løse problemet med å finne en egenvektor. Det er andre lineære algebrakalkulatorer i vår katalog, bruk dem i studiet eller arbeidet ditt.

www.nettsted lar deg finne. Nettstedet gjør beregningen. I løpet av noen få sekunder vil serveren gi den riktige løsningen. Den karakteristiske ligningen for matrisen vil være et algebraisk uttrykk funnet av regelen for beregning av determinanten matriser matriser, mens på hoveddiagonalen vil det være forskjeller i verdiene til diagonalelementene og variabelen. Ved beregning karakteristisk ligning for matrise online, hvert element matriser vil bli multiplisert med de tilsvarende andre elementene matriser. Finn i modus på nett bare mulig for firkantet matriser. Finn operasjon karakteristisk ligning for matrise online reduserer til å beregne den algebraiske summen av produktet av elementer matriser som et resultat av å finne determinanten matriser, bare med det formål å bestemme karakteristisk ligning for matrise online. Denne operasjonen inntar en spesiell plass i teorien matriser, lar deg finne egenverdier og vektorer ved å bruke røtter . Finner oppgave karakteristisk ligning for matrise online er å multiplisere elementer matriser med påfølgende summering av disse produktene i henhold til en viss regel. www.nettsted finner karakteristisk ligning for matrise gitt dimensjon i modusen på nett. beregning karakteristisk ligning for matrise online for en gitt dimensjon er dette å finne et polynom med numeriske eller symbolske koeffisienter funnet av regelen for å beregne determinanten matriser- som summen av produktene til de tilsvarende elementene matriser, bare med det formål å bestemme karakteristisk ligning for matrise online. Finne et polynom med hensyn til en variabel for en kvadrat matriser, som definisjon karakteristisk ligning for matrisen, vanlig i teorien matriser. Verdien av røttene til polynomet karakteristisk ligning for matrise online brukes til å definere egenvektorer og egenverdier for matriser. Imidlertid, hvis determinanten matriser vil da være null matrisekarakteristisk ligning vil fortsatt eksistere, i motsetning til det motsatte matriser. For å beregne karakteristisk ligning for matrise eller søk etter flere samtidig matriser karakteristiske ligninger, må du bruke mye tid og krefter, mens serveren vår vil finne karakteristisk ligning for nettmatrise. I dette tilfellet, svaret ved å finne karakteristisk ligning for matrise online vil være korrekt og med tilstrekkelig nøyaktighet, selv om tallene ved funn karakteristisk ligning for matrise online vil være irrasjonelt. På siden www.nettsted tegnoppføringer er tillatt i elementer matriser, det er karakteristisk ligning for nettmatrise kan representeres i en generell symbolsk form ved beregning karakteristisk ligningsmatrise online. Det er nyttig å sjekke svaret som er oppnådd når du løser problemet med å finne karakteristisk ligning for matrise online bruker nettstedet www.nettsted. Når du utfører operasjonen med å beregne et polynom - karakteristisk ligning for matrisen, er det nødvendig å være oppmerksom og ekstremt konsentrert for å løse dette problemet. På sin side vil nettstedet vårt hjelpe deg med å sjekke avgjørelsen din om emnet karakteristisk ligningsmatrise online. Hvis du ikke har tid til lange kontroller av løste problemer, da www.nettsted vil helt sikkert være et praktisk verktøy for å sjekke når du skal finne og regne karakteristisk ligning for matrise online.