أقصى قيمة ذاتية لمصفوفة. معادلة خصائص المصفوفة

يتم ترتيب المصفوفات من النوع القطري ببساطة. السؤال الذي يطرح نفسه هو ما إذا كان من الممكن إيجاد أساس يكون لمصفوفة عامل خطي شكل قطري. مثل هذا الأساس موجود.
دع مساحة خطية R n والمشغل الخطي A يعمل فيه ؛ في هذه الحالة ، يأخذ المشغل A R n في نفسه ، أي A: R n → R n.

تعريف. يُطلق على المتجه غير الصفري اسم المتجه الذاتي للمشغل A إذا تمت ترجمة المشغل A إلى متجه خطي متواصل ، أي. الرقم λ يسمى eigenvalue أو eigenvalue للمشغل A المقابل لـ eigenvector.
نلاحظ بعض خصائص القيم الذاتية والمتجهات الذاتية.
1. أي مجموعة خطية من المتجهات الذاتية من المشغل A المقابلة لنفس القيمة الذاتية هي متجه ذاتي مع نفس القيمة الذاتية.
2. المتجهات الذاتية عامل التشغيل A بقيم ذاتية مميزة زوجية λ 1 ، λ 2 ، ... ، λ m مستقلة خطيًا.
3. إذا كانت قيم eigenvalue λ 1 = 2 = λ m = ، فإن القيمة الذاتية لا تتوافق مع أكثر من m متجهات ذاتية مستقلة خطيًا.

لذلك ، إذا كان هناك n متجهات ذاتية مستقلة خطيًا المقابلة لقيم ذاتية مختلفة λ 1 ، λ 2 ، ... ، n ، ثم تكون مستقلة خطيًا ، وبالتالي ، يمكن اعتبارها أساس الفضاء R n. دعونا نجد شكل مصفوفة العامل الخطي A في أساس متجهاتها الذاتية ، والتي من أجلها نتعامل مع المشغل A على أساس المتجهات: من ثم .
وبالتالي ، فإن مصفوفة العامل الخطي A في أساس متجهاتها الذاتية لها شكل قطري ، والقيم الذاتية للمشغل A على القطر.
هل هناك أساس آخر تكون فيه المصفوفة قطرية؟ يتم إعطاء إجابة هذا السؤال من خلال النظرية التالية.

نظرية. مصفوفة العامل الخطي A في الأساس (i = 1..n) لها شكل قطري إذا وفقط إذا كانت جميع متجهات الأساس عبارة عن متجهات ذاتية للمشغل A.

قاعدة لإيجاد القيم الذاتية والمتجهات الذاتية

. (*)

(1)
أين هي مصفوفة العامل الخطي.

النظام (1) له حل غير صفري إذا كان المحدد D يساوي صفرًا

المثال 12. العامل الخطي A يعمل في R 3 وفقًا للقانون ، حيث x 1 ، x 2 ، .. ، x n هي إحداثيات المتجه في الأساس , , . أوجد القيم الذاتية والمتجهات الذاتية لهذا العامل.
قرار. نبني مصفوفة هذا المشغل:
.
نقوم بتكوين نظام لتحديد إحداثيات المتجهات الذاتية:

نؤلف المعادلة المميزة ونحلها:

.
λ 1،2 = -1 ، λ 3 = 3.
بالتعويض عن λ = -1 في النظام ، لدينا:
أو
مثل ، إذن هناك متغيرين تابعين ومتغير واحد مجاني.
دع x 1 مجاني غير معروف ، إذن نحن نحل هذا النظام بأي طريقة ونجد الحل العام لهذا النظام: يتكون النظام الأساسي للحلول من حل واحد ، حيث أن n - r = 3 - 2 = 1.
مجموعة المتجهات الذاتية المقابلة للقيمة الذاتية λ = -1 لها الشكل: ، حيث x 1 هو أي رقم آخر غير الصفر. دعنا نختار متجهًا واحدًا من هذه المجموعة ، على سبيل المثال ، عن طريق ضبط x 1 = 1: .
بالمثل ، نجد المتجه الذاتي المقابل لقيمة eigenvalue λ = 3: .
في الفضاء R 3 ، يتكون الأساس من ثلاثة نواقل مستقلة خطيًا ، لكننا حصلنا على اثنين فقط من المتجهات الذاتية المستقلة خطيًا ، والتي لا يمكن تشكيل الأساس في R 3. وبالتالي ، لا يمكن اختزال المصفوفة A لمشغل خطي إلى شكل قطري.

المثال 13 معطى مصفوفة .
1. إثبات أن المتجه هو متجه ذاتي للمصفوفة أ. أوجد قيمة eigenvalue المقابلة لهذا المتجه الذاتي.
2. أوجد الأساس الذي تكون فيه المصفوفة أ بشكل قطري.
قرار.
1. إذا ، إذًا هو ناقل eigenvector

.
المتجه (1 ، 8 ، -1) هو متجه ذاتي. القيمة الذاتية λ = -1.
المصفوفة لها شكل قطري في الأساس يتكون من المتجهات الذاتية. واحد منهم مشهور. لنجد الباقي.
نحن نبحث عن المتجهات الذاتية من النظام:

معادلة مميزة: ;
(3 + λ) [- 2 (2-λ) (2 + λ) +3] = 0 ؛ (3 + λ) (λ 2-1) = 0
λ 1 = -3 ، λ 2 = 1 ، λ 3 = -1.
أوجد المتجه الذاتي المقابل للقيمة الذاتية λ = -3:

رتبة مصفوفة هذا النظام تساوي اثنين وتساوي عدد المجهول ، لذلك هذا النظام ليس له سوى حل صفري × 1 = × 3 = 0. × 2 هنا يمكن أن يكون أي شيء آخر غير الصفر ، على سبيل المثال ، س 2 = 1. وبالتالي ، فإن المتجه (0 ، 1.0) هو متجه ذاتي يقابل λ = -3. دعونا تحقق:
.
إذا كانت λ = 1 ، نحصل على النظام
رتبة المصفوفة اثنان. اشطب المعادلة الأخيرة.
دع x 3 يكون المجهول المجاني. ثم x 1 \ u003d -3x 3 ، 4x 2 \ u003d 10x 1-6x 3 \ u003d -30x 3-6x 3 ، x 2 \ u003d -9x 3.
بافتراض x 3 = 1 ، لدينا (-3 ، -9 ، 1) - متجه ذاتي يتوافق مع القيمة الذاتية λ = 1. تحقق من:

.
نظرًا لأن قيم eigenvalues ​​حقيقية ومختلفة ، فإن المتجهات المقابلة لها تكون مستقلة خطيًا ، لذلك يمكن أخذها كأساس في R 3. وهكذا ، في الأساس , , المصفوفة أ لها الشكل:
.
لا يمكن اختزال كل مصفوفة لمشغل خطي A: R n → R n إلى شكل قطري ، لأنه بالنسبة لبعض المشغلين الخطيين قد يكون هناك أقل من n متجهات ذاتية مستقلة خطيًا. ومع ذلك ، إذا كانت المصفوفة متماثلة ، فإن المتجهات المستقلة خطيًا بالضبط تتوافق مع جذر المعادلة المميزة للتعددية م.

تعريف. المصفوفة المتماثلة هي مصفوفة مربعة تتساوى فيها العناصر المتماثلة بالنسبة للقطر الرئيسي ، أي فيها.
ملاحظات. 1. جميع القيم الذاتية لمصفوفة متماثلة حقيقية.
2. المتجهات الذاتية لمصفوفة متماثلة تتوافق مع قيم ذاتية زوجية مختلفة متعامدة.
كواحد من التطبيقات العديدة للجهاز التي تمت دراستها ، فإننا نعتبر مشكلة تحديد شكل منحنى الدرجة الثانية.

التعريف 9.3.المتجه X اتصل ناقل الخاصةالمصفوفات لكنإذا كان هناك مثل هذا الرقم λ, أن المساواة تحمل: لكن X= λ X, وهذا هو نتيجة التقديم على X التحويل الخطي الذي تعطيه المصفوفة لكن، هو ضرب هذا المتجه بالرقم λ . الرقم نفسه λ اتصل رقم خاصالمصفوفات لكن.

الاستبدال في الصيغ (9.3) x` j = λx j ،نحصل على نظام معادلات لتحديد إحداثيات المتجه الذاتي:

. (9.5)

سيكون لهذا النظام المتجانس الخطي حل غير تافه فقط إذا كان المحدد الرئيسي له هو 0 (قاعدة كرامر). بكتابة هذا الشرط في النموذج:

نحصل على معادلة لتحديد القيم الذاتية λ اتصل معادلة مميزة. باختصار ، يمكن تمثيلها على النحو التالي:

| أ- λE | = 0, (9.6)

لأن جانبها الأيسر هو محدد المصفوفة أ- λE. متعدد الحدود فيما يتعلق λ | أ- λE| اتصل كثير الحدود المميزةالمصفوفات أ.

خصائص كثير الحدود المميزة:

1) لا تعتمد كثير الحدود المميز للتحول الخطي على اختيار الأساس. دليل - إثبات. (انظر (9.4)) ، ولكن بالتالي، . وبالتالي ، لا يعتمد على اختيار الأساس. ومن ثم ، و | أ- λE| لا يتغير عند الانتقال إلى أساس جديد.

2) إذا كانت المصفوفة لكنهو التحول الخطي متماثل(هؤلاء. a ij = a ji) ، فإن جميع جذور المعادلة المميزة (9.6) هي أرقام حقيقية.

خصائص القيم الذاتية والمتجهات الذاتية:

1) إذا اخترنا أساسًا من المتجهات الذاتية × 1 ، × 2 ، × 3 المقابلة لقيم eigenvalues λ 1 ، 2 ، 3المصفوفات لكن، إذن على هذا الأساس يكون للتحويل الخطي A مصفوفة قطرية:

(9.7) يأتي إثبات هذه الخاصية من تعريف المتجهات الذاتية.

2) إذا كان التحويل قيم ذاتية لكنمختلفة ، فإن المتجهات الذاتية المقابلة لها تكون مستقلة خطيًا.

3) إذا كانت كثيرة الحدود المميزة للمصفوفة لكنثلاثة جذور مختلفة ، ثم في بعض الأساس المصفوفة لكنله شكل قطري.

دعونا نجد القيم الذاتية والمتجهات الذاتية للمصفوفة ، دعونا نجعل المعادلة المميزة: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0 ، λ 1 = -2, λ 2 = 3, λ 3 = 6.

أوجد إحداثيات المتجهات الذاتية المقابلة لكل قيمة تم العثور عليها λ. من (9.5) يتبع ذلك إذا X (1) ={× 1 ، × 2 ، × 3) هو المتجه الذاتي المقابل ل λ 1 = -2 إذن

هو نظام تعاوني ولكن غير محدد. يمكن كتابة حلها كـ X (1) ={أ,0,-أ) ، حيث a هو أي رقم. على وجه الخصوص ، إذا طلبت ذلك | x (1) |=1, X (1) =

الاستبدال في النظام (9.5) λ 2 = 3 ، نحصل على نظام لتحديد إحداثيات المتجه الذاتي الثاني - x (2) ={y1، y2، y3}:

، أين X (2) ={ب ، -ب ، ب) أو المقدمة | x (2) |=1, x (2) =

ل λ 3 = 6 أوجد المتجه الذاتي x (3) ={z1، z2، z3}:

, x (3) ={ج,2 ج ، ج) أو في النسخة العادية

× (3) = ويمكن أن نرى أن X (1) X (2) = أب- أب= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = قبل الميلاد- 2قبل الميلاد + قبل الميلاد= 0. وهكذا ، فإن المتجهات الذاتية لهذه المصفوفة متعامدة زوجيًا.

المحاضرة 10

الأشكال التربيعية وعلاقتها بالمصفوفات المتماثلة. خصائص المتجهات الذاتية والقيم الذاتية لمصفوفة متماثلة. اختزال الشكل التربيعي إلى الشكل الكنسي.

التعريف 10.1.شكل تربيعيالمتغيرات الحقيقية × 1 ، × 2 ، ... ، × نيسمى كثير الحدود من الدرجة الثانية فيما يتعلق بهذه المتغيرات ، والذي لا يحتوي على مصطلح مجاني وشروط من الدرجة الأولى.

أمثلة على الأشكال التربيعية:

(ن = 2),

(ن = 3). (10.1)

تذكر تعريف المصفوفة المتماثلة الواردة في المحاضرة الأخيرة:

التعريف 10.2.تسمى المصفوفة المربعة متماثل، إذا ، هذا هو ، إذا كانت عناصر المصفوفة متماثلة بالنسبة للقطر الرئيسي متساوية.

خصائص القيم الذاتية والمتجهات الذاتية لمصفوفة متماثلة:

1) جميع القيم الذاتية لمصفوفة متماثلة حقيقية.

إثبات (لـ ن = 2).

دع المصفوفة لكنيشبه: . دعونا نجعل المعادلة المميزة:

(10.2) أوجد المميز:

لذلك ، فإن المعادلة لها جذور حقيقية فقط.

2) المتجهات الذاتية لمصفوفة متماثلة متعامدة.

إثبات (لـ ن= 2).

إحداثيات المتجهات الذاتية ويجب أن تحقق المعادلات.

نظام المعادلات الخطية المتجانسة

نظام المعادلات الخطية المتجانسة هو نظام للصيغة

من الواضح أن في هذه الحالة ، لان جميع عناصر أحد الأعمدة في هذه المحددات تساوي صفرًا.

منذ تم العثور على المجهول بواسطة الصيغ ، ثم في الحالة التي تكون فيها Δ ≠ 0 ، يكون للنظام حل صفري فريد x = ذ = ض= 0. ومع ذلك ، في كثير من المشاكل ، مسألة ما إذا كان النظام المتجانس لديه حلول أخرى غير الصفر هي موضع اهتمام.

نظرية.لكي يكون لنظام المعادلات الخطية المتجانسة حل غير صفري ، من الضروري والكافي أن Δ ≠ 0.

لذلك ، إذا كان المحدد هو Δ ≠ 0 ، فإن النظام لديه حل فريد. إذا كانت Δ ≠ 0 ، فإن نظام المعادلات الخطية المتجانسة يحتوي على عدد لا نهائي من الحلول.

أمثلة.

المتجهات الذاتية والقيم الذاتية للمصفوفة

دعونا نعطي مصفوفة مربعة , Xهو عمود مصفوفة يتطابق ارتفاعه مع ترتيب المصفوفة أ. .

في كثير من المشاكل ، على المرء أن ينظر في معادلة X

أين λ هو رقم ما. من الواضح أنه لأي معادلة λ لها حل صفري.

يتم استدعاء الرقم λ الذي تحتوي هذه المعادلة على حلول غير صفرية القيمة الذاتيةالمصفوفات أ، أ Xلمثل هذا λ يسمى ناقل الخاصةالمصفوفات أ.

لنجد المتجه الذاتي للمصفوفة أ. بقدر ما ه∙س = س، ثم يمكن إعادة كتابة معادلة المصفوفة كـ أو . في الشكل الموسع ، يمكن إعادة كتابة هذه المعادلة كنظام من المعادلات الخطية. هل حقا .

وبالتالي

إذن ، حصلنا على نظام من المعادلات الخطية المتجانسة لتحديد الإحداثيات × 1, x2, × 3المتجه X. لكي يكون للنظام حلول غير صفرية ، من الضروري والكافي أن يكون محدد النظام مساويًا للصفر ، أي

هذه معادلة من الدرجة الثالثة بالنسبة إلى λ. تسمى معادلة مميزةالمصفوفات أويعمل على تحديد القيم الذاتية λ.

كل قيمة ذاتية تتوافق مع ناقل ذاتي X، التي يتم تحديد إحداثياتها من النظام بالقيمة المقابلة لـ.

أمثلة.

ناقل الجبر. مفهوم المتجه

عند دراسة مختلف فروع الفيزياء ، هناك كميات يتم تحديدها تمامًا من خلال تحديد قيمها العددية ، على سبيل المثال ، الطول ، والمساحة ، والكتلة ، ودرجة الحرارة ، إلخ. تسمى هذه القيم العددية. ومع ذلك ، بالإضافة إلى ذلك ، هناك أيضًا كميات لتحديدها ، بالإضافة إلى القيمة العددية ، من الضروري أيضًا معرفة اتجاهها في الفضاء ، على سبيل المثال ، القوة المؤثرة على الجسم والسرعة والتسارع من الجسم عندما يتحرك في الفضاء ، وشدة المجال المغناطيسي في نقطة معينة في الفضاء وما إلى ذلك. تسمى هذه الكميات بالكميات المتجهة.

دعونا نقدم تعريف صارم.

قطعة اتجاهيةدعنا نسمي مقطعًا ، بالنسبة إلى نهاياته المعروف ، أي منهما هو الأول والثاني.

المتجهيسمى المقطع الموجه ، بطول معين ، أي هذا جزء من طول معين ، حيث يتم اعتبار إحدى النقاط المحددة له كبداية ، والثاني - كنهاية. اذا كان أهي بداية المتجه ، بهي نهايتها ، ثم يتم الإشارة إلى المتجه بالرمز ، بالإضافة إلى ذلك ، غالبًا ما يتم الإشارة إلى المتجه بحرف واحد. في الشكل ، يُشار إلى المتجه بمقطع واتجاهه بواسطة سهم.

وحدةأو طويلالمتجه يسمى طول المقطع الموجه الذي يحدده. دلالة عليها || أو ||

سيشار أيضًا إلى ما يسمى بالمتجه الصفري ، الذي تتطابق بدايته مع نهايته ، باسم المتجهات. تم وضع علامة عليه. المتجه الصفري ليس له اتجاه محدد ومعامله يساوي الصفر || = 0.

نواقل وتسمى علاقة خطية متداخلةإذا كانت تقع على نفس الخط أو على خطوط متوازية. في هذه الحالة ، إذا تم توجيه المتجهات بشكل متساوٍ ، فسنكتب بشكل معاكس.

يتم استدعاء المتجهات الموجودة على خطوط مستقيمة موازية لنفس المستوى متحد المستوى.

نواقل اثنين ويسمى مساوإذا كانا متصلين ، ولهما نفس الاتجاه ، ومتساويان في الطول. في هذه الحالة اكتب.

ويترتب على تعريف المساواة في النواقل أنه يمكن تحريك المتجه بالتوازي مع نفسه عن طريق وضع أصله في أي نقطة في الفضاء.

علي سبيل المثال.

العمليات الخطية على المتجهات

1. ضرب متجه برقم.

   حاصل ضرب المتجه برقم λ هو متجه جديد مثل:

   يتم الإشارة إلى حاصل ضرب المتجه والرقم λ بواسطة.

   

   علي سبيل المثال،هو متجه يشير في نفس اتجاه المتجه ويبلغ طوله نصف طول المتجه.

   العملية التي تم إدخالها لها ما يلي ملكيات:

2. إضافة نواقل.

   اسمحوا واثنين من النواقل التعسفية. خذ نقطة اعتباطية اوبناء ناقلات. بعد ذلك ، من النقطة أنضع المتجه جانبا. يسمى المتجه الذي يربط بين بداية المتجه الأول بنهاية الثاني مجموعمن هذه النواقل ويشار إليها .

   

   يسمى التعريف المصاغ لإضافة المتجه حكم متوازي الأضلاع، حيث يمكن الحصول على نفس مجموع النواقل على النحو التالي. نضع جانبا من النقطة اناقلات و. أنشئ متوازي أضلاع على هذه المتجهات OABC. منذ المتجهات ، ثم المتجه ، وهو قطري متوازي الأضلاع المرسوم من الرأس ا، سيكون من الواضح أنه مجموع المتجهات.

   

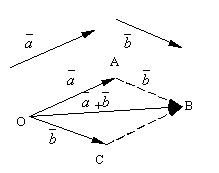
   من السهل التحقق مما يلي ناقلات إضافة خصائص.

3. اختلاف النواقل.

   يسمى المتجه الخطي المتجه إلى متجه معين ، متساوي في الطول وموجه بشكل معاكس ضدمتجه لمتجه ويتم الإشارة إليه بواسطة. يمكن اعتبار المتجه المعاكس نتيجة لضرب المتجه بالرقم λ = –1:.

المتجه الذاتي لمصفوفة مربعة هو الذي ، عند ضربه في مصفوفة معينة ، ينتج عنه متجه خطي. بكلمات بسيطة ، عندما تُضرب المصفوفة في متجه ذاتي ، تظل الأخيرة كما هي ، ولكنها تُضرب في عدد ما.

تعريف

المتجه الذاتي هو متجه غير صفري V ، والذي عند ضربه بمصفوفة مربعة M ، يصبح نفسه ، يزداد بمقدار ما. في التدوين الجبري ، يبدو هذا كما يلي:

م × ف = λ × ف ،

أين λ هي القيمة الذاتية للمصفوفة M.

لنفكر في مثال عددي. لتسهيل الكتابة ، سيتم فصل الأرقام الموجودة في المصفوفة بفاصلة منقوطة. لنفترض أن لدينا مصفوفة:

• م = 0 ؛ 4 ؛
• 6; 10.

دعونا نضربها في متجه العمود:

• الخامس = -2 ؛

عند ضرب مصفوفة في متجه عمود ، نحصل أيضًا على متجه عمود. في لغة رياضية صارمة ، فإن صيغة ضرب مصفوفة 2 × 2 في متجه عمود ستبدو كما يلي:

• M × V = M11 × V11 + M12 × V21 ؛
• M21 × V11 + M22 × V21.

M11 يعني عنصر المصفوفة M ، يقف في الصف الأول والعمود الأول ، و M22 - العنصر الموجود في الصف الثاني والعمود الثاني. بالنسبة للمصفوفة ، هذه العناصر هي M11 = 0 ، M12 = 4 ، M21 = 6 ، M22 10. بالنسبة لمتجه العمود ، هذه القيم هي V11 = –2 ، V21 = 1. وفقًا لهذه الصيغة ، نحصل على ما يلي نتيجة حاصل ضرب مصفوفة مربعة بواسطة متجه:

• M × V = 0 × (-2) + (4) × (1) = 4 ؛
• 6 × (-2) + 10 × (1) = -2.

للراحة ، نكتب متجه العمود في صف واحد. لذلك ، قمنا بضرب المصفوفة المربعة في المتجه (-2 ؛ 1) ، مما نتج عنه المتجه (4 ؛ -2). من الواضح أن هذا هو نفس المتجه مضروبًا في λ = -2. تشير لامدا في هذه الحالة إلى القيمة الذاتية للمصفوفة.

المتجه الذاتي للمصفوفة هو متجه خطي ، أي كائن لا يغير موقعه في الفضاء عندما يتم ضربه في مصفوفة. يشبه مفهوم العلاقة الخطية المتداخلة في الجبر المتجه مصطلح التوازي في الهندسة. في التفسير الهندسي ، المتجهات الخطية هي مقاطع موجهة متوازية ذات أطوال مختلفة. منذ زمن إقليدس ، نعلم أن السطر الواحد يحتوي على عدد لا نهائي من الخطوط الموازية له ، لذلك فمن المنطقي أن نفترض أن كل مصفوفة لها عدد لا حصر له من المتجهات الذاتية.

من المثال السابق ، يمكن ملاحظة أن كلا من (-8 ؛ 4) و (16 ؛ -8) و (32 ، -16) يمكن أن يكونا متجهات ذاتية. كل هذه متجهات خطية تقابل القيمة الذاتية λ = -2. عند ضرب المصفوفة الأصلية في هذه المتجهات ، سنظل نحصل على متجه نتيجة لذلك ، والذي يختلف عن الأصل بمقدار مرتين. هذا هو السبب ، عند حل المشكلات الخاصة بإيجاد ناقل eigenvector ، من الضروري إيجاد كائنات متجهية مستقلة خطيًا فقط. في أغلب الأحيان ، بالنسبة لمصفوفة n × n ، يوجد عدد من المتجهات الذاتية n. تم تصميم الآلة الحاسبة الخاصة بنا لتحليل المصفوفات المربعة من الدرجة الثانية ، لذلك دائمًا ما يتم العثور على متجهين eigenvectors نتيجة لذلك ، إلا عندما يتطابقان.

في المثال أعلاه ، عرفنا مسبقًا المتجه الذاتي للمصفوفة الأصلية وحددنا رقم لامدا بصريًا. ومع ذلك ، من الناحية العملية ، يحدث كل شيء في الاتجاه المعاكس: في البداية توجد قيم eigenvalues ​​وبعد ذلك فقط توجد المتجهات الذاتية.

خوارزمية الحل

لننظر إلى المصفوفة الأصلية M مرة أخرى ونحاول إيجاد متجهيها الذاتيين. لذا تبدو المصفوفة كما يلي:

• م = 0 ؛ 4 ؛
• 6; 10.

بادئ ذي بدء ، نحتاج إلى تحديد القيمة الذاتية λ ، والتي من أجلها نحتاج إلى حساب محدد المصفوفة التالية:

• (0 - λ) ؛ 4 ؛
• 6 ؛ (10 - λ).

يتم الحصول على هذه المصفوفة بطرح المجهول من العناصر الموجودة على القطر الرئيسي. يتم تحديد المحدد بواسطة الصيغة القياسية:

• detA = M11 × M21 - M12 × M22
• detA = (0 - λ) × (10 - λ) - 24

نظرًا لأن المتجه يجب ألا يكون صفراً ، فإننا نأخذ المعادلة الناتجة على أنها تعتمد خطيًا ونساوي المحددات detA بالصفر.

(0 - λ) × (10 - λ) - 24 = 0

لنفتح الأقواس ونحصل على المعادلة المميزة للمصفوفة:

λ 2-10λ - 24 = 0

هذه معادلة تربيعية قياسية تحتاج إلى حل من حيث المميز.

د \ u003d ب 2-4ac \ u003d (-10) × 2-4 × (-1) × 24 \ u003d 100 + 96 \ u003d 196

جذر المميز هو الجذر التربيعي (د) = 14 ، لذا λ1 = -2 ، λ2 = 12. الآن لكل قيمة لامدا ، نحتاج إلى إيجاد المتجه الذاتي. دعونا نعبر عن معاملات النظام لـ λ = -2.

• م - λ × ه = 2 ؛ 4 ؛
• 6; 12.

في هذه الصيغة ، E هي مصفوفة الوحدة. بناءً على المصفوفة التي تم الحصول عليها ، نقوم بتكوين نظام من المعادلات الخطية:

2 س + 4 ص = 6 س + 12 ص

حيث x و y هما عناصر من المتجه الذاتي.

دعونا نجمع كل X على اليسار وكل Y على اليمين. من الواضح - 4x = 8y. قسّم التعبير على - 4 واحصل على x = -2y. الآن يمكننا تحديد المتجه الذاتي الأول للمصفوفة بأخذ أي قيم للمجهول (تذكر ما لا نهاية للمتجهات الذاتية المعتمدة خطيًا). لنأخذ y = 1 ، ثم x = -2. لذلك ، يبدو المتجه الذاتي الأول مثل V1 = (–2 ؛ 1). العودة إلى بداية المقال. لقد كان هذا الكائن المتجه هو الذي ضربنا المصفوفة به لتوضيح مفهوم المتجه الذاتي.

الآن لنجد المتجه الذاتي لـ λ = 12.

• م - λ × E = -12 ؛ 4
• 6; -2.

دعونا نؤلف نفس نظام المعادلات الخطية ؛

• -12 س + 4 ص = 6 س - 2 ص
• -18 س = -6 ص
• 3 س = ص.

الآن لنأخذ x = 1 ، ومن ثم y = 3. وبالتالي ، فإن المتجه الذاتي الثاني يبدو مثل V2 = (1 ؛ 3). عند ضرب المصفوفة الأصلية في هذا المتجه ، ستكون النتيجة دائمًا نفس المتجه مضروبًا في 12. وهذا يكمل خوارزمية الحل. الآن أنت تعرف كيفية تحديد المتجه الذاتي للمصفوفة يدويًا.

• محدد.
• التتبع ، أي مجموع العناصر على القطر الرئيسي ؛
• الترتيب ، أي الحد الأقصى لعدد الصفوف / الأعمدة المستقلة خطيًا.

يعمل البرنامج وفقًا للخوارزمية المذكورة أعلاه ، مما يقلل من عملية الحل. من المهم الإشارة إلى أنه في البرنامج يتم الإشارة إلى لامدا بالحرف "c". لنلقِ نظرة على مثال عددي.

مثال البرنامج

دعنا نحاول تحديد المتجهات الذاتية للمصفوفة التالية:

• م = 5 ؛ ثلاثة عشر؛
• 4; 14.

دعنا ندخل هذه القيم في خلايا الآلة الحاسبة ونحصل على الإجابة بالشكل التالي:

• رتبة المصفوفة: 2 ؛
• محدد المصفوفة: 18 ؛
• تتبع المصفوفة: 19 ؛
• حساب Eigenvector: c 2 - 19.00c + 18.00 (معادلة مميزة) ؛
• حساب Eigenvector: 18 (قيمة لامدا الأولى) ؛
• حساب Eigenvector: 1 (قيمة لامدا الثانية) ؛
• نظام معادلات المتجه 1: -13x1 + 13y1 = 4x1 - 4y1 ؛
• نظام معادلة المتجه 2: 4x1 + 13y1 = 4x1 + 13y1 ؛
• Eigenvector 1: (1 ؛ 1) ؛
• Eigenvector 2: (-3.25 ؛ 1).

وهكذا ، حصلنا على اثنين من المتجهات الذاتية المستقلة خطيًا.

خاتمة

يعد الجبر الخطي والهندسة التحليلية موضوعات قياسية لأي طالب جديد في الهندسة. وجود عدد كبير من المتجهات والمصفوفات أمر مرعب ، ومن السهل ارتكاب خطأ في مثل هذه الحسابات المرهقة. سيسمح برنامجنا للطلاب بالتحقق من حساباتهم أو حل مشكلة العثور على eigenvector تلقائيًا. توجد حاسبات جبر خطية أخرى في الكتالوج الخاص بنا ، استخدمها في دراستك أو عملك.

www.siteيسمح لك أن تجد. الموقع يقوم بالحساب. في غضون ثوانٍ قليلة ، سيعطي الخادم الحل الصحيح. المعادلة المميزة للمصفوفةسيكون تعبيرًا جبريًا تم العثور عليه بواسطة قاعدة حساب المحدد المصفوفات المصفوفات، بينما على القطر الرئيسي ستكون هناك اختلافات في قيم العناصر القطرية والمتغير. عند حساب معادلة مميزة للمصفوفة على الإنترنت، كل عنصر المصفوفاتمع العناصر الأخرى المقابلة المصفوفات. البحث في الوضع عبر الانترنتممكن فقط للمربع المصفوفات. ابحث عن العملية معادلة مميزة للمصفوفة على الإنترنتيقلل من حساب المجموع الجبري لحاصل ضرب العناصر المصفوفاتنتيجة إيجاد المحدد المصفوفات، فقط لغرض التحديد معادلة مميزة للمصفوفة على الإنترنت. تحتل هذه العملية مكانة خاصة في النظرية المصفوفات، يسمح لك بالعثور على قيم eigenvalues ​​والمتجهات باستخدام الجذور. البحث عن المهمة معادلة مميزة للمصفوفة على الإنترنتهو مضاعفة العناصر المصفوفاتمع التجميع اللاحق لهذه المنتجات وفقًا لقاعدة معينة. www.siteيجد معادلة مميزة للمصفوفةبعد معين في الوضع عبر الانترنت. عملية حسابية معادلة مميزة للمصفوفة على الإنترنتبالنسبة لبعد معين ، هذا هو إيجاد كثير الحدود مع معاملات عددية أو رمزية تم العثور عليها بواسطة قاعدة حساب المحدد المصفوفات- كمجموع نواتج العناصر المقابلة المصفوفات، فقط لغرض التحديد معادلة مميزة للمصفوفة على الإنترنت. إيجاد كثير الحدود بالنسبة لمتغير لمربع المصفوفاتكتعريف معادلة مميزة للمصفوفة، شائع من الناحية النظرية المصفوفات. قيمة جذور كثير الحدود معادلة مميزة للمصفوفة على الإنترنتتستخدم لتعريف المتجهات الذاتية والقيم الذاتية لـ المصفوفات. ومع ذلك ، إذا كان المحدد المصفوفاتسيكون صفرا ، إذن معادلة خصائص المصفوفةستظل موجودة ، على عكس العكس المصفوفات. من أجل حساب معادلة مميزة للمصفوفةأو ابحث عن عدة في وقت واحد معادلات مميزة المصفوفات، تحتاج إلى إنفاق الكثير من الوقت والجهد ، بينما سيجد خادمنا معادلة مميزة للمصفوفة على الإنترنت. في هذه الحالة ، الجواب من خلال إيجاد معادلة مميزة للمصفوفة على الإنترنتستكون صحيحة وبدقة كافية ، حتى لو كانت الأرقام عند البحث معادلة مميزة للمصفوفة على الإنترنتسيكون غير عقلاني. متصل www.siteيُسمح بإدخالات الأحرف في العناصر المصفوفات، بمعنى آخر معادلة مميزة للمصفوفة على الإنترنتيمكن تمثيلها بشكل رمزي عام عند الحساب مصفوفة المعادلة المميزة على الإنترنت. من المفيد التحقق من الإجابة التي تم الحصول عليها عند حل مشكلة البحث معادلة مميزة للمصفوفة على الإنترنتباستخدام الموقع www.site. عند إجراء عملية حساب كثير الحدود - المعادلة المميزة للمصفوفة، من الضروري أن تكون منتبهًا ومركّزًا للغاية في حل هذه المشكلة. في المقابل ، سيساعدك موقعنا على التحقق من قرارك بشأن الموضوع مصفوفة المعادلة المميزة على الإنترنت. إذا لم يكن لديك وقت لإجراء فحوصات طويلة للمشكلات التي تم حلها ، فحينئذٍ www.siteسيكون بالتأكيد أداة ملائمة للتحقق عند البحث والحساب معادلة مميزة للمصفوفة على الإنترنت.