Matrisin maksimum öz dəyəri. Matris xarakteristikası tənliyi

Diaqonal tipli matrislər ən sadə şəkildə düzülür. Sual yaranır ki, xətti operatorun matrisinin diaqonal formasına malik olacağı əsas tapmaq mümkündürmü? Belə bir əsas var.
R n xətti fəzası və ona təsir edən A xətti operatoru verilsin; bu halda A operatoru R n-i özünə götürür, yəni A:R n → R n .

Tərif. Sıfırdan fərqli vektor, A operatoru ona kollinear vektora çevrilirsə, A operatorunun xüsusi vektoru adlanır, yəni. λ ədədi xüsusi vektora uyğun gələn A operatorunun xüsusi dəyəri və ya xüsusi dəyəri adlanır.
Şəxsi dəyərlərin və xüsusi vektorların bəzi xüsusiyyətlərini qeyd edirik.
1. Şəxsi vektorların istənilən xətti kombinasiyası operatorunun eyni λ xüsusi qiymətinə uyğun olan A operatorunun eyni xüsusi dəyəri olan xüsusi vektordur.
2. Xüsusi vektorlar λ 1 , λ 2 , …, λ m cüt-cüt fərqli xüsusi qiymətli operator A xətti müstəqildir.
3. Əgər xüsusi qiymətlər λ 1 =λ 2 = λ m = λ olarsa, onda λ xasiyyəti m-dən çox olmayan xətti müstəqil xüsusi vektorlara uyğun gəlir.

Beləliklə, n xətti müstəqil xüsusi vektor olarsa müxtəlif xüsusi qiymətlərə λ 1 , λ 2 , …, λ n uyğun gəlir, onda onlar xətti müstəqildirlər, buna görə də R n fəzasının əsası kimi götürülə bilərlər. Xətti operator A-nın öz vektorları əsasında matrisinin formasını tapaq, bunun üçün A operatoru ilə əsas vektorlar əsasında hərəkət edirik: sonra .
Beləliklə, A xətti operatorunun öz vektorları əsasında matrisi diaqonal formaya malikdir və A operatorunun xüsusi qiymətləri diaqonaldadır.
Matrisin diaqonal forması olan başqa əsas varmı? Bu sualın cavabı aşağıdakı teoremlə verilir.

teorem. Bazadakı (i = 1..n) xətti operatorun matrisi o halda diaqonal formaya malikdir, o halda ki, bazisin bütün vektorları A operatorunun xüsusi vektorları olsun.

Şəxsi dəyərlərin və xüsusi vektorların tapılması qaydası

. (*)

(1)
harada xətti operatorun matrisidir.

Sistemin (1) determinantı D sıfıra bərabərdirsə, onun sıfırdan fərqli həlli var

Misal 12. X 1 , x 2 , .., x n əsasdakı vektorun koordinatları olan A xətti operatoru R 3-də qanuna uyğun olaraq fəaliyyət göstərir . , , . Bu operatorun xüsusi qiymətlərini və xüsusi vektorlarını tapın.
Qərar. Bu operatorun matrisini qururuq:
.
Xüsusi vektorların koordinatlarını təyin etmək üçün bir sistem tərtib edirik:

Xarakterik tənliyi qururuq və həll edirik:

.
λ 1,2 = -1, λ 3 = 3.
Sistemdə λ = -1 əvəz etsək, əldə edirik:
və ya
kimi , onda iki asılı dəyişən və bir sərbəst dəyişən var.
O zaman x 1 sərbəst naməlum olsun Bu sistemi istənilən yolla həll edirik və bu sistemin ümumi həllini tapırıq: Əsas həllər sistemi bir həlldən ibarətdir, çünki n - r = 3 - 2 = 1.
λ = -1 xüsusi dəyərinə uyğun gələn xüsusi vektorlar çoxluğu formaya malikdir: , burada x 1 sıfırdan başqa istənilən ədəddir. Bu dəstdən bir vektor seçək, məsələn, x 1 = 1 təyin edərək: .
Oxşar şəkildə mübahisə edərək, λ = 3 xüsusi dəyərə uyğun olan xüsusi vektoru tapırıq: .
R 3 fəzasında bazis üç xətti müstəqil vektordan ibarətdir, lakin biz yalnız iki xətti müstəqil xüsusi vektor əldə etdik ki, onlardan R 3-də bazis yaratmaq mümkün deyil. Nəticə etibarı ilə xətti operatorun A matrisi diaqonal formaya endirilə bilməz.

Misal 13 Bir matris verilmişdir .
1. vektor olduğunu sübut edin A matrisinin xüsusi vektorudur. Bu xüsusi vektora uyğun olan xüsusi dəyəri tapın.
2. A matrisinin diaqonal formasına malik olduğu əsası tapın.
Qərar.
1. Əgər , onda xüsusi vektordur

.
Vektor (1, 8, -1) xüsusi vektordur. Xüsusi dəyər λ = -1.
Matris əsasda xüsusi vektorlardan ibarət diaqonal formaya malikdir. Onlardan biri məşhurdur. Qalanını tapaq.
Sistemdən öz vektorları axtarırıq:

Xarakterik tənlik: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
λ = -3 xüsusi dəyərinə uyğun olan xüsusi vektoru tapın:

Bu sistemin matrisinin dərəcəsi ikiyə bərabərdir və naməlumların sayına bərabərdir, ona görə də bu sistemin yalnız sıfır həlli var x 1 = x 3 = 0. Burada x 2 sıfırdan başqa hər şey ola bilər, məsələn, x 2 = 1. Beləliklə, vektor (0 ,1,0) λ = -3-ə uyğun olan xüsusi vektordur. yoxlayaq:
.
Əgər λ = 1 olarsa, sistemi alırıq
Matrisin dərəcəsi ikidir. Son tənliyi kəsin.
X 3 sərbəst naməlum olsun. Sonra x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
x 3 = 1 fərz etsək, (-3,-9,1) - λ = 1 xüsusi dəyərinə uyğun olan xüsusi vektor var. Yoxlayın:

.
Şəxsi dəyərlər həqiqi və fərqli olduğundan, onlara uyğun gələn vektorlar xətti müstəqildir, buna görə də R 3-də əsas götürülə bilər. Beləliklə, əsasda , , A matrisinin forması var:
.
A:R n → R n xətti operatorunun hər bir matrisi diaqonal formaya endirilə bilməz, çünki bəzi xətti operatorlar üçün n-dən az xətti müstəqil xüsusi vektor ola bilər. Bununla belə, əgər matris simmetrikdirsə, onda m xətti müstəqil vektor çoxluğun xarakterik tənliyinin kökünə uyğun gəlir.

Tərif. Simmetrik matris, əsas diaqonala görə simmetrik olan elementlərin bərabər olduğu kvadrat matrisdir, yəni .
Qeydlər. 1. Simmetrik matrisin bütün xüsusi qiymətləri həqiqidir.
2. Cütləşmiş müxtəlif xüsusi qiymətlərə uyğun gələn simmetrik matrisin məxsusi vektorları ortoqonaldır.
Tədqiq olunan aparatın çoxsaylı tətbiqlərindən biri kimi biz ikinci dərəcəli əyrinin formasının təyini problemini nəzərdən keçiririk.

Tərif 9.3. Vektor X çağırdı öz vektoru matrislər AMMA belə bir nömrə varsa λ, bərabərlik təmin edir: AMMA X= λ X, yəni müraciətin nəticəsidir X matris tərəfindən verilən xətti çevrilmə AMMA, bu vektorun ədədə vurulmasıdır λ . Nömrənin özü λ çağırdı öz nömrəsi matrislər AMMA.

Düsturlara əvəz edilməsi (9.3) x` j = λx j, xüsusi vektorun koordinatlarını təyin etmək üçün tənliklər sistemini alırıq:

. (9.5)

Bu xətti homojen sistemin qeyri-trivial həlli yalnız onun əsas determinantı 0 olarsa (Kramer qaydası) olacaqdır. Bu şərti formada yazmaqla:

xüsusi qiymətləri təyin etmək üçün tənlik alırıq λ çağırdı xarakterik tənlik. Qısaca onu aşağıdakı kimi təqdim etmək olar:

| A-λE | = 0, (9.6)

çünki onun sol tərəfi matrisin determinantıdır A-λE. ilə bağlı çoxhədli λ | A-λE| çağırdı xarakterik polinom matrislər A.

Xarakterik polinomun xassələri:

1) Xətti çevrilmənin xarakterik polinomu bazisin seçilməsindən asılı deyil. Sübut. (bax (9.4)), lakin deməli, . Beləliklə, əsas seçimindən asılı deyil. Beləliklə, və | A-λE| yeni əsasa keçid zamanı dəyişmir.

2) Əgər matris AMMA xətti çevrilmədir simmetrik(onlar. a ij = a ji), onda (9.6) xarakterik tənliyin bütün kökləri həqiqi ədədlərdir.

Xüsusi dəyərlərin və xüsusi vektorların xüsusiyyətləri:

1) Xüsusi vektorlardan bazis seçsək x 1, x 2, x 3 xüsusi qiymətlərə uyğundur λ 1 , λ 2 , λ 3 matrislər AMMA, onda bu əsasda xətti çevrilmə A diaqonal matrisə malikdir:

(9.7) Bu xüsusiyyətin sübutu xüsusi vektorların tərifindən irəli gəlir.

2) Əgər çevrilmə xüsusi qiymətlərdirsə AMMA fərqlidirlər, onda onlara uyğun gələn xüsusi vektorlar xətti müstəqildir.

3) Əgər matrisin xarakterik polinomu AMMAüç fərqli kökə malikdir, sonra hansısa əsasda matris AMMA diaqonal formaya malikdir.

Matrisin xüsusi qiymətlərini və xüsusi vektorlarını tapaq Xarakterik tənliyi quraq: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Tapılan hər bir qiymətə uyğun olan xüsusi vektorların koordinatlarını tapın λ. (9.5)-dən belə çıxır ki, əgər X (1) ={x 1 , x 2 , x 3) uyğun olan xüsusi vektordur λ 1 = -2, onda

əməkdaşlıq, lakin qeyri-müəyyən bir sistemdir. Onun həlli kimi yazmaq olar X (1) ={a,0,-a), burada a istənilən ədəddir. Xüsusilə, bunu tələb edirsinizsə | x (1) |=1, X (1) =

Sistemə daxil edilməsi (9.5) λ 2 =3, ikinci xüsusi vektorun koordinatlarını təyin etmək üçün bir sistem alırıq - x (2) ={y1,y2,y3}:

, harada X (2) ={b,-b,b) və ya təmin | x (2) |=1, x (2) =

üçün λ 3 = 6 xüsusi vektoru tapın x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) və ya normallaşdırılmış versiyada

x (3) = Bunu görmək olar X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = e.ə- 2bc + e.ə= 0. Beləliklə, bu matrisin xüsusi vektorları qoşa ortoqonaldır.

Mühazirə 10

Kvadrat formalar və onların simmetrik matrislərlə əlaqəsi. Simmetrik matrisin xüsusi vektorlarının və xüsusi qiymətlərinin xassələri. Kvadrat formanın kanonik formaya salınması.

Tərif 10.1.kvadrat forma real dəyişənlər x 1, x 2,…, x n bu dəyişənlərə münasibətdə ikinci dərəcəli çoxhədli deyilir ki, tərkibində sərbəst termin və birinci dərəcəli hədlər yoxdur.

Kvadrat formaların nümunələri:

(n = 2),

(n = 3). (10.1)

Son mühazirədə verilən simmetrik matrisin tərifini xatırlayın:

Tərif 10.2. Kvadrat matrisa deyilir simmetrik, əgər , yəni əsas diaqonala görə simmetrik olan matrisin elementləri bərabərdirsə.

Simmetrik matrisin xüsusi qiymətlərinin və xüsusi vektorlarının xassələri:

1) Simmetrik matrisin bütün xüsusi qiymətləri həqiqidir.

Sübut (üçün n = 2).

Matris olsun AMMA oxşayır: . Xarakterik tənliyi yaradaq:

(10.2) Diskriminantı tapın:

Buna görə də tənliyin yalnız həqiqi kökləri var.

2) Simmetrik matrisin məxsusi vektorları ortoqonaldır.

Sübut (üçün n= 2).

Xüsusi vektorların koordinatları və tənlikləri təmin etməlidir.

HOMogen Xətti TƏNLƏR SİSTEMİ

Homojen xətti tənliklər sistemi forma sistemidir

Aydındır ki, bu halda , çünki bu təyinedicilərdəki sütunlardan birinin bütün elementləri sıfıra bərabərdir.

Çünki naməlumlar düsturlarla tapılır , onda Δ ≠ 0 olduqda, sistemin unikal sıfır həlli var x = y = z= 0. Lakin bir çox məsələlərdə homojen sistemin sıfırdan başqa həllərin olub-olmaması sualı maraq doğurur.

teorem. Xətti homojen tənliklər sisteminin sıfırdan fərqli həlli üçün Δ ≠ 0 olması zəruri və kifayətdir.

Deməli, determinant Δ ≠ 0 olarsa, sistemin unikal həlli var. Əgər Δ ≠ 0 olarsa, onda xətti bircins tənliklər sisteminin sonsuz sayda həlli var.

Nümunələr.

Xüsusi vektorlar və matrisin xüsusi qiymətləri

Kvadrat matris verilsin , X hündürlüyü matrisin sırası ilə üst-üstə düşən bəzi matris-sütundur A. .

Bir çox problemdə tənliyi nəzərə almaq lazımdır X

burada λ hansısa ədəddir. Aydındır ki, istənilən λ üçün bu tənliyin sıfır həlli var.

Bu tənliyin sıfırdan fərqli həlli olduğu λ ədədi adlanır xüsusi dəyər matrislər A, a X belə λ adlanır öz vektoru matrislər A.

Matrisin xüsusi vektorunu tapaq A. kimi E∙X=X, onda matris tənliyi kimi yenidən yazıla bilər və ya . Genişləndirilmiş formada bu tənlik xətti tənliklər sistemi kimi yenidən yazıla bilər. Həqiqətən .

Və buna görə də

Beləliklə, koordinatları təyin etmək üçün homojen xətti tənliklər sistemi əldə etdik x 1, x2, x 3 vektor X. Sistemin sıfırdan fərqli həlləri olması üçün sistemin determinantının sıfıra bərabər olması zəruri və kifayətdir, yəni.

Bu λ ilə əlaqədar 3-cü dərəcəli tənlikdir. Bu adlanır xarakterik tənlik matrislər A və λ xüsusi qiymətlərini təyin etməyə xidmət edir.

Hər bir xüsusi dəyər λ bir xüsusi vektora uyğundur X, onun koordinatları sistemdən müvafiq λ qiymətində müəyyən edilir.

Nümunələr.

VEKTOR CƏBRİ. VEKTOR KONSEPT

Fizikanın müxtəlif sahələrini öyrənərkən onların ədədi qiymətlərini təyin etməklə tamamilə müəyyən edilən kəmiyyətlər, məsələn, uzunluq, sahə, kütlə, temperatur və s. Belə dəyərlərə skalyar deyilir. Bununla belə, bunlara əlavə olaraq, kəmiyyətlər də var ki, onları müəyyən etmək üçün ədədi qiymətdən əlavə, kosmosda istiqamətini də bilmək lazımdır, məsələn, bədənə təsir edən qüvvə, sürət və sürətlənmə. kosmosda hərəkət edərkən cismin, kosmosun müəyyən bir nöqtəsində maqnit sahəsinin gücü və s. Belə kəmiyyətlərə vektor kəmiyyətlər deyilir.

Gəlin ciddi bir tərif təqdim edək.

İstiqamətli seqment Uclarına nisbətən hansının birinci, hansının ikinci olduğu məlum olan seqmenti adlandıraq.

Vektor müəyyən uzunluğa malik yönəldilmiş seqment deyilir, yəni. Bu, müəyyən bir uzunluqda bir seqmentdir, burada onu məhdudlaşdıran nöqtələrdən biri başlanğıc, ikincisi isə son kimi qəbul edilir. Əgər a A vektorun başlanğıcıdır, B onun sonudur, onda vektor simvolu ilə işarələnir, əlavə olaraq, vektor çox vaxt tək hərflə işarələnir. Şəkildə vektor seqmentlə, istiqaməti isə oxla göstərilir.

modul və ya uzun vektor onu təyin edən istiqamətlənmiş seqmentin uzunluğu adlanır. || ilə işarələnir və ya ||.

Əvvəli və sonu üst-üstə düşən sıfır vektoru da vektor adlandırılacaq. İşarələnmişdir. Sıfır vektorunun müəyyən istiqaməti yoxdur və onun modulu sıfıra bərabərdir ||=0.

Vektorlar və adlanır kollinear eyni xəttdə və ya paralel xətlər üzərində yerləşdikdə. Bu halda və vektorları bərabər istiqamətləndirilirsə, əksini yazacağıq.

Eyni müstəviyə paralel düz xətlər üzərində yerləşən vektorlara deyilir düzbucaqlı.

İki vektor və adlanır bərabərdirəgər onlar kollineardırsa, eyni istiqamətə malikdirlər və uzunluqları bərabərdirlər. Bu vəziyyətdə yazın.

Vektorların bərabərliyinin tərifindən belə çıxır ki, vektor kosmosun istənilən nöqtəsində başlanğıcını yerləşdirməklə özünə paralel hərəkət edə bilər.

misal üçün.

VEKTORLAR ÜZRƏ XƏTİ ƏMƏLƏLƏR

1. Bir vektorun ədədə vurulması.

   Vektorun λ ədədinin hasili yeni vektordur, belə ki:

   Vektor və λ ədədinin hasili ilə işarələnir.

   

   Misal üçün, vektorla eyni istiqaməti göstərən və vektorun uzunluğunun yarısı olan vektordur.

   Daxil edilmiş əməliyyat aşağıdakılara malikdir xassələri:

2. Vektorların əlavə edilməsi.

   Qoy və iki ixtiyari vektor olsun. İxtiyari bir nöqtə götürün O və vektor qurun. Bundan sonra, nöqtədən A vektoru kənara qoyun. Birinci vektorun əvvəlini ikincinin sonu ilə birləşdirən vektor deyilir məbləğ bu vektorların və işarələnir .

   

   Vektor əlavəsinin tərtib edilmiş tərifi adlanır paraleloqram qaydası, çünki vektorların eyni cəmini aşağıdakı kimi almaq olar. Nöqtədən kənara qoyun O vektorlar və . Bu vektorlar üzərində paraleloqram qurun OABC. Çünki vektorlar , sonra təpədən çəkilmiş paraleloqramın diaqonalı olan vektor O, açıq-aydın vektorların cəmi olacaq.

   

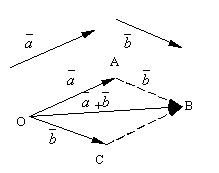
   Aşağıdakıları yoxlamaq asandır vektor əlavə xassələri.

3. Vektorların fərqi.

   Verilmiş vektora uyğun uzunluğa bərabər və əks istiqamətdə olan vektor deyilir əks vektor üçün vektor və ilə işarələnir. Əks vektor vektorun λ = –1 ədədinə vurulmasının nəticəsi hesab edilə bilər: .

Kvadrat matrisin öz vektoru odur ki, verilmiş matrislə vurulduqda kollinear vektor yaranır. Sadə sözlə desək, bir matris öz vektoru ilə vurulduqda, sonuncu eyni qalır, lakin bəzi ədədə vurulur.

Tərif

Öz vektor sıfırdan fərqli V vektordur, M kvadrat matrisə vurulduqda özünə çevrilir, müəyyən λ ədədi ilə artır. Cəbri notasiyada bu belə görünür:

M × V = λ × V,

burada λ M matrisinin xüsusi dəyəridir.

Rəqəmsal bir misala baxaq. Yazının rahatlığı üçün matrisdəki nömrələr nöqtəli vergüllə ayrılacaq. Tutaq ki, bizim bir matrisimiz var:

• M = 0; 4;
• 6; 10.

Onu sütun vektoruna vuraq:

• V = -2;

Bir matrisi sütun vektoruna vurduqda, biz də sütun vektoru alırıq. Ciddi riyazi dildə, 2 × 2 matrisi sütun vektoruna vurmaq üçün düstur belə görünür:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 birinci cərgədə və birinci sütunda duran M matrisinin elementini, M22 isə ikinci sətirdə və ikinci sütunda yerləşən elementi bildirir. Matrisimiz üçün bu elementlər M11 = 0, M12 = 4, M21 = 6, M22 10-dur. Sütun vektoru üçün bu dəyərlər V11 = –2, V21 = 1-dir. Bu düstura görə aşağıdakıları alırıq. kvadrat matrisin vektorla hasilinin nəticəsi:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Rahatlıq üçün sütun vektorunu bir sıraya yazırıq. Beləliklə, kvadrat matrisi vektora (-2; 1) vurduq, nəticədə (4; -2) vektoru əldə etdik. Aydındır ki, bu λ = -2 ilə vurulan eyni vektordur. Lambda bu halda matrisin öz dəyərini bildirir.

Bir matrisin özünəməxsus vektoru kollinear vektordur, yəni matrislə vurulduqda fəzada öz mövqeyini dəyişməyən obyektdir. Vektor cəbrində kollinearlıq anlayışı həndəsədəki paralellik termininə bənzəyir. Həndəsi şərhdə kollinear vektorlar müxtəlif uzunluqlu paralel istiqamətlənmiş seqmentlərdir. Evklid dövründən bəri biz bilirik ki, tək bir xəttin ona paralel sonsuz sayda xətləri var, ona görə də hər bir matrisin sonsuz sayda öz vektoru olduğunu düşünmək məntiqlidir.

Əvvəlki nümunədən görmək olar ki, həm (-8; 4), həm də (16; -8) və (32, -16) öz vektor ola bilər. Bütün bunlar λ = -2 xüsusi qiymətə uyğun gələn kollinear vektorlardır. Orijinal matrisi bu vektorlara vurduqda biz yenə də nəticədə orijinaldan 2 dəfə fərqlənən vektor alacağıq. Məhz buna görə də məxsi vektoru tapmaq üçün məsələləri həll edərkən yalnız xətti müstəqil vektor obyektlərini tapmaq tələb olunur. Çox vaxt n × n matrisi üçün n-ci sayda xüsusi vektorlar olur. Kalkulyatorumuz ikinci dərəcəli kvadrat matrislərin təhlili üçün nəzərdə tutulmuşdur, ona görə də, üst-üstə düşdüyü hallar istisna olmaqla, nəticədə demək olar ki, həmişə iki məxsusi vektor tapılacaqdır.

Yuxarıdakı misalda biz əvvəlcədən orijinal matrisin öz vektorunu bilirdik və lambda sayını vizual olaraq təyin etdik. Bununla belə, praktikada hər şey tərsinə baş verir: başlanğıcda xüsusi qiymətlər və yalnız bundan sonra xüsusi vektorlar var.

Həll alqoritmi

Orijinal M matrisinə yenidən baxaq və onun hər iki məxsus vektorunu tapmağa çalışaq. Beləliklə, matris belə görünür:

• M = 0; 4;
• 6; 10.

Başlamaq üçün, λ xüsusi dəyərini təyin etməliyik, bunun üçün aşağıdakı matrisin determinantını hesablamalıyıq:

• (0 − λ); 4;
• 6; (10 − λ).

Bu matris əsas diaqonaldakı elementlərdən naməlum λ çıxılmaqla əldə edilir. Determinant standart düsturla müəyyən edilir:

• detA = M11 × M21 - M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Vektorumuz sıfır olmamalıdır, nəticədə yaranan tənliyi xətti asılı olaraq qəbul edirik və determinantımızı detA-nı sıfıra bərabərləşdiririk.

(0 − λ) × (10 − λ) − 24 = 0

Mötərizələri açaq və matrisin xarakterik tənliyini əldə edək:

λ 2 − 10λ − 24 = 0

Bu, diskriminant baxımından həll edilməli olan standart kvadrat tənlikdir.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Diskriminantın kökü sqrt(D) = 14-dür, ona görə də λ1 = -2, λ2 = 12. İndi hər bir lambda dəyəri üçün biz xüsusi vektor tapmalıyıq. λ = -2 üçün sistemin əmsallarını ifadə edək.

• M − λ × E = 2; 4;
• 6; 12.

Bu düsturda E eynilik matrisidir. Alınan matrisə əsasən xətti tənliklər sistemini tərtib edirik:

2x + 4y = 6x + 12y

burada x və y xüsusi vektorun elementləridir.

Soldakı bütün X-ləri və sağdakı bütün Y-ləri toplayaq. Aydındır ki, - 4x = 8y. İfadəni - 4-ə bölün və x = -2y alın. İndi naməlumların istənilən qiymətini götürərək matrisin birinci xüsusi vektorunu təyin edə bilərik (xətti asılı olan xüsusi vektorların sonsuzluğunu xatırlayın). y = 1 götürək, onda x = -2. Buna görə də birinci xüsusi vektor V1 = (–2; 1) kimi görünür. Məqalənin əvvəlinə qayıdın. Məhz bu vektor obyekti idi ki, biz xüsusi vektor anlayışını nümayiş etdirmək üçün matrisi çoxaldıq.

İndi λ = 12 üçün məxsusi vektoru tapaq.

• M - λ × E = -12; 4
• 6; -2.

Eyni xətti tənliklər sistemini tərtib edək;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x=y.

İndi x = 1 götürək, deməli, y = 3. Beləliklə, ikinci xüsusi vektor V2 = (1; 3) kimi görünür. Orijinal matrisi bu vektora vurduqda, nəticə həmişə eyni vektorun 12-yə vurulması olacaq. Bu, həll alqoritmini tamamlayır. İndi siz matrisin öz vektorunu əl ilə necə təyin edəcəyinizi bilirsiniz.

• təyinedici;
• iz, yəni əsas diaqonaldakı elementlərin cəmi;
• dərəcə, yəni xətti müstəqil sətirlərin/sütunların maksimum sayı.

Proqram həll prosesini minimuma endirərək yuxarıda göstərilən alqoritmə uyğun işləyir. Qeyd etmək lazımdır ki, proqramda lambda "c" hərfi ilə işarələnir. Rəqəmsal bir nümunəyə baxaq.

Proqram nümunəsi

Aşağıdakı matris üçün xüsusi vektorları təyin etməyə çalışaq:

• M=5; on üç;
• 4; 14.

Gəlin bu dəyərləri kalkulyatorun xanalarına daxil edək və cavabı aşağıdakı formada alaq:

• Matris dərəcəsi: 2;
• Matris təyinedicisi: 18;
• Matris izi: 19;
• Özvektorun hesablanması: c 2 − 19.00c + 18.00 (xarakteristik tənlik);
• Özvektorun hesablanması: 18 (birinci lambda dəyəri);
• Özvektorun hesablanması: 1 (ikinci lambda dəyəri);
• 1-ci vektorun tənliklər sistemi: -13x1 + 13y1 = 4x1 − 4y1;
• Vektor 2 tənlik sistemi: 4x1 + 13y1 = 4x1 + 13y1;
• Xüsusi vektor 1: (1; 1);
• Xüsusi vektor 2: (-3,25; 1).

Beləliklə, iki xətti müstəqil xüsusi vektor əldə etdik.

Nəticə

Xətti cəbr və analitik həndəsə mühəndislik üzrə istənilən birinci kurs tələbəsi üçün standart fənlərdir. Çoxlu sayda vektor və matrislər dəhşətlidir və belə çətin hesablamalarda səhv etmək asandır. Proqramımız tələbələrə öz hesablamalarını yoxlamağa və ya öz vektoru tapmaq məsələsini avtomatik həll etməyə imkan verəcək. Kataloqumuzda başqa xətti cəbr kalkulyatorları var, onlardan dərsinizdə və ya işinizdə istifadə edin.

www.site tapmağa imkan verir. Sayt hesablama aparır. Bir neçə saniyədən sonra server düzgün həlli verəcəkdir. Matris üçün xarakterik tənlik determinantın hesablanması qaydası ilə tapılan cəbri ifadə olacaq matrislər matrislər, əsas diaqonalda isə diaqonal elementlərin və dəyişənin dəyərlərində fərqlər olacaq. Hesablayarkən matris üçün xarakterik tənlik online, hər bir element matrislər müvafiq digər elementlərlə vurulacaq matrislər. Rejimdə tapın onlayn yalnız kvadrat üçün mümkündür matrislər. Əməliyyatı tapın matris üçün xarakterik tənlik online elementlərin hasilinin cəbri cəminin hesablanmasına qədər azaldır matrislər təyinedicinin tapılması nəticəsində matrislər, yalnız müəyyən etmək məqsədi ilə matris üçün xarakterik tənlik online. Bu əməliyyat nəzəriyyədə xüsusi yer tutur matrislər, köklərdən istifadə edərək öz dəyərləri və vektorları tapmağa imkan verir. Tapşırıq tapşırığı matris üçün xarakterik tənlik online elementləri çoxaltmaqdır matrislər müəyyən bir qaydaya uyğun olaraq bu məhsulların sonrakı cəmlənməsi ilə. www.site tapır matris üçün xarakterik tənlik rejimdə verilmiş ölçü onlayn. hesablama matris üçün xarakterik tənlik online verilmiş ölçü üçün bu, determinantın hesablanması qaydası ilə tapılan ədədi və ya simvolik əmsalları olan çoxhədli tapmaqdır. matrislər- müvafiq elementlərin məhsullarının cəmi kimi matrislər, yalnız müəyyən etmək məqsədi ilə matris üçün xarakterik tənlik online. Kvadrat üçün dəyişənə görə çoxhədlinin tapılması matrislər, tərif kimi matris üçün xarakterik tənlik, nəzəri cəhətdən ümumi matrislər. Çoxhədlinin köklərinin qiyməti matris üçün xarakterik tənlik onlineüçün xüsusi vektorları və xüsusi dəyərləri müəyyən etmək üçün istifadə olunur matrislər. Ancaq determinant olarsa matrislər onda sıfır olacaq matris xarakteristikası tənliyiəksindən fərqli olaraq hələ də mövcud olacaq matrislər. Hesablamaq üçün matris üçün xarakterik tənlik və ya eyni anda bir neçə axtarın matrislərin xarakterik tənlikləri, çox vaxt və səy sərf etməli, serverimiz tapacaq onlayn matris üçün xarakterik tənlik. Bu vəziyyətdə cavab tapmaqla matris üçün xarakterik tənlik onlineədədləri taparkən belə düzgün və kifayət qədər dəqiqliklə olacaq matris üçün xarakterik tənlik online irrasional olacaq. Onlayn www.site elementlərdə simvol girişlərinə icazə verilir matrislər, yəni onlayn matris üçün xarakterik tənlik hesablanarkən ümumi simvolik formada təmsil oluna bilər xarakterik tənlik matrisi online. Tapma məsələsini həll edərkən alınan cavabı yoxlamaq faydalıdır matris üçün xarakterik tənlik online saytdan istifadə etməklə www.site. Polinomun hesablanması əməliyyatını yerinə yetirərkən - matrisin xarakterik tənliyi, bu problemin həllində diqqətli və son dərəcə diqqətli olmaq lazımdır. Öz növbəsində saytımız mövzu ilə bağlı qərarınızı yoxlamaqda sizə kömək edəcək xarakterik tənlik matrisi online. Əgər həll olunan problemlərin uzun müddət yoxlanılmasına vaxtınız yoxdursa, o zaman www.site tapmaq və hesablamaq üçün əlbəttə ki, yoxlamaq üçün əlverişli bir vasitədir matris üçün xarakterik tənlik online.