Operatorun öz qiymətlərini tapın. Xüsusi qiymətlər (ədədlər) və xüsusi vektorlar Həll nümunələri

Diaqonal tipli matrislər ən sadə şəkildə düzülür. Sual yaranır ki, xətti operatorun matrisinin diaqonal formasına malik olacağı əsas tapmaq mümkündürmü? Belə bir əsas var.
R n xətti fəzası və ona təsir edən A xətti operatoru verilsin; bu halda A operatoru R n-i özünə götürür, yəni A:R n → R n .

Tərif. Sıfırdan fərqli vektor, A operatoru ona kollinear vektora çevrilirsə, A operatorunun xüsusi vektoru adlanır, yəni. λ ədədi xüsusi vektora uyğun gələn A operatorunun xüsusi dəyəri və ya xüsusi dəyəri adlanır.
Şəxsi dəyərlərin və xüsusi vektorların bəzi xüsusiyyətlərini qeyd edirik.
1. Şəxsi vektorların istənilən xətti kombinasiyası operatorunun eyni λ xüsusi qiymətinə uyğun olan A operatorunun eyni xüsusi dəyəri olan xüsusi vektordur.
2. Xüsusi vektorlar λ 1 , λ 2 , …, λ m cüt-cüt fərqli xüsusi qiymətli operator A xətti müstəqildir.
3. Əgər xüsusi qiymətlər λ 1 =λ 2 = λ m = λ olarsa, onda λ xasiyyəti m-dən çox olmayan xətti müstəqil xüsusi vektorlara uyğun gəlir.

Beləliklə, n xətti müstəqil xüsusi vektor olarsa müxtəlif xüsusi qiymətlərə λ 1 , λ 2 , …, λ n uyğun gəlir, onda onlar xətti müstəqildirlər, buna görə də R n fəzasının əsası kimi götürülə bilərlər. Xətti operator A-nın öz vektorları əsasında matrisinin formasını tapaq, bunun üçün A operatoru ilə əsas vektorlar əsasında hərəkət edirik: sonra .
Beləliklə, A xətti operatorunun öz vektorları əsasında matrisi diaqonal formaya malikdir və A operatorunun xüsusi qiymətləri diaqonaldadır.
Matrisin diaqonal forması olan başqa əsas varmı? Bu sualın cavabı aşağıdakı teoremlə verilir.

teorem. Bazadakı (i = 1..n) xətti operatorun matrisi o halda diaqonal formaya malikdir, o halda ki, bazisin bütün vektorları A operatorunun xüsusi vektorları olsun.

Şəxsi dəyərlərin və xüsusi vektorların tapılması qaydası

. (*)

(1)
harada xətti operatorun matrisidir.

Sistemin (1) determinantı D sıfıra bərabərdirsə, onun sıfırdan fərqli həlli var

Misal 12. X 1 , x 2 , .., x n əsasdakı vektorun koordinatları olan A xətti operatoru R 3-də qanuna uyğun olaraq fəaliyyət göstərir . , , . Bu operatorun xüsusi qiymətlərini və xüsusi vektorlarını tapın.
Qərar. Bu operatorun matrisini qururuq:
.
Xüsusi vektorların koordinatlarını təyin etmək üçün bir sistem tərtib edirik:

Xarakterik tənliyi qururuq və həll edirik:

.
λ 1,2 = -1, λ 3 = 3.
Sistemdə λ = -1 əvəz etsək, əldə edirik:
və ya
kimi , onda iki asılı dəyişən və bir sərbəst dəyişən var.
O zaman x 1 sərbəst naməlum olsun Bu sistemi istənilən yolla həll edirik və bu sistemin ümumi həllini tapırıq: Əsas həllər sistemi bir həlldən ibarətdir, çünki n - r = 3 - 2 = 1.
λ = -1 xüsusi dəyərinə uyğun gələn xüsusi vektorlar çoxluğu formaya malikdir: , burada x 1 sıfırdan başqa istənilən ədəddir. Bu çoxluqdan bir vektor seçək, məsələn, x 1 = 1 təyin edərək: .
Oxşar şəkildə mübahisə edərək, λ = 3 xüsusi dəyərə uyğun olan xüsusi vektoru tapırıq: .
R 3 fəzasında bazis üç xətti müstəqil vektordan ibarətdir, lakin biz yalnız iki xətti müstəqil xüsusi vektor əldə etdik ki, onlardan R 3-də bazis yaratmaq mümkün deyil. Nəticə etibarilə xətti operatorun A matrisini diaqonal formaya endirmək olmaz.

Misal 13 Bir matris verilmişdir .
1. vektor olduğunu sübut edin A matrisinin xüsusi vektorudur. Bu xüsusi vektora uyğun olan xüsusi dəyəri tapın.
2. A matrisinin diaqonal formasına malik olduğu əsası tapın.
Qərar.
1. Əgər , onda xüsusi vektordur

.
Vektor (1, 8, -1) xüsusi vektordur. Xüsusi dəyər λ = -1.
Matris əsasda xüsusi vektorlardan ibarət diaqonal formaya malikdir. Onlardan biri məşhurdur. Qalanını tapaq.
Sistemdən öz vektorları axtarırıq:

Xarakterik tənlik: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
λ = -3 xüsusi dəyərinə uyğun olan xüsusi vektoru tapın:

Bu sistemin matrisinin dərəcəsi ikiyə bərabərdir və naməlumların sayına bərabərdir, ona görə də bu sistemin yalnız sıfır həlli var x 1 = x 3 = 0. Burada x 2 sıfırdan başqa hər şey ola bilər, məsələn, x 2 = 1. Beləliklə, vektor (0 ,1,0) λ = -3-ə uyğun olan xüsusi vektordur. yoxlayaq:
.
Əgər λ = 1 olarsa, sistemi alırıq
Matrisin dərəcəsi ikidir. Son tənliyi kəsin.
X 3 sərbəst naməlum olsun. Sonra x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
x 3 = 1 fərz etsək, (-3,-9,1) - λ = 1 xüsusi dəyərinə uyğun olan xüsusi vektor var. Yoxlayın:

.
Şəxsi dəyərlər həqiqi və fərqli olduğundan, onlara uyğun gələn vektorlar xətti müstəqildir, buna görə də R 3-də əsas götürülə bilər. Beləliklə, əsasda , , A matrisinin forması var:
.
A:R n → R n xətti operatorunun hər bir matrisi diaqonal formaya endirilə bilməz, çünki bəzi xətti operatorlar üçün n-dən az xətti müstəqil xüsusi vektor ola bilər. Bununla belə, əgər matris simmetrikdirsə, onda m xətti müstəqil vektorlar çoxluğun xarakterik tənliyinin kökünə uyğun gəlir.

Tərif. Simmetrik matris, əsas diaqonala görə simmetrik olan elementlərin bərabər olduğu kvadrat matrisdir, yəni .
Qeydlər. 1. Simmetrik matrisin bütün xüsusi qiymətləri həqiqidir.
2. Simmetrik matrisin cüt-cüt müxtəlif xüsusi qiymətlərə uyğun gələn xüsusi vektorları ortoqonaldır.
Tədqiq olunan aparatın çoxsaylı tətbiqlərindən biri kimi biz ikinci dərəcəli əyrinin formasının təyini problemini nəzərdən keçiririk.

Xüsusi qiymətlər (ədədlər) və xüsusi vektorlar.
Həll nümunələri

Özün ol

Hər iki tənlikdən belə nəticə çıxır.

O zaman qoyaq: .

Nəticə olaraq: ikinci xüsusi vektordur.

Gəlin vacib məqamları təkrarlayaq:

– ortaya çıxan sistemin mütləq ümumi həlli var (tənliklər xətti asılıdır);

- “Y” elə seçilib ki, tam ədəd olsun və birinci “x” koordinatı tam, müsbət və mümkün qədər kiçik olsun.

– xüsusi həllin sistemin hər bir tənliyini təmin etdiyini yoxlayırıq.

Cavab verin .

Aralıq "yoxlama məntəqələri" kifayət qədər kifayət idi, buna görə də bərabərliklərin yoxlanılması, prinsipcə, artıqdır.

Müxtəlif məlumat mənbələrində xüsusi vektorların koordinatları çox vaxt sütunlarda deyil, sətirlərdə yazılır, məsələn: (və düzünü desəm, mən özüm də onları sətirlərlə yazırdım). Bu seçim məqbuldur, lakin mövzunun işığında xətti çevrilmələr texniki cəhətdən istifadə etmək daha rahatdır sütun vektorları.

Ola bilsin ki, həll yolu sizə çox uzun göründü, amma bu, ilk nümunəni çox ətraflı şərh etdiyim üçün.

Misal 2

matrislər

Özümüz məşq edirik! Dərsin sonunda tapşırığın yekun dizaynının təxmini nümunəsi.

Bəzən əlavə tapşırıq yerinə yetirmək lazımdır, yəni:

matrisin kanonik parçalanmasını yazın

Bu nədir?

Əgər matrisin xüsusi vektorları əmələ gəlirsə əsas, onda aşağıdakı kimi təmsil oluna bilər:

Xüsusi vektorların koordinatlarından ibarət matris haradadır, – diaqonal müvafiq xüsusi qiymətləri olan matris.

Bu matrisin parçalanması adlanır kanonik və ya diaqonal.

Birinci nümunənin matrisini nəzərdən keçirin. Öz vektorları xətti müstəqil(kollinear olmayan) və əsas təşkil edir. Onların koordinatlarından matris yaradaq:

Üstündə əsas diaqonal matrislər lazımi qaydadaöz dəyərləri yerləşir və qalan elementlər sıfıra bərabərdir:
- bir daha əmrin vacibliyini vurğulayıram: "iki" 1-ci vektora uyğundur və buna görə də 1-ci sütunda, "üç" - 2-ci vektorda yerləşir.

Tapmaq üçün adi alqoritmə görə tərs matris və ya Gauss-Jordan metodu tapmaq . Xeyr, bu, hərf səhvi deyil! - sizdən əvvəl günəş tutulması kimi nadir bir hadisədir, əksi orijinal matrislə üst-üstə düşür.

Matrisin kanonik parçalanmasını yazmaq qalır:

Sistem elementar çevrilmələrdən istifadə etməklə həll edilə bilər və aşağıdakı nümunələrdə bu üsula müraciət edəcəyik. Ancaq burada "məktəb" üsulu daha sürətli işləyir. 3-cü tənlikdən ifadə edirik: - ikinci tənliyə əvəz edirik:

Birinci koordinat sıfır olduğundan, hər bir tənlikdən belə bir sistem əldə edirik.

Və yenidən xətti əlaqənin məcburi mövcudluğuna diqqət yetirin. Yalnız əhəmiyyətsiz bir həll əldə edilsə , onda ya öz dəyər səhv tapılıb, ya da sistem xəta ilə tərtib edilib/həll edilib.

Kompakt koordinatlar dəyər verir

Xüsusi vektor:

Və bir daha tapılmış həllin olduğunu yoxlayırıq sistemin hər bir tənliyini təmin edir. Sonrakı bəndlərdə və sonrakı tapşırıqlarda bu istəyin məcburi qayda kimi qəbul edilməsini tövsiyə edirəm.

2) Şəxsi dəyər üçün eyni prinsipə əməl edərək aşağıdakı sistemi əldə edirik:

Sistemin 2-ci tənliyindən ifadə edirik: - üçüncü tənliyi əvəz edirik:

"Z" koordinatı sıfıra bərabər olduğundan, hər bir tənliyindən xətti asılılıq gələn bir sistem əldə edirik.

Qoy olsun

Həll olduğunu yoxlayırıq sistemin hər bir tənliyini təmin edir.

Beləliklə, xüsusi vektor: .

3) Və nəhayət, sistem öz dəyərinə uyğundur:

İkinci tənlik ən sadə görünür, ona görə də onu ifadə edirik və onu 1-ci və 3-cü tənliklərlə əvəz edirik:

Hər şey yaxşıdır - ifadə ilə əvəz etdiyimiz xətti asılılıq aşkar edildi:

Nəticədə "X" və "Y" "Z" vasitəsilə ifadə edildi: . Praktikada yalnız belə əlaqələrə nail olmaq lazım deyil, bəzi hallarda həm vasitəsilə, həm də vasitəsilə ifadə etmək daha rahatdır. Və ya hətta "qatar" - məsələn, "X" - "Y" və "Y" - "Z"

O zaman qoyaq:

Tapılan həlli yoxlayırıq sistemin hər bir tənliyini ödəyir və üçüncü xüsusi vektoru yazın

Cavab verin: məxsus vektorlar:

Həndəsi olaraq bu vektorlar üç müxtəlif fəza istiqamətini müəyyən edir ("Orada və yenidən geri"), hansına görə xətti transformasiya sıfırdan fərqli vektorları (xüsusi vektorları) onlara kollinear vektorlara çevirir.

Əgər şərtlə -nin kanonik genişlənməsini tapmaq tələb olunurdusa, bu, burada mümkündür, çünki müxtəlif xüsusi qiymətlər müxtəlif xətti müstəqil xüsusi vektorlara uyğundur. Bir matris düzəldirik onların koordinatlarından diaqonal matris -dan müvafiq xüsusi qiymətlər və tapın tərs matris .

Şərtə görə yazmaq lazımdırsa xüsusi vektorlar əsasında xətti çevrilmə matrisi, sonra cavabı formada veririk. Bir fərq var və əhəmiyyətli bir fərq! Bu matris üçün "de" matrisidir.

Müstəqil bir həll üçün daha sadə hesablamalar olan bir tapşırıq:

Misal 5

Matrislə verilmiş xətti çevrilmənin xüsusi vektorlarını tapın

Öz nömrələrinizi taparkən, işi 3-cü dərəcəli çoxhədiyyəyə gətirməməyə çalışın. Bundan əlavə, sizin sistem həlləriniz mənim həllərimdən fərqli ola bilər - burada birmənalılıq yoxdur; və tapdığınız vektorlar nümunə vektorlarından müvafiq koordinatlarına mütənasibliyə qədər fərqli ola bilər. Məsələn, və . Cavabı şəklində təqdim etmək daha estetik baxımdan xoşdur, amma ikinci variantda dayansanız, eybi yoxdur. Ancaq hər şeyin ağlabatan məhdudiyyətləri var, versiya artıq çox yaxşı görünmür.

Dərsin sonunda tapşırığın təxmini yekun nümunəsi.

Çoxsaylı xüsusi qiymətlər olduqda problemi necə həll etmək olar?

Ümumi alqoritm eyni olaraq qalır, lakin onun özünəməxsus xüsusiyyətləri var və həllin bəzi hissələrini daha ciddi akademik üslubda saxlamaq məsləhətdir:

Misal 6

Şəxsi dəyərləri və xüsusi vektorları tapın

Qərar

Əlbəttə ki, inanılmaz birinci sütunu böyük hərflə yazaq:

Və kvadrat trinomialın faktorinqindən sonra:

Nəticədə ikisi çoxluq təşkil edən xüsusi qiymətlər əldə edilir.

Xüsusi vektorları tapaq:

1) "Sadələşdirilmiş" bir sxemə görə tək bir əsgərlə məşğul olacağıq:

Son iki tənlikdən bərabərlik aydın görünür, bu, açıq şəkildə sistemin 1-ci tənliyinə əvəz edilməlidir:

Daha yaxşı birləşmə yoxdur:
Xüsusi vektor:

2-3) İndi bir neçə gözətçini çıxarırıq. Bu vəziyyətdə ola bilər ya iki, ya bir məxsus vektor. Köklərin çoxluğundan asılı olmayaraq, determinantda dəyəri əvəz edirik , bu bizə aşağıdakıları gətirir xətti tənliklərin homojen sistemi:

Xüsusi vektorlar məhz vektorlardır
əsas qərar sistemi

Əslində, bütün dərs boyu biz ancaq fundamental sistemin vektorlarını tapmaqla məşğul olmuşuq. Hələlik bu termin xüsusi tələb olunmurdu. Yeri gəlmişkən, kamuflyajda olan çevik tələbələr homojen tənliklər, indi siqaret çəkməyə məcbur olacaq.

Yeganə tədbir əlavə xətləri silmək idi. Nəticə ortada rəsmi "addım" olan "bir-üç" matrisidir.
– əsas dəyişən, – sərbəst dəyişənlər. İki pulsuz dəyişən var, belə ki fundamental sistemin iki vektoru da var.

Baza dəyişənini sərbəst dəyişənlərlə ifadə edək: . "X" qarşısındakı sıfır faktoru ona tamamilə hər hansı bir dəyəri almağa imkan verir (bu, tənliklər sistemindən də aydın görünür).

Bu problemin kontekstində ümumi həlli sətirdə deyil, sütunda yazmaq daha rahatdır:

Cütlük xüsusi vektora uyğundur:
Cütlük xüsusi vektora uyğundur:

Qeyd : mükəmməl oxucular bu vektorları şifahi olaraq götürə bilərlər - sadəcə sistemi təhlil etməklə , lakin burada bəzi biliklərə ehtiyac var: üç dəyişən var, sistem matrisinin dərəcəsi- vahid deməkdir əsas qərar sistemi 3 – 1 = 2 vektordan ibarətdir. Bununla belə, aşkar edilmiş vektorlar hətta bu məlumat olmadan, sırf intuitiv səviyyədə mükəmməl görünür. Bu halda üçüncü vektor daha da “daha ​​gözəl” yazılacaq: . Bununla belə, sizə xəbərdarlıq edirəm, başqa bir misalda, sadə seçim olmaya bilər, buna görə rezervasiya təcrübəli insanlar üçün nəzərdə tutulub. Bundan əlavə, niyə üçüncü vektor kimi qəbul etməyək, deyək ki, ? Axı onun koordinatları da sistemin hər bir tənliyini və vektorlarını ödəyir xətti müstəqildirlər. Bu seçim, prinsipcə, uyğundur, lakin "əyri", çünki "digər" vektor əsas sistemin vektorlarının xətti birləşməsidir.

Cavab verin: xüsusi qiymətlər: , xüsusi vektorlar:

Öz əlinizlə həll üçün oxşar bir nümunə:

Misal 7

Şəxsi dəyərləri və xüsusi vektorları tapın

Dərsin sonunda bitirmənin təxmini nümunəsi.

Qeyd etmək lazımdır ki, həm 6-cı, həm də 7-ci nümunələrdə üçlü xətti müstəqil xüsusi vektorlar alınır və buna görə də orijinal matris kanonik genişlənmədə təmsil oluna bilər. Ancaq belə moruq bütün hallarda olmur:

Misal 8

Qərar: xarakterik tənliyi qurun və həll edin:

Determinantı birinci sütunla genişləndiririk:

3-cü dərəcəli polinomdan qaçaraq, nəzərdən keçirilən üsula uyğun olaraq əlavə sadələşdirmələr aparırıq:

xüsusi qiymətlərdir.

Xüsusi vektorları tapaq:

1) Köklə bağlı heç bir çətinlik yoxdur:

Təəccüblənməyin, dəstdən əlavə, dəyişənlər də istifadə olunur - burada heç bir fərq yoxdur.

3-cü tənlikdən ifadə edirik - 1-ci və 2-ci tənlikləri əvəz edirik:

Hər iki tənlikdən belə çıxır:

Qoy o zaman:

2-3) Çoxsaylı dəyərlər üçün sistemi alırıq .

Sistemin matrisini yazaq və elementar çevrilmələrdən istifadə edərək onu pilləli formaya gətirək:

www.site tapmağa imkan verir. Sayt hesablama aparır. Bir neçə saniyədən sonra server düzgün həlli verəcəkdir. Matris üçün xarakterik tənlik determinantın hesablanması qaydası ilə tapılan cəbri ifadə olacaq matrislər matrislər, əsas diaqonalda isə diaqonal elementlərin və dəyişənin dəyərlərində fərqlər olacaq. Hesablayarkən matris üçün xarakterik tənlik online, hər bir element matrislər müvafiq digər elementlərlə vurulacaq matrislər. Rejimdə tapın onlayn yalnız kvadrat üçün mümkündür matrislər. Əməliyyatı tapın matris üçün xarakterik tənlik online elementlərin hasilinin cəbri cəminin hesablanmasına qədər azaldır matrislər təyinedicinin tapılması nəticəsində matrislər, yalnız müəyyən etmək məqsədi ilə matris üçün xarakterik tənlik online. Bu əməliyyat nəzəriyyədə xüsusi yer tutur matrislər, köklərdən istifadə edərək öz dəyərləri və vektorları tapmağa imkan verir. Tapşırıq tapşırığı matris üçün xarakterik tənlik online elementləri çoxaltmaqdır matrislər müəyyən bir qaydaya uyğun olaraq bu məhsulların sonrakı cəmlənməsi ilə. www.site tapır matris üçün xarakterik tənlik rejimdə verilmiş ölçü onlayn. hesablama matris üçün xarakterik tənlik online verilmiş ölçü üçün bu, determinantın hesablanması qaydası ilə tapılan ədədi və ya simvolik əmsalları olan çoxhədli tapmaqdır. matrislər- müvafiq elementlərin məhsullarının cəmi kimi matrislər, yalnız müəyyən etmək məqsədi ilə matris üçün xarakterik tənlik online. Kvadrat üçün dəyişənə görə çoxhədlinin tapılması matrislər, tərif kimi matris üçün xarakterik tənlik, nəzəri cəhətdən ümumi matrislər. Çoxhədlinin köklərinin qiyməti matris üçün xarakterik tənlik onlineüçün xüsusi vektorları və xüsusi dəyərləri müəyyən etmək üçün istifadə olunur matrislər. Ancaq determinant olarsa matrislər onda sıfır olacaq matris xarakteristikası tənliyiəksindən fərqli olaraq hələ də mövcud olacaq matrislər. Hesablamaq üçün matris üçün xarakterik tənlik və ya eyni anda bir neçə axtarın matrislərin xarakterik tənlikləri, çox vaxt və səy sərf etməli, serverimiz tapacaq onlayn matris üçün xarakterik tənlik. Bu vəziyyətdə cavab tapmaqla matris üçün xarakterik tənlik onlineədədləri taparkən belə düzgün və kifayət qədər dəqiqliklə olacaq matris üçün xarakterik tənlik online irrasional olacaq. Onlayn www.site elementlərdə simvol girişlərinə icazə verilir matrislər, yəni onlayn matris üçün xarakterik tənlik hesablanarkən ümumi simvolik formada təmsil oluna bilər xarakterik tənlik matrisi online. Tapma məsələsini həll edərkən alınan cavabı yoxlamaq faydalıdır matris üçün xarakterik tənlik online saytdan istifadə etməklə www.site. Polinomun hesablanması əməliyyatını yerinə yetirərkən - matrisin xarakterik tənliyi, bu problemin həllində diqqətli və son dərəcə diqqətli olmaq lazımdır. Öz növbəsində saytımız mövzu ilə bağlı qərarınızı yoxlamaqda sizə kömək edəcək xarakterik tənlik matrisi online. Əgər həll olunan problemlərin uzun müddət yoxlanılmasına vaxtınız yoxdursa, o zaman www.site tapmaq və hesablamaq üçün əlbəttə ki, yoxlamaq üçün əlverişli bir vasitədir matris üçün xarakterik tənlik online.

Kvadrat matrisin öz vektoru odur ki, verilmiş matrislə vurulduqda kollinear vektor yaranır. Sadə sözlə desək, bir matris öz vektoru ilə vurulduqda, sonuncu eyni qalır, lakin bəzi ədədə vurulur.

Tərif

Öz vektor sıfırdan fərqli V vektordur, M kvadrat matrisə vurulduqda özünə çevrilir, müəyyən λ ədədi ilə artır. Cəbri notasiyada bu belə görünür:

M × V = λ × V,

burada λ M matrisinin xüsusi dəyəridir.

Rəqəmsal bir misala baxaq. Yazının rahatlığı üçün matrisdəki nömrələr nöqtəli vergüllə ayrılacaq. Tutaq ki, bizim bir matrisimiz var:

• M = 0; 4;
• 6; 10.

Onu sütun vektoruna vuraq:

• V = -2;

Bir matrisi sütun vektoruna vurduqda, biz də sütun vektoru alırıq. Ciddi riyazi dildə, 2 × 2 matrisi sütun vektoruna vurmaq üçün düstur belə görünür:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 birinci cərgədə və birinci sütunda duran M matrisinin elementini, M22 isə ikinci sətirdə və ikinci sütunda yerləşən elementi bildirir. Matrisimiz üçün bu elementlər M11 = 0, M12 = 4, M21 = 6, M22 10-dur. Sütun vektoru üçün bu dəyərlər V11 = –2, V21 = 1-dir. Bu düstura görə aşağıdakıları alırıq. kvadrat matrisin vektorla hasilinin nəticəsi:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Rahatlıq üçün sütun vektorunu bir sıraya yazırıq. Beləliklə, kvadrat matrisi vektora (-2; 1) vurduq, nəticədə (4; -2) vektoru əldə etdik. Aydındır ki, bu λ = -2 ilə vurulan eyni vektordur. Lambda bu halda matrisin öz dəyərini bildirir.

Bir matrisin xüsusi vektoru kollinear vektordur, yəni bir matrislə vurulduqda fəzada mövqeyini dəyişməyən bir cisimdir. Vektor cəbrində kollinearlıq anlayışı həndəsədəki paralellik termininə bənzəyir. Həndəsi şərhdə kollinear vektorlar müxtəlif uzunluqlu paralel istiqamətlənmiş seqmentlərdir. Evklid dövründən bəri biz bilirik ki, tək bir xəttin ona paralel sonsuz sayda xətləri var, ona görə də hər bir matrisin sonsuz sayda öz vektoru olduğunu düşünmək məntiqlidir.

Əvvəlki nümunədən görmək olar ki, həm (-8; 4), həm də (16; -8) və (32, -16) öz vektor ola bilər. Bütün bunlar λ = -2 xüsusi dəyərə uyğun gələn kollinear vektorlardır. Orijinal matrisi bu vektorlara vurduqda biz yenə də nəticədə orijinaldan 2 dəfə fərqlənən vektor alacağıq. Məhz buna görə də məxsi vektoru tapmaq üçün məsələləri həll edərkən yalnız xətti müstəqil vektor obyektlərini tapmaq tələb olunur. Çox vaxt n × n matrisi üçün n-ci sayda xüsusi vektorlar olur. Kalkulyatorumuz ikinci dərəcəli kvadrat matrislərin təhlili üçün nəzərdə tutulmuşdur, ona görə də, üst-üstə düşdüyü hallar istisna olmaqla, nəticədə demək olar ki, həmişə iki məxsusi vektor tapılacaqdır.

Yuxarıdakı misalda biz əvvəlcədən orijinal matrisin öz vektorunu bilirdik və lambda sayını vizual olaraq təyin etdik. Bununla belə, praktikada hər şey tərsinə baş verir: başlanğıcda xüsusi qiymətlər və yalnız bundan sonra xüsusi vektorlar var.

Həll alqoritmi

Orijinal M matrisinə yenidən baxaq və onun hər iki məxsus vektorunu tapmağa çalışaq. Beləliklə, matris belə görünür:

• M = 0; 4;
• 6; 10.

Başlamaq üçün, λ xüsusi dəyərini təyin etməliyik, bunun üçün aşağıdakı matrisin determinantını hesablamalıyıq:

• (0 − λ); 4;
• 6; (10 − λ).

Bu matris əsas diaqonaldakı elementlərdən naməlum λ çıxılmaqla əldə edilir. Determinant standart düsturla müəyyən edilir:

• detA = M11 × M21 - M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Vektorumuz sıfır olmamalıdır, nəticədə yaranan tənliyi xətti asılı olaraq qəbul edirik və determinantımızı detA-nı sıfıra bərabərləşdiririk.

(0 − λ) × (10 − λ) − 24 = 0

Mötərizələri açaq və matrisin xarakterik tənliyini əldə edək:

λ 2 − 10λ − 24 = 0

Bu, diskriminant baxımından həll edilməli olan standart kvadrat tənlikdir.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Diskriminantın kökü sqrt(D) = 14-dür, ona görə də λ1 = -2, λ2 = 12. İndi hər bir lambda dəyəri üçün biz xüsusi vektor tapmalıyıq. λ = -2 üçün sistemin əmsallarını ifadə edək.

• M − λ × E = 2; 4;
• 6; 12.

Bu düsturda E eynilik matrisidir. Alınan matrisə əsasən xətti tənliklər sistemini tərtib edirik:

2x + 4y = 6x + 12y

burada x və y xüsusi vektorun elementləridir.

Soldakı bütün X-ləri və sağdakı bütün Y-ləri toplayaq. Aydındır ki, - 4x = 8y. İfadəni - 4-ə bölün və x = -2y alın. İndi naməlumların istənilən qiymətini götürərək matrisin birinci xüsusi vektorunu təyin edə bilərik (xətti asılı olan xüsusi vektorların sonsuzluğunu xatırlayın). y = 1 götürək, onda x = -2. Buna görə də birinci xüsusi vektor V1 = (–2; 1) kimi görünür. Məqalənin əvvəlinə qayıdın. Məhz bu vektor obyekti idi ki, biz xüsusi vektor anlayışını nümayiş etdirmək üçün matrisi çoxaldıq.

İndi λ = 12 üçün məxsusi vektoru tapaq.

• M - λ × E = -12; 4
• 6; -2.

Eyni xətti tənliklər sistemini tərtib edək;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x=y.

İndi x = 1 götürək, deməli, y = 3. Beləliklə, ikinci xüsusi vektor V2 = (1; 3) kimi görünür. Orijinal matrisi bu vektora vurduqda, nəticə həmişə eyni vektorun 12-yə vurulması olacaq. Bu, həll alqoritmini tamamlayır. İndi siz matrisin öz vektorunu əl ilə necə təyin edəcəyinizi bilirsiniz.

• təyinedici;
• iz, yəni əsas diaqonaldakı elementlərin cəmi;
• dərəcə, yəni xətti müstəqil sətirlərin/sütunların maksimum sayı.

Proqram həll prosesini minimuma endirərək yuxarıda göstərilən alqoritmə uyğun işləyir. Qeyd etmək lazımdır ki, proqramda lambda "c" hərfi ilə işarələnir. Rəqəmsal bir nümunəyə baxaq.

Proqram nümunəsi

Aşağıdakı matris üçün xüsusi vektorları təyin etməyə çalışaq:

• M=5; on üç;
• 4; 14.

Gəlin bu dəyərləri kalkulyatorun xanalarına daxil edək və cavabı aşağıdakı formada alaq:

• Matris dərəcəsi: 2;
• Matris təyinedicisi: 18;
• Matris izi: 19;
• Özvektorun hesablanması: c 2 − 19.00c + 18.00 (xarakteristik tənlik);
• Özvektorun hesablanması: 18 (birinci lambda dəyəri);
• Özvektorun hesablanması: 1 (ikinci lambda dəyəri);
• 1-ci vektorun tənliklər sistemi: -13x1 + 13y1 = 4x1 − 4y1;
• Vektor 2 tənlik sistemi: 4x1 + 13y1 = 4x1 + 13y1;
• Xüsusi vektor 1: (1; 1);
• Xüsusi vektor 2: (-3,25; 1).

Beləliklə, iki xətti müstəqil xüsusi vektor əldə etdik.

Nəticə

Xətti cəbr və analitik həndəsə mühəndislik üzrə istənilən birinci kurs tələbəsi üçün standart fənlərdir. Çoxlu sayda vektor və matrislər dəhşətlidir və belə çətin hesablamalarda səhv etmək asandır. Proqramımız tələbələrə öz hesablamalarını yoxlamağa və ya öz vektoru tapmaq məsələsini avtomatik həll etməyə imkan verəcək. Kataloqumuzda başqa xətti cəbr kalkulyatorları var, onlardan dərsinizdə və ya işinizdə istifadə edin.

". Birinci hissədə kimyometrikanı başa düşmək üçün minimal zəruri olan müddəalar, ikinci hissədə çoxvariantlı analiz üsullarını daha dərindən başa düşmək üçün bilməli olduğunuz faktlar var. Təqdimat Excel iş kitabında hazırlanmış nümunələrlə təsvir edilmişdir. Matrix.xls bu sənədi müşayiət edir.

Nümunələrə keçidlər mətndə Excel obyektləri kimi yerləşdirilir. Bu misallar mücərrəd xarakter daşıyır, heç bir halda analitik kimya problemlərinə bağlı deyillər. Kimometriyada matris cəbrinin istifadəsinin real nümunələri müxtəlif kimyometrik tətbiqlərə həsr olunmuş digər mətnlərdə müzakirə olunur.

Analitik kimyada aparılan ölçmələrin əksəriyyəti birbaşa deyil, lakin dolayı. Bu o deməkdir ki, təcrübədə istənilən analitin C qiymətinin (konsentrasiya) əvəzinə başqa qiymət alınır. x(siqnal) C ilə əlaqəli, lakin ona bərabər deyil, yəni. x(C) ≠ C. Bir qayda olaraq, asılılığın növü x(C) məlum deyil, amma xoşbəxtlikdən analitik kimyada ölçmələrin çoxu mütənasibdir. Bu o deməkdir ki, C konsentrasiyası olaraq a dəfə, X siqnalı eyni miqdarda artacaq., yəni. x(a C) = a x(C). Bundan əlavə, siqnallar da əlavədir, belə ki, C 1 və C 2 konsentrasiyası olan iki maddədən ibarət nümunədən gələn siqnal hər bir komponentdən gələn siqnalların cəminə bərabər olacaqdır, yəni. x(C1 + C2) = x(C1)+ x(C2). Mütənasiblik və əlavəlik birlikdə verir xəttilik. Xəttilik prinsipini göstərmək üçün çoxlu misallar vermək olar, lakin bunun üçün ən parlaq iki nümunəni - xromatoqrafiya və spektroskopiyanı qeyd etmək kifayətdir. Analitik kimyada təcrübəyə xas olan ikinci xüsusiyyət çoxkanallı. Müasir analitik avadanlıq eyni vaxtda bir çox kanal üçün siqnalları ölçür. Məsələn, işığın ötürülməsinin intensivliyi bir anda bir neçə dalğa uzunluğu üçün ölçülür, yəni. diapazon. Buna görə də, təcrübədə biz müxtəlif siqnallarla məşğul oluruq x 1 , x 2 ,...., x n tədqiq olunan sistemdə mövcud olan maddələrin C 1 ,C 2 , ..., C m konsentrasiyaları toplusunu xarakterizə edən n.

düyü. 1 Spektr

Beləliklə, analitik təcrübə xətti və çoxölçülü olması ilə xarakterizə olunur. Buna görə də eksperimental məlumatları vektor və matris kimi nəzərdən keçirmək və onları matris cəbri aparatından istifadə etməklə manipulyasiya etmək rahatdır. Bu yanaşmanın məhsuldarlığı 4000-dən 4796 sm-1-ə qədər 200 dalğa uzunluğu üçün götürülmüş üç spektri göstərən misalda göstərilir. ilk ( x 1) və ikinci ( x 2) iki A və B maddəsinin konsentrasiyası məlum olan standart nümunələr üçün spektrlər alınmışdır: birinci nümunədə [A] = 0,5, [B] = 0,1, ikinci nümunədə [A] = 0,2, [ B] = 0,6. Spektri göstərilən yeni, naməlum nümunə haqqında nə demək olar x 3 ?

Üç eksperimental spektri nəzərdən keçirin x 1 , x 2 və x 3-ü 200 ölçüsünün üç vektoru kimi. Xətti cəbrdən istifadə etməklə bunu asanlıqla göstərmək olar x 3 = 0.1 x 1 +0.3 x 2, buna görə də üçüncü nümunədə açıq-aydın yalnız konsentrasiyalarda A və B maddələri var [A] = 0,5×0,1 + 0,2×0,3 = 0,11 və [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Əsas məlumat

1.1 Matrislər

Matris məsələn, düzbucaqlı rəqəmlər cədvəli adlanır

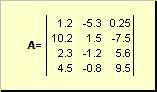
düyü. 2 Matris

Matrislər böyük qalın hərflərlə işarələnir ( A), və onların elementləri - indeksləri olan müvafiq kiçik hərflərlə, yəni. a ij . Birinci indeks sətirləri, ikincisi isə sütunları nömrələyir. Kimyometrikada indeksin maksimum dəyərini indeksin özü ilə eyni hərflə, lakin böyük hərflərlə təyin etmək adətdir. Beləliklə, matris A kimi də yazıla bilər ( a ij , i = 1,..., I; j = 1,..., J). Məsələn matris üçün I = 4, J= 3 və a 23 = −7.5.

Cüt nömrələr I və J matrisin ölçüsü adlanır və kimi işarələnir I× J. Kimometriyada matrisin nümunəsi üçün alınan spektrlər toplusudur I nümunələri üzərində J dalğa uzunluqları.

1.2. Matrislərlə ən sadə əməliyyatlar

Matrislər bilər ədədlərlə çarpın. Bu halda, hər bir element bu rəqəmə vurulur. Misal üçün -

düyü. 3 Matrisin ədədə vurulması

Eyni ölçülü iki matris element baxımından ola bilər qat və çıxmaq. Misal üçün,

düyü. 4 Matris əlavəsi

Ədədlə vurma və toplama nəticəsində eyni ölçülü matris alınır.

Sıfır matris sıfırlardan ibarət matrisdir. Təyin olunub O. Aydındır ki A+O = A, A−A = O və 0 A = O.

Matris bilər köçürmək. Bu əməliyyat zamanı matris çevrilir, yəni. sətirlər və sütunlar dəyişdirilir. Transpozisiya tire ilə göstərilir, A" və ya indeks A t . Beləliklə, əgər A = {a ij , i = 1,..., I; j = 1,...,J), sonra A t = ( a ji , j = 1,...,J; i = 1,..., I). misal üçün

düyü. 5 Matrisin köçürülməsi

Aydındır ki ( A t) t = A, (A+B) t = A t + B t .

1.3. Matrisin vurulması

Matrislər bilər çoxalmaq, lakin yalnız müvafiq ölçülərə malik olduqda. Bunun niyə belə olduğu tərifdən aydın olacaq. Matris məhsulu A, ölçü I× K, və matrislər B, ölçü K× J, matris adlanır C, ölçü I× J, elementləri ədədlərdir

Beləliklə, məhsul üçün AB sol matrisdəki sütunların sayının olması lazımdır A sağ matrisdəki cərgələrin sayına bərabər idi B. Matris məhsul nümunəsi -

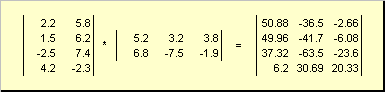
Şəkil.6 Matrislərin hasili

Matris vurma qaydası aşağıdakı kimi tərtib edilə bilər. Matrisin elementini tapmaq üçün C kəsişməsində dayanır i-ci xətt və j-ci sütun ( c ij) elementi elementə vurmaq lazımdır i-birinci matrisin cərgəsi Aüstündə j ikinci matrisin -ci sütunu B və bütün nəticələri əlavə edin. Beləliklə, göstərilən nümunədə üçüncü cərgənin və ikinci sütunun elementi üçüncü sıranın element baxımından məhsullarının cəmi kimi alınır. A və ikinci sütun B

Şəkil.7 Matrislərin hasilinin elementi

Matrislərin məhsulu sıradan asılıdır, yəni. AB ≠ BA, ən azı ölçülü səbəblərə görə. Onun qeyri-kommutativ olduğu deyilir. Bununla belə, matrislərin hasili assosiativdir. Bu o deməkdir ki ABC = (AB)C = A(e.ə). Üstəlik, o, həm də paylayıcıdır, yəni. A(B+C) = AB+AC. Aydındır ki AO = O.

1.4. Kvadrat matrislər

Əgər matrisin sütunlarının sayı onun sətirlərinin sayına bərabərdirsə ( I = J=N), onda belə bir matris kvadrat adlanır. Bu bölmədə yalnız belə matrisləri nəzərdən keçirəcəyik. Bu matrislər arasında xüsusi xassələrə malik matrisləri ayırmaq olar.

Tək matris (ifadə olunur I və bəzən E) 1-ə bərabər olan diaqonallar istisna olmaqla, bütün elementlərinin sıfıra bərabər olduğu bir matrisdir, yəni.

Aydındır ki AI = İA = A.

Matris deyilir diaqonal, əgər onun bütün elementləri, diaqonallardan başqa ( a ii) sıfıra bərabərdir. misal üçün

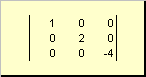
düyü. 8 Diaqonal matris

Matris Aüst adlanır üçbucaqlı, əgər onun diaqonaldan aşağıda yerləşən bütün elementləri sıfıra bərabərdirsə, yəni. a ij= 0, at i>j. misal üçün

düyü. 9 Üst üçbucaqlı matris

Aşağı üçbucaqlı matris eyni şəkildə müəyyən edilir.

Matris Açağırdı simmetrik, əgər A t = A. Başqa sözlə a ij = a ji. misal üçün

düyü. 10 Simmetrik matris

Matris Açağırdı ortoqonal, əgər

A t A = AA t = I.

Matris deyilir normaləgər

1.5. İz və determinant

İzləyir kvadrat matris A(Tr( A) və ya Sp( A)) onun diaqonal elementlərinin cəmidir,

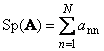
Misal üçün,

düyü. 11 Matris izi

Aydındır ki

Sp(α A) = α Sp( A) və

Sp( A+B) = Sp( A)+ Sp( B).

Bunu göstərmək olar

Sp( A) = Sp( A t), Sp( I) = N,

həm də ki

Sp( AB) = Sp( BA).

Kvadrat matrisin digər vacib xüsusiyyəti onun olmasıdır təyinedici(det( ilə işarələnir) A)). Ümumi vəziyyətdə müəyyənedicinin tərifi olduqca mürəkkəbdir, ona görə də ən sadə variantdan - matrisdən başlayacağıq. Aölçüsü (2×2). Sonra

(3×3) matris üçün determinant bərabər olacaq

Matris halda ( N× N) determinant 1 2 3 ... cəmi kimi hesablanır. N= N! hər biri bərabər olan şərtlər

İndekslər k 1 , k 2 ,..., k N bütün mümkün sifarişli dəyişdirmələr kimi müəyyən edilir r dəstdəki nömrələr (1, 2, ... , N). Matris determinantının hesablanması praktikada xüsusi proqramlardan istifadə etməklə həyata keçirilən mürəkkəb prosedurdur. Misal üçün,

düyü. 12 Matris təyinedicisi

Yalnız aşkar xüsusiyyətləri qeyd edirik:

det( I) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. Vektorlar

Əgər matrisin yalnız bir sütunu varsa ( J= 1), onda belə bir obyekt çağırılır vektor. Daha doğrusu, sütun vektoru. misal üçün

Məsələn, bir sıradan ibarət matrislər də nəzərdən keçirilə bilər

Bu obyekt də vektordur, lakin sıra vektoru. Məlumatları təhlil edərkən hansı vektorlarla - sütunlar və ya sətirlərlə məşğul olduğumuzu anlamaq vacibdir. Beləliklə, bir nümunə üçün götürülmüş spektri bir sıra vektoru hesab etmək olar. Sonra bütün nümunələr üçün müəyyən dalğa uzunluğunda spektral intensivliklər dəsti sütun vektoru kimi qəbul edilməlidir.

Vektorun ölçüsü onun elementlərinin sayıdır.

Aydındır ki, istənilən sütun vektoru transpozisiya ilə sətir vektoruna çevrilə bilər, yəni.

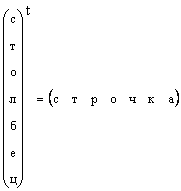
Vektorun formasının xüsusi olaraq göstərilmədiyi, sadəcə vektor deyildiyi hallarda, onlar sütun vektoru deməkdir. Biz də bu qaydaya əməl edəcəyik. Vektor kiçik hərflə birbaşa qalın hərflə işarələnir. Sıfır vektoru bütün elementləri sıfıra bərabər olan vektordur. İşarə olunur 0 .

1.7. Vektorlarla ən sadə əməliyyatlar

Vektorlar matrislərlə eyni şəkildə ədədlərə əlavə edilə və vurula bilər. Misal üçün,

düyü. 13 Vektorlarla əməliyyatlar

İki vektor x və yçağırdı kollinear, əgər belə bir α ədədi varsa

1.8. Vektorların məhsulları

Eyni ölçülü iki vektor Nçoxalda bilər. İki vektor olsun x = (x 1 , x 2 ,...,x N) t və y = (y 1 , y 2 ,...,y N) t . "Sətrə sütun" vurma qaydasını rəhbər tutaraq onlardan iki məhsul yarada bilərik: x t y və xy t . İlk iş

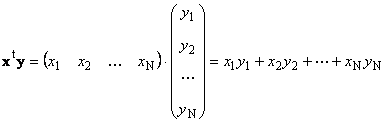
çağırdı skalyar və ya daxili. Onun nəticəsi rəqəmdir. O, həmçinin qeyddən istifadə edir ( x,y)= x t y. Misal üçün,

düyü. 14 Daxili (skalyar) hasil

İkinci iş

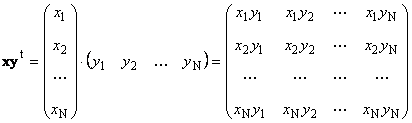
çağırdı xarici. Onun nəticəsi ölçü matrisidir ( N× N). Misal üçün,

düyü. 15 Xarici məhsul

Skayar hasilinin sıfıra bərabər olduğu vektorlar deyilir ortoqonal.

1.9. Vektor norması

Vektorun özü ilə skalyar hasilinə skalyar kvadrat deyilir. Bu dəyər

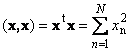
kvadrat müəyyən edir uzunluq vektor x. Uzunluğu ifadə etmək üçün (həmçinin deyilir norma vektor) qeydindən istifadə olunur

Misal üçün,

düyü. 16 Vektor norması

Vahid uzunluq vektoru (|| x|| = 1) normallaşdırılmış adlanır. Sıfırdan fərqli vektor ( x ≠ 0 ) uzunluğa bölmək yolu ilə normallaşdırıla bilər, yəni. x = ||x|| (x/||x||) = ||x|| e. Budur e = x/||x|| normallaşdırılmış vektordur.

Vektorların hamısı normallaşdırılmış və cüt-cüt ortoqonal olarsa ortonormal adlanır.

1.10. Vektorlar arasındakı bucaq

Skayar hasil və müəyyən edir inyeksiya iki vektor arasında φ x və y

Əgər vektorlar ortoqonaldırsa, o zaman cosφ = 0 və φ = π/2, kollineardırsa, o zaman cosφ = 1 və φ = 0 olur.

1.11. Matrisin vektor təsviri

Hər bir matris Aölçüsü I× J vektorlar toplusu kimi təmsil oluna bilər

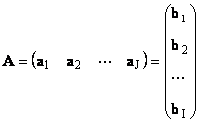
Burada hər bir vektor a j birdir j-ci sütun və sətir vektoru b i birdir i matrisin -ci sıra A

1.12. Xətti asılı vektorlar

Eyni ölçülü vektorlar ( N) ədədi matrislər kimi ədədlə toplamaq və vurmaq olar. Nəticə eyni ölçülü vektordur. Eyni ölçülü bir neçə vektor olsun x 1 , x 2 ,...,x K və eyni sayda α α 1 , α 2 ,...,α K. Vektor

y= α 1 x 1 + α 2 x 2 +...+α K x K

çağırdı xətti birləşmə vektorlar x k .

Əgər belə sıfırdan fərqli ədədlər varsa α k ≠ 0, k = 1,..., K, nə y = 0 , onda belə vektorlar toplusu x kçağırdı xətti asılı. Əks halda vektorlar xətti müstəqil adlanır. Məsələn, vektorlar x 1 = (2, 2) t və x 2 = (−1, −1) t xətti asılıdır, çünki x 1 +2x 2 = 0

1.13. Matris dərəcəsi

bir sıra düşünün K vektorlar x 1 , x 2 ,...,x Kölçüləri N. Bu vektorlar sisteminin dərəcəsi xətti müstəqil vektorların maksimum sayıdır. Məsələn, dəstdə

məsələn, yalnız iki xətti müstəqil vektor var x 1 və x 2, buna görə də onun dərəcəsi 2-dir.

Aydındır ki, əgər dəstdə onların ölçüsündən daha çox vektor varsa ( K>N), onda onlar mütləq xətti asılı olurlar.

Matris dərəcəsi(rütbə ilə işarələnir( A)) ibarət olduğu vektorlar sisteminin dərəcəsidir. Hər hansı bir matris iki şəkildə (sütun vektorları və ya cərgə vektorları) təmsil oluna bilsə də, bu, dərəcə dəyərinə təsir göstərmir, çünki

1.14. tərs matris

kvadrat matris Aözünəməxsus xüsusiyyətə malikdirsə qeyri-degenerativ adlanır tərs matris A-1 , şərtlərlə müəyyən edilir

AA −1 = A −1 A = I.

Əks matris bütün matrislər üçün mövcud deyil. Qeyri-degenerativlik üçün zəruri və kafi şərtdir

det( A) ≠ 0 və ya dərəcə( A) = N.

Matrisin çevrilməsi xüsusi proqramların mövcud olduğu mürəkkəb bir prosedurdur. Misal üçün,

düyü. 17 Matrisin inversiyası

Ən sadə hal üçün düsturlar veririk - matrislər 2 × 2

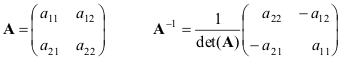
Əgər matrislər A və B degenerasiyaya uğramırlar

(AB) −1 = B −1 A −1 .

1.15. Pseudo-ters matris

Əgər matris A degenerativdir və tərs matris mövcud deyilsə, bəzi hallarda istifadə edilə bilər yalançı tərs belə bir matris kimi müəyyən edilən matris A+ o

AA + A = A.

Yalançı tərs matris tək deyil və onun forması tikinti üsulundan asılıdır. Məsələn, düzbucaqlı matris üçün Mur-Penrose metodundan istifadə edə bilərsiniz.

Əgər sütunların sayı sətirlərin sayından azdırsa, o zaman

A + =(A t A) −1 A t

Misal üçün,

düyü. 17a Pseudo matris inversion

Sütunların sayı sətirlərin sayından çox olarsa, o zaman

A + =A t ( AA t) −1

1.16. Bir vektorun matrisə vurulması

Vektor x matrislə vurula bilər A uyğun ölçü. Bu halda sütun vektoru sağda vurulur balta, və vektor sətri soldadır x t A. Əgər vektorun ölçüsü J, və matrisin ölçüsü I× J onda nəticə ölçü vektorudur I. Misal üçün,

düyü. 18 Vektor-Matrisin vurulması

Əgər matris A- kvadrat ( I× I), sonra vektor y = balta ilə eyni ölçüyə malikdir x. Aydındır ki

A(α 1 x 1 + α 2 x 2) = α 1 balta 1 + α 2 balta 2 .

Buna görə də matrisləri vektorların xətti çevrilmələri hesab etmək olar. Xüsusilə x = x, öküz = 0 .

2. Əlavə məlumat

2.1. Xətti tənliklər sistemləri

Qoy olsun A- matrisin ölçüsü I× J, a b- ölçü vektoru J. Tənliyi nəzərdən keçirin

balta = b

vektora münasibətdə x, ölçüləri I. Əslində, bu bir sistemdir I ilə xətti tənliklər J naməlum x 1 ,...,x J. Həll yalnız və yalnız o halda mövcuddur

dərəcə ( A) = dərəcə( B) = R,

harada B artırılmış ölçü matrisidir I×( J+1) matrisdən ibarətdir A, bir sütunla doldurulmuşdur b, B = (A b). Əks halda, tənliklər uyğunsuzdur.

Əgər a R = I = J, onda həll unikaldır

x = A −1 b.

Əgər a R < I, onda xətti birləşmə ilə ifadə edilə bilən çoxlu müxtəlif həllər var J−R vektorlar. Homojen tənliklər sistemi balta = 0 kvadrat matris ilə A (N× N) qeyri-trivial həlli var ( x ≠ 0 ) əgər və ancaq det( A) = 0. Əgər R= dərəcə( A)<N, onda var N−R xətti müstəqil həllər.

2.2. İkixətti və kvadrat formalar

Əgər a A kvadrat matrisdir və x və y- müvafiq ölçünün vektorları, sonra formanın skalyar hasili x t Ayçağırdı ikixətli matris tərəfindən müəyyən edilmiş forma A. At x = y ifadə x t baltaçağırdı kvadratik forma.

2.3. Müsbət müəyyən matrislər

kvadrat matris Açağırdı müsbət müəyyən, hər hansı sıfırdan fərqli vektor üçün x ≠ 0 ,

x t balta > 0.

The mənfi (x t balta < 0), mənfi olmayan (x t balta≥ 0) və qeyri-müsbət (x t balta≤ 0) müəyyən matrislər.

2.4. Xoleskinin parçalanması

Əgər simmetrik matris A müsbət müəyyəndir, onda unikal üçbucaqlı matris var U müsbət elementlərlə, bunun üçün

A = U t U.

Misal üçün,

düyü. 19 Xoleskinin parçalanması

2.5. qütb parçalanması

Qoy olsun Aölçünün degenerasiya olunmayan kvadrat matrisidir N× N. Sonra unikal var qütb performans

A = SR,

harada S qeyri-mənfi simmetrik matrisdir və R ortoqonal matrisdir. matrislər S və R aydın şəkildə müəyyən edilə bilər:

S 2 = AA t və ya S = (AA t) ½ və R = S −1 A = (AA t) −½ A.

Misal üçün,

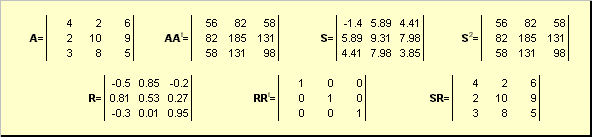
düyü. 20 Qütb parçalanması

Əgər matris A degenerativdir, onda parçalanma unikal deyil - yəni: S hələ də tək, amma Rçox ola bilər. Qütb parçalanma matrisi təmsil edir A sıxılma/uzatma birləşməsi kimi S və fırlanma R.

2.6. Xüsusi vektorlar və xüsusi qiymətlər

Qoy olsun A kvadrat matrisdir. Vektor vçağırdı öz vektoru matrislər A, əgər

Av = λ v,

λ nömrəsinin çağırıldığı yer xüsusi dəyər matrislər A. Beləliklə, matrisin həyata keçirdiyi çevrilmə A vektor üzərində v, λ faktoru ilə sadə bir uzanma və ya sıxılmaya endirilir. Xüsusi vektor α ≠ 0 sabiti ilə vurulana qədər müəyyən edilir, yəni. əgər v xüsusi vektordur, onda α v həm də xüsusi vektordur.

2.7. Xüsusi dəyərlər

Matrisdə A, ölçü ( N× N) -dən böyük ola bilməz Nözəl dəyərlər. Onlar qane edir xarakterik tənlik

det( A − λ I) = 0,

cəbri tənlikdir N-ci sifariş. Xüsusilə, 2×2 matris üçün xarakterik tənlik formaya malikdir

Misal üçün,

düyü. 21 Xüsusi qiymətlər

Şəxsi dəyərlər dəsti λ 1 ,..., λ N matrislər Açağırdı spektr A.

Spektr müxtəlif xüsusiyyətlərə malikdir. Xüsusilə

det( A) = λ 1×...×λ N, Sp( A) = λ 1 +...+λ N.

İxtiyari matrisin özəl dəyərləri mürəkkəb ədədlər ola bilər, lakin əgər matris simmetrik olarsa ( A t = A), onda onun xüsusi dəyərləri realdır.

2.8. Xüsusi vektorlar

Matrisdə A, ölçü ( N× N) -dən böyük ola bilməz N hər biri öz dəyərinə uyğun gələn xüsusi vektorlar. Xüsusi vektoru təyin etmək v n homojen tənliklər sistemini həll etməlisiniz

(A − λ n I)v n = 0 .

Onun qeyri-trivial həlli var, çünki det( A-λ n I) = 0.

Misal üçün,

düyü. 22 Xüsusi vektorlar

Simmetrik matrisin məxsusi vektorları ortoqonaldır.